多特征融合和尺度变化估计的船舶跟踪方法

陈信强，凌 峻，齐 雷，杨勇生，周亚民

上海海事大学 物流科学与工程研究院，上海201306

近海水域的水上通航环境中，船舶值班人员需要及时有效获取他船的航行信息，并实时调整本船航行状态以规避船舶碰撞事故。智能船舶的发展为自动化地获取水上交通态势信息，优化船舶航线设计和预防海上交通事故提供了新思路。智能船舶可使用传统的船舶跟踪方法（如类GPS（Global Positioning System）的船舶自动识别系统、雷达等）获取水上通航信息[1-4]。已有的船舶跟踪方法将船舶视为质点，此类方法在分析宏观或中观水上交通态势变化时能获得较好的效果，但对微观水上交通态势感知（如近海区域的交通态势感知）研究的效果不理想。主要原因是船舶的长和宽等因素都会对水上交通态势判断产生不可忽略的影响。基于闭路电视（Close Circuit Television，CCTV）监控视频的船舶数据可提供三维船舶跟踪数据，为近海水域的水上交通态势感知提供更为有效的通航信息。

不同于车辆跟踪等常见视觉跟踪任务，基于水上交通图像的船舶跟踪任务中，图像背景（主要是海浪）为非刚性物体运动模式，其随着船舶运动状态的变化而呈现出无规则、非刚性的成像规律。此外，不同海况、天气、光照条件等因素也会对船舶成像造成干扰，弱化船舶的可视化特征，为船舶跟踪提出了额外的挑战。为应对船舶跟踪挑战，滕飞等人[5]利用先跟踪再学习的检测框架，构建特征约束方程校验像素（pixel）的运动状态，并通过求解像素与特征方法相关系数的关系，获得了稳定的、可靠的短时船舶跟踪效果。刘德华[6]针对复杂内河通航环境下的船舶跟踪难题，构建了一种改进的连续自适应均值偏移（Continuously adaptive mean-shift，Camshift）跟踪算法，通过优化适应度函数，增加颜色概率相似性计算过程，以获得较好的船舶跟踪结果。张云飞等人[7]利用孪生网络和区域推荐网络的方法构建了一种可实现船舶实时跟踪的框架。Chen 等人[8]针对遮挡等典型水上交通场景下的船舶跟踪挑战展开了相关研究。部分学者基于水天线检测、深度学习和相关滤波等方法，构建可实时性、鲁棒性地获得船舶跟踪效果的框架[9-14]。

综上所述，已有研究主要集中在单目标船舶跟踪任务，涉及水上通航态势感知任务的多船舶跟踪研究较少，针对不同海况干扰下的多船舶跟踪的相关研究更少[15]。为此，本研究提出一种基于多特征融合和尺度滤波的船舶跟踪框架，并将其应用于不同海事交通场景下多目标船舶跟踪任务，以验证提出算法的有效性和可行性。

1 基于多维度特征融合机制和尺度变化估计的多目标船舶跟踪

针对多目标船舶跟踪任务，利用相关滤波算法提取图像中船舶方向梯度直方图（Histogram of Oriented Gradients，HOG）特征，并使用该滤波器来判断船舶在下一帧图像的位置。在船舶尺度估计过程中，根据平移滤波器得到当前帧目标船舶的位置，并利用尺度滤波器获取不同尺度的候选船舶目标的最大响应，以得到该船舶在当前图像帧的尺度。在此基础上，算法以循环迭代的方式对当前图像帧的其他船舶目标执行类似操作，以获取当前图像帧中所有目标船舶的位置。对当前图像所有目标船舶完成遍历循环跟踪后，算法对后续图像序列的目标船舶均执行类似操作，以获得海事视频序列中多目标船舶的位置集。为简单起见，后续章节以单一目标船舶跟踪为例，对提出的多目标船舶跟踪方法进行阐述，算法流程图如图1所示。

图1 提出的多目标船舶跟踪方法的流程图

1.1 基于一维特征的船舶位置估计

对于给定的船舶图像帧，提出的船舶跟踪方法从训练图像中选择包含目标船舶的一组灰度图像块f1,f2,…,ft以提取船舶HOG 特征，并利用高斯函数对其进行训练学习。假定高斯函数的滤波响应输出为g1,g2,…,gt，则船舶跟踪结果的最优解应该满足如下关系：

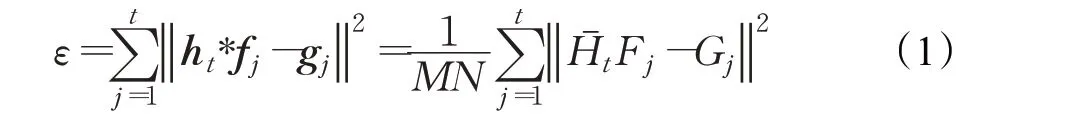
其中，变量ht、fj、gj均为M×N矩阵，“*”表示循环操作，参数Ht、Fj和Gj为ht、fj、gj的离散傅里叶变换函数，为共轭复数。

式（1）的最小值可通过下式获得：

当高斯函数作用于图像块fj的极值时，理想的相关滤波输出和分别为Gj和Fj的共轭复数，实际的求解过程中，更新了目标船舶的跟踪模板后，再分别对Ht的分子At和分母Bt进行更新。

1.2 基于多维特征的船舶位置估计

为获得更好的船舶跟踪效果，基于前述的单维特征的相关滤波船舶跟踪方法，构建基于多维特征的船舶跟踪机制。给定船舶图像序列，用符号f表示从该帧提取的船舶样本图像，f l为船舶特征维度lϵ{1,2,…,d}对应的特征，参数d为特征维度序号。船舶位置估计（船舶跟踪）问题转换为寻找相关滤波函数h的最优解，其中hl为特征维度l的代价函数，该问题转换为求式（3）的最优值：

其中，参数g为滤波器在当前图像帧中循环迭代中的最大响应（即目标船舶在当前图像帧的位置），参数λ为正则化参数。

针对式（3），其最优解如下所示：

Fl为f l的离散傅里叶变换形式，Fk为不同的船舶样本特征维度的离散傅里叶表示，为Fk的共轭复数形式。当船舶训练样本与滤波结果差异最小时，可得到最佳的滤波结果（式（4）的最优解）。针对任一图像像素构建d×d线性系统方程，即将式（4）变换为式（5）和（6）：

其中，参数η为学习率，为At的傅里叶变换形式（该规则适用于

根据式（7），判定当前图像中矩形区域z被视为目标区域的分值y（即置信度）为：

利用式（5）和（6）进行滤波器的更新，并利用式（7）进行相关分值y的更新，获得图像中目标的位置估计，即分值最大的响应被视为目标船舶在当前帧的位置。

1.3 船舶尺度估计

为了实现目标船舶的尺度估计，构建了一种三维尺度空间滤波器，滤波器的尺寸是M×N×S，其中M和N分别是滤波器的宽和高，而S是滤波器的尺度数量。针对给定的船舶区域，首先计算一个特征金字塔。输入的训练船舶样本f中心即为重构的特征金字塔，利用三维高斯函数获得训练样本在当前输入图片的最大响应，根据式（5）和式（6）更新船舶尺度信息，式（7）的分值为最大时，认为当前获得的船舶尺度参数为尺度空间滤波器输出的尺度信息，可视为目标船舶在当前图像帧的尺度。

2 实验结果

2.1 评价指标

为了评价船舶跟踪算法的性能，需要量化对比本研究提出的船舶跟踪算法得到的船舶位置与手动标定的船舶位置（即船舶在图像序列中的真实位置）误差，本文利用中心点平均跟踪误差（Average Center Location Error，Ce）、均方根误差（Root Mean Square Error，RMSE）、平均绝对误差（Mean Absolute Deviation，MAD）和均方误差（Mean Square Error，MSE）这4 个指标，计算公式如下所示：

xt和yt为算法跟踪得到的船舶位置（x坐标和y坐标），而xg和yg为船舶真实坐标位置，m是图像帧的序号。

2.2 实验分析

本文研究首先测试了算法在正常海况下多船舶跟踪的性能。图2 给出了正常海况下的原始船舶图像序列及本文算法得到的多目标船跟踪结果图。从图2（b）可看出，待跟踪的目标船舶在驶离相机监控区域的过程中，其成像尺度呈现了逐渐变小的趋势。当目标船舶相互之间没有遮挡，且目标船舶没有受到明显海况的干扰时，本文提出的船舶跟踪算法能较好的判断每帧图像中的船舶位置和船舶尺度，并得到比较满意的船舶跟踪结果。此外，当目标船舶在相邻的航道行驶（即船舶成像区域比较接近），且被跟踪的船舶外观特征比较接近时，本文研究提出的算法依然能较好地获得船舶位置。主要原因是提出的船舶跟踪算法通过循环迭代的方式寻找训练样本与当前图像帧的最大响应。当目标船舶的图像邻域出现了干扰像素（如图2（b）的船舶3 和船舶4），但不同船舶间的外形（如轮廓、边缘等）差异性仍然会被本研究提出的算法进行累积放大，从而有效抑制船舶跟踪的干扰。

图2 正常海况下的典型图片帧序列及跟踪结果

为了进一步验证算法的性能，分别给出案例1 的4艘目标船舶的跟踪误差曲线分布图。图3（a）、（b）和（c）显示本研究提出的船舶跟踪算法在每一帧的船舶跟踪误差均不超过5个像素，这说明图像序列中船舶1、船舶2 和船舶3 跟踪得到的结果与船舶真实位置相差不大。图3（d）最大的跟踪误差达到10 个像素，说明提出的算法在该船舶的跟踪精度略低于其他3 个子图。相比于其他的3 个船舶，船舶4 的外观特征与水面特征比较接近，因此会误导跟踪算法提取额外的水面背景信息以更好地确定船舶位置。根据目标跟踪精度准则，如果跟踪误差在20 个像素以内，则说明跟踪算法得到的效果近似于真实值。基于此，可认为提出的船舶跟踪方法在海况正常的情况下能有效地实现多目标船舶跟踪的目的。

图3 正常海况下船舶跟踪误差分布曲线

为了进一步测试算法的有效性，将提出的船舶跟踪算法分别应用于阴天和海浪干扰条件下的多船舶跟踪图像序列（见图4），由于篇幅限制，这里不给出典型图像帧的船舶跟踪结果，仅给出不同跟踪场景下的误差分布。表1显示3种典型船舶跟踪场景下中心点的平均跟踪误差均比较小，其中海浪干扰场景下的船舶跟踪误差2.52像素，比正常海况和阴天条件下的船舶跟踪误差值大概低10%（分别为3.32像素和3.09像素），这主要是因为海浪的成像与待跟踪的目标船舶成像差异较大，因此对船舶跟踪的干扰相对较小，而另外两种跟踪场景下的船舶与场景相似度更高，因此Ce的值比第3 种场景的值更大。类似的，海浪干扰下的RMSE指标值同样小于其他两种情况。

图4 不同海况干扰下的典型船舶跟踪图像

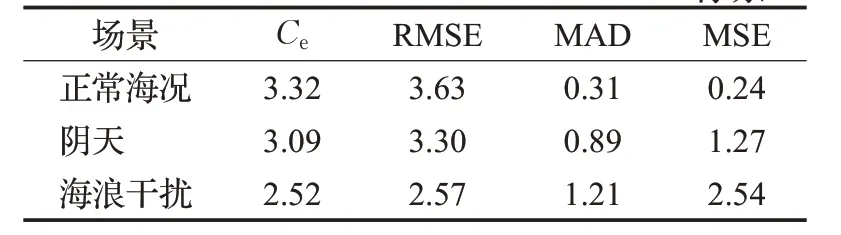
表1 本文研究构建的船舶跟踪方法的跟踪精度 像素

表1 的MAD 和MSE 指标反映了不同船舶跟踪案例下误差的分布程度。正常海况下的MAD 和MSE 值分别为0.31 像素和0.24 像素，而海浪干扰条件下MAD和MSE 值为1.21 像素和2.54 像素，至少比正常海况下MAD和MSE值大4倍。这说明海浪对船舶跟踪算法呈现出比较明显的瞬间干扰特性。在部分海浪干扰比较严重的图像帧中，船舶跟踪算法的跟踪误差会比较大（这与图3（d）部分跟踪误差值接近10 个像素的吻合），而海浪遮挡不明显的情况下，其跟踪误差又明显小于其他两个跟踪场景。

为了比较算法的跟踪效果，将中值流（median flow）跟踪算法和多示例学习（multiple instance learning）跟踪算法在上述3个场景下分别进行跟踪测试并统计了误差分布（如表2和表3所示）。这两种算法阴天海况时跟踪误差最大。中值流算法在处理海浪干扰时效果优于处理其他场景，多示例学习方法在正常海况和海浪干扰时跟踪误差未见明显区别。在正常海况、阴天和海浪干扰三种典型交通场景下，本文研究提出的船舶跟踪算法的各项误差指标均明显低于其他两种跟踪算法，说明了提出的算法具有更高的船舶跟踪精度。

表2 中值流跟踪方法的船舶跟踪精度 像素

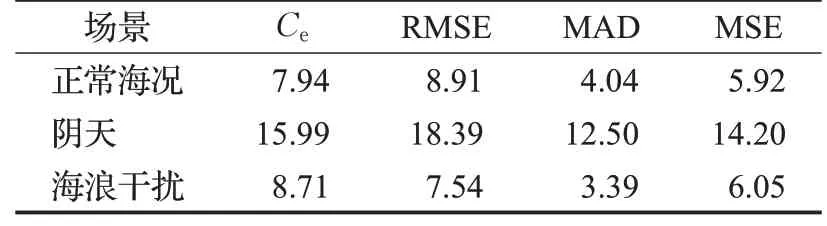
表3 多示例学习跟踪方法的船舶跟踪精度 像素

3 结论

船舶跟踪是获取水上交通态势感知信息的重要途径，也是智能船舶智能航行需要解决的关键问题。本文研究针对海上交通图像序列中多目标船舶跟踪挑战，构建了一种基于多维度特征和尺度变化估计的多目标船舶跟踪方法。该方法首先利用位置滤波器学习训练样本的船舶特征，并针对输入的图像序列获取最大响应以判断当前图像的船舶位置，在此基础上，构建特征金字塔对船舶的尺度进行再次更新，最终获得多目标船舶在图像序列中的位置。实验结果表明，提出的多目标船舶跟踪算法在正常海况、阴天和海浪干扰较大等典型海事交通场景下均能获得较好的效果。测试船舶长时间被遮挡、船舶无规律的驶入/驶出相机监控范围下算法的鲁棒性测试，是未来需要开展的研究工作。