结合MLR和ARIMA模型的时空建模及预测

李 莎，林 晖

1.湖北第二师范学院 物理与机电工程学院，武汉430205

2.武汉数字工程研究所，武汉430205

随着全球气候变暖，气候变化已成为全球热点关注的问题之一。中国气候变化趋势与全球变化基本保持一致，1951—2009年中国全国年平均气温上升1.38 ℃，变暖速率达到0.23 ℃/10a[1]。近年来，国内外有大量关于气候变化分析和预测方面的研究。比如Hengl等[2]运用回归克里金法（regression-kriging）对日均气温进行时空预测，其中回归处理过程使用观测站点经纬度、离海距离、海拔、时间、MODIS 地表气温图像等信息对气温进行回归模拟。Meyer等[3]分别运用线性回归法与随机森林（RF）、广义增强回归模型（GBM）、Cubist[4]等3种机器学习算法，对南极洲地区的日均气温进行空间分辨率为1 km 的插值预测。Kilibarda 等[4]针对全球陆地日均气温进行分辨率为1 km 的时空插值研究，其中运用多元线性回归模型（MLR）通过站点纬度和测量时间等协变量模拟气温的变化趋势。Li 等[5]将时空MLR 与克里金模型结合对东北三省月均气温进行插值研究，研究结果表明引入MLR 的插值精度要好于普通时空克里金。朱文博和朱连奇[1]运用AUNSPLINF方法对甘肃省50年的月均气温进行插值处理，获得空间分布图并进行趋势特征分析。李均力等[6]以阿牙克库木湖为研究对象，利用Corona、Landsat、HJ1A/1B 等形成的长时间序列遥感数据，分析其50年的年度和季节性变化特征，并结合降水、气温等数据分析与气候变化的响应。任婧宇等[7]采用距平、Mann-Kendall 趋势检验和Sen’s 斜率估计方法分析在黄土高原地区未来时期四季气候变化的时空分布特征。

ARIMA（差分自回归移动平均）模型，即Box-Jenkins法，是一种常见的时间序列预测分析方法，广泛应用于医疗卫生预测[8-9]、国民宏观经济控制[10]、气象预测[11]、交通运输预测分析[12-13]等各个领域。传统的气象数据插值预测多为时间域的预测或空间域的插值（比如常见的克里金插值法[14-15]）。但是气象变量具有典型的时空分布特点，比如地表气温的变化，不仅受时间的影响，还与气象站点的地理位置、海拔高度等多种因素有关，因此，为了更好地拟合气象变化规律，近年来时空多元线性回归（MLR）模型被广泛应用于时空数据相关结构的建模和分析。比如在气象和环境等领域，时空MLR 模型与克里金插值法相结合称作时空回归克里金法，它被认为是一种有效的时空插值方法而常被使用[5，16]。相比于普通克里金法，回归克里金法可以大幅度提高解释变量变化趋势的比例[2]。此方法中，回归建模实际上与克里金法是分离的。引入回归建模，通过多个已知协变量模拟被研究变量的全局变化趋势（空间变化趋势、时间变化趋势或者时空变化趋势），继而去除全局趋势以保证数据的平稳性[17-18]。为了进一步描述气温与其他变量的相关性，提高时空预测精度，本文构建了一个基于ARIMA模型和时空MLR 模型的预测方法：（1）通过时空MLR 建模，获得地表气温关于时间、空间位置以及海拔等因素的时空变化趋势，并分析和评价各因素对气温的影响程度；（2）运用ARIMA 模型对MLR 拟合残差进行时序拟合及预测，绘制预测曲线和误差分布图，并评价预测精度。

1 算法描述

1.1 时空MLR模型

在回归分析中，如果有两个或两个以上的自变量，则称为多元回归，而如果自变量既包含空间变量又包含时间变量，则是时空多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。气温就是一种常见的时空变量，同时用其空间和时间的分布特征来进行预测，理论上应该会具有更高的预测精度。

假设数据样本为(Yi,X1i,…,Xki)，i=1,2,…,n，那么其多元回归总体回归函数为：

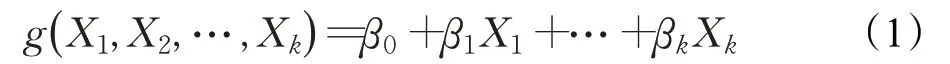
模型拟合的优劣可通过判断残差的正态性、独立性等来诊断，而模型中自变量的选取常采用逐步回归法和全子集回归法[19]。

1.2 ARIMA模型

常用的时间序列模型有自回归模型AR(p)、移动平均模型MA(q)、自回归移动平均模型ARMA(p,q)以及差分自回归移动平均模型ARIMA(p,d,q)。其中，前3种常用于分析平稳时间序列，而ARIMA通过差分可以用于处理非平稳时间序列，因此ARIMA 更具有广泛性和通用性。非平稳时间序列是指包含趋势性、季节性或周期性等特性的序列，它可能只含有其中的一种成分，也可能是几种成分的组合[20]，且平稳时间序列可以看作是非平稳序列的一种特例。在消去局部水平或者趋势之后，非平稳时间序列显示出一定的同质性，经过差分处理后可以转换为平稳时间序列，这样的时间序列称为齐次非平稳时间序列，其中差分的次数就是齐次的阶。

假设Yt是一个时间序列，那么其ARIMA(p,d,q)模型可表示为：

其中，p为自回归阶数，d为使之成为平稳序列所做的差分次数（阶数），q为移动平均阶数，L是滞后算子，ϕi为自回归部分的系数，θi为移动平均部分的系数，εi为残差，是一个零均值白噪声序列。

建立ARIMA模型的步骤通常如下：

（1）验证序列的平稳性。

（2）拟合模型，确定模型参数(p,d,q)。

（3）模型评价。一般来说，若模型合适，则模型的残差应满足独立正态分布；若不满足，则返回至第（2）步重新确定模型参数。

（4）用模型进行预测。

2 实验数据

本文实验数据由中国气象科学数据共享服务网提供，该数据包含若干气象要素：风速、气温和降水。选取1972 年1 月至2008 年12 月辽宁省月均气温数据为研究对象，应用ARIMA 和MLR 模型进行时空分析和预测。数据共涉及444 个月，27 个气象观测站点，站点分布如图1 所示，其中4 个站点（新民、草河口、皮口、长海）的部分气温数据缺失，缺失情况如图2 所示。存在缺失数据的站点，其站点的地理位置以及有效采样的气温数据依然能够为样本的建模分析提供有效的时空分布信息，因此实验中没有删除。实验以1972—2005年共408 个月数据进行建模，对2006—2008 年各月各站点进行预测。

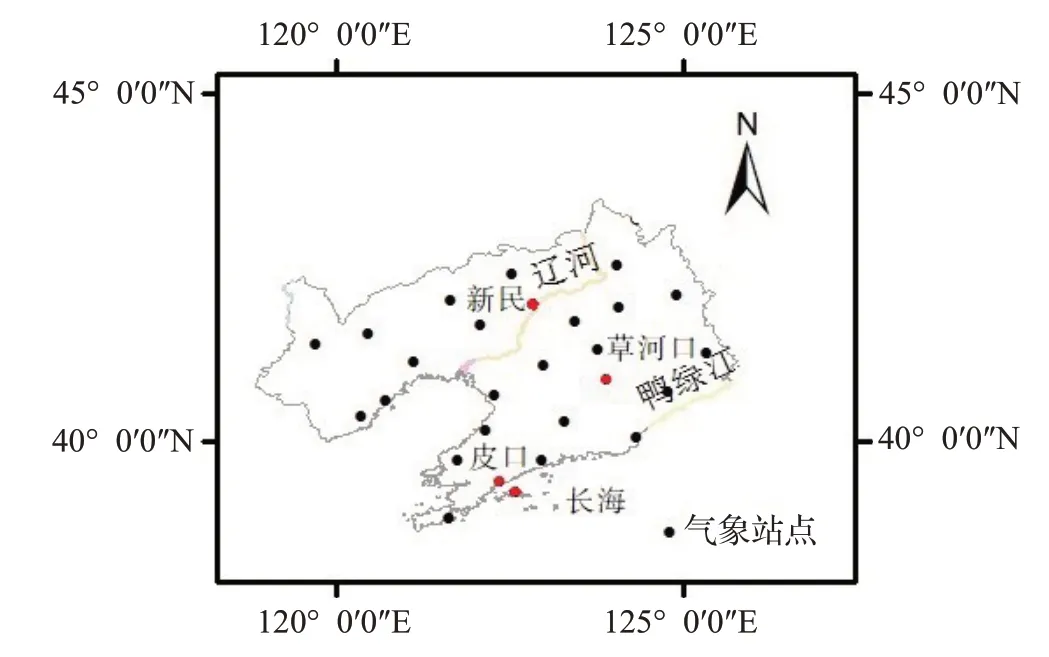
图1 气象观测站点分布图

图2 数据缺失站点的月均气温

3 实验分析

3.1 时序分解

气温的时空分布并不平稳，尤其是时间分布上具有显著的季节变化特点[21]（如图3 所示）。ARIMA 模型虽然可以通过差分处理将非平稳时间序列转换为平稳时间序列，但是为了优化模型拟合效果，通常会预处理其中显著影响平稳的成分。而一个含有周期（季节）变化的时空变量通常可以分解为三个部分：时空趋势项、时空季节项和时空随机项。

图3 沈阳站点月均气温时序分解

若将辽宁省各站点的月均气温观测值定义为时空变量MAT={MAT(s,t)|s∈S,t∈T}，(s,t) 为时空域(S,T)内的某一点，则：

其中，Sea(s,t)为时空季节项，Tr(s,t)为时空趋势项，R(s,t)为时空随机项。对应于实验数据的时间范围，1972 年1 月记为t=1，2006 年1 月记为t=409。由于气温的变化周期为12 个月，则同一个站点的气温在不同年度相同月份的季节项一致，即：

式中的季节项Sea可以通过对每个站点时序分解进行逐一提取（图3所示为沈阳站点月均气温的时序分解），而去除Sea之后的数据记为去季节项数据SRD。

3.2 时空趋势拟合

除了显著的季节变化之外，月均气温还与站点的地理位置、所处的海拔高度以及一年当中所处月份有关，这种变化趋势对应的就是式（5）中的时空趋势项Tr(s,t)，它可以通过MLR模型进行拟合。在去季节项数据的基础上，如果将Tr进行提取分离，理论上剩下的数据应该是平稳的随机项R(s,t)。

时空趋势拟合可能涉及站点的东西坐标x，南北坐标y，海拔高度d，时间坐标m等变量，本文通过全子集回归法来确定变量的选择。图4所示，基于调整R平方（adjr2），同时含有截距项（INT）、d、y、x和m变量时，adjr2 达到最大值0.38，即此时的MLR 模型最佳，具体参数见表1。图5 所示，站点的南北坐标对SRD 的影响最大（权重达到45.5%左右），其次是东西坐标（权重约24.7%）。这说明在消除季节性影响因素之后，气温受地理位置的影响较大。图6所示，MLR拟合误差的核密度曲线与正态曲线基本一致，这说明误差很好的服从了正态分布，模型拟合效果良好。

图4 SRD全子集回归图

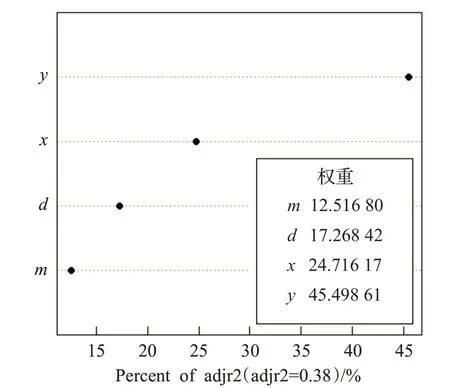
图5 MLR模型各变量相对权重点图

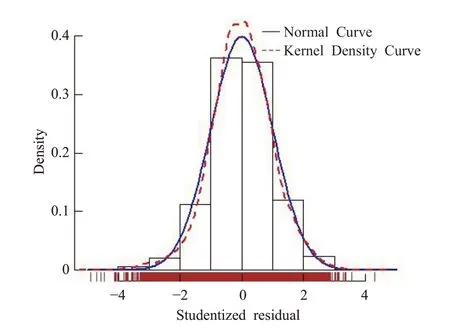
图6 MLR模型学生化残差分布图

表1 时空MLR模型参数表

3.3 ARIMA建模

进行ARIMA 预测之前，通常要对时间序列进行平稳性检验。实验依次对每个站点的R(s,t)时间序列进行ADF 检验，均是平稳的。以沈阳站点为例，其自相关图和偏相关图如图7 所示，可见该站点R(s,t)是平稳的，基于AIC 信息准则，其ARIMA 模型参数分别为p=2，d=0，q=0，连同其他站点R(s,t)时间序列的ARIMA模型见表2。表2中显示有多个站点的ARIMA模型参数相同，比如开原、清原等14 个站点的模型都为ARIMA（2，0，0），彰武等3 个站点的模型都为ARIMA（1，0，3），章党等4 个站点的模型都为ARIMA（1，0，0），阜新和黑山站的模型为ARIMA（0，0，3）。由于各模型的自回归系数（AR）、移动平均系数（MA）、截距（INT）等不同，所以各站点的ARIMA 模型实际互不相同，表3 是部分站点模型为ARIMA（2，0，0）的系数列表。

表2 各站点随机项时间序列ARIMA模型

表3 ARIMA（2，0，0）模型系数

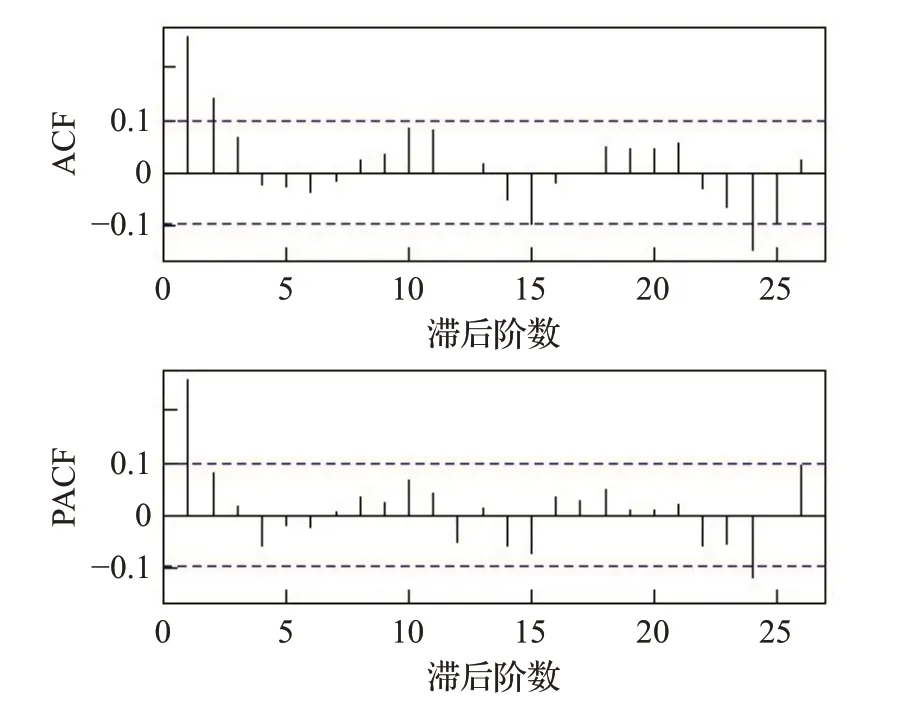
图7 沈阳站随机项ACF图和PACF图

3.4 预测结果分析

以27个站点前408个月的月均气温数据为训练集，依次进行时序分解、MLR 拟合以及ARIMA 预测，将各阶段值按照式（5）合成各站点2006—2008 年共36 个月的月均气温预测值，并与同时段原观测值进行比较，预测结果如图8所示。图8（a）中观测值对预测值的点绝大多数落在或靠近y=x直线，且相关系数COR=0.993 4，非常接近于1；其时空预测误差近似服从正态分布，如图8（b）所示，约60%的误差在±1℃以内。进一步引入统计指标评价基于ARMIA 和MLR 模型的时空预测结果（如表4 所示），包括误差中位数（MED）、误差均值（ME）、误差绝对值均值（MAE）以及均方根（RMSE），其中RMSE按式（7）得到，式中MAT*(si,ti)为月均气温的预测值，N为预测点总数。

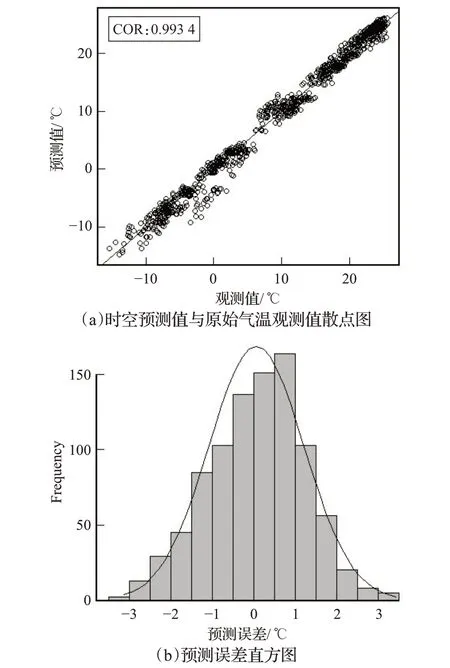
图8 时空预测整体结果

表4 时空预测统计指标

由表4 可见，2006—2008 年的整体预测误差MAE为0.927 7 ℃，RMSE 为1.151 0 ℃，说明时空预测整体效果良好。若按年份分别预测，MAE虽逐年增大，但相差不大，都在1 ℃以内，而RMSE 均略高于1 ℃。预测误差的空间分布以2006 年为例，图9 分别显示了2006年12 个月各站点的预测误差分布图，图中气泡大小对应该站点的误差绝对值大小，红色代表预测值小于观测值，绿色则相反。12个月中，大部分站点误差较小，2、3、5、6、8、9、11、12月共计8个月的MAE小于1 ℃，其中5、8、9、11月MAE甚至小于0.5 ℃。另外，2、4、6、7月各站点的月均气温预测值普遍大于实际观测值，而10 月的预测值普遍偏小，这主要是因为该月全省的月均气温较往年同期偏低或者偏高。如图10所示，2006年4月辽宁省全部站点（其中26、27 号站点观测值缺失）的月均气温值（红色）明显低于1972—2006 年4 月的月均气温平均值（蓝色），因此2006年4月的各站点气温预测值普遍偏高；而2006年10月的情况恰恰相反，由于该月全省各站点月均气温（红色）明显高于35 年的平均值（蓝色），导致当月的时空预测值整体偏低。由此可见，当某区域的气温出现较大幅度升降甚至出现极端天气时，将对气温预测增加难度。

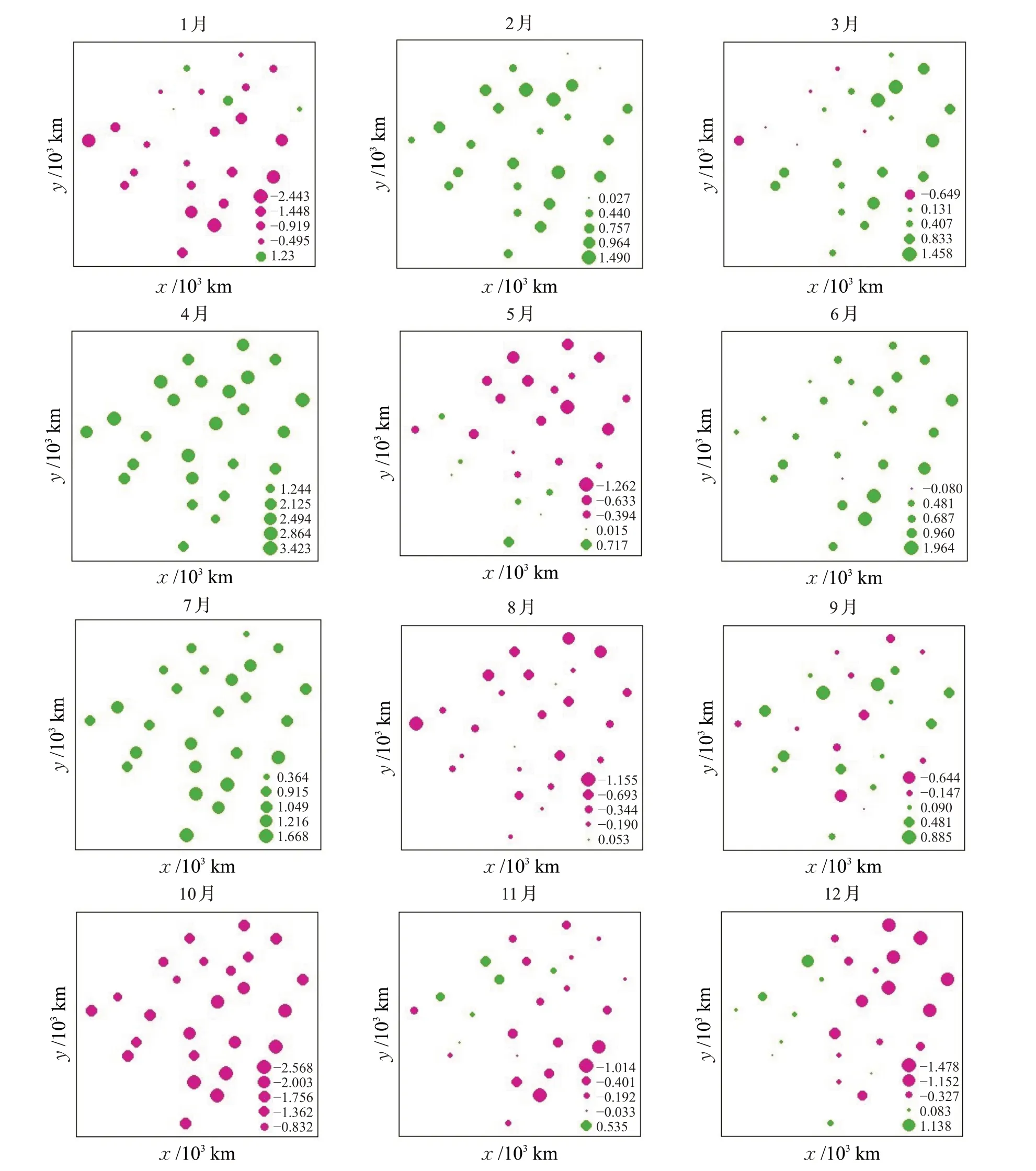
图9 2006年12个月各站点时空预测误差分布图

图10 气温观测值与对应气温均值对比图

4 结语

区域气温是时空分布的变量，就某一站点而言，气温是具有显著季节变化的时间序列，但就研究区域而言，它受地理位置、海拔高度等多种因素影响，且气温在时间和空间域的分布变化是交互的。本文将时空MLR模型和ARIMA模型应用于辽宁省的月均气温预测分析中，前者拟合气温的时空变化趋势，后者进行随机项预测，同时考虑了气温受空间、时间因素的影响。实验以1972 年至2005 年的数据为训练集，对2006 年各月进行整体预测，结果说明本文的方法能够实现较高精度的时空预测，同时针对少数预测误差较大的点，给出了进一步的原因分析。