Joint Computing and Communication Resource Allocation for Satellite Communication Networks with Edge Computing
Shanghong Zhang,Gaofeng Cui,3,*,Yating Long,Weidong Wang
1 School of Electronic Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,China
2 Key Laboratory of Universal Wireless Communications(Beijing University of Posts and Telecommunications),Beijing 100876,China
3 Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory,Hebei 050000,China
Abstract: Benefit from the enhanced onboard processing capacities and high-speed satellite-terrestrial links,satellite edge computing has been regarded as a promising technique to facilitate the execution of the computation-intensive applications for satellite communication networks (SCNs).By deploying edge computing servers in satellite and gateway stations,SCNs can achieve significant performance gains of the computing capacities at the expense of extending the dimensions and complexity of resource management.Therefore,in this paper,we investigate the joint computing and communication resource management problem for SCNs to minimize the execution latency of the computation-intensive applications,while two different satellite edge computing scenarios and local execution are considered.Furthermore,the joint computing and communication resource allocation problem for the computation-intensive services is formulated as a mixed-integer programming problem.A game-theoretic and many-to-one matching theorybased scheme (JCCRA-GM) is proposed to achieve an approximate optimal solution.Numerical results show that the proposed method with low complexity can achieve almost the same weight-sum latency as the Brute-force method.
Keywords: satellite communication networks; edge computing;resource allocation;matching theory
I.INTRODUCTION
As stated in the report of International Telecommunication Union(ITU),satellite communication networks will provide high-speed Internet access services for billions of users,especially for those in rural areas and isolated islands [1].Benefit from the broad coverage and flexible deployment,SCNs have gained lots of attention in several scenarios,such as remote sensing,Internet of Things,vehicle to vehicle communication in remote areas and so on [2].In the above scenarios,with user terminals’ (UTs) increasing demands for higher quality of services (QoS),UTs with limited computation and storage capacities will be hardpressed to provide high reliability and low latency services for computation-intensive applications.In this way,task offloading can be a feasible option [3].Although a cloud-enabled framework has been proposed for SCNs that allows UTs to offload the computationintensive applications to the powerful cloud server,the far propagation distance between UTs and the cloud server will make UTs suffer from large delay [4].Besides,one gateway station may serve for multiple satellites,the feeder link between satellites and gateway station is constrained [5],satellites may not be able to deliver the tasks to the cloud center in time.As an alternative approach,mobile edge computing(MEC) with proximate access is generally regarded as an efficient way to transfer the computation and storage resource from cloud servers to local servers,which can significantly improve the QoS of UTs with computation-intensive applications[6].
In the past years,under academia and industry’s enduring research work,the fusion of MEC and wireless communications has been well investigated[7].However,the research on the integration of SCNs and MEC is few [8].Due to the limited payload,storage and communication capacity,traditional satellites generally act as relays with no or few onboard processing capacities[9,10].Fortunately,with the rapid development of satellite manufacturing and deployment technologies,such as re-configurable onboard processing using FPGA [11]and Ka-band phased array antenna[12],nowadays,satellites can provide low-cost,lowlatency,broad coverage and high-throughput services for UTs [13,14].In the flight of this,edge computing techniques can be introduced into SCNs to further enhance the QoS of SCNs,especially for UTs with computation-intensive applications[15,16].
The introduction of computing resource extends the dimension and complexity of SCNs’ resource management[17].According to 3GPP TR38.811,UTs of SCNs can access core networks through service link and feeder link as shown in figure 1,a service link refers to the radio link between the UTs and satellite,and a feeder link is the radio link between the gateway and satellite [18].Under this framework,edge computing servers can be deployed in satellites and gateways[19].When the edge computing servers are deployed in the satellites,the traffic for the feeder link and backhaul link is reduced.However,the computing capacity and energy of satellites are limited,offloading the computation-intensive applications to the satellites may further aggravate the energy consumption and hardware complexity of the satellites.There will be a tradeoff between the QoS of SCNs and the cost of the satellites.If the edge computing servers are deployed in the gateways,sufficient energy supplies and convenient maintenance will significantly improve the computing capacities of SCNs by remote terrestrial offloading (RTO) at a low cost.At the same time,it can reduce the traffic of the backhaul link.
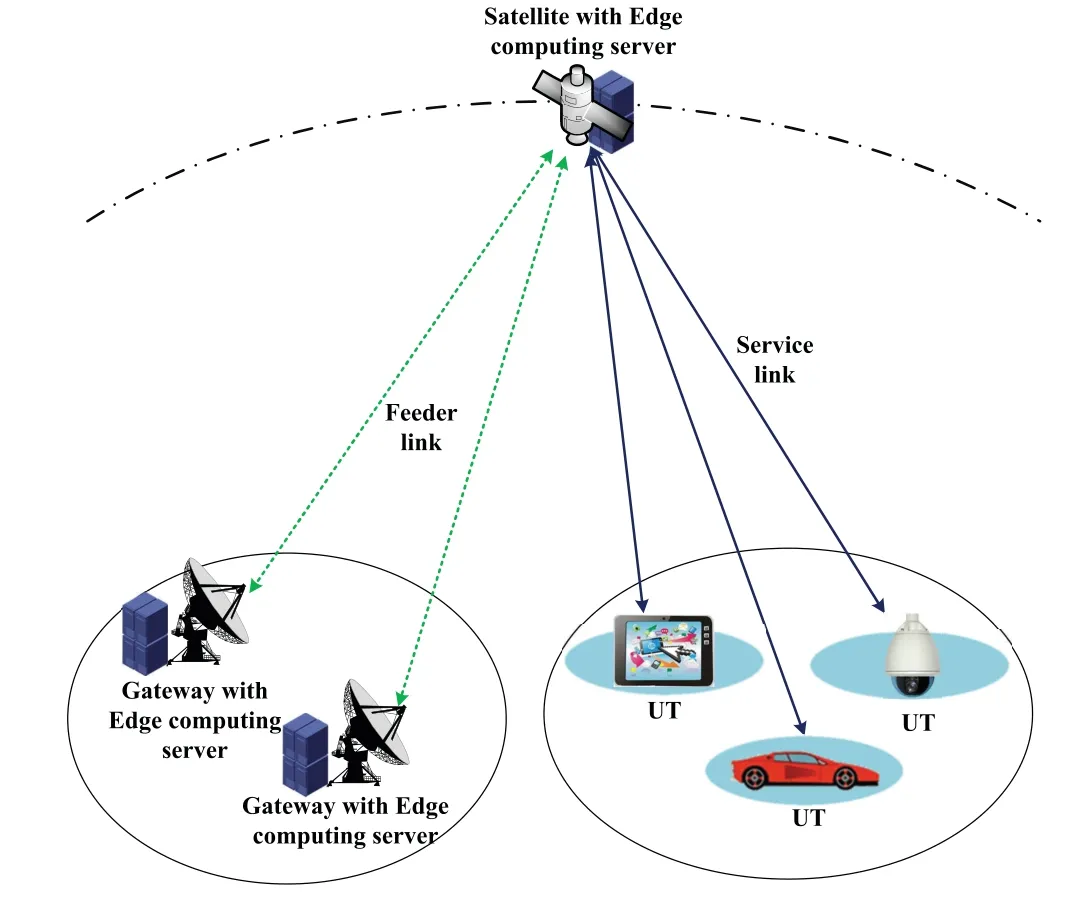
Figure 1.Scenario of SCNs with edge computing servers.
Even though SCNs can benefit from the deployment of the edge computing serves in the gateways,the intensely competitive backhaul resource and sparsely distributed gateways will lead to an intermittent feeder link[20].In this way,satellite edge computing scenarios can be classified into two categories.One is SCNs with edge computing servers in the satellites and there is no feeder link and RTO.The other is SCNs with edge computing servers both in the satellites and gateways,UTs can offload computing-intensive applications to the satellites or gateways.Besides of edge computing servers,UTs also have limited computing capacity [21].From the perspectives of resource management,SCNs with edge computing servers are the space-ground heterogeneous multi-layer networks with unevenly distributed multi-dimensional limited resource.Therefore,how to efficiently allocate the unevenly distributed and multi-dimensional resource of SCNs to guarantee the QoS of the computationintensive applications is the key issue addressed in this paper.
In this paper,we investigate the joint computing and communication resource allocation problem for multiple UTs with the computation-intensive applications of SCNs with edge computing servers.Meanwhile,the unevenly distributed multi-dimensional constrained resource,multiple UTs with local execution and different satellite edge computing scenarios are considered.And we formulate the resource management process as a mixed-integer programming problem,where the optimization objective is to minimize the weighted sum of latency of the computation-intensive applications.The main contributions are summarized as follows.
1.We establish the system model of the joint computing and communication resource allocation problem for SCNs with edge computing servers.Fully considering the characteristics of SCNs,two scenarios where there are multiple gateways with edge computing servers or no feeder link are investigated.In these scenarios,multiple UTs are served by satellite and can execute the computation-intensive applications locally or offload to edge computing servers for execution.
2.Taking the weighted sum-latency as an optimization objective,we formulate the joint computing and communication resource allocation problem as a mixed-integer programming problem.In order to solve the NP-hard problem,we decompose the problem into three sub-problems: a)Whether to offload the tasks? b) Where to offload the tasks? c) How to allocate the constrained communication and computing resource of the satellites and gateways for multiple UTs? Specially,for the scenario where there is no feeder link for the satellite,UTs can only offload their tasks to the satellite.
3.To obtain the sub-optimal solution for SCNs,Karush-Kuhn-Tucker(KKT)conditions,a gametheoretic approach and many-to-one matching theory are adopted.Simulation results demonstrate that our scheme can achieve an approximate optimal solution,and the performance is very close to the method of Brute-force.Meanwhile,our scheme has a much higher computational efficiency than the Brute-force method.
The rest of this paper is organized as follows.The related work is analyzed in section II.Section III introduces the system model of SCNs with edge computing servers.Problem formulation and solutions for SCNs are presented in Section IV.Section V analyzes the proposed scheme.Numerical results are discussed in Section VI.Section VII draws the conclusions of the whole paper.Future research is given in Section VIII.
II.RELATED WORK
To improve the QoS of the satellite-terrestrial network,the framework of satellite MEC is proposed in[15]and different implementation schemes of satellite MEC are investigated.As stated in[13],compared to the cloud-enabled framework,the deployment of edge computing server in satellite and gateway can reduce the traffic of the feeder and backhaul link,and provide extensive computation capacity for UTs,which will reduce the transmission latency.Moreover,a dynamic network virtualization technique is adopted to integrate the resource of the satellite-terrestrial networks to achieve parallel task execution.The integration of Internet of Vehicles and SCNs is investigated in [22],where SCNs is introduced to provide seamless accessibility for vehicles and allow vehicles to offload their task through satellites.In[23],the satellite is introduced to assist flying unmanned aerial vehicles(UAVs)with edge computing servers to deliver the offloading tasks.However,in [22]and [23]satellites’role is a relay and the task would be finally offloaded to other edge computing servers or the cloud server.A game-theoretic based scheme to find the best offloading strategy for SCNs with edge computing is proposed in [24],but the communication resource allocation and edge computing servers at gateways are not considered.Authors in[25]investigate the user association and offloading decision problems for satelliteaerial integrated computing networks,where users can offload their tasks to HAPs and satellite with edge computing servers.However,the computing and communication resource allocation in[25]is fixed.
Besides of the above-mentioned SCNs with edge computing,the cellular-based MEC networks or UAVenabled MEC networks have been well studied in recent years[46].However,most of the existing works concentrate on the single-layer or two-layer edge computing networks,in which UTs can only offload their tasks to a single base station or UAV with edge computing server[26–29].SCNs with edge computing in this paper are multi-layer edge computing networks,which are composed of three layers,i.e.,user layer,satellite layer and gateway station layer.Each UT has more alternative offloading decisions (local processing,satellite and gateway stations),which increases the complexity of offloading decision making.Moreover,different from the cellular-based MEC networks or UAV-enabled MEC networks,the propagation distance and the rain attenuation are generally omitted,the propagation delay,the rain attenuation and the antenna gain model for SCNs should be well considered.In addition to this,for the cellular-based MEC networks or UAV-enabled MEC networks,only the resource allocation in base station or UAV need to be considered.In this paper,the computing resource is unevenly distributed in UTs,satellite and multiple gateway stations,the communication resources of the feeder link and server link are also considered,how to effectively allocate the unevenly distributed and multidimensional resource of SCNs is a challenge.
There are also some papers that take multi-layer edge computing networks into account [30–32].Authors in[30]and[31]both propose a new framework of UAV-enabled MEC networks,where edge computing servers are deployed both in UAV and base station,UTs can offload their tasks to UAV or base station.However,only one UAV and one base station are considered in[30]and[31],whose scheme cannot be adopted in our SCNs with multiple gateway stations(edge servers)and local processing.Although authors in [32]consider the scenario of one UAV and multiple base stations with edge servers,user association and local processing is missing,and the data rate of the downlink link between UAV and base station for each UT is assumed to be fixed,which means that the communication resource allocation for downlink is not considered.
Taking the federated learning model into account,authors in [33]and [34]investigate the joint learning and communication resource allocation problem.However,this paper focuses on the model of data compression,whose objective is to process and transmit data within low latency,but the key point of federated learning together with resource allocation is to train the model with high accuracy and low latency.
In this paper,SCNs are multi-layer edge computing networks,satellites can access to multiple gateway stations to offload UTs’tasks.Which edge computing server should be offloaded to,how to allocate the limited computing and communicating resource of multiple edge computing servers all need to be addressed.Furthermore,the existing works generally focus on the one-way link resource optimization,which cannot guarantee the QoS of interactive services,such as remote sensing and control,this paper takes two-way link resource optimization into account.
III.SYSTEM MODEL
In this section,we first introduce the scenario of SCNs with edge computing servers and multiple UTs.Then,the communication model and computation model are presented.Finally,we analyze the response latency of each UT.
3.1 SCNs with Edge Computing
Given a typical scenario of SCNs with k UTs,one satellite and M satellite gateways,which is shown in figure 1.A set of UTs associated with the same satellite is denoted by K = {1,2,...,K}.For each UT k,its computing capacity can be represented by,the computation intensive applications of UTs k generate computing tasks,which need to be handled.For each scheduling period,only one of the tasks of each UT k,whose size is denoted as Nk,can be executed locally or offloaded to the edge computing server[35].Since the duration of each scheduling period is short,the topology is assumed to be fixed within one scheduling period.Moreover,only binary offloading is considered in this paper,the data generated by each UT can only be processed locally or by one of the edge computing servers.However,any edge computing server can handle the data generated by multiple UTs simultaneously.As a centralized scheduler the satellite will deal with the service requests of UTs and allocate computing and communication resource to them.The computing capacity for the satellite is Vsat.Furthermore,the available feeder links can be used to forward the data of UTs to the gateways.Since the gateways can be implemented with large reflective antennas and separated geographically one satellite can keep several feeder links with a set of gateways M = {1,2,...,M}through multiple beams,and the computing capacity of each gateway m is denoted by
Figure 2 shows the procedure of computing offloading for SCNs with edge computing servers.As shown in figure 2,when UTs have tasks that need to be handled,they will send a request to the associated satellite for computing offloading.Then,the associated satellite will allocate the computing and communication resource of the edge computing servers to each UTs according to the resource’s usage status of SCNs.Therefore,the task execution of each UT k can be divided into eight parts,local processing,UTs to satellite,satellite processing,satellite to gateways,gateway processing,gateways to satellite,satellite to UTsand propagation delay.Specially,for SCNs without RTO,,andare equal to 0.Moreover,because the delay of the signaling overhead is inevitable and keeps a constant,only the delay of task transmission and processing(from step 2 to step 7)shown in figure 2 and propagation delay are considered in this paper.Therefore,the response latency of UTs in this paper consists of three parts,the first part is the transmission latencythe second part is the processing latencyand,the third part is the propagation delay.And the weighted sumlatency is the weighted sum of the response latency of UTs.
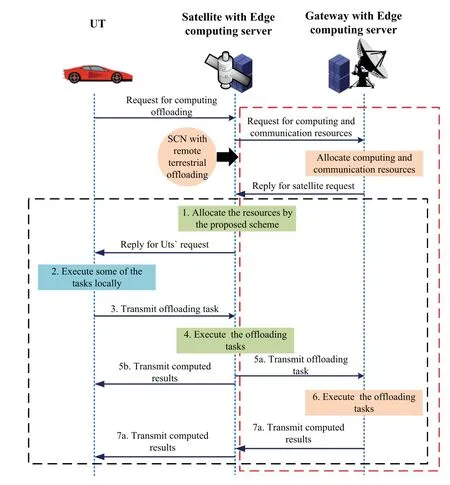
Figure 2.Procedure of computing offloading for SCNs with edge computing server.
3.1.1 Communication model
In this paper,the uplink and downlink communication resource will be allocated to UTs by the satellite,zkusandzksuis respectively the normalized uplink and downlink communication resource allocated to thekth UT,and the communication resource can be orthogonal sub-bands or time-frequency blocks[36,37].For instance,if SCNs adopt the OFDMA scheme for channel access,the allocated communication resource can be achieved with orthogonal sub-bands,and our proposed model can be extended into other types of communication resource.
Therefore,the transmission latencyTuskfrom UTs to satellite and the transmission latencyTsukfrom satellite to UTs for thekUT can be respectively given as,
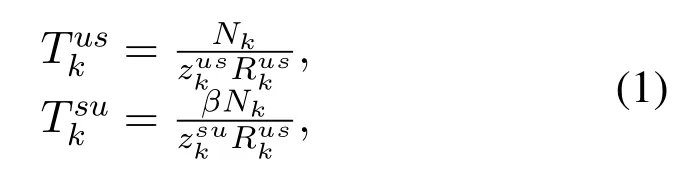
whereNkis the data bits that needs to be transmitted,βis the compression ratio of each task,this task model corresponds to many practical applications,such as the security monitoring systems,which will collect the video of surroundings and send the video to SCNs for analysis or compression,then SCNs will return the analysis or compression results to the security monitoring systems for the further monitoring or transmitting.Generally,the size of the analysis or compression results is smaller than the raw data,thus,this paper uses the compression ratioβto represent the changes in data size.AndRuskis the achievable data rate from UTkto satellite,which can be presented as,
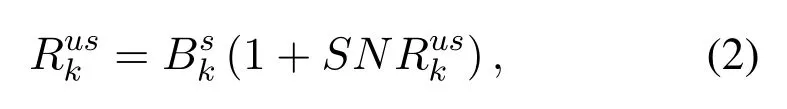
whereBskis the bandwidth,SNRuskis the SNR of the link from UT to satellite,which can be defined as,
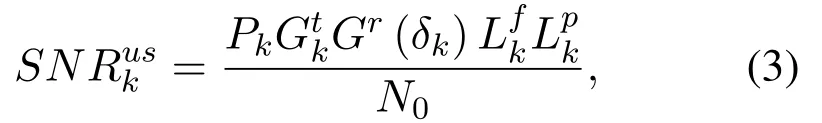
withPkbeing the transmission power of UTk,N0is the noise.AndGtkis the transmission power gain of UTk,Grk(δk)is the receiving antenna gain,which can be presented as,
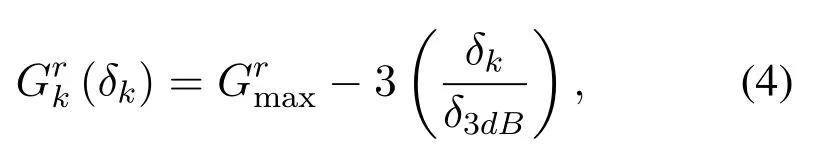
whereδkis the corresponding off-axis angle with respect to maximum radiation of satellite’s beam,and the value ofδkis related to the relative position between user and satellite.In this way,UTs which are close to the center of the beam will obtain larger antenna gain.Grmaxandδ3dBis the maximum and the half-power angle receiving antenna gain of the satellite,respectively.Lfkis the free space loss,which can be obtained by,
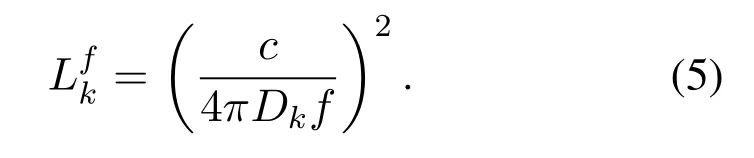
Andcis the speed of light,Dkis the propagation distance between user and satellite,andfis the communications center frequency.Lpkis rain attenuation,which is formulated from frequency,elevation angle,altitude above sea level,and rainfall intensity,can be presented as[38],
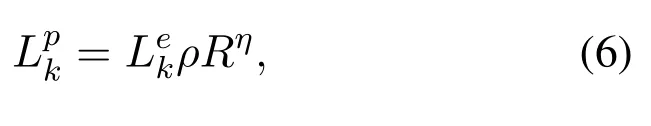
whereLekis the equivalent effective slant-path length,andLekis constant when the relative position between user and satellite is fixed,which can be obtained from the report of ITU-R P.618-12.AndRis rainfall intensity,ρandηis the coefficients,which is related to the frequencyfand can be obtained from the report of ITU-R P.838.In the same way,the achievable data rateRsukfrom satellite to UTkcan be obtained.
The achievable data rateRsgmfrom satellite to gateway stationmcan be defined as,
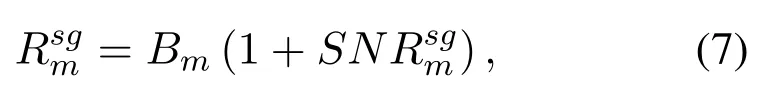
andSNRsgmis the SNR of the link from satellite to gateway stationm,which can be defined as,
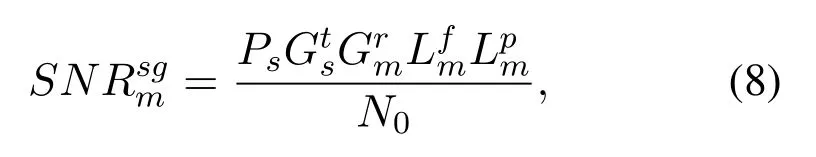
wherePsis the transmission power of satellite.GtsandGrmis the transmission and receiving power gain,respectively.Lfmis the free space loss,andLpmis rain attenuation,which can be obtained as formulation(6).Similarly,the achievable data rateRgsmfrom gatewaymto satellite can be obtained.
And the latency brought by the transmission from satellite to gatewaysTksgand gateways to satelliteTkgsfor UTkcan be expressed respectively as,
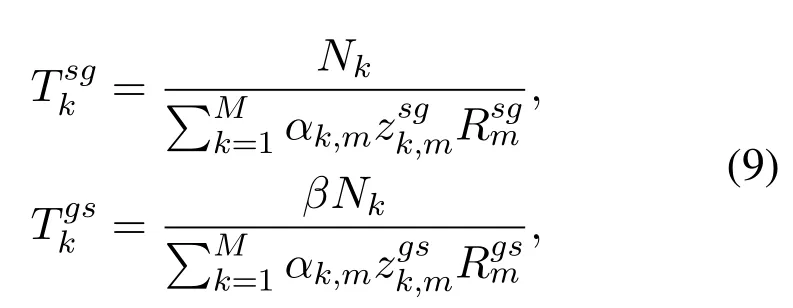
whereis the normalized downlink communication resource allocated to thekth UT from the satellite to themth gateway,andis the normalized uplink communication resource allocated to thekth UT from themth gateway to the satellite.αk,mis the association indicator of thekth UT,αk,m=represents the task of the UTkthat will be executed in the gatewaym,otherwiseαk,m=0.
Moreover,different from the terrestrial networks,the propagation delay of SCNs cannot be neglected,especially for those tasks executed in the gateways.Hence,the propagation delay of the UTkcan be represented by
3.1.2 Computation model
In this paper,one task can be executed locally or offloaded to one of the edge computing servers[39].For the task processed locally,the computing latency of the UTkcan be obtained by,
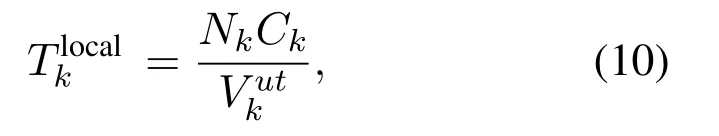
wherein CPU cycles/s is the computation resource of UTk,andCkin CPU cycles/bit defines the number of CPU cycles required to process one-bit of task data in this paper.
Similarly,the computing latency of the UTk,who offloads its task to the satellite,can be denoted as,
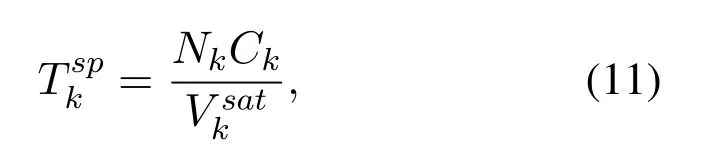
whereis t he computing resource allocated by the satellite.In the scenario of SCNs with RTO,the task generated by the UTkcan be handled by one gatewaym,so the computing latency of the UTkcan be obtained by,
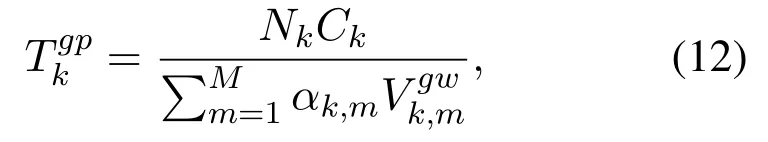
whereis the computing resource allocated by the gatewaym.
IV.PROBLEM FORMULATION AND SOLUTION FOR SCNS
In this section,we shall investigate the joint computing and communication resource allocation problem for SCNs with and without RTO,which aims to minimize the total latency.With the feasible feeder links,UTs can offload their task to the gateways with the edge server.Hence,the satellite can make two types of decisions for each UT,λk= 1 for local processing,λk= 0 for the remote processing.Furthermore,the association indicatorφk= 0 andφk= 1 respectively represents weather or not satellite processing,and the association indicatorθk= 0 andθk= 1 denotes weather or not gateway processing.If SCNs cannot keep a feasible feeder link and obtain the resource of the gateway,the UTkcan only offload the tasks to the satellite,θkandαk,malways equal to 0.
4.1 Problem Formulation
Under the scenarios of SCNs with and without RTO,the communication and computation resource of the satellite and gateways will be jointly allocated to UTs,the response latency for thekth UT can be denoted as,
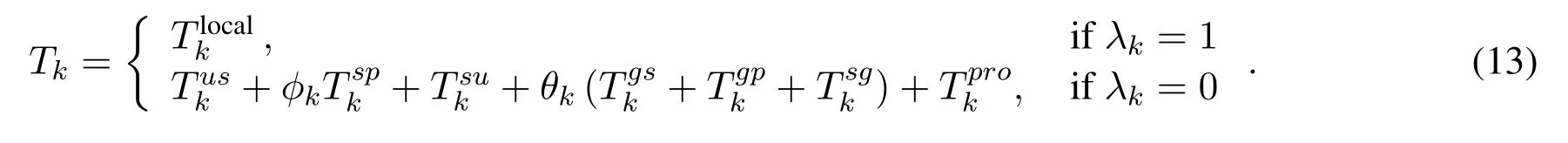
In this paper,we intend to minimize the weighted sum-latency of all the UTs.The problem can be formulated as,

In (14),γkis defined as the weighted coefficient for thekth UT,which is used to guarantee the fairness among UTs.andmeans that the offloading UTs will share the communication resource of its associated satellite.denotes that the UTs with association indicatorφk= 1 will share the computation resource of its associated satellite.Moreover,andjointly guarantee that the communication and computation resource allocated to UTs will not exceed the corresponding constraints for its associated gateway.presents that the task ofkth UT can only be executed once.Andrepresents that one UT can only offload its task to one of the gateways.It can be found that the problem formulated in(14)is a mixed-integer programming problem,and it is an NPhard problem.With many decisions and constraints,the NP-hard problem of(14)is complex to solve.
4.2 Optimal Solution
Since it is hard to find an optimal solution for the problem formulated in (14),we decompose the optimization problem of (14) into three sub-problems.The first one is to determine whether or not offloading the tasks.If the tasks are allocated to be executed in the edge servers,the corresponding problem is to choose the edge server(satellite and gateways)to offload the tasks.Once the offloading decisions and the association indicators of each UT are made,how to allocate the communication and computation resource of the associated satellite and gateways to each UT needs to be tackled.
In(14),the management of computing and communication resource will be affected by the offloading decisionλkand the association indicatorαk,m,φk,θk.To tackle this problem,λk,αk,m,θkandφkare assumed to be fixed.In this way,we can firstly obtain that how to allocate the communication and computation resource of the associated satellite and gateways.And the objective of(14)can be rewritten as,
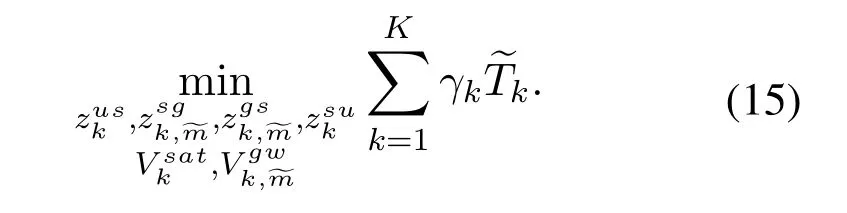
In (15),the constraints forandare the same as that in(14),andTkcan be got withλk,αk,m,θkandφkbeing assumed to be fixed.Due to the fixed offloading decision and the association indicator of each UT,the latency of local processing and propagation can be neglected.Thus,can be expressed in detail as.
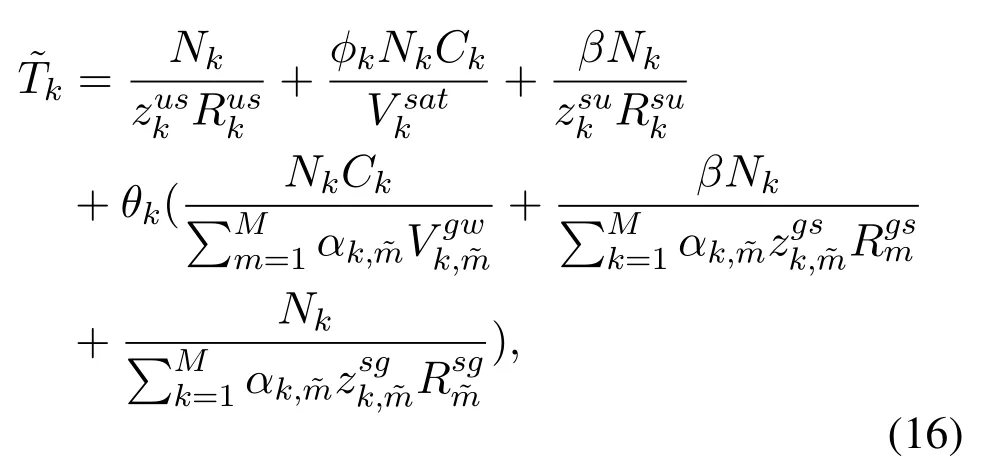
Theorem 1.With(15),the optimal solution for computing and communication resource allocation can be got by adopting KKT conditions.
Proof.The Lagrangian function of the convex optimization problem defined in (15) can be expressed as,
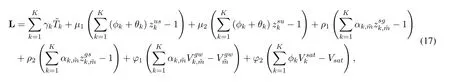
whereµ1,µ2,ρ1,ρ2,ϕ1andϕ2are Lagrangian multipliers,and they satisfyµ1≥0,µ2≥0,ρ1≥0,ρ2≥0,ϕ1≥0 andϕ2≥0.According towe can obtain the optimal value ofSimilarly,the optimal solution for joint computing and communication resource allocation can be got with the offloading decisionλkand the association indicatorαk,m,φk,θkbeing fixed.Therefore,the weighted sum-latency of all UTs with the fixed offloading decision can be expressed as,
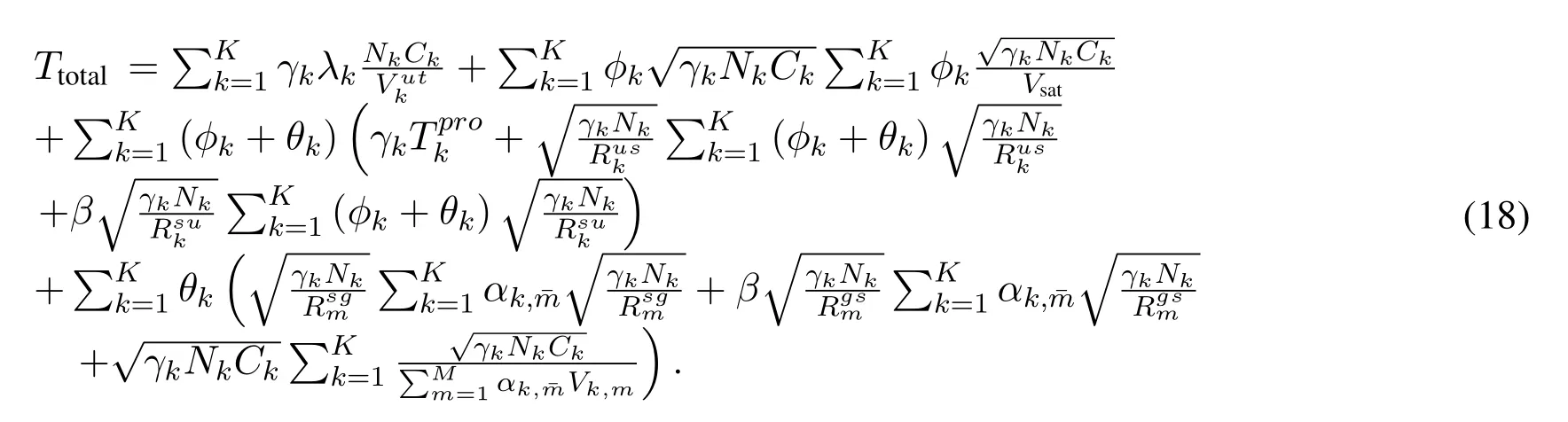
Next,the offloading decision and association indicator of each UT should be optimized.For the scenario of SCNs without RTO,once the UTkdecides to offload to the edge server,the satellite is the only choice,θkandαk,malways equal to 0.Hence,when we optimize the offloading decision and association indicator of each UT,the scenario of SCNs without RTO can be regarded as a special case for SCNs with RTO,whose association indicatorθkandαk,mis 0.It is obvious that the enumeration method can be used to obtain the best combination of the offloading decision and association indicator of each UT.
1)A Brute-force solution:As a benchmark in this paper,we firstly adopt a Brute-force solution to find the optimal offloading decisionλkand association indicatorφk,θk,αk,mof each UTk,which will enumerate all the possible decisions and then choose the optimal decision with the minimum weighted sum-latency of all UTs under the constraints of the resource.Algorithm 1 shows the detail of the Brute-force solution.

Algorithm 1.JCCRA based on Brute-force solution.Input: K,M,V utk of each UT k,V gwm of each gateway m,Vsat.Output: the optimal offloading decision λk and association indicator φk,θk,αk,m of each UT k.1: enumerate all the combinations of the optional offloading decision and association indicator of each UT k.2: via (18),obtain the weighted sum-latency of all the feasible combinations and then find the combination of the offloading decision with the minimum weighted sum-latency of all UTs.3: return the optimal offloading decision and association indicator of each UT k.
Although the optimal offloading decision and association indicator can be found with a Brute-force solution,the computational complexity of the Brute-force solution will grow exponentially along with the increase of the tasks.Therefore,JCCRA-GM based on a game-theoretic approach and matching theory with low complexity will be introduced.
2) JCCRA-GM:As mentioned above,the joint computing and communication resource allocation problem can be decomposed into three sub-problems,the optimal resource allocation can be obtained via(18).Then,in the process of optimizing the offloading decision and association indicator of the scenario with multiple gateway stations,where to offloading the task can be addressed first.Therefore,a matching theory is adopted in this paper to optimize the association indicatorαk,m,φkandθk,while the offloading decisionλkbeing assumed to be fixed.
Definition 1.A matching game is that two sets of players(K,M ∪S)rank one another to achieve a suitable matching η:K → M ∪S,while M ∪S={0,1,...,W}denoting the union set of the edge servers (the satellite and gateways) and W=M.For each edge server w,a pair of UT-satellite or UTgateway under η can be expressed as(k,w)∈η.
In the matching,if UTk ∈Kis associated with the edge serverw(w >= 1),thenm=w,αk,m=1,φk= 0 andθk= 1,which means that the UTkoffloads its task to he gatewaym.Meanwhile,if UTk ∈Koffloads its task to the satellite,thenw= 0,αk,m= 0,φk= 1 andθk= 0.Thus,the optimization ofαk,m,φkandθkcan be reformulated as a matching game.Lwis a collection of UTs connected to thewth edge server.
Moreover,each player’s decision on UT-satellite or UT-gateway association is influenced by other players in the system,therefore this is a many-to-one matching with externality problem.To tackle the matching game,a utility function that represents the weight-sum latency based on the current matching resultηof the system can be expressed as,
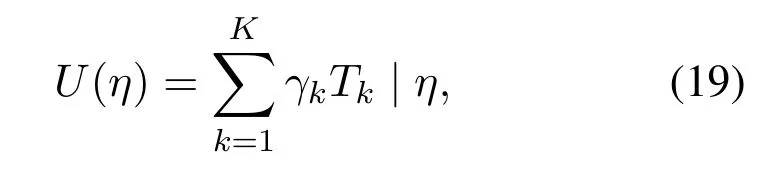
whereTk | ηdenotes the experienced latency ofkth UT with the matchingη,and the minimization ofU(η),denoted asUmin(η),can be achieved by solving the problem defined in(15).
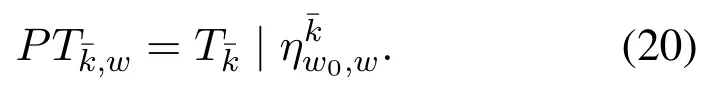
Thus,the preference list of each UTcan be calculated with(20),and the most preferred gatewayw∗is the one that minimizes its experienced latency.Ifw∗≠w0,the UT sends an association proposal tow∗.Since there may be multiple UTs that send association proposals to the same edge server,the edge server needs to select its most preferred UT to minimize the edge server preference expressed in(21).
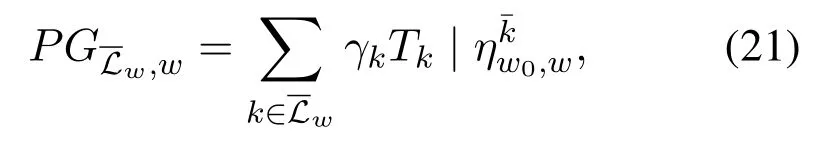

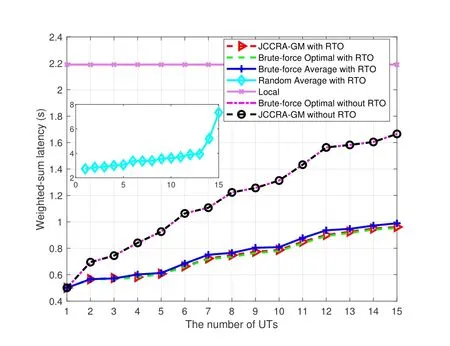
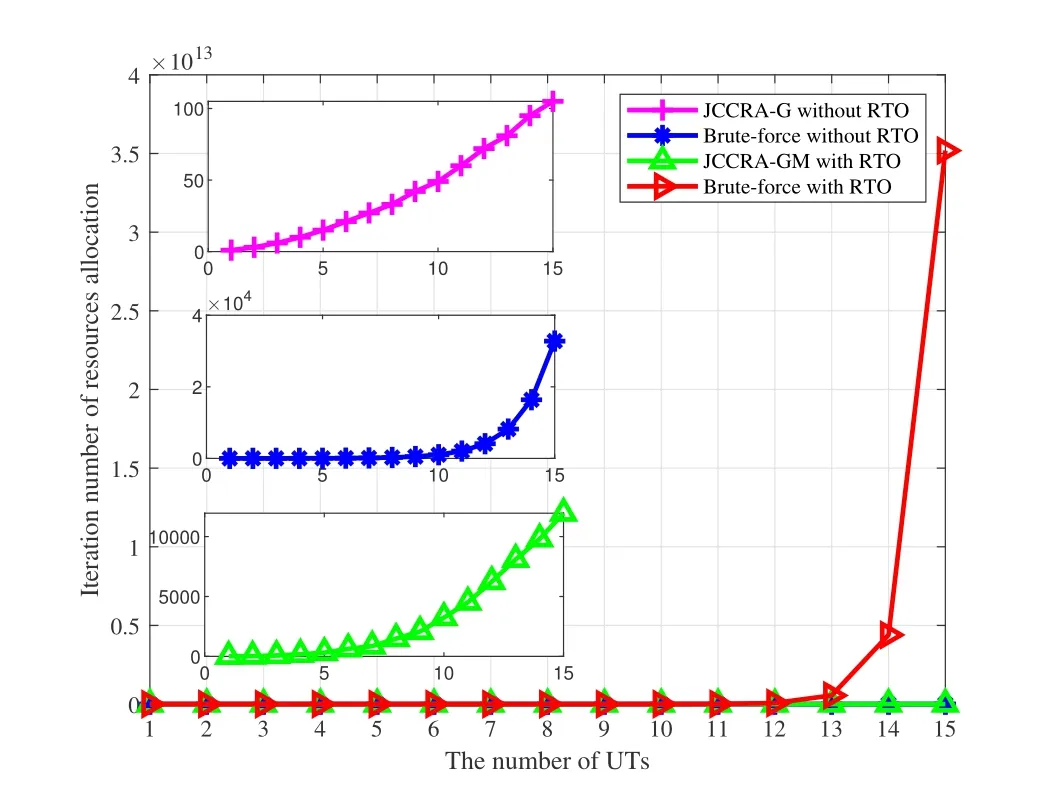
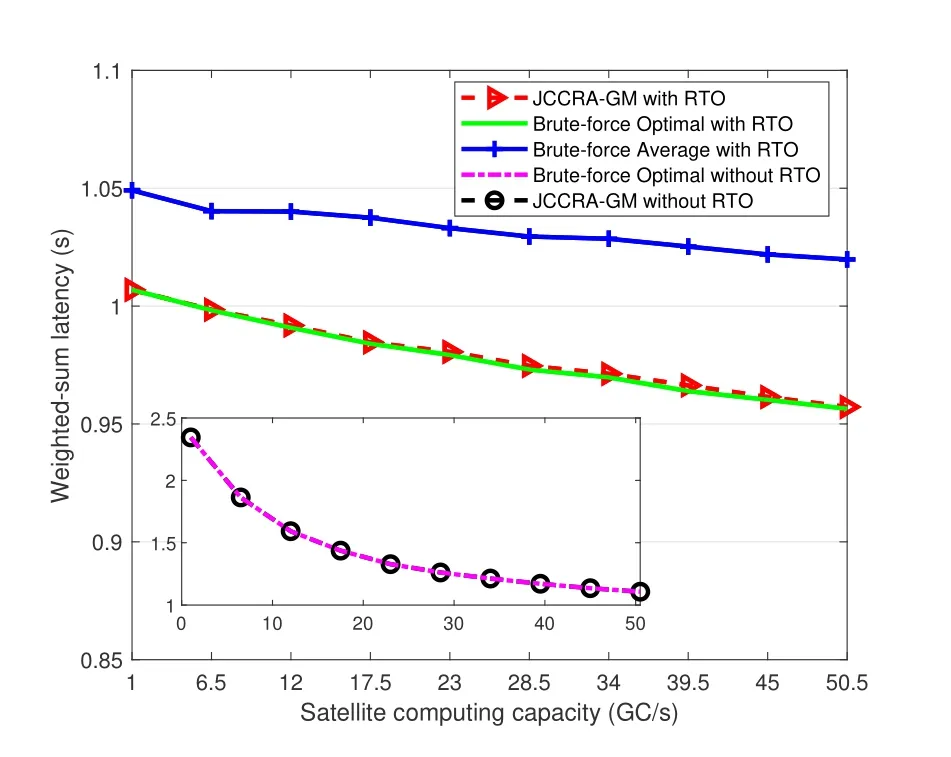
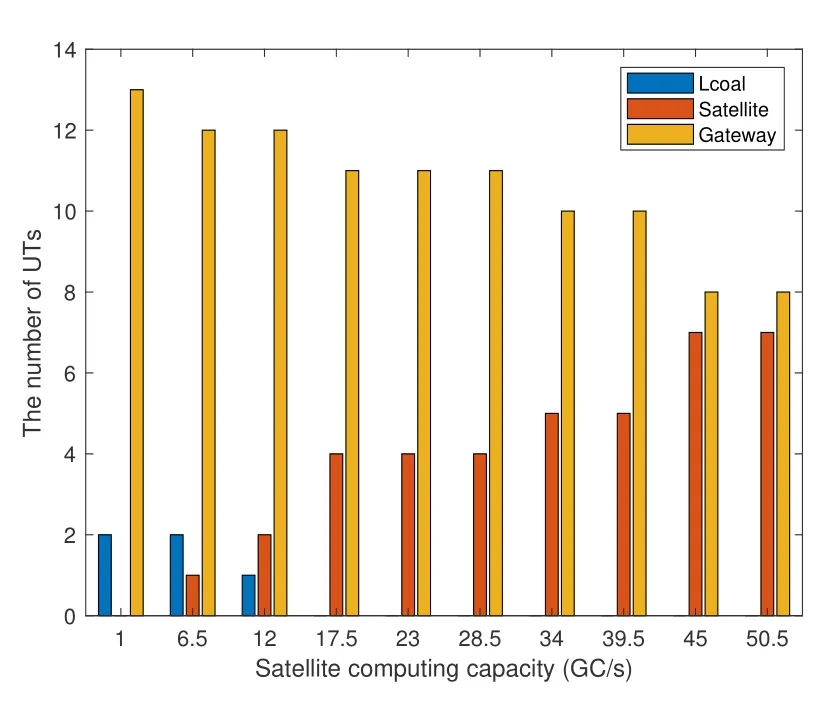
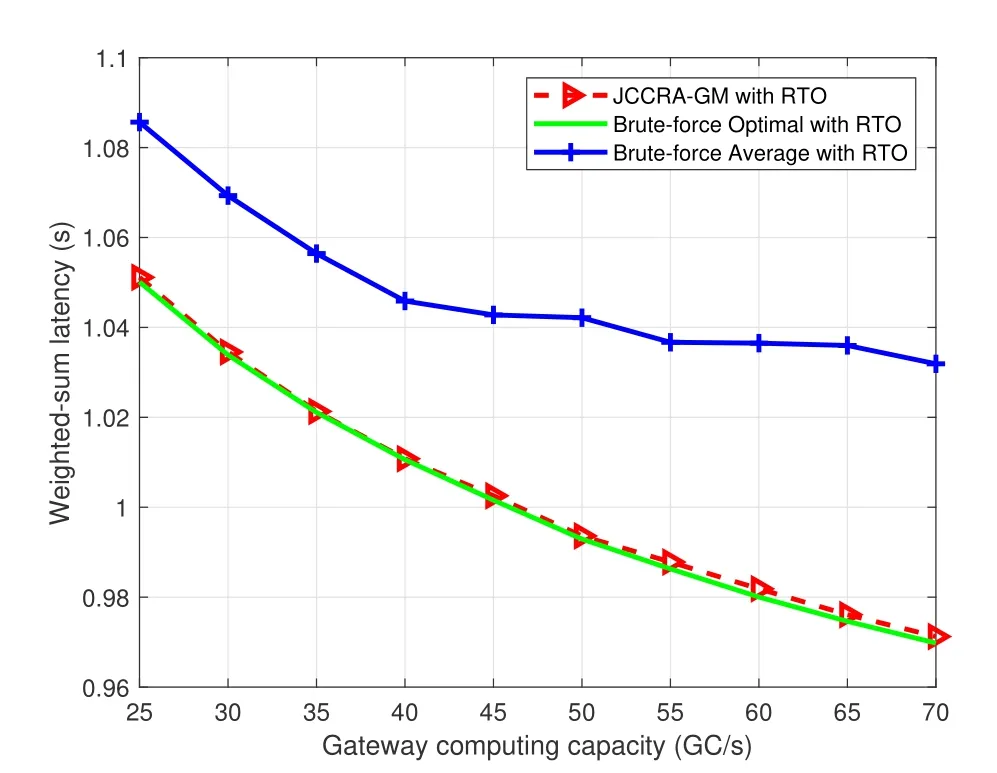
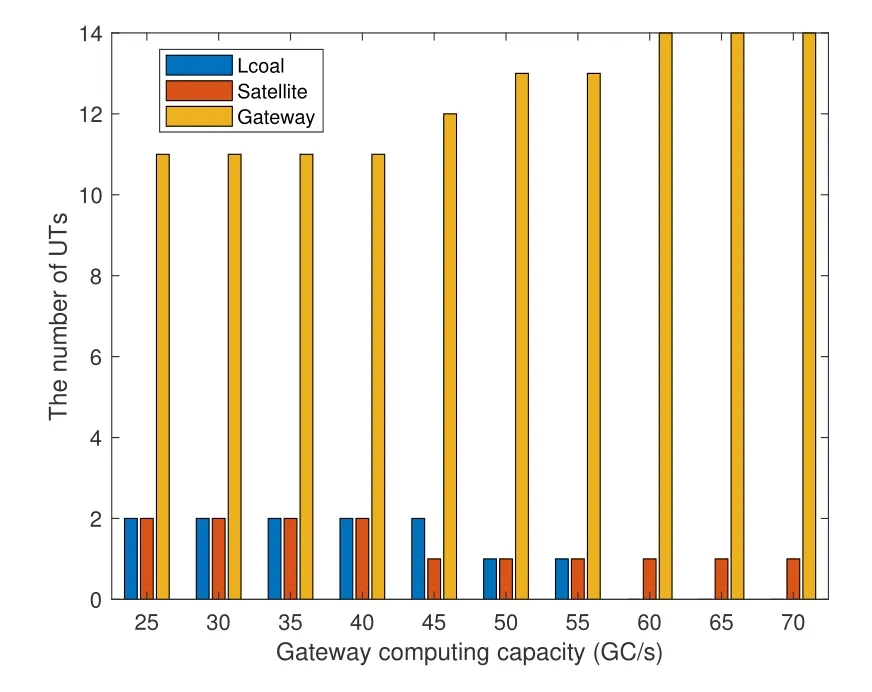
Algorithm 2.JCCRA-GM for searching the association indicator.Input: K, M, S, V gwm of each gateway m,V ut k of each UT k,λk.Output: a pairwise stable matching η∗.1: Initialize: each UTs whose offloading decision λk = 1 is associated to a randomly selected edge server(gateway or satellite),the matching is η.2: phase I-Heuristic Search 3: while 1 4: each UTs whose offloading decision λk = 1 calculates its preference list and find the most preferred edge server w∗.5: if m∗≠m0 6: each terminal sends association proposal to the preferred edge server w∗.7: each edge server calculates its most preferred UT k∗.8: if Umin(ηk∗w0,w∗) Please note that the preference ofkth UT ormth edge server is affected by the matching relationships of other UTs or edge servers.Due to the externality,we adopt the notion of swap-matching and a stability concept of pairwise-stable to keep the convergence of the matching game,and its feasibility has been proved in[40]. Definition 2.A UT-satellite or UT-gateway association(k,w)∈η is influenced by the other UT-satellite or UT-gateway association(l,n)∈η,(l,n)≠(k,w).A swap-matching in this paper can be represented by={η(k,w)(l,n)}∪(k,n)∪(l,w). Definition 3.A matching in this paper is pairwise-stable if there does not exist swap-matchings suchthat:which means that ex-changing any two pairs of UT-satellite or UT-gateway cannot make the latency utility function Umin(η)lower. With these definitions,the proposed joint computing and communication resource allocation based on matching theory is shown in algorithm 2. According to algorithm 2,the association indicator of each UT and the weighted sum of latency can be obtained when the offloading decision is assumed to be fixed.With the two schemes mentioned above,a game-theoretical based solution with low complexity will be adopted to make an offloading decision for each UT. As a powerful tool to study the competition among the rational players,game theory has been widely used in SCNs to obtain the feasible resource allocation scheme and satisfy the different service requirements for those players[41].Therefore,we will adopt game theory and propose a game-theoretic approach for the offloading decision in this section. In this offloading decision game,the rational players are all of the UTs,and the strategy of players is the offloading decision of task execution(execute the task locally or offloading to the edge servers).As for the problem that where to offload the tasks,it can be obtained based on algorithm 2.Letλkandλ−k= (λ1,..,λk−1,λk+1,...,λK) respectively denotes the offloading strategies of the playerskand the offloading strategies of all the players except of the playerk.According to [9],the performance metrics in this offloading decision game can be defined as the weighted sum-latency of all the players,which can be obtained via the offloading decisions of all the UTs,algorithm 2 and(18).Hence,the cost function of playerkcan be represented as, whereTk | λkrepresents the response latency for thekth players with the offloading decisionλk. Algorithm 3.JCCRA-GM.Input: K,V ut k of each UT k,Vsat.Output: the optimal offloading decision λk of each UT k 1: Initialize: For the set of the offloading decision is λ,all the UTs choose to execute the task locally(λk = 0,∀k ∈K),whose weighted sum-latency of all the UTs is T∗total.2: while 1 3: for k =1 to K do 4: update λ∗←λ.5: if λ∗k =0 6: λ∗k =1 and λ∗−k remains unchanged.7: via (18),algorithm 2 and the set of the updated offloading decision λ∗,calculate the weighted sum-latency Fk(λ∗k,λ∗−k) of all the UTs.8: end if 9: end for 10: find the updated offloading decision λ∗k of the kth UT that minimize the cost function Fk(λ∗k,λ∗−k).11: if Fk(λ∗k,λ∗−k) With the cost function(15)and other players’decisionsλ−k,each playerkwill choose the best offloading decisionλ′kso as to minimize the cost function. Therefore,the offloading decision-making problem can be formulated as a strategic game,whose Nash equilibrium for the offloading decision game is presented below. Definition 4.A strategic game with K UTs can be defined by G={K;λ1,λ2,...,λk;F1,F2,...,Fk}.Given the offloading decision λ−k of other players,each player k aims to find the best offloading decision λk to minimize the cost function Fk.And the objective of the strategic game is to search the offloading decision set {λ1,λ2,...,λk} to minimize the weighted sum-latency of all the UTs. Definition 5.A Nash equilibrium of this offloading decision game is that no player further obtains the additional gain of the cost function by changing only its own strategy λ′k,which means Fi(λ′k,λ−k)>Fi(λk,λ−k),∀k ∈K. For the above offloading decision game,both the numbers of the players and their strategies are finite.Hence,the offloading decision game in this paper can reach Nash equilibrium after several rounds of the game according to the NE existence theorem.Algorithm 3 shows the detail of the game-theoretical solution. As shown in algorithm 3,the offloading decisions of all the UTs are set to 0 at the beginning of the algorithm.Then,given the offloading decisionsλ−kof other UTs,each UTkwill change its strategy to minimize the cost functionOnly one UT can obtain the offloading decision update opportunity for each round of the game.In this way,after several rounds of the game,no player can further reduce the weighted sum-latency of all the UTs if all other UTs keep their strategies,which means that the offloading decision game reaches to a Nash equilibrium. Finally,with the set of the offloading decisionλ−k,algorithm 2 and (18),the sub-optimal solution of the joint computing and communication resource allocation problem in the scenarios of SCNs with RTO can be obtained. Problem (14) with discrete variables and continuous variables in this paper is a mixed-integer programming problem,which is an NP-hard problem and complex to solve directly.This mixed-integer programming problem can be decomposed into several sub-problems to decrease the computational complexity,and an approximate optimal solution can be obtained through successively and literately solving the sub-problems[42],while the equivalence is guaranteed. The complexity of the proposed algorithm mainly consists of three parts,which are corresponding to three sub-problems and its solution.For the problem that how to allocate the constrained communication and computing resource under the given offloading strategy,formulation (18) in this paper gives the analytic solution,and its complexity is linear with the number of UTs and gateway stations,which can be represented as O(K + M).For the sub-problem that whether to offload the tasks,a game-theoretic approach is proposed.For the worst case that all the UT choose to offload its task,the number of resource allocation is O(K(K+1)/2).For the first sub-problem that where to offload the tasks,a many-to-one matching game model with externality is adopted,and it consists of two phases,for the phase of heuristic search with the worst case that all the UTs prefer one gateway station or satellite,the number of resource allocation is O(N(N + 1)(K + 2)/2).At the phase of swap-matching evaluation,the worst case is to swap all the UTs,the number of resource allocation is O(N(N−1)/2).Therefore,the total complexity of the many-to-one matching game model with externality is O(N(N−1)/2+N(N+1)(K+2)/2).The total complexity of the proposed algorithms is the product of the three sub-algorithms.Figure 4 in this paper shows the simulation results of the complexity of our scheme and the Brute-force method(O(2K ×(M+1)K)).As shown in figure 4,the proposed JCCRA-GM scheme has much lower computation complexity. For a given vector of offloading decisions and association indicators,the problem for resource allocation is convex,and the Karush-Kuhn-Tucker (KKT) conditions can be adopted,which is convergent; Second,the association indicators in this paper are abstained by a many-to-one game,and it consists of two phases,each phase set the condition of termination(Step 5 and 15 of Algorithm 2),and the convergence of many-toone game with externality has been proved in[40].Finally,for the game-theoretic scheme,the termination condition state in step 10 of algorithm 3 in this paper,and the proposed scheme will get convergent when no user can further reduce the weighted sum-latency of all the UTs by changing their offloading decision.For K users,the scheme will get convergent after at most K rounds.Since all of the three sub-schemes of this paper are convergent,the convergence of the proposed scheme is guaranteed.Besides,simulation results of the proposed scheme’s iteration number can demonstrate the convergence of the proposed scheme. In this section,the proposed JCCRA-GM for SCNs with and without RTO is evaluated with two referred schemes in the performance metric of the weighted sum of latency.To solve the sub-problem that whether and where to offload the tasks,the Brute-force method can be adopted,which will enumerate all the optional offloading decisions and associated indicators to find the optimal solution with high computational complexity.While for ’Random’ method,each UT randomly decides whether to offload its task and selects an edge server to associate regardless of the decisions of other users.In terms of resource allocation,optimal and average resource allocation are both considered.Here,optimal resource allocation refers to the method that utilizes the KKT conditions with the offloading decisions and associated indicators being fixed. In this simulation,the Ka-band SCNs with and without RTO are considered.The antenna gain of GEO satellite is 45dBi,and its transmission power is 20dBW[43].The EIRP(Equivalent isotropic radiated power)of gateway stations is 75dBW.And the mean of the rainfall intensity is 5 mm/h [38]Both of the two scenarios consist of one satellite and five kinds of UTs.The corresponding data size for each UT follows the uniform distribution withMbps,and the EIRP for five kinds of UTs is from 9dBW to 17dBW.For the SCNs with RTO,there are two gateways with edge servers,whose computation capacities vary from 5×1010to 7×1010cycles/s [44].The f computation capacities of the satellite are set to 1010cycles/s.The computation capacities of UTs vary from 5×108to 109cycles/s,and the number of CPU cycles required to process one-bit of task data is 1000 cycles/bit.The weights for all UTs are the same,which equals to 1/Kand represents the average response latency of all UTs.The compression ratio is set to 0.7[45]. Figure 3 depicts the weight-sum latency versus the number of UTs.It can be seen that the weight-sum latency becomes larger when more and more UTs access the network.This is because that UTs need to compete for the limited resource,such as communication resource and computing resource.It also can be observed that the proposed JCCRA-GM scheme can achieve a performance which approximately equals to the Brute-force solution with the optimal resource allocation.To validate the effectiveness of the optimal resource allocation scheme based on the KKT conditions in this paper,figure 3 plots the results of the Brute-force method with average resource allocation,which shows that it performs worse than the scheme with the optimal resource allocation.This is caused by the diversity of the tasks.Since SCNs have large coverage and serve for a variety of UTs,different UTs will have varied data size and transmission rate,this paper takes the diversity into account.Besides of the diversity of data size and transmission rate,the local processing capacities are considered as well.As shown in figure 3,the weight-sum latency of the method of‘Local’,which means that all of the UTs execute the task locally,keep a constant value along with the growth of the number of UTs,and it has the worst performance compared with the proposed schemes.Moreover,the proposed JCCRA-GM scheme with RTO outperforms the proposed JCCRA-GM scheme without RTO,especially for the large number of UTs.This trend is expected,because SCNs with RTO have more computing resource. Figure 3.Latency v.s.the number of UTs. Figure 4 presents the iteration times needed to find an optimal solution for resource allocation,which can be selected as the metric to evaluate the complexity of the proposed scheme and the baseline schemes.When the scheme obtains the optimal solution,it also gets convergent.As is shown,the iteration times of the Brute-force method that traverses all possible matches increases exponentially with the growth of UTs’number.For Brute-force method without RTO,the iteration times of resource allocation is 2K,because each UT has two optional offloading choices.As for Bruteforce method with RTO,beside of two optional offloading choices,each offloading task haveM+ 1 optional associated indicators,and the iteration times of resource allocation is 2K ×(M+1)K.However,the iteration times of the JCCRA-GM method increase slowly.When the number of UTs reaches up to 15,the iteration times for searching an optimal solution are about 1.5×104and 100 for JCCRA-GM with and without RTO,respectively.Once the optimal solution is obtained,the proposed scheme JCCRA-GM will stop and get convergent.The zoomed-in figure clearly shows that JCCRA-GM has much lower computation complexity.Therefore,compared to the Brute-force method,the proposed JCCRA-GM scheme has similar performance and lower computational complexity. Figure 4.Iteration number of resource allocation v.s.the number of UTs. Figure 5 shows the relationship between the satellite computing capacity and the weight-sum latency.With the enhancing of the satellite computing capacity,the weight-sum latency of the proposed JCCRA-GM scheme with and without RTO decreases,and always has almost the same performance as the Brute-force method with optimal resource allocation.For UTs of SCNs without RTO,it can only offload its task to the satellite,therefore,whose performance is more dependent on the computing capacity of the satellite,so its rate of descent for the weight-sum latency is larger than SCNs with RTO.Due to the deployment of the edge computing servers with sufficient computing resource in gateways,the performance of the JCCRAGM scheme only obtains a small gain.Figure 6 shows the details of the offloading decisions and associated indicators of all the UTs.Almost all of the UTs choose to offload their task.Following the increasingly sufficient computing resource of the satellite,more and more UTs associate with the satellite. Figure 5.Latency v.s.satellite computing capacity. Figure 6.The offloading decisions and associated indicators with satellite computing capacity. Similar to figure 5,figure 7 demonstrates that the weight-sum latency of the proposed JCCRA-GM scheme and the Brute-force method with optimal resource allocation is approximately the same and both decrease with the increase of the gateway computing capacity.The proposed JCCRA-GM scheme outperforms the Brute-force method with average resource allocation.When the computing capacity of the gateway grows large enough,gateways almost take on all the tasks,and the performance of the proposed scheme only depends on the resource allocation scheme.This is because that no UT can further improve its performance by adjusting its offloading decision and associated indicator when the computation capacity of gateways becomes abundant enough,which can also be observed from figure 8. Figure 7.Latency v.s.gateway computing capacity. Figure 8.The offloading decisions and associated indicators with gateway computing capacity. In this paper,the joint computing and communication resource allocation is investigated for latency optimization in SCNs with edge computing technique.Due to the intermittent feeder link,SCNs with RTO and without RTO are considered.And the joint computing and communication resource allocation problem is formulated as a mixed-integer programming problem.In order to solve this NP-hard problem,we decompose the problem into three sub-problems: a)Whether to offload the tasks? b) Where to offload the tasks? c) How to allocate the constrained communication and computing resource of the satellites and gateways for multiple UTs? Then,these three sub-problems are solved in proper order.The JCCRAGM scheme,based on a game-theoretic approach and many-to-one matching game with externality,is proposed to minimize the weight-sum latency.Simulation results demonstrate that the proposed JCCRAGM scheme can achieve near-optimal performance with very low computational complexity. In this paper,the main objective is to obtain the optimal offloading strategy and minimize the latency of data processing and transmitting,one satellite and multiple gateway stations are considered,where the satellite can collaborate with gateway stations to process the offloading tasks and the power of satellite for task processing is assumed to be enough.In the future,LEO satellite constellation,massive users’access,collaboration computing among satellites,user handover federated learning model and energy-efficient offloading strategy should be investigated. ACKNOWLEDGEMENT This work was supported by the National Natural Science Foundation of China (Grants 61971054 and 61601045) and Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory Foundation(HHX21641X002 and HHX20641X003).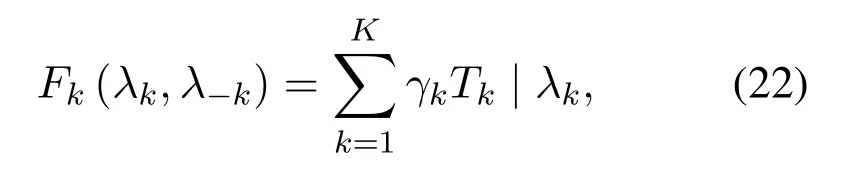

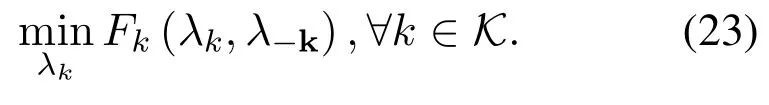
V.ANALYSIS OF THE PROPOSED SCHEME
VI.NUMERICAL RESULTS
VII.CONCLUSION
VIII.FUTURE RESEARCH

