Information-Defined Networks: A Communication Network Approach for Network Studies
Wenjie Jia,Tao Jiang,*
1 School of Electronic Information and Communications,Huazhong University of Science and Technology,Wuhan 430074,China
2 Wuhan National Laboratory for Optoelectronics,Huazhong University of Science and Technology,Wuhan 430074,China
Abstract: The research of complex networks facilitates the progress of various disciplines,including biology,chemistry,social science,computer,and communication engineering.Recently,it is popular to utilize complex networks to study the communication networks,such as designing efficient routing strategies and robust communication networks.However,exploiting the advantages of communication networks to investigate networks in various disciplines beyond telecommunications is still in infancy.Because of this situation,this paper proposes an information-defined network (IDN) framework by which a complex network can be abstracted as a communication network associated with multiple intelligent agents.Specifically,each component and dynamic process in this framework can be defined by information.We show that the IDN framework promotes the research of unsolved problems in the current complex network field,especially for detecting new interaction types in realworld networks.
Keywords: network data analysis; label detection;complex network; communication network; network evolution
I.INTRODUCTION
A complex network is a network with non-trivial topological features,such as self-organizing,selfsimilarity,small-world,and scale-free [1].Generally speaking,many complex systems can be modeled as complex networks for analyzing their properties in practice [1,2].As a special case,the associated researches on communication networks,such as ad-hoc networks[3],wireless sensor networks[4]and internet of everything[5,6],can be facilitated by the theories and techniques from complex networks.Specifically,it is found that the peculiar structural characteristics of many complex networks support efficient communication without global knowledge[7].This finding inspired a series of routing strategies that do not rely on the global connectivity information of the communication network[7–12].Furthermore,it is shown in[13]that the interdependent feature of complex networks would lead to cascading failures,which significantly undermined the robustness of the network.This discovery opened an avenue for investigating the robustness and fragility of communication networks from a complex network perspective [14–18].Additionally,complex networks also play an essential role in studying power networks,biological networks,computer networks,transportation networks as well as social networks.
However,in addition to the non-trivial topological features,such as small-world and scale-free,resource exchanging through networks is a universal phenomenon in both natural and man-made complex systems.For example,in a brain network,various neurons communicate with each other through some biological signals.An online social network,as another example,is an information exchange platform that relies on the Internet.Regarding the resources transmitted in real-world networks as information,we can view these networks as communication networks.This observation motivates us to ask a question: can some unsolved problems in current complex networks be solved from a communication network perspective?
To answer this question,we introduce as follows an unsolved knowledge discovery problem in complex networks,which has attracted lots of attention from network scientists and engineers specialized in the information and communications technology(ICT).
Big data networks original from the Internet,such as online social network,citation networks,webpage networks,and peer-to-peer networks,emerge as the transition from an industrial society to an information society driven by the continuous developments in ICT.These years,it is very popular to design communication networks by fully taking into account the users’experience.This trend motivates researchers in ICT to study the users’ features and interactions between users from these big data networks.As a consequence,it has attracted a lot of attention from the ICT to data mining and data discovery in these big data networks.Commonly,these networks involve multiple interaction types[2].In practice,these types suggest essential information on the interactions between components,but not all of them have been discovered yet.Thus,detecting the previously-undiscovered interaction-types (PUITs) is essential for deepening our understanding of the data.Additionally,its solutions would benefit researchers in mining new features in a wide range of datasets,for instance,to discover new interactions between proteins in protein-protein interaction networks.Although previous studies have discussed the edge label detection problem [19,20],detecting PUITs is a new one with new challenges.The first and unique technique for solving this problem was developed based on a novel temporal network model,namely the degradation-evolution (DE)network model[21].Therefore,we arrive at a crucial but unsolved problem in network science,i.e.,detecting PUITs in networks which the DE model can not mimic.
Focusing on the above problem,we find that the DE model is a special case of the network formation model deduced by the IDN framework.Finally,we conclude that the IDN framework has the potential to tackle the crucial but unsolved problem,i.e.,detecting PUITs in networks beyond the scope of the DE model.This finding gives a“Yes”answer to the main question.
The remainder of this paper is organized as follows.Section II describes the foundation of the framework—information-defined network components.Section III introduces how information flows drive network to evolve in the IDN framework.Section IV presents the relation between IDN framework and the DE model.Section V concludes this paper.
II.INFORMATION-DEFINED NETWORK COMPONENTS
Our modeling approach builds on the intuition that in complex systems,interactions (described by directed edges in network science) can often be interpreted as suitable supply-demand relations.For example,in online social networks like Twitter.com,a directed edge where uservifollows uservjindicates thatvidemands “information” (e.g.,in the form of texts,photos,and videos) fromvj.We take citation networks as another example.Papervihaving an out-edge connected to papervjimplies thatvirequires some information provided invjto support some of its claims.Inspired by these observations,we assume an interaction represents the supply-demand exchange of some“resource”.Motivated by the basic idea of recommender systems [22]and natural language processing[23]that vectors can represent products or words,we assume that resources exchanged by the agents can be also represented by vectors consisting of nonnegative real numbers.We refer to this representing vector as a piece of information or a (digital) signal.Specifically,we define a signalSas a finite sequence ofMnon-negative real numbers,(S[1],...,S[M]),where(without loss of generality)Mis a large enough positive integer andS[h]represents theh-th entry ofSforh=1,2,···,M.Hence,all possible signals span a spaceS=[0,∞)M.
For a real numbers ≥0,define
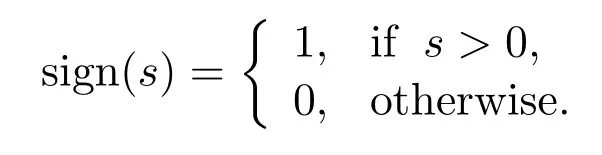
For signalS= (S[1],S[2],···,S[M]),define sign(S)=(sign(S[1]),sign(S[2]),···,sign(S[M])).Two signalsS1andS2belong to the same signal category if and only if sign(S1)=sign(S2).S1is weaker thanS2,denoted byS1≤S2,ifS1[h]≤S2[h]for anyh=1,2,···,M.
A signal can be interpreted as a piece of information(message)that may involve several topics.We employ nonzero vectors inC={0,1}Mto represent such topics.Forh= 1,2,···,M,we define theh-th primitive topic as the topic corresponding to the unit vectorIh,whoseh-th entry is one,whereas all the other entries are zeros.For example,suppose that two pieces of news about football are denoted by (0,2,0) and(0,3,0),whereas a piece of news about COVID-19 is written as (4,0,0).Hence,we can useI2= (0,1,0)andI1= (1,0,0) to denote football and COVID-19,which are primitive topics in this scenario.Naturally,signalScontainsI1-type(I2-type)information if and only ifS[1]>0 (S[2]>0).More generally,for a given topicC,we say that signalScarriesC-type information,ifS[h]>0 for allh ∈{h|C[h]= 1}.TheC-type information carried byScan be written asC ◦S= (C[1]S[1],C[2]S[2],···,C[M]S[M]),where “◦” refers to the Hadamard product.It follows that if signalScarriesC-type information,thenC ≤sign(S).Especially,the total information carried byScan be represented byS ◦I,where
In IDNs,nodes are viewed as intelligent agents(Figure 1),who are the sources(or suppliers)of information flows.We assume that agents generate signals at random via a signal generator they are endowed with.Specifically,agentvi’s signal generator,denoted byqi,can be represented by anM-length sequence of probability distributions (Oi1,Oi2,...,OiM),where eachOijis with support in [0,∞) and bounded expectation,for 1≤j ≤N.Therefore,signals created byviare sampled fromqi.For a topicC,vi’sC-type information sub-generator can be expressed asqi|C(qirestricted toC).
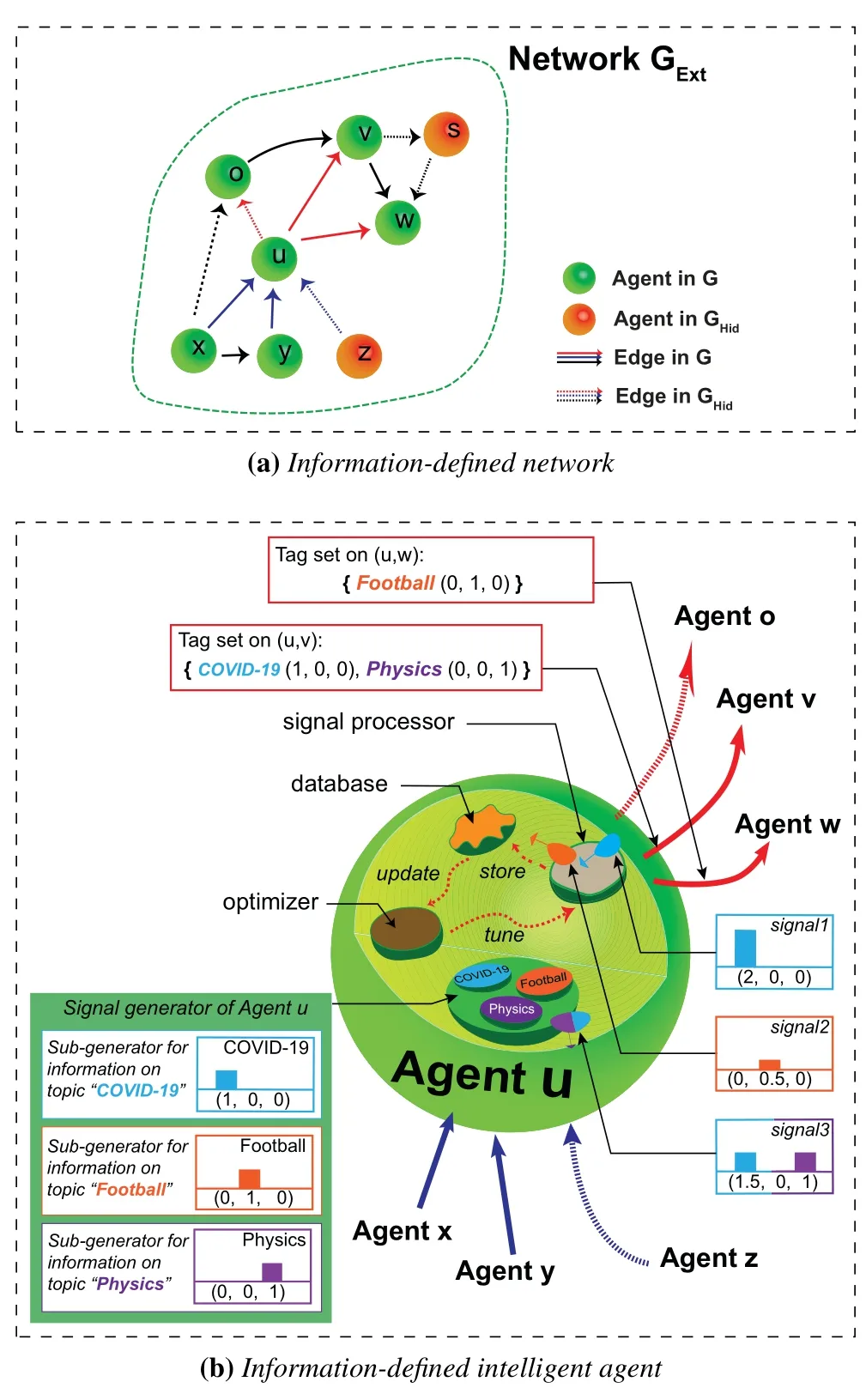
Figure 1.Information-defined network framework.(a)Information-defined network consists of the observed network G and its hidden propagation network GHid.(b)The intelligent agent in the IDN framework consists of six components: the signal generator,signal processor,database,optimizer,signal input channel(outgoing links represented by thick red arrows) and signal output channel (incoming links represented by thick blue arrows).
Both the signal generator and the sub-generators of a given agentvjare unknown to other agents.Agentviseeks to learn which topics another agentvjcan produce based on all the signals generated byvjthat she previously received.Specifically,at timet,agentvideems thatvjcan produceC-type information,ifvihas receivedC-type information carried by signals generated byvj(i.e.,there existsS ∈Si,j(t),such thatC ≤sign(S),whereSi,j(t)denotes the collection(see the definition of collections in Appendix A)of all the|Si,j(t)|signals generated byvjand received byviup to timet).See a more general case in Appendix B.
As intelligent agents,nodes have signal processors,and react appropriately to the received signals according to the processed results (Figure 1).For example,in online social networks,incoming signals drive nodes toward various reactions,e.g.,replying,forwarding or reporting.For signalS ∈Sand topicC ∈C,we denotevi’s response to theC-type information carried bySasBi(S|C),whereBi(S|C)is a non-negative real number that quantifies how useful the information is perceived byvi.For brevity,we defineBi(S) =Bi(S|I).For a label setC′={C1,C2,···,Cs},we further defineBi(S|C′) to be agentvi’s composite response to multiple pieces of informationS ◦C1,S ◦C2,···,S ◦Cs.
We require the response model to obey three principles: (1) zero signal,denoted by 0,has zero response to agents; (2) the composite response to multiple pieces of information in a signal respects the superposition principle as many response models studied in signal processing [24]do — for example,Bi(S|{C1,C2}) =Bi(S|C1) +Bi(S|C2)−Bi(S|C1◦C2) (see more details in Appendix C);and (3) a message should provide higher response than messages weaker than it (i.e.,ifS1≤S2,thenBi(S1|C)≤Bi(S2|C)for anyC ∈C).Many models in signal processing respect these properties [24],such as a linear response model defined by the equationBi(S|C) =Fi ·(S ◦C),whereFiis anMdimensional non-negative real vector associated with agentvi.See another example of response models in Appendix G.
Information also defines edge-level properties.At timet,each edgevi →vjis associated with a set of tags,denoted byXi,j(t).Intuitively,Xi,j(t)represents the set of topics about whichvidemands information fromvjat timet.For example,agentvi,a Twitter user,begins to seek information about COVID-19 (represented by tagI1)from the World Health Organization(represented by agentvj) at timet.Thenviforms a linkvi →vjwith a tag set composed of a single elementXi,j(t) ={I1}.Naturally,Xi,j(t) =∅if a link fromvitovjdoes not exist at timet.In our framework,self-edges are forbidden (i.e.,Xi,i(t) =∅for anyiandt).
Each intelligent agent is in full charge of her/his outedges.Specifically,for two different intelligent agentsviandvj,the tunable tag setXi,j(t)is merely managed by agentviand calledvi’s linking strategy tovjat timet.On the one hand,agentvi’s different linking strategies tovjpresentvi’s different information demands on suppliervj.On the other hand,agentvj’s information supply is independent withvi’s linking strategies to her/him and meetsvi’s different information demands on her/him in varying satisfaction degrees.For a givenXi,j(t),its satisfaction degree for agentviis quantified by a utility functionD(Xi,j(t)).Here,D(Xi,j(t))isvi’s average response to the specified information in the received signals generated byvjup to timet.Specifically,
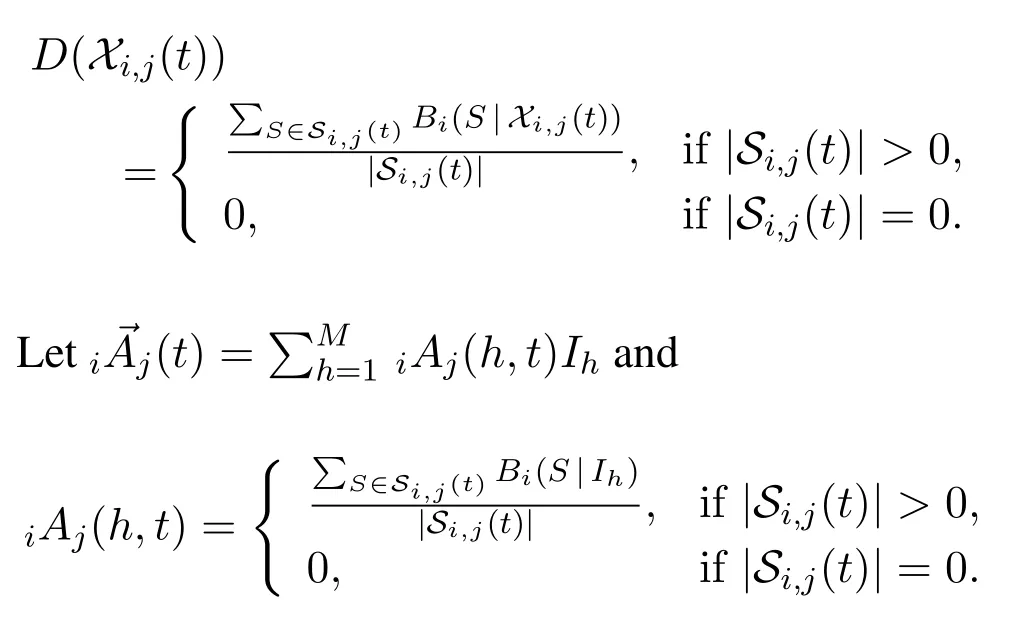
Note thatiAj(h,t)isvi’s average response toIh-type information generated byvjand received byviup to timet.Thus,iAj(h,t)is a score ofvj’sIh-type information supply ability scored byviat timet.
Let“∨”refer to the element-wise OR operator.For instance,(1,1,0)∨(1,0,0)=(1∨1,1∨0,0∨0)=(1,1,0).SupposingXi,j(t) ={C1,C2,···,Cs},where tagChis a nonzero vector inCforh=1,2,···,s,we define∨Xi,j(t)=C1∨C2∨···∨Cs.In addition,we define∨Xi,j(t) = 0 forXi,j(t) =∅.Denoting∨Xi,j(t)asXi,j(t),we can write
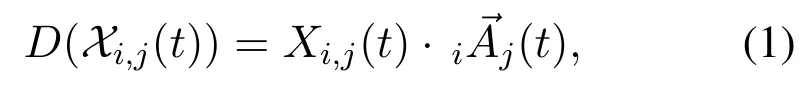
(see Appendix C).Eq.(1) shows thatXi,j(t) determines the utility ofXi,j(t).We callXi,j(t)vi’s vectorvalued linking strategy tovjat timet.Further,agentvi’s linking strategy at timetis defined to be a matrix,
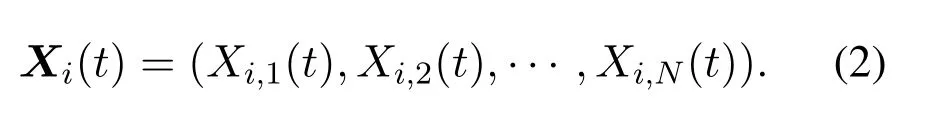
According to the IDN framework,networks emerge out of multilayer interactions among intelligent agents,and they are endowed with hidden “multilayer” structures.For a tag (nonzero vector)C ∈C,we define theC-type layer of G(t) to be the subnetwork consisting of all the edges in{vi →vj ∈G(t)|C ≤Xi,j(t)}and all the agents involved in these edges.Thus,there exist at most 2M −1 nonempty layers G(t),since there are 2M −1 tags inC.This multilayer structure is a natural consequence of underlying interactions that involve multiple tags.
III.INFORMATION-DRIVEN NETWORK EVOLUTION
In our framework,the direction of information flows is opposite to the direction of the directed edges.For a network G,there always exist many hidden roads for signals,which extend the original network.Intuitively,this corresponds to our experience that every day,we are exposed to information from many different sources; however,available data might only include information on commitments to a restricted number of sources.Besides,it also naturally accommodates for the existence of relationships that are not included in the data due to missing links[25].We denote as GHidthe hidden propagation network of G.
We denote as GExtthe extended propagation network of G which comprises edges in G or in GHidand all the nodes involved in these edges.Overall,GExt= G∪GHid(see Figure 1).We assume that the hidden propagation network GHidis timeinvariant(see Appendix G for another example).The signal spreading process in G studied here is actually a spreading process over GExt.The spreading graph GSof signalSis constructed as follows: (1) we initialize GSto be an empty graph; (2)the generator ofSis the first node of GS; (3)ifvjreceivesSfromvi(implyingvj →viis an edge in the extended propagation network),we addvj →vito GS.Obviously,GSis a subnetwork of GExt.Then this propagation process,denoted by Υ,can be represented by a triple(vi,S,GS).Υ’s seed and depth are defined to byviand the length of the longest simple paths (a simple path is a path without repeated nodes)betweenviand another node in GS,respectively.
The network formation in our framework is a network evolution process driven by information flows.
At the beginning(t=0),fixing an existing strongly connected directed network GHidas the base propagation network,we construct G(0) by addingNnodes from GHid(GHidusually has more thanNnodes).No edge is added to G(0) at first.Then,re-index nodes in GHid,such thatrepresent all the nodes of G(0).
At each timet >0,a randomly chosen seed agent fromgenerates a signal which subsequently propagates over the extended propagation network of G(t)(i.e.,GExt(t)=G(t)∪GHid).We assume that the timescale of the spreading process is substantially faster than the timescale of the network formation process.That is,the propagation process,denoted by Υ(t)=(vit,St,GSt),ends before timetincreases by one.After Υ(t) ends,receivers involved in Υ(t) update their database of received signals[i.e.,Sj,it(t−1)is replaced bySj,it(t) =Sj,it(t −1)+{St}(see the definition of the operator“+”in Appendix A),for any receivervjin GSt].Then each agentvichooses the optimal linking strategy (see its definition in Eq.(2))to maximize their perceived usefulness of the information they receive.Specifically,the optimal linking strategy is a solution to a constrained optimization problem where the objective function represents the total perceived utility of the received information(see Appendix C for its derivation):

This optimization problem has two kinds of constraints: dynamic supply-demand constraints,
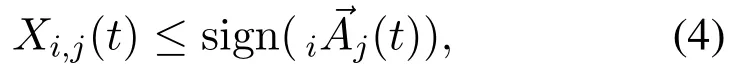
for anyi,j,t(see its derivation in Appendix D),and bounded out-degree constraints,

for anyi,t.In Eq.(5),Riis anM-dimensional nonnegative real vector associated with agentvidescribingvitotal information demand (see details in Appendix E).We callRiagentvi’s maximum demand.After each agent solves its optimization problem(see Appendix F),time increases by one.
An example of this information-driven network formation dynamics is shown in Figure 2.At timet= 0,a strongly connected network GHidis given as the propagation network for the network evolution process.The initial network,G(0),comprises three nodes,v1,v2,v3,picked from GExt.Here,we defineBi(S) =I · S=S[1]+S[2]+S[3]andRi=I= (1,1,1) fori= 1,2,3 and a signalS ∈[0,+∞)3.At timet= 1,a random node,v2,generates a random signals1= (4,2),and sends it tov1via the hidden propagation network.After receivings1,v1updates its estimation onv2’s information supply abilities from1(0)to1(1).Subsequently,her/his optimizer outputs an optimal linking strategy,X1(1) = (X1,1(1),X1,2(1),X1,3(1)) = (0,tag3,0)which is a solution to the following optimization problem:
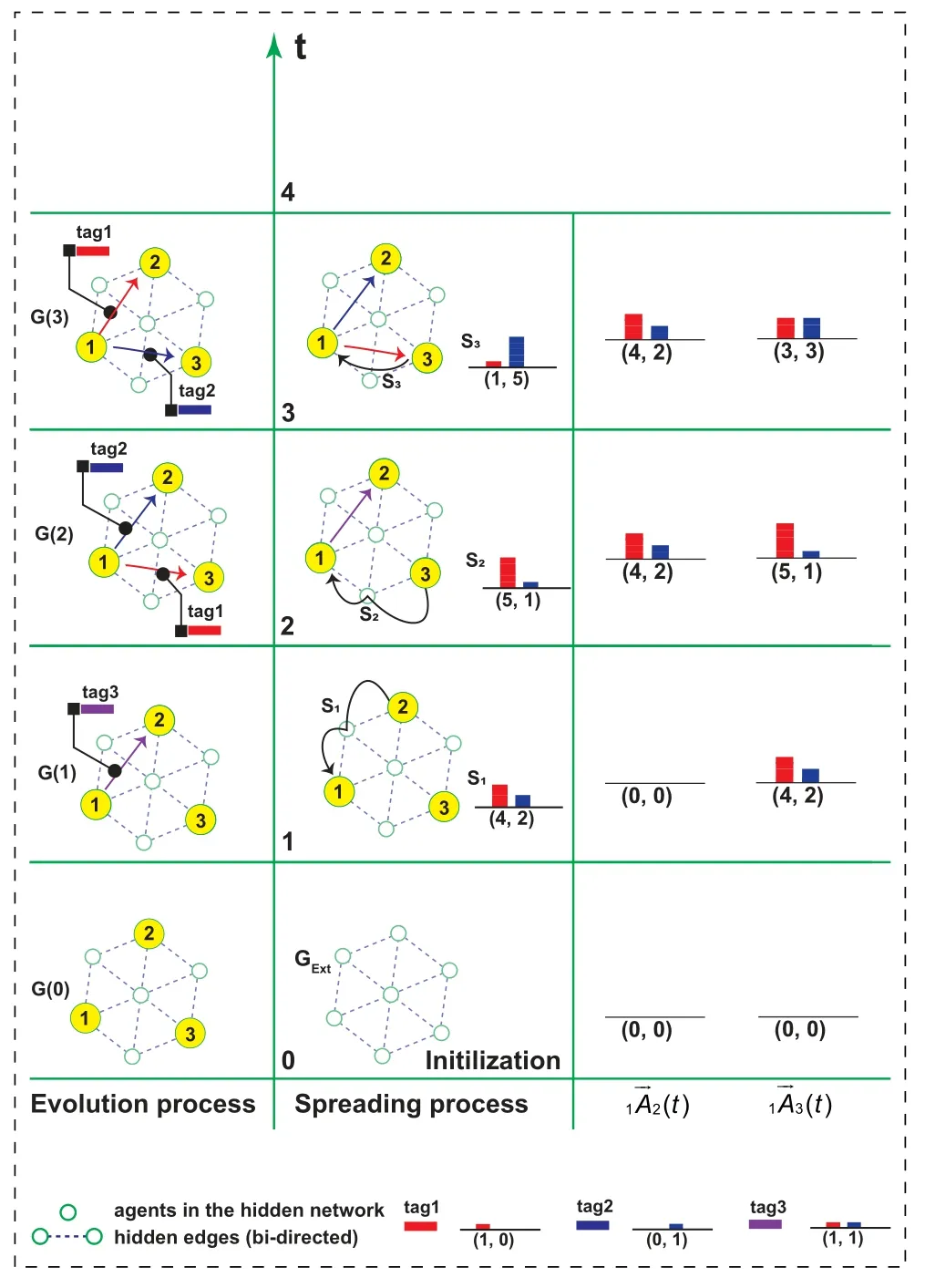
Figure 2.An illustration of the information-driven network evolution process.
where the optimization variableY= (0,Y[2],Y[3])andY[h]∈ {0,1}3forh= 2,3.At the end oft=1,v1adopts the optimal linking strategy by building an out-edge tov2with a tag set{tag3}.After that,timetincreases by one.Att= 2,v3is activated,and she suppliesv1with a randomly generated signals2= (5,1).By solving the updated optimization problem,v1tunes her/his linking strategy tov2fromX1,2(1)=tag3 toX1,2(2)=tag2,and then builds an out-edge with a tag set{tag1}tov3.At timet= 3,v3is activated again.This time,v3directly sendsv1a random signals3.After updating the database,v1’s optimizer suggests her/him to adopt the reverse optimal linking strategy.Finally,the network evolves into G(3).
IV.CONNECTING TO THE DE MODEL
In the DE model,trefers to the time.Notationst<0,t=0 andt>0 are used to denote the past,the present and the future,respectively.At the present time(i.e.t= 0),the DE model initialize G = G(0) to be an arbitrary network withnnodes andmedges with labels inC,whereC={C1,C2,···,Ch}represents all the labels that can be observed in the whole course of G’s changing process.Let G(t) = (V(t),E(t)) be a temporal network withV(t) ={v1,v2,···,vn},for timet=−∞,···,−1,0,1,···,+∞.For an edgevi →vjin G(t),notationC(i,j,t)is employed to denote the label set associated with it.It is assumed that every edge in networks should be assigned at least one label.Therefore,there exists an edge fromvitovjat timetif and only ifC(i,j,t)≠∅.
Regarding edges with the same label in G as the components of a layer of network G,we can divide G intohdifferent layers.Specifically,thel-th layer of G(t),denoted by Gl(t) = (Vl(t),El(t)),is defined to be the subnetwork consisting of all the edges inE(t)with labelCland all the nodes involved in these edges(see Figure 1a in[21]).For nodevi,define its potential energy with respect to thel-th layer at timetto be
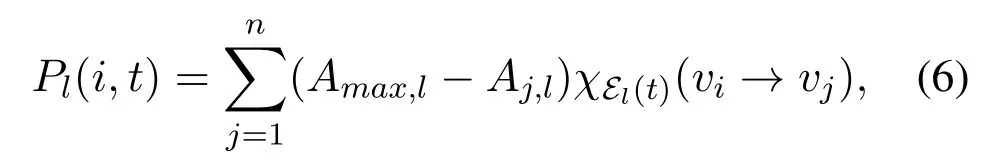
whereAmax,l= maxvi∈V Ai,landχEl(t)(vi →vj) =1 ifvi →vj ∈El(t); otherwiseχEl(t)(vi →vj) = 0.The value ofPl(i,t)describes how eager nodeviis to rewire its out-edges in Gl(t)to connect to nodes with higherl-attractiveness at timet(see Figure 1a).Further,definevi’s potential energy and the system’s potential energy at timetto beandrespectively.A node’s higher potential energy means the stronger desire for this node to rewire its out-edges,and the higher potential energy of a system indicates a more structurally unstable state of this system.
There exists an evolution mechanism in the DE model: at each timet >0,a node rewires one of its out-edges in a layer of G(t)and then timetincreases by 1,such thatP(G,t+1)≤P(G,t)(see Figure 1c in[21]).In addition,there exists a degradation mechanism: at each timet <0,a node rewires one of its out-edges in a layer of G(t)and then timetdecreases by 1,such thatP(G,t −1)≥P(G,t)(see Figure 1b in[21]).
Theorem 1.The DE model defined above is a particular case of the proposed NFF.
V.CONCLUSION
In this paper,we propose an IDN framework that enables us to embed a complex network into a communication network of multiple intelligent agents.We prove that the NFF extends the DE model showing that the IDN framework can tackle a crucial but unsolved problem,i.e.,the PUIT detection problem in networks outside the scope of the DE model.As a practical application,this theoretical finding illuminates that our framework enables engineers to discover the hidden features of users of communication networks and help them to design communication systems providing users better experience.
Moreover,the proposed approach suggests exciting research avenues for researchers in information and communications engineering,network scientists,and data analysts.For future research in knowledge discovery,interpreting the observed data in terms of an intelligent agents’ communication network may lead to new sets of results in data mining and knowledge discovery in network data.Future research in network science may explore additional applications of the proposed communication network approach beyond those developed here,including network structure analysis [26],layer detection [2],link prediction [19,25],ranking algorithms [27],and recommender systems[22,28].
In conclusion,we hope our proposed IDN-based communication network approach would facilitate network data analysis and sciences related to networks as the well-studied complex network approach does.
ACKNOWLEDGEMENT
We would like to thank Lixia Xiao,Daiming Qu,Linyuan L¨u and the anonymous referees for their suggestions which greatly improved this article.This work was supported in part by Young Elite Scientists Sponsorship Program by CAST under Grant number 2018QNRC001,and National Science Foundation of China with Grant number 91738202,62071194.
APPENDICES
Appendix A:Basic Notations
For a vectorXitsh-th element is denoted byX[h]or[X][h].We always use G to denote a network.NotationsV(G)andE(G)are employed to represent the agent set and the edge set of G,respectively.Letebe a directed edge inE(G).We use notationsandto denote the source agent and the target agent ofe,respectively.Multisets are containers that store elements following a specific order,and where multiple elements can have equivalent values.LetAbe a multiset,we defineχA(x) = 1 ifx ∈A,otherwiseχA(x) = 0.LetA={S1,S2,···,Sn1}andB={S′1,S′2,···,S′n2}be two multisets,we defineA+Bto be the multiset consisting ofn1+n2elements,where theh-th elementS′′his
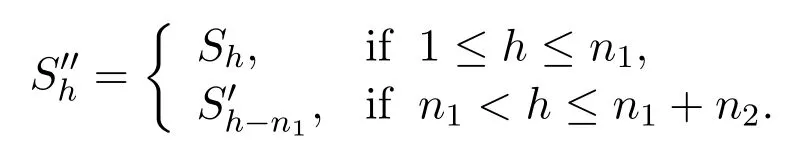
The following table summarizes all the frequentlyused notations throughout this paper.
Appendix B:Information Supply of Intelligent Agents
LetC1andC2be two information topics.We assume that (1) agentvideems that agentvjcan produceIh-type information at timetif and only if there existsS ∈ Si,j(t),such thatIh ≤sign(S),forh= 1,2,···,M; (2) if agentvideems that agentvjcan produce bothC1-type andC2-type information,then agentvibelievesvjcan produce information of sign(C1+C2)-type(i.e.,(C1∨C2)-type.See the definition of operator“∨”at the end of Section II).Based on the first assumption,we have at timet,all the primitive topics deemed byvithatvjcan produce compose the following set
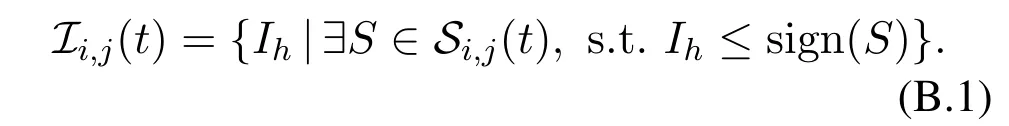
Let|Ii,j(t)|=sandIi,j(t) ={J1,J2,···,Js}.By Eq.(B.1),there existsSg ∈ Si,j(t) such thatJg ≤sign(Sg),forg= 1,2,···,s.On the one hand,we have sign[∨Ii,j(t)]= sign(J1∨J2∨···∨Js)≤sign(S1∨S2∨···∨Ss)≤sign[∨Si,j(t)].On the other hand,forw ∈{1,2,···,M}ifIw·sign[∨Si,j(t)]=1(where operator“·”refers to the inner product of vectors),then there existsS′w ∈Si,j(t) such thatIw ≤sign(S′w).By Eq.(B.1),one hasIw ∈Ii,j(t).Therefore,Then we have
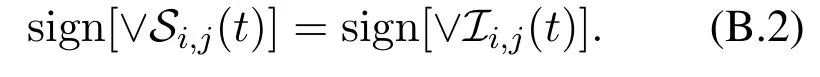
It follows the above two assumptions thatvideemsvjcan produceC-type information,if and only if there existsag ∈{0,1}forg=1,2,···,s,such that


Table 1.Frequently-used notations in this paper.
Appendix C: Objective Function of the Optimization Problem
We assume the composite response to multiple pieces of information in a signal respects the superposition principle.LetS ∈S,i ∈{1,2,···,N}andChbe a nonzero tag inC,forh= 1,2,···,s.According to the superposition principle,we define
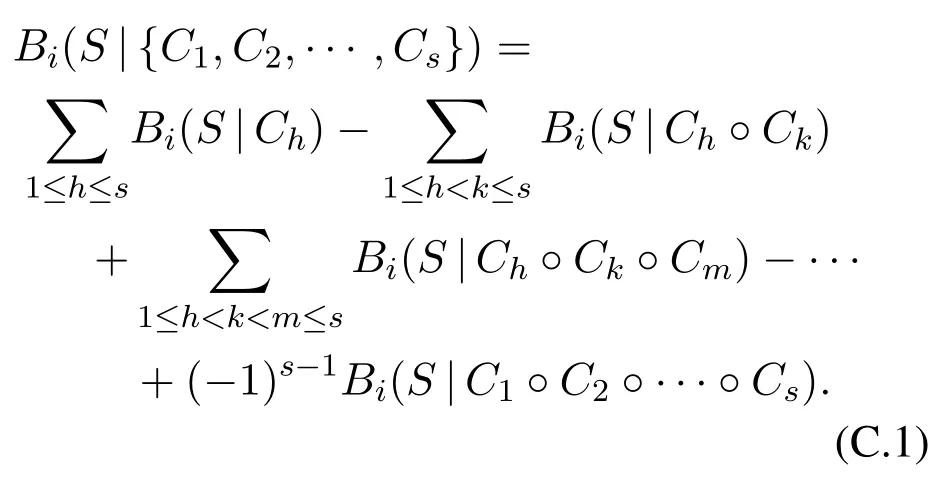
LetC ∈C.According to the principles for response models introduced in Section II and Eq.(C.1),we haveBi(S|I) =Mh=1Bi(S|Ih).DenoteBi(S|Ih)asBi(S,h) forh= 1,2,···,M,and=Then we obtainBi(S|C) =Therefore,
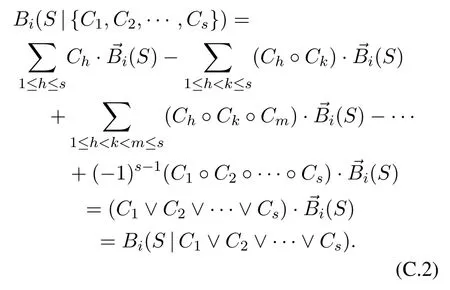
Let agentvi’s linking strategies at timetcompose a vector(t) = (Xi,1(t),Xi,2(t),···,Xi,N(t)).LetXi,j(t) =∨Xi,j(t),forj= 1,2,···,N,andXi(t) = (Xi,1(t),Xi,2(t),···,Xi,N(t)).It follows Eq.(C.2) thatBi(S|Xi,j(t)) =Bi(S| ∨Xi,j(t)) =[∨Xi,j(t)]· →Bi(S)=Xi,j(t)· →Bi(S).Therefore,when|Si,j(t)|>0,we have
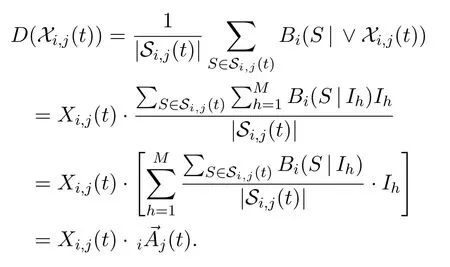
When|Si,j(t)|= 0,we have= 0 andD(Xi,j(t)) = 0.ThenD(Xi,j(t)) =Xi,j(t)Combining the two cases,we obtainD(Xi,j(t)) =Then the objective function of the optimization problem can be rewritten as

Appendix D: Dynamic Supply-demand Constraints
Letvi’s linking strategy tovjat timetbeXi,j(t) =∨Xi,j(t) andXi,j(t) ={C1,C2,···,Cs},where integersis no less than one,andCh ∈ Cforh=1,2,···,s.On the one hand,Ch ∈Xi,j(t) implies thatviseeksCh-type information generated byvjat timet,forh= 1,2,···,s.In other words,vibelievesvjcan generateCh-type information,forh=1,2,···,s.According to Eq.(4),Ch ≤sign((t)),forh=1,2,···,s.Then we have
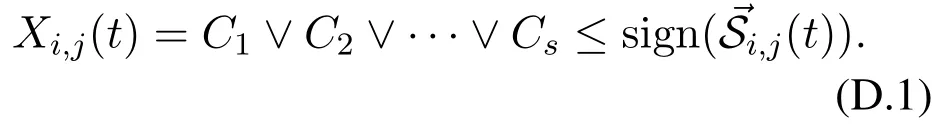
On the other hand,according to Eq.(3),we require
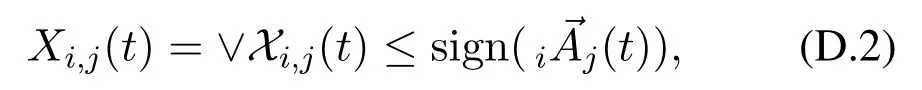
fori= 1,2,···,Nandj= 1,2,···,N,to avoid useless demands.Assume sign(iAj(h,t)) = 1.Then we have0.Thus,there existsS′ ∈ Si,j(t) such thatBi(S′|Ih) =Bi(S′ ◦Ih)>0.According to the first principle for response models,we have S′◦Ih≠ 0.Therefore,sign(→Si,j(t)) ≥sign(S′) ≥Ih= sign(iAj(h,t))Ih.Consequently,we have sign(i→Aj(t)) =Mh=1sign(iAj(h,t))Ih≤sign(→Si,j(t)).This inequation shows that (D.2) implies (D.1).Finally,we call constraint (D.2) the dynamic supply-demand constraint.
Appendix E:Bounded Out-degree Constraints
For agent vi,let ki,out(t)denote its out-degree at time t.We assume the number of out-edges of every agent in the framework is bounded.Specifically,
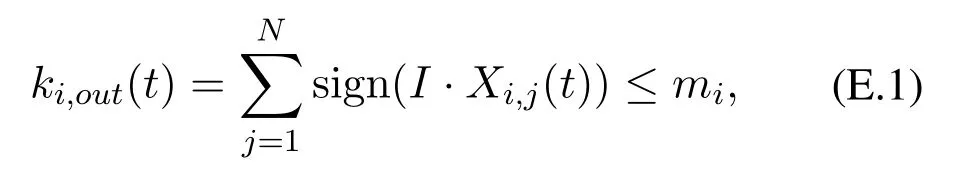
where the non-negative integer miis a feature of agent vi.For a vector X,its h-th entry is denoted by X[h]or[X][h].It follows constraint(E.1)that
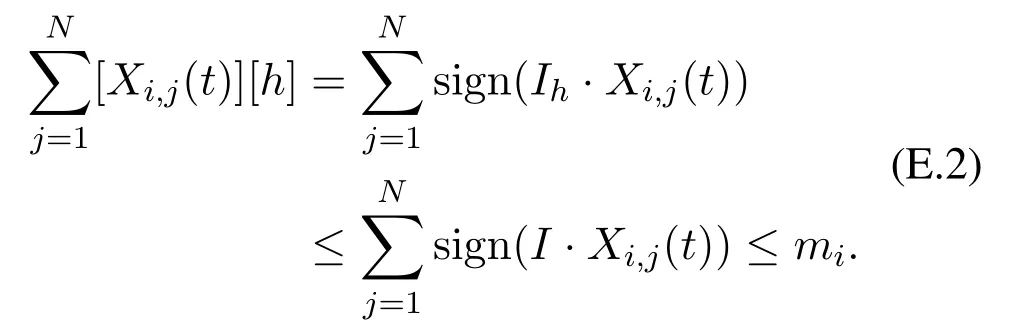

It follows constraint(E.3)that
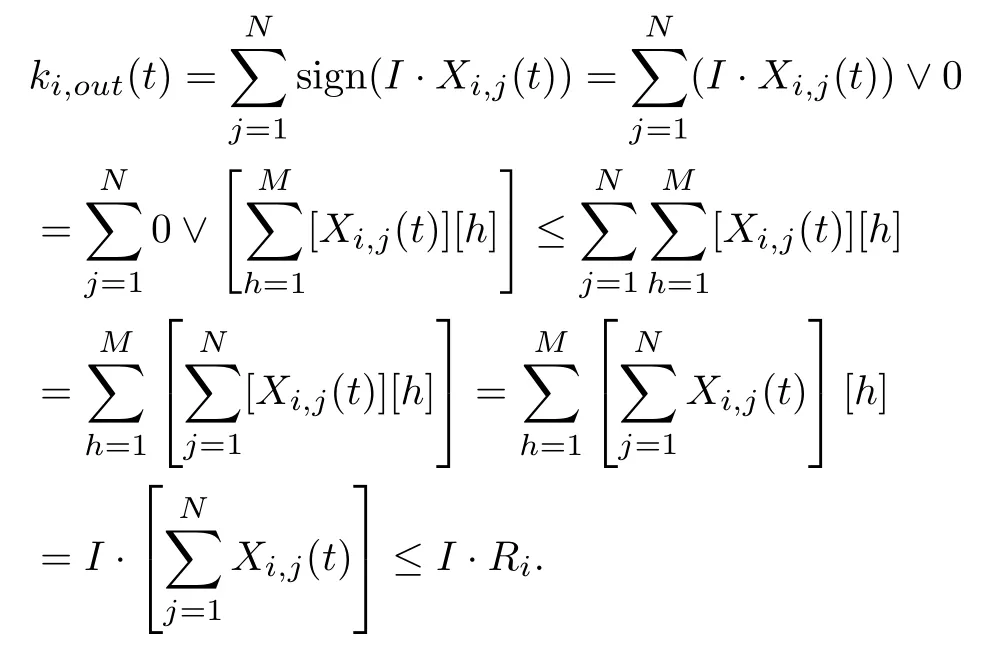
Note that constraint (E.3) implies constraint (E.1)when I ·Ri≤mi.
Appendix F: Sovling the Optimization Problem
LetiQj(t) = sign((t)).Matrix Xi(t) =(Xi,1(t),Xi,2(t),···,Xi,N(t)) is an optimal linking strategy of agent viat time t if it is a solution to the following optimization problem(denoted by P1[i,t]):
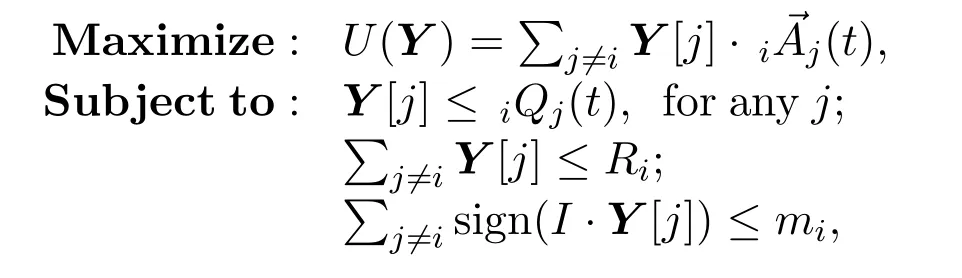
where Y = (Y[1],Y[2],···,Y[N]),Y[i]= 0 and Y[j]∈C for j ≠i.We always set I·Ri=mifor i=1,2,···,N.According to Appendix C in the main text,the last constraintcan be neglected.Solutions to P1[i,t]always exist.The following proposition provides a method to construct a solution to P1[i,t].
Proposition 1.For h = 1,2,···,M,define U(h)(vi) = {vj∈V(G)|iAj(h,t)>0} anddenote a subset of U(h)(vi) consisting of deg(h)(vi)agents with the deg(h)(vi) largest sores of Ih-type information supply abilities observed by viat time t in U(h)(vi).For j =1,2,···,N,let Xj∈C and
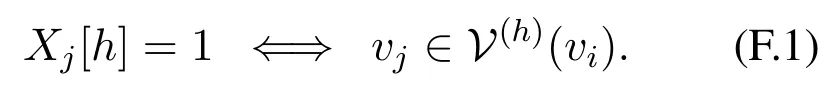
Then X =(X1,X2,···,XN)is a solution to P1[i,t]Proof.(1)We show that X satisfies all the constraints in P1[i,t].Then,we have

AssumeXj[h]= 1.By Eq.(F.1),we havevj ∈V(h)(vi).Consequently,iA(h,t)>0,and then sign(iAj(h,t))=Xj[h].For anyj,we have
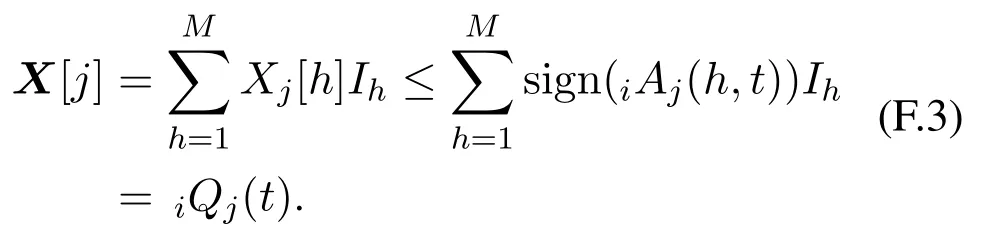
Eqs.(F.2)and(F.3)imply thatXsatisfies all the constraints in P1[i,t].
(2) We showU(X′)≤ U(X) for anyX′which satisfies the constraints in P1[i,t].LetX′= (X′1,X′2,···,X′N) andV′(h)(vi) ={vj ∈U(h)(vi)|X′j[h]= 1}.By the bounded outdegree constraint,we havefor anyh.Then we have for anyh,|V′(h)(vi)| ≤min{Ri[h],|U(h)(vi)|}.Thus,for anyh,|V′(h)(vi)|≤deg(h)(vi) =|V(h)(vi)|.Recall the definition ofX,we have for anyh,Therefore,for anyh
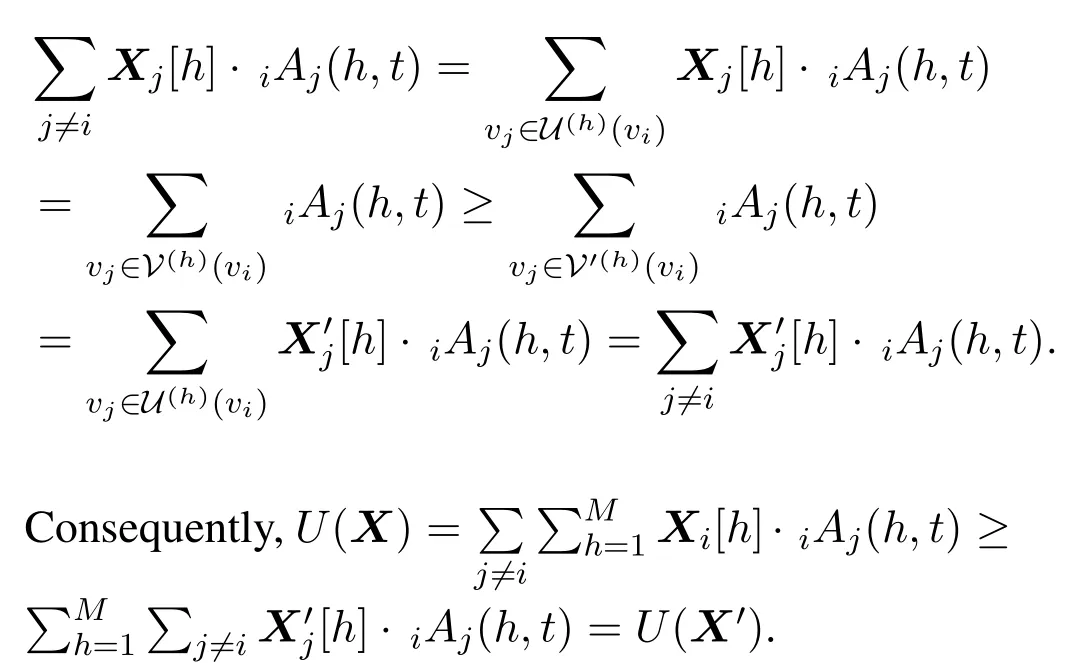
To sum up,we haveXis a solution the P1[i,t].
Appendix G:Proof of Theorem 1
Lemma 1.Let n and M be two positive integers,Il be an(M+ 1)-dimensional vector for l=1,2,···,M+1,and{0,1,n+ 1},h ∈ {1,2,···,M}}.Let A={S1,S2,···,S|A|} denote a multiset of some nonzero signals in S and h ∈{1,2,···,M}.DefineLet h′ be a given inte-ger in {1,2,···,M},h be an arbitrary integer in{1,2,···,M} with h′≠h,and S′ be a given multiset of non-zero signals in S.Then for an interval(β1,β2)with0< β1< β2< n+ 1,there ex-ists a non-empty multiset S′′ of signals in S such that αh′(S′+S′′)∈(β1,β2)and αh(S′+S′′)=αh(S′).Proof.For a signalS ∈ Sand an integerh ∈{1,2,···,M},defineψh,x(S) to be a vector whoseh-th element isxandh′-th (h′≠h) element isS[h′].Further,for a multiset of signalsA={S1,S2,···,S|A|},we defineψh,x(A) to be{ψh,x(S1),ψh,x(S2),···,ψh,x(S|A|)}.Note that for any signalSinSandh ∈{1,2,···,M},ψh,0(S)is non-zero sinceψh,0(S)≥IM+1.
(1)Case 1:αh′(S′)> β2> β1>0.There exists two positive integerspandqwithq > psuch thatαh′(S′)· p/q ∈(β1,β2).LetS′′=
Then we have

and forh ∈{1,2,···,M}withh≠h′
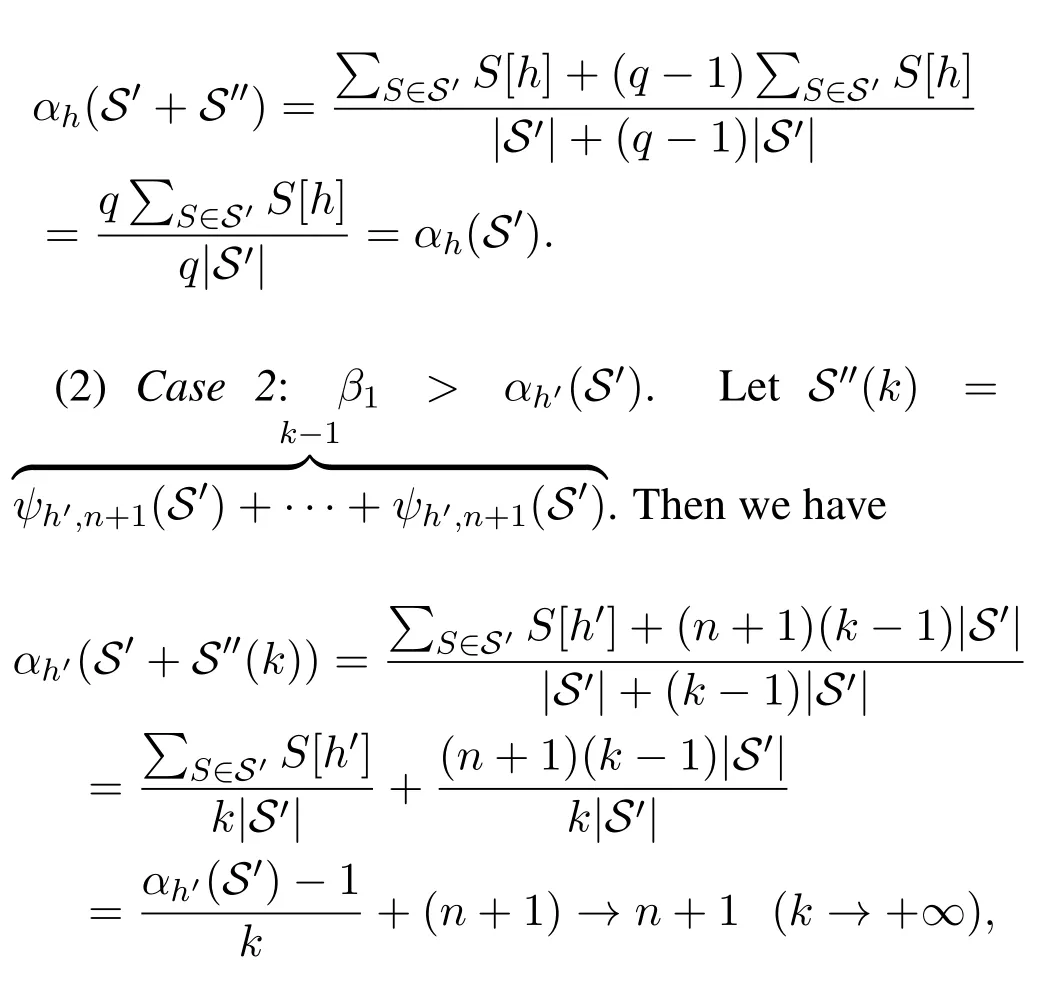
and forh ∈{1,2,···,M}withh≠h′
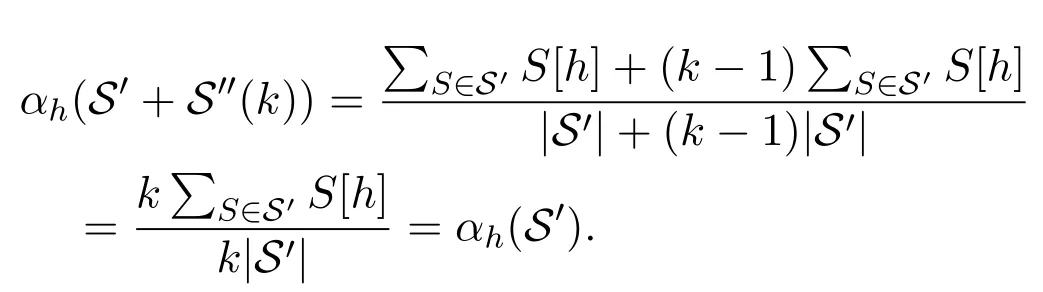
Thus,there exists a large enoughk′such thatβ1<αh′(S′+S′′(k)) (3) According toCase 2,there existsS′′1such thatαh′(S′+S′′1)∈(β2,n+1)andαh(S′+S′′1)=αh(S′)forh ∈{1,2,···,M}withh≠h′.Then byCase 1,there existsS′′2such thatαh′(S′+S′′1+S′′2)∈(β1,β2) andαh(S′+S′′1+S′′2) =αh(S′+S′′1) forh ∈{1,2,···,M}withh≠h′.LetS′′=S′′1+S′′2.Finally,αh′(S′+S′′)∈(β1,β2)andαh(S′+S′′) =αh(S′)forh ∈{1,2,···,M}withh≠h′. (1) Letv1,v2,···,vnbe all the nodes in G(t)fort=−N1,−N1+ 1,···,N1.Assume thatC1,C2,···,CMare all the different labels observed inLetIlbe an(M+1)-dimensional vector forl= 1,2,···,M+1,andChcorrespond toIhforh=1,2,···,M.According to the DE model,we assume without loss of generality that: a)1≤Ai,h ≤nfor anyi= 1,2,···,nandh= 1,2,···,M; b)Ai,h≠Aj,hfor any 1≤i≠j ≤nand 1≤h ≤M.For each agent (node)viin G′(t′),its signal generator is defined to beqi=(Oi,1,Oi,2,···,Oi,M),whereOi,his a binomial distribution.Setsi,h ~Oi,h.Then and E(si,h) =Ai,hIh.Here,P(•) and E(•) denote the probability and expectation.For each nodeviwith 1≤i ≤n,we assume that each signal it can generate belongs to{0,1,n+1},h ∈{1,2,···,M}}. (2) For each nodeviwith 1≤i ≤n,we assign it a signal processorBi(•).Specifically,for a signalSgenerated by a node inandh= 1,2,···,M,defineBi(S|Ih) =S·Ih=S[h].Then according to Section II,we have for agentsviandvj (3) For each nodeviwith 1≤i ≤n,letRi[h]= (4) Letv0be a node which is not in{vi}ni=1.Let G′Hidbe a directed fully-connected network consisting ofn+ 1 agents,i.e.,v0,v1,v2,···,vn.Att′= 0,we construct G′(0)by addingv1,v2,···,vnto it.At the beginning,it is obvious thatE(G′(0)) =∅andSi,j(0)=∅for 1≤i,j ≤n. (5) Forh= 1,2,···,M,letbe all the edges carrying labelChin G(−N1),wheren(h)is a function whose value is the number of edges with labelChin G(−N1).Letn(0) = 0 andh= 1.At timet′with0< t′ ≤ n(1),agentgenerates a randomly signalSt′ ∈{Ih,(n+ 1)Ih}and sends it toandThen according to Section II,we haveit′Ajt′(h,t′) =St′[h]≥1.Lethrun through 1,2,···,MandThen at timet′=t0,we have for each agentviandh′ ∈{1,2,···,M},{j=1,2,···,n| iAj(h′,t0)>0}={j= 1,2,···,n|Ch ∈Ci,j,0}.Then according to Proposition 1,we have G′(t0)=G(−N1). (6) In G′(t′),let=min{iAj(h,t′)|[Xi,j(t)][h]=1}and=max{iAj(h,t′)|[Xi,j(t)]=0},where 1≤i,j ≤nandh= 1,2···,M.According to the NFF (see the main text),we can assume that for anyiandIn the transition from G(−N1) to G(−N1+ 1),we assume without loss of generality that nodev1removes a labelCh′onv1→ v2and re-allocatesCh′to another directed edgev1→v3.Note thatThen by Lemma 1,there exists a sequence of signals{St0,1,St0,2,···,St0,m1(1)}inS(G′),such that and for anyh≠h′ Fort′′= 1,2,···,m1(1),let agentv2generate signalSt0,t′′att′=t0+t′′and send it to agentv1.By the above two equations,we have1A2(h,t0+m1(1)) =1A2(h,t0) for anyh≠h′,andiAj(h,t0+m1(1)) =iAj(h,t0) for anyh ∈{1,2,···,M},i≠ 1 andj≠ 2.According to Proposition 1,we know that no changes will happen in the evolution process fromt′=t0tot′1=t0+m1(1).Note thatBy Lemma 1 again,there exists a sequence of signalsinS(G′),such that and for anyh≠h′ Fort′′′= 1,2,···,m2(1),let agentv3generate signalS′t0,t′′′att′=t′1+t′′′and send it to agentv1.Combining the two aspects above,we have1A3(h,t′1+m2(1)) =1A3(h,t′1) for anyh≠h′,andiAj(h,t′1+m2(1)) =iAj(h,t′1) for anyh ∈{1,2,···,M}andi≠1 andj≠3. LetX1= (X1,1,X1,2,...,X1,n) be the optimal linking strategy of nodev1at timet0.LetY=(Y1,Y2,···,Yn)and According to Proposition 1,we know thatYis the optimal linking strategy at timet′=t′1+m2(1).Therefore,we have G′(t1) = G(−N1+ 1) wheret1=t′1+m2(1). (7) In the same way,we gett2,t3,···,t2N1with G′(tk)=G(−N1+k)fork=1,2,···,2N1. Above all,we conclude that any instance of the DE model,can be seen as a sub-sequence of an instance of the proposed NFF.
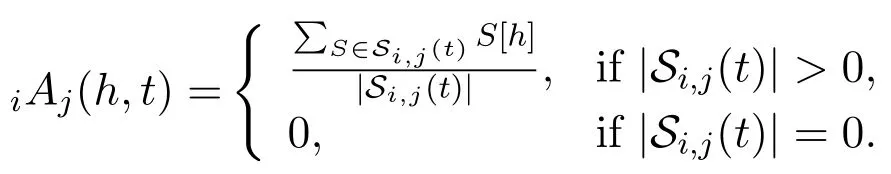
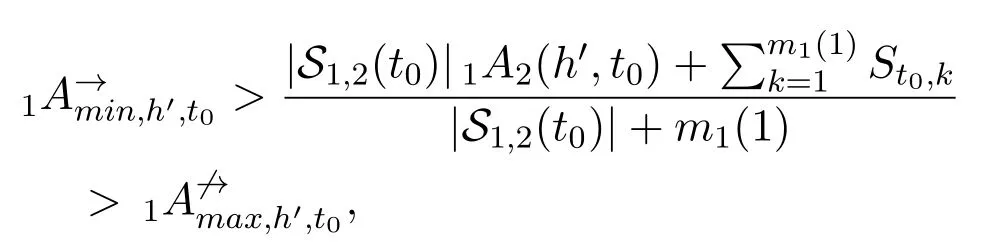
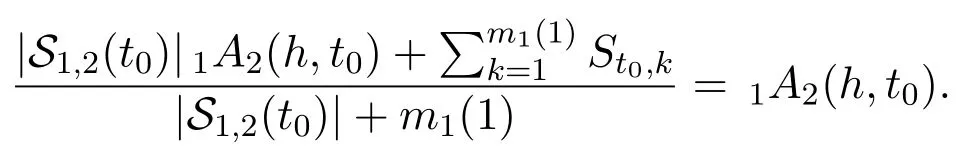
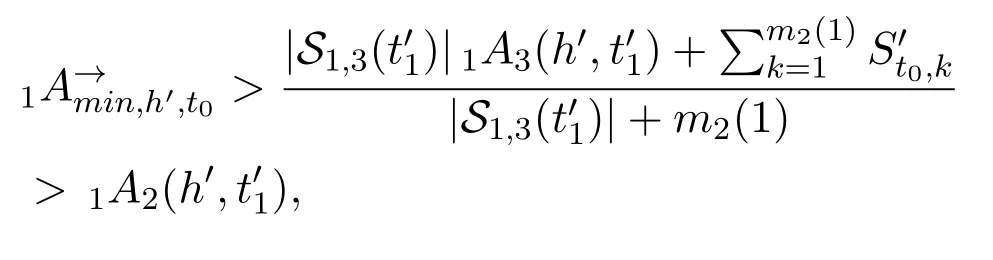
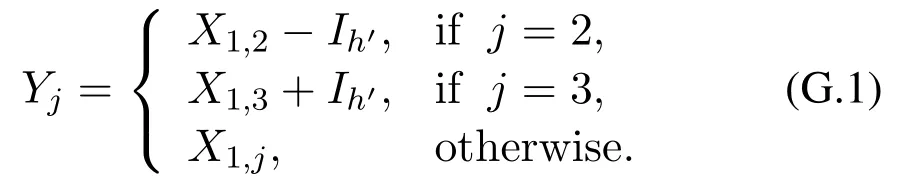
- China Communications的其它文章
- Joint Topology Construction and Power Adjustment for UAV Networks: A Deep Reinforcement Learning Based Approach
- Energy Model for UAV Communications: Experimental Validation and Model Generalization
- Joint Computing and Communication Resource Allocation for Satellite Communication Networks with Edge Computing
- An Intelligent Scheme for Slot Reservation in Vehicular Ad Hoc Networks
- CLORKE-SFS:Certificateless One-Round Key Exchange Protocol with Strong Forward Security in Limited Communication Scenarios
- Deep Learning Based User Grouping for FD-MIMO Systems Exploiting Statistical Channel State Information

