椭圆型方程系数识别问题正则化解的收敛速度

王 谦， 何 琴

(兰州交通大学 数理学院， 甘肃 兰州 730070)

椭圆型偏微分方程是用于描述物理平衡稳定状态的一类方程[1]。偏微分方程的正问题是由已知方程的定解条件求定解问题的解，而反问题[2]是由部分已知信息求定解问题中的某些未知量。由于大部分反问题是不适定的，正则化方法就成为解反问题的主要工具[3-6]。虽然有许多学者致力于研究正则化方法，但很少研究正则化解的收敛速度[7-10]。

本文研究了椭圆型方程的系数识别问题，考虑如下椭圆型方程Dirichlet问题：

-div(q∇u)+c(x)u=finΩ，

(1)

u=0 on ∂Ω。

(2)

其中：q是未知系数，利用u在Ω上的观测值来反演q。将Tikhonov正则化应用于新的凸能量泛函Jzδ， 并求出其解的收敛速度。 对于凸能量泛函的设定是处理该问题的难点， 既要保证泛函的凸性， 又要易于求解收敛速度。

通过多次检验， 构造如下泛函：

(3)

其中：ρ>0 是正则化参数，q*是q的先验估计。

本文的主要贡献：证明了泛函(3)的严格凸性，从而在容许集内极小化问题有唯一解；提出了形式上相对简单的源条件，进而证明了最优解的收敛性，并给出了收敛阶。

1 反问题设置

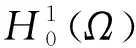
成立，则称u为问题(1)和问题(2)的弱解。如果系数q属于下列集合

(4)

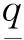
(5)

(6)

其中：

(7)

且CΩ是一个仅依赖于区域Ω的常数。在Poincaré-Friedrichs不等式中，有

(8)

2 Tikhonov 正则化

(9)

其中：δ>0。于是问题转变为由zδ重构q。为了解决问题，在集合Q上最小化凸泛函是

(10)

由于问题是不适定的，使用稳定的Tikhonov正则化方法求解它，即解决最小化问题

(11)

在证明之前，先引入q*最小范数解的概念，以及U(q)的一些性质。

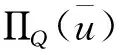
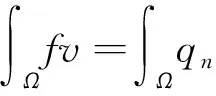
(12)

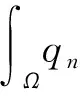
(13)

引理证毕。

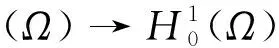
-div(q∇η)+c(x)η=div(h∇U(q)) inΩ，η=0 on ∂Ω

(14)

此外， 对于所有h∈L∞(Ω)， 有

(15)

(16)

其中:α由式(7)定义， 且α>0。 对于任何h∈L∞(Ω)， 根据Lax-Milgram引理， 得到变分方程

(17)

(18)

由不等式(18)和不等式(14)， 得到

(19)

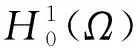
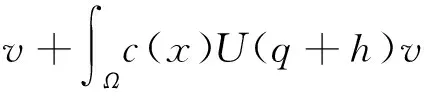
成立。 因此，

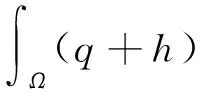
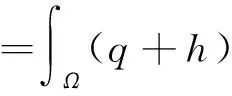
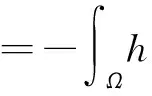
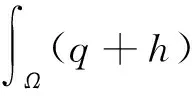
令v=U(q+h)-U(q)-η，由等式(16),得到

α‖U(q+h)-U(q)-η‖H1(Ω)≤‖h‖L∞(Ω)‖η‖H1(Ω)。

(20)

由不等式(19)和不等式(20)，得

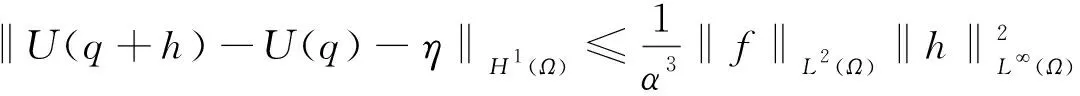
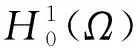
引理证毕。

引理3 由式(9)定义的泛函Jzδ(q)在凸集Q上是凸的。

证明：对所有q∈Q和h∈L∞(Ω)有

(21)

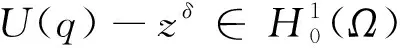
那么，对所有的q∈Q和h,k∈L∞(Ω)，Jzδ的二阶Fréchet导数为

因此， 根据式(5)， 对所有q∈Q和h∈L∞(Ω)有

即泛函Jzδ(q)在集合Q上是凸的。

引理证毕。

证明：首先，证明泛函Jzδ(q)在集合Q上关于L2(Ω)-范数是连续的。

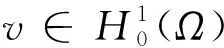
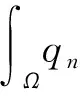
(22)

根据不等式(15)，得

(23)

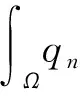
(24)

根据{qn}在L2(Ω)-范数下收敛于q和式(23)，当n→∞时，方程(24)右边第一项趋近于零。另一方面，由于{U(qn)}在H1(Ω)内弱收敛趋于θ，当n→∞时，得到

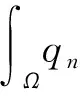
(25)

结合式(22)和式(25)，断定θ=U(q)。

现在证明当n→∞时， 有Jzδ(qn)→Jzδ(q)。由方程(3)得

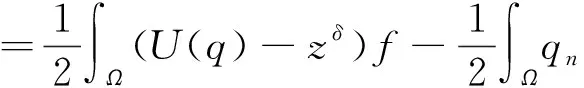
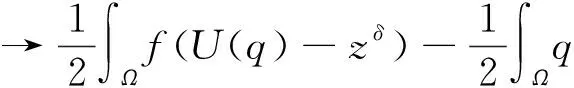
=Jzδ(q)。

定理证毕。

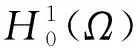
证明：由{qn}的定义，对每个q∈Q，有

(26)

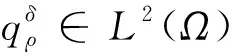
(27)

和

(28)

另外，

(29)

当n→∞时，因为{zn}在H1(Ω)中收敛于zδ，所以右边两个括号中的项趋于零。因此，

(30)

根据式(27)～式(29)，对任意q∈Q有

(31)

(32)

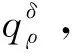
(33)

(34)

联立式(34)和式(30)， 以及不等式(32)有

这与式(27)矛盾。

定理证毕。

3 收敛速度

由于L∞(Ω)=L1(Ω)*⊂L∞(Ω)*，那么对任意q∈L∞(Ω)，有q∈L∞(Ω)*。 对所有h∈L∞(Ω)有

(35)

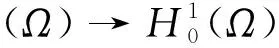
即对所有ω*∈H-1(Ω)和h∈L∞(Ω)有

(36)

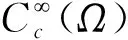
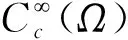
-div(q∇φρ)+c(x)φρ=ψρ-ΔψρinΩ,φρ=0 on ∂Ω。

(37)

(38)

设v=φρ，由集合Q的定义，有

由Cauchy-Schwarz不等式，可得

于是

(39)

根据假设存在一个常数K1>0，对所有ρ∈(0,1)有

(40)

由式(39)和式(40)，对所有ρ∈(0,1)有

(41)

由不等式(41)与Poincaré-Friedrichs不等式，得到式(38)。

引理证毕。

定理3 假设存在一个函数ω*∈H-1(Ω)使得

qχ-q*=U′(qχ)*ω*。

(42)

则，当ρ→0和ρ～δ时，有

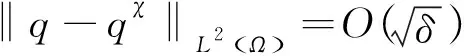
证明：根据正则化解的定义，得到

因此

(43)

(44)

对式(42)的第二项，由式(35)和式(42)，得

(45)

由式(36)和式(45)可得

(46)

(47)

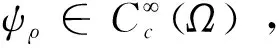
‖ω-ψρ‖H1(Ω)≤ρ。

(48)

考虑下列椭圆型方程的Dirichlet问题：

-div(qχ∇φρ)+c(x)φρ=ψρ-ΔψρinΩ，

(49)

φρ=0 on ∂Ω。

(50)

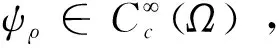
(51)

(52)

(53)

由不等式(35)和式(53)， 得到

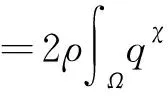
(54)

应用不等式(36)和式(43)，有

(55)

根据式(13)和集合Q的定义， 有

(56)

由式(3)和式(12)，得

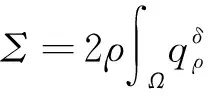
根据式(9)， 得

利用Cauchy-schwarz不等式， 有

(57)

由式(53)～式(55)得到

(58)

根据集合Q的定义和Poincaré-Friedrichs不等式(8)，有

(59)

结合不等式(32)、不等式(33)、不等式(58)和不等式(59)，可得

(60)

由式(58)， {ψρ}ρ∈(0,1)在H1(Ω)-范数下有界和引理2， 存在一个仅依赖于Ω的常数K>0， 使得对所有ρ∈(0,1)， 有

(61)

由式(60)和式(61)得到， 当δ→0和ρ～δ， 有

定理证毕。