基于Radon变换和能量曲线的机织物密度检测

彭 然 胡立文 邓中民

（武汉纺织大学，湖北武汉，430200）

针对生产中机织物经密纬密测量以人工为主费时费力的问题，国内外不少专家学者提出了用计算机图像处理技术来高效、简化并准确地完成这项工作。前期大多数关于机织物经密纬密计算机自动测量研究采用的是快速傅里叶变换的方法。如利用傅里叶变换提取经纱纬纱的空间频率信息测量织物密度［1］；对织物图像进行FFT变换求出频谱，分析频谱强度和分布，计算条纹分布和周期，从而得到经密纬密［2］。而后在传统傅里叶变换的基础上继承和发展产生了小波变换。如用小波变换对机织物图像进行多层离散小波分解和单层信号重构，分别求出重构后图像沿经纬纱线方向的亮度平均值，根据亮度信号求出其周期，进而求出织物的经密纬密［3］；研究了相关系数法在最佳重构层次选择中的作用，提出预处理后进行小波变换，并运用数学形态学进行修正，最终平滑处理成条纹自动计数，计算经密纬密的方式［4］。

在进行实践研究时发现，之前的研究方法存在可以改进的地方。一是图像拍摄过程中织物倾斜导致因角度误差带来的精度影响使计算结果误差大；二是小波处理时小波最佳分解级数的选择基本是人为确定，需要反复试验，并不能完全实现自动化。针对以上问题本研究提出了一种基于Randon变换和能量曲线，结合小波变换的图像处理方法来实现机织物经密纬密的自动测量。

1 机织物图像预处理

1.1 图像采集

选择10块不同机织物，织物表面纹理清晰且干净无污渍。采集图像时尽量保持织物平整，采取固定的拍摄高度，且在织物的下方放置刻度尺。部分采集的织物图像如图1所示。

图1 织物原图

1.2 Radon变换校正

现今计算机图像处理技术对于织物图像的处理都是建立在织物必须是端正无倾斜的图像前提下的，但是在织物图像采集的过程中，由于拍摄环境、织物摆放、人为操作等因素总是无法避免拍摄的织物图像出现倾斜的情况，而这样会导致计算机处理无法获得准确的织物经向纬向信息，造成最终织物密度计算结果误差大。因此本研究采用Radon变换对织物图像进行校正。

Radon算法是一种通过定方向投影叠加，找到最大投影值时角度，从而确定图像倾斜角度的算法，如图2所示。

图2 定义Radon变换的坐标系统

对f（x，y）的Radon变换Rf（p，θ）定义为沿p和θ定义的直线l的线积分。线积分公式见式（1）。

若函数f（x，y）表示一个未知的密度，对f（x，y）做Radon变换，相当于得到f（x，y）投影后的讯号，可以用Radon反变换投影后的结果，重建原始的密度函数f（x，y），它也是重建断层扫描的数学理论基础。

经Radon变换处理后，可以获取织物倾斜角度，确定好倾斜角度后，经计算机程序将图像自动旋转相应角度，使得机织物经纬纱线保持横平竖直，得到倾斜校正的织物图像。经过Radon变换处理后图像进行了3°的角度旋转得到校正后图像。截取大小为5 cm×5 cm的校正图像保存用于后续处理，注意一定要截取织物部分，若拍摄部分取样不足5 cm则尽量取10整除长度，便于后期经密纬密计算比较。

将校正图像进行预处理转换为灰度图像，再进行平滑去噪处理，并用直方图规范化增加图像对比度，使织物经纬纱线信息更加清晰突出。

2 小波变换处理

2.1 小波变换

小波变换可将二维图像逐层分解得到原图像的低频、垂直高频、水平高频和对角线高频分解图像［5-9］。低频部分可以继续分解，这个过程能一直持续下去；在某一层的垂直高频重构图和水平高频重构图中机织物图像的经纱与纬纱信息将得到最佳保留。小波一级及三级分解图如图3所示。

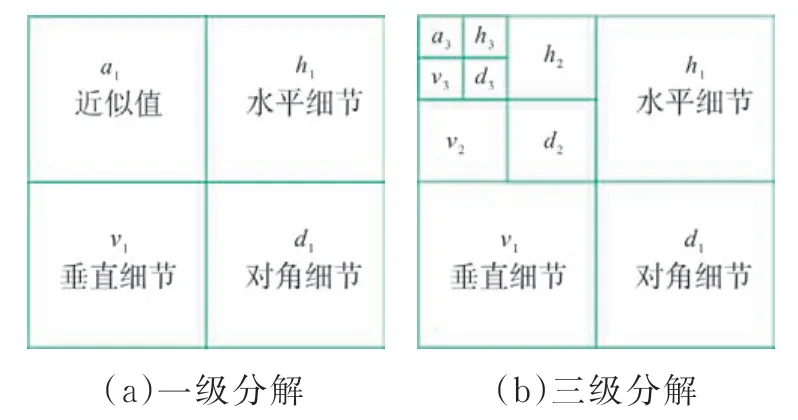
图3 小波一级及三级分解图

机织物是由经纱和纬纱垂直交织而成，图像小波分解得到水平分量和垂直分量基本类似于织物的经向纬向信息，通过处理得到的水平垂直分量即可计算织物的经密纬密。

2.2 能量曲线确定最优分解级数

试验采用wavedec2函数对图像进行多尺度二维小波变换处理，选定小波基函数bio5.5，用该小波对二维信号X（即织物图像）进行N（N=7）层分解，每一层分解分别得到近似分量、水平细节分量、垂直细节分量和对角细节分量。在对织物图像使用小波进行不同层次的分解，得到的水平分量和垂直分量信息完全不同，分量与经纬纱线数目的匹配程度也完全不同。因此小波分解的分解级数直接影响得到的水平垂直分量的数量，也直接影响了图像反映的织物经密纬密准确性，在图像处理的实际操作中需要选择合适的分解级数以得到与经纬纱线图像高度匹配的经纱、纬纱根数信息。同一织物不同层数处理结果如图4所示。

图4 同一织物不同层数处理结果

由图4可以看出，同一织物在同样的处理过程中采用不同的分解级数下得到的分量各不相同，对图中不同层数处理下的分量结果进行计算，在N=3时经密纬密计算结果最为准确，得到分解级数N=3是该织物的最优分解级数。根据对大量织物图片进行不同分解级数处理试验，发现每一块织物都存在一个最优分解级数，并且该最优分解级数与小波变换处理得到的各分量之间存在一定的关系。

由此在确定最佳分解层数时引入能量曲线的概念。即将织物图片小波分解后每层的分量利用w energy函数，采用小波系数平方，然后求和，计算得到各分量的能量占比，最后再归一化，绘制其能量比值曲线。

设定织物图像经N层分解后的近似分量的能量为Es，分解后每层细节分量（包含水平细节分量、垂直细节分量和对角细节分量）的能量为Ed，能量计算公式见式（2）。

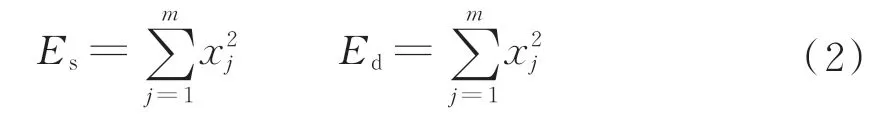
式中：m表示分解后该分量的数据个数，xj表示分解后的每个分量包含的数据（j=1，2，…，m）。经过i层（i=1，2，…，N）分解后的总能量Ez，见式（3）。求出分量的能量占比Di，见式（4）。织物处理后绘制的能量曲线如图5所示。

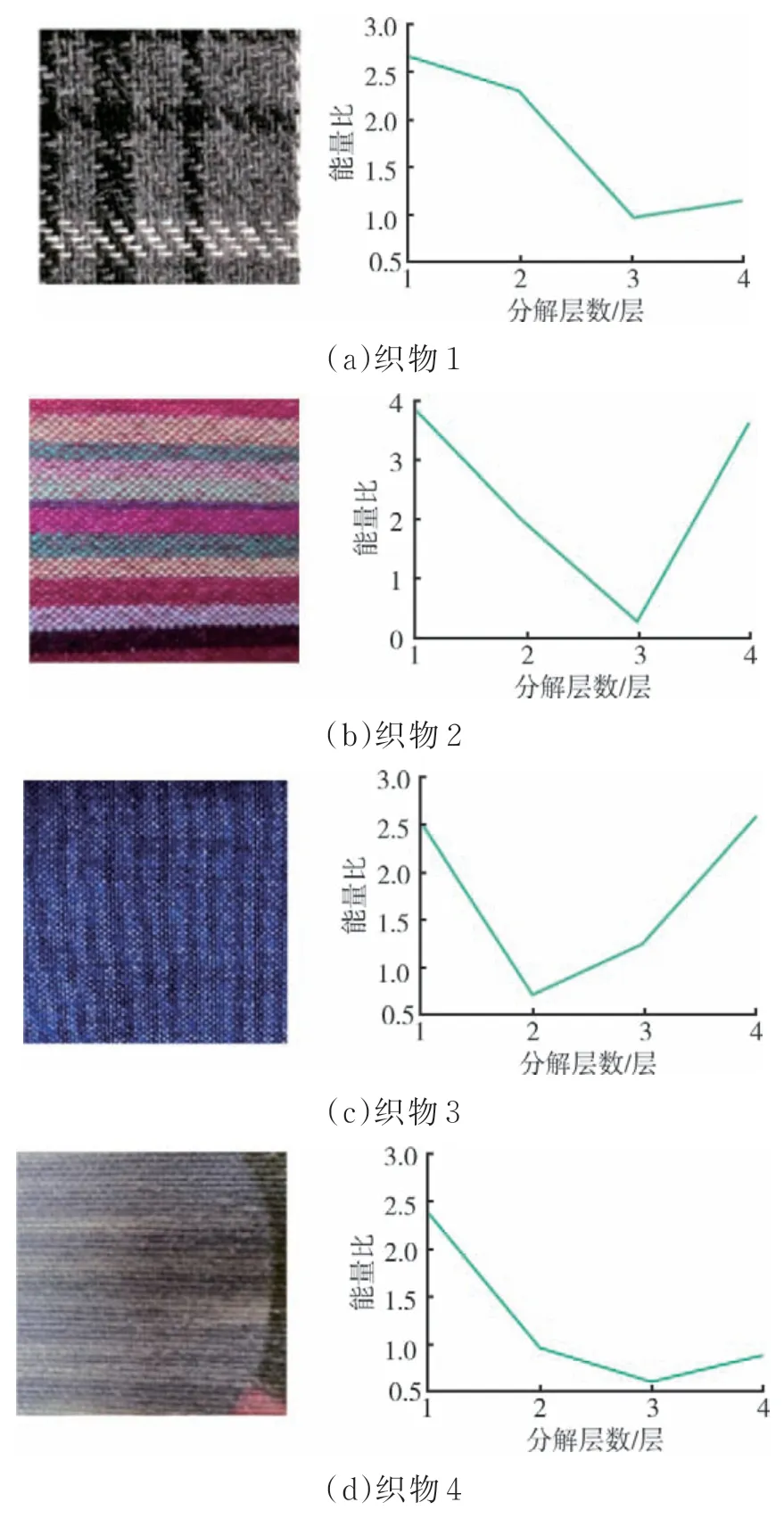
图5 不同织物绘制的能量曲线图

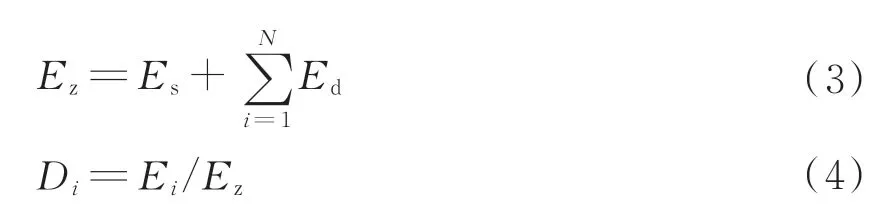
从图5中发现每个能量曲线确实都存在一个最小峰值，为了确定能量曲线的最小峰值是否和小波处理需要的最优分解级数一致，进行了大量的试验比对，最终确定能量曲线最小峰值可以作为织物图像小波分解最优分解级数值来使用。

选取能量曲线最小峰值对织物图像进行小波分解和重构，得到经密纬密计算需要的织物垂直分量图和水平分量图。

2.3 织物重构图优化

小波分解与重构后的垂直分量和水平分量呈现出波浪状，并不能很好表示织物纱线根数信息，这样无法准确计算织物密度，必须进行进一步的处理。不同织物小波处理结果如图6所示。其中，左图为垂直抖动法图像，右图为水平抖动法图像。

图6 不同织物小波处理结果图

本研究采用误差扩散抖动法来实现图像的二值化处理，对重构后的垂直分量和水平分量进行二值化，得到的图像产生黑白交替的像素，且与原来的灰度看起来很接近，既保护了边界，又减少了计算量。

二值化后图像的黑白交替像素排列虽然能看出纱线的排列情况，但不光滑，还含有噪声，且不方便计数，要进行平滑处理。平滑处理的原理是以图像中处于多数的灰度值（0或1）代表这一行或列的具体形态（黑或白），使纱线变直，达到平滑的效果，以方便计算纱线数量［10］。处理结果如图7所示。

图7 各织物分量优化效果

3 机织物经密纬密计算

经过优化处理后得到的水平分量和垂直分量图像，就是与织物高度匹配的经纱纬纱排列，取优化后图像的行或列，计算连续黑色像素的个数除以图像长度（宽度），得到该方向的纱线排列密度（根/像素），根据电脑分辨率（像素/cm）即可计算出机织物密度（根/10 cm）=纱线排列密度×分辨率×10。

运用此程序对选取的10块布样进行测试，并使用照布镜对每块织物进行经密纬密的人工测量，每块织物测得3个数据，然后取其算术平均值为最后人工的测定结果。将测试结果与传统的人工测试进行误差计算。数据比较见表1。

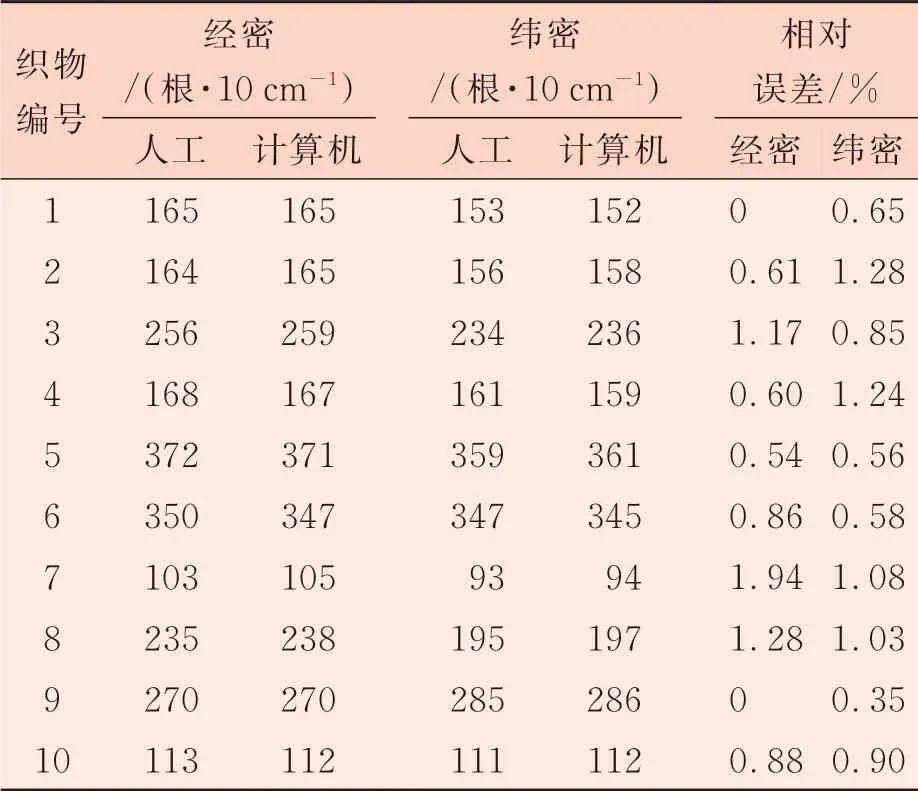
表1 人工测量和计算机测量的数据比较

由表1数据可以看出，计算机程序处理得到的结果和人工测量结果基本一致，织物经密纬密检测的相对误差在1.00%左右，结果较为理想。

4 结语

用计算机图像处理方法测试机织物的经密纬密，相比于传统人工测试处理速度快、效率高、劳动强度小，且计算结果也基本准确。Radon变换校正较好地解决了织物倾斜的问题，能量曲线确定最优分解级数方法的提出，进一步满足了自动准确测量经密纬密的需求，但也有不足之处。试验中发现在处理组织结构复杂的织物，例如多种彩色细条花纹织物、有装饰性花样设计的织物，相对于结构简单或是素色织物来说处理结果不够准确，还需要进一步研究改进。