高温涡轮交叉肋冷却通道的流动换热特性研究

白 超,郭兆元

(1.中国船舶重工集团公司第705研究所,陕西 西安 710077;2.哈尔滨工程大学 动力与能源学院，黑龙江 哈尔滨 150001)

目前先进的燃气涡轮机涡轮前入口温度已经远超过材料的耐温极限，为了保证燃气轮机安全、高效和长期地运行，就必须采用合理的冷却方案。交叉肋通道是一种特殊的内部强化扰流肋结构，最早由前苏联设计并使用，且取得了较好的效果，近年来越来越多的研究人员开始研究这种特殊的冷却结构[1]。

国外方面，Nagoga[2]将前苏联和俄罗斯的涡轮叶片中的交叉肋通道进行了系统性的总结，发现交叉肋通道不仅具有高于普通蛇形通道以及柱肋通道的换热能力，还具有适应陶瓷材料熔模铸造技术的高鲁棒性和较高的叶片强度，可以使高压涡轮叶片尾缘处的寿命提高约40倍。Bunker[3]采用实验的方法对平板交叉肋通道的流动换热情况进行了研究，通过液晶和红外热像方法对不同几何结构的交叉肋通道测量后发现，当雷诺数在2×104到1×105之间时，交叉肋通道的换热能力是光滑通道的2.5～3倍。Ramireddy等[4]采用数值模拟的方法在两层交叉肋通道的基础上研究了矩形截面和U型截面三层交叉肋通道，结果发现三层交叉肋通道的综合换热效果要低于两层交叉肋通道，原因是阻力大幅度增加。

国内方面，张勃等[5]对不同几何参数的交叉肋通道进行了实验研究，结果发现当雷诺数在5×104到1.2×105之间时，交叉肋通道的换热效果比光滑通道提高了5～9倍，而总压损失增加了3个数量级。李俊山[8]和苏生等[9]分别对高温涡轮的导叶和动叶交叉肋通道进行了耦合数值研究，对导叶的计算结果发现当冷气流量为1.245%时叶片平均温降为350 K，而且温度均匀性好，这既节省了冷气消耗量又提高了叶片寿命。对动叶的研究结果表明子通道的宽度与高度比减小会增加流动阻力，子通道较多、肋间距较小的交叉肋通道有利于冷却工质流量分配均匀以及温度分布均匀。

为了尽可能提高交叉肋通道性能，本文通过改变肋倾角、肋宽/子通道宽以及子通道数，获得了多种不同结构的交叉肋通道。利用商业软件CFX对其进行数值计算，详细研究其流动换热性能。

1 数值计算模型与方法

1.1 数值计算模型

为了更真实地模拟交叉肋在真实叶片中的流动换热情况，本文参考某涡轮叶片内部的结构尺寸给定整个冷却通道的大小。冷却通道长67.18 mm，宽35.36 mm，高5 mm，水力直径D为8.76 mm，进出口段分别延长45 mm用来消除流动不充分的影响。在冷却通道中放置不同几何参数的交叉肋形成不同的交叉肋冷却通道，为了研究不同肋倾角、肋宽/子通道宽和子通道数的流动换热影响，本文建立了7种几何模型，表1为各个模型的几何参数。图1为方案2模型图。

表1 模型参数

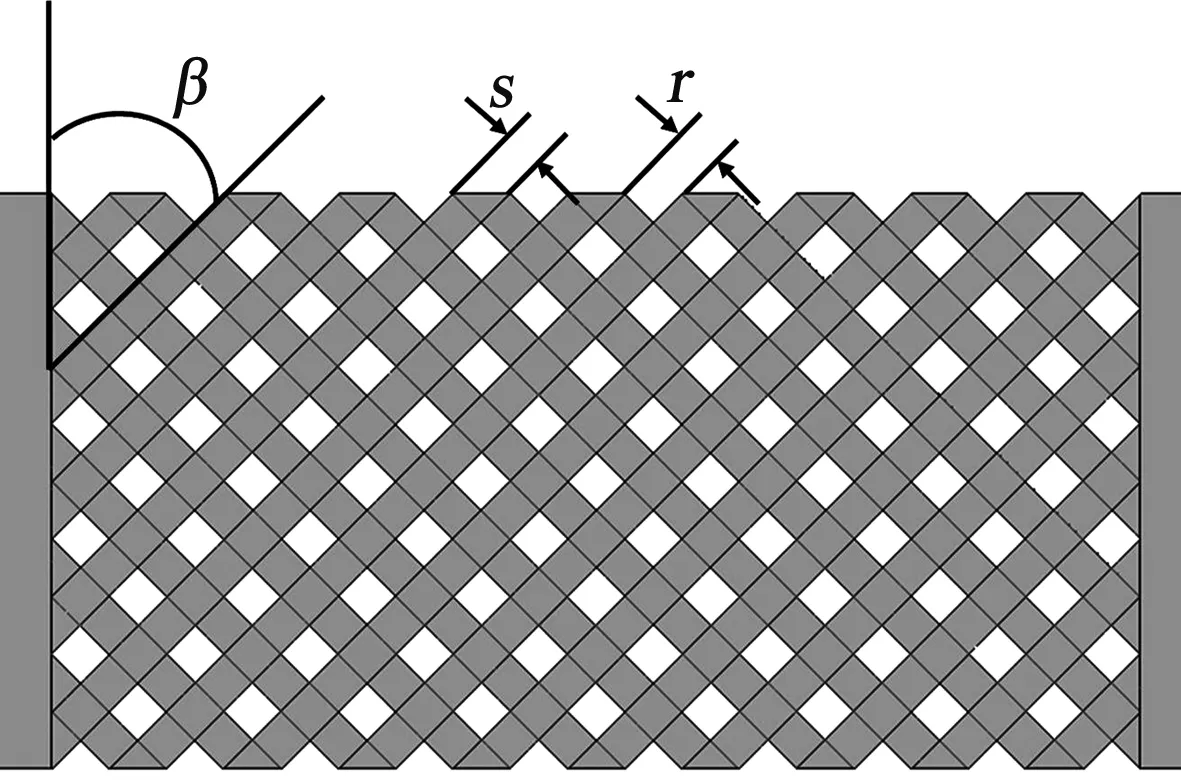
图1 数值模拟计算域模型

1.2 数值计算边界条件

本文使用商业软件CFX进行求解计算，湍流模型选择SST湍流模型，计算工质选择理想气体，进口根据不同的雷诺数给定不同的质量流量，进口气流总温设置为298 K，湍流度为5%，出口边界设置平均静压为大气压1 atm，进出口的光滑延长段壁面设为绝热段，所有交叉肋壁面为等温边界条件，设置温度为340 K。计算精度为高阶精度，残差设置为1×10-6。

1.3 数值计算网格

本文采用ICEM CFD软件进行网格划分，对交叉肋通道划分六面体结构化网格，经无关性验证后网格数量为800万左右，对子通道入口以及折转角的三角形区域采用Y型剖分，对所有壁面处的网格进行加密处理，第一层网格高度为0.002 mm，膨胀比为1.2，子通道网格节点数量根据不同的几何模型单独确定。

图2 计算网格

1.4 数据处理

在涉及流动传热问题时，一般都对物理量采取无量纲化处理，下面对本文中涉及到的部分无量纲处理进行说明。

整个通道的阻力系数f定义为

(1)

式中 ΔP——进口和出口的总压差/Pa;

ρ——进口冷气的密度/kg·m-3;

U——进口平均流速/m·s-1;

D——水力直径/m;

L——传热区的流向长度/m。

使用f/f0来衡量阻力增大的程度，对于相同水力直径光滑通道阻力系数f0的计算，本文采用Karman-Nikuradse公式

f0=2×(2.236lnRe-4.639)-2

(2)

努赛尔数的计算公式为

(3)

式中h——对流换热系数/W·(m2·K)-1;

λ——流体的导热系数/W·(m·K)-1，对于光滑通道充分发展的努赛尔数Nu0的计算选择著名的Dittus-Boelter关联式

Nu0=0.023·Re0.8·Pr0.4

(4)

式中Re——进口雷诺数;

Pr——普朗特数，Dittus-Boelter关联式适用于流体与壁面为中等温差的情况，一般对于气体工质不超过50 K。

为了综合考虑换热能力和阻力损失的情况，引入综合热效率TPF，定义为

(5)

2 计算结果分析

由于交叉肋整体结构以及流动机理相似且上下对称，本文选取方案2的单层通道进行分析，图3(a)为其整体的速度流线图，每个子通道流线用不同的颜色表示以便更好地观察其流动情况。从图中可以发现，在子通道进口处，由于肋倾角的存在，流体直接冲击右侧壁面，导致通道两侧的流动差异。流体在流经第一个折转角前的流动相对平滑，基本沿着子通道流动，流向另一层的流体很少。但是在入口处的第一个交叉口，流体直接冲击壁面，迫使一部分流体从第一个交叉口流向另一层子通道，随后沿着另一层子通道流动，在另一层子通道折转角前的交叉口处又流入原层子通道。从图3(b)的局部流线图可以看到，流体在折转角前会形成二次回流产生阻塞作用，同时还会在三角形交叉口处生成纵向涡，而在折转角之后流体会沿着子通道呈螺旋式向前运动。

图3 流线分布

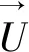
图4 场协同角分布云图

图5为不同肋倾角交叉肋通道在不同进口雷诺数下的努赛尔数变化曲线，方案1的肋倾角为35°，方案2的肋倾角为45°，方案3的肋倾角为55°。可以看出，当进口雷诺数增加时，三种肋倾角结构的换热效果也随之增加。不同肋倾角的换热强弱存在较大的差异，肋倾角35°的换热能力最强，其次是肋倾角45°，肋倾角55°的换热能力最弱。这主要是因为肋倾角越小，整个交叉肋通道的折转角越多，而在折转角处的流动对壁面具有很强的冲击和扰动作用，增强了换热。此外，由于肋倾角的减小，在进口处来流的流体对肋侧壁面的冲击作用会增大，这也能增强换热能力。

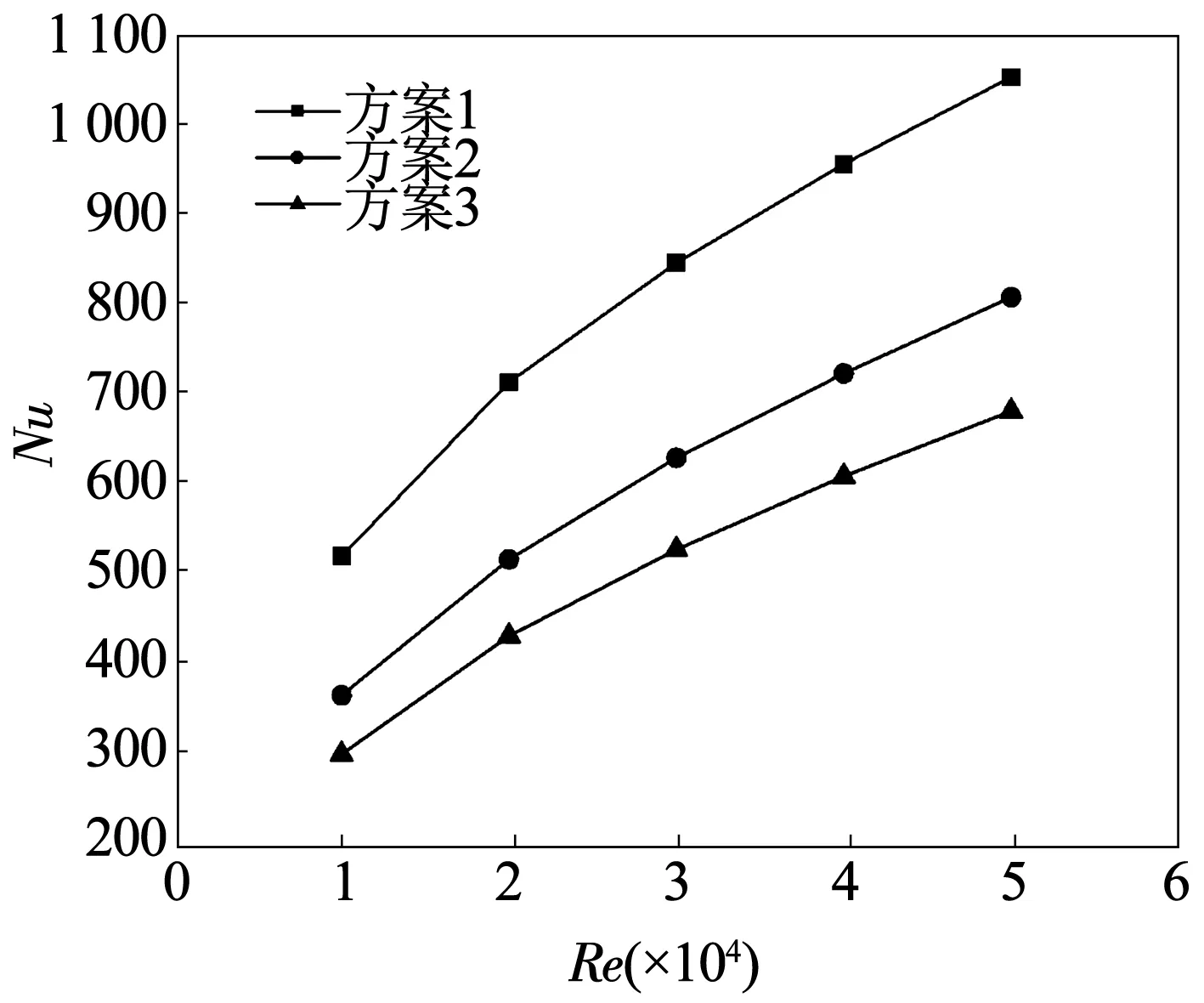
图5 不同肋倾角的Nu变化曲线

图6为在雷诺数Re=30 000时，不同肋倾角通道的基本面努赛尔数分布云图，冷却工质从下方流向上方。从云图上不难发现，整体换热能力35°肋倾角最强，55°肋倾角的换热能力最弱。在靠近入口处，35°肋倾角和45°肋倾角侧壁面受到的流体冲击比较强烈，并且流体刚进入通道还未被加热，温度相对较低，因此在靠近入口处出现了强换热区。由于肋片的斜置偏转，通道右侧的换热能力要比左侧高一些。三种角度的通道在折转角处均出现强换热区，这主要是因为在折转角处，气流冲击壁面，并且上下翻转，使流体掺混剧烈，由上文的的分析可知还会产生能够增强换热的纵向涡，并且肋倾角越小，作用越剧烈。

图6 不同肋倾角的Nu分布云图

图7为进口雷诺数Re=30 000时一半肋高截面速度大小分布云图，用进口平均速度Uin做归一化处理。从图中可以看出，不同肋倾角通道的速度大小分布差异较大，肋倾角越大，速度分布越均匀。55°肋倾角通道相对另外速度分布更加均匀，速度基本在Uin的3～6倍左右，特别是在折转角附近速度更小，接近进口速度。对于35°肋倾角，速度的不均匀性显著增大，特别是在下游靠近出口的区域，通道中的流速达到了Uin的12倍以上。同时在肋折转角附近也存在低速区，速度大小和进口速度接近，流动阻塞十分明显。

图7 不同肋倾角的U/Uin分布云图

图8为不同肋倾角通道的f/f0随雷诺数的变化曲线。从图8可以看出，交叉肋通道的阻力系数为光滑通道的250～2 500倍左右，并且随着雷诺数的增大，阻力系数比呈现上升趋势。随着肋倾角的减小，阻力系数急剧增大，因为肋倾角的减小不但增加了折转角的数量，还增加了流体与壁面的接触面积，从而使摩擦损失增大，进而使阻力损失增加。

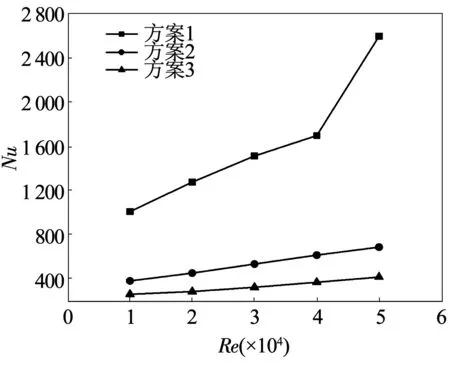
图8 不同肋倾角的f/f0变化曲线

图9为综合热效率TPF随雷诺数的变化曲线，从图中可以看出，不同肋角度的TPF都随着雷诺数的增大呈现降低的趋势。当Re=10 000时35°肋倾角通道的TPF最大，而在其他雷诺数范围内，45°肋倾角的TPF要高于另外两个通道。

图9 不同肋倾角的TPF变化曲线

图10为不同的肋宽/子通道宽的交叉肋通道的努赛尔数随雷诺数变化曲线，所有的方案肋倾角都为45°，子通道数为10个，方案2肋宽/子通道宽为1，方案4为0.5，方案5为1.5。从图中可以看出，方案5的换热能力最强，方案2次之，方案4最弱，说明随着肋宽/子通道宽的增大，冷却通道的换热效果越好。因为在保持其他条件不变时，增大肋宽/子通道宽，相当于减少了通道的通流面积，因此在相同的质量流量下，流体的流速必然增大，这一方面会使流体对壁面的冲击和扰动更大，另一方面流体加速对附面层的破坏更大，带来的掺混作用也更强，并且产生强烈的二次流，从而增强了换热能力。

图10 不同肋宽/子通道宽的Nu变化曲线

图11为在雷诺数Re=30 000时，不同肋宽/子通道宽的交叉肋通道的基本面努赛尔数分布云图，流向自下而上。不难发现，强换热区出现在进口以及折转角处，因为进口处存在肋倾角，流体进入子通道冲击壁面，而到了折转角处又对壁面产生冲击和扰动，流体上下翻转。换热能力随着肋宽/子通道宽的增大而增大，这主要是流速的变大导致的冲击、扰动和掺混等作用的加剧，而且在上下通道连通的交叉位置，两个子通道的流体速度之间存在一个夹角，当流速增加，上下之间的气体之间的掺混作用进一步加剧，因此当肋宽/子通道宽增大时，换热能力显著增强。

图11 不同肋宽/子通道宽的Nu分布云图

图12为一半肋高截面处当雷诺数Re=30 000时速度大小分布云图，同样速度用进口平均速度Uin做归一化处理。可以看到，当肋宽/子通道宽为0.5时，速度的变化相对较小，即使在流经出口处的加速段，流速才达到Uin的5～6倍左右。而当肋宽/子通道宽为1.5时，在子通道进口处速度就能达到6倍的Uin以上，中间区域的速度为Uin的8～10倍，而在出口处流速则达到了Uin的12倍以上。造成这种差异的主要原因有两个，其一，子通道变窄导致了通流面积减小，从而在进口条件相同时流速变大；其二是当流速变大，换热能力就会增强，流体的温度随之提高，引起密度减小，从而使流速又一次变大。同时在各个模型的折转角处都存在低速流动区，速度大小接近进口速度，即使子通道变宽，通道面积增加，也仍然存在不会被消除。

图13为不同肋宽/子通道宽的f/f0随雷诺数的变化曲线，从图13可以发现，随着雷诺数增大，阻力系数都增大，与光滑通道相比，交叉肋通道的阻力损失显著增加。方案5的阻力系数要大于方案2，方案2的阻力要大于方案4，这说明在其他条件相同时，子通道越窄，其阻力损失越大。因为在子通道变窄后，流体流速增加使得流体和流体以及壁面之间的作用更加复杂，冲击、扰动和掺混作用更剧烈，而且在产生二次流之后，窄通道的阻塞效果更加显著，导致阻力损失增大。

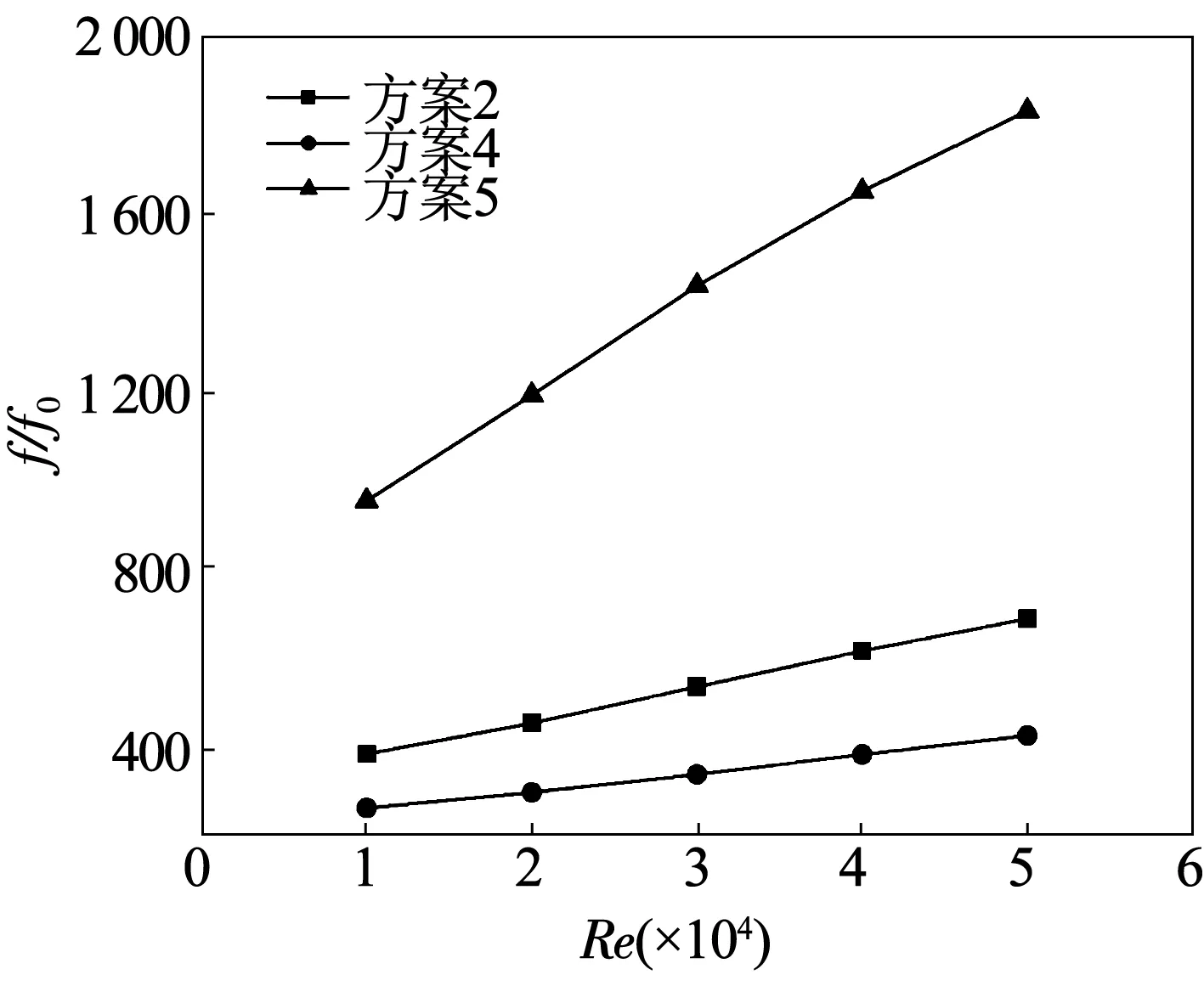
图13 不同肋宽/子通道宽的f/f0变化曲线

图14为不同肋宽/子通道宽的f/f0和TPF随雷诺数的变化曲线，在不同的雷诺数下，方案2的综合热效率TPF都要高于其他两个方案，方案5的TPF都最低，这说明肋宽/子通道宽既不能太小也不能太大，太小换热能力相对较小，导致TPF偏低，而太大则会导致阻力损失急剧增加，导致TPF较小，因此在设计交叉肋结构时，不能一味只追求换热能力而增大肋宽/子通道的值，还应该考虑其带来的过大的阻力损失。根据计算的结果我们可以推断：在给定其他条件下，存在一个最佳的肋宽/子通道宽，使得综合热效率TPF最高。

图14 不同肋宽/子通道宽的TPF变化曲线

图15为不同子通道数条件下的努赛尔数随雷诺数变化曲线，所有方案的肋倾角为45°，肋宽/子通道宽为1，方案2的子通道数目为10个，方案6为6个，方案7为14个。不难发现方案7的换热能力强于方案2，方案2强于方案6。说明子通道的数目越多，越有利于换热。究其原因主要有两点，一是子通道数的增多会导致子通道变窄，使流体更容易与壁面发生冲击和扰动作用，二是子通道数目的增加会增加折转角的数量以及上下层通道的交叉口数量，而这些区域的流体作用均非常剧烈，在折转角处的冲击翻转和交叉口处的上下层对流掺混等作用均极大的强化了换热，所以通道数越多换热能力越强。

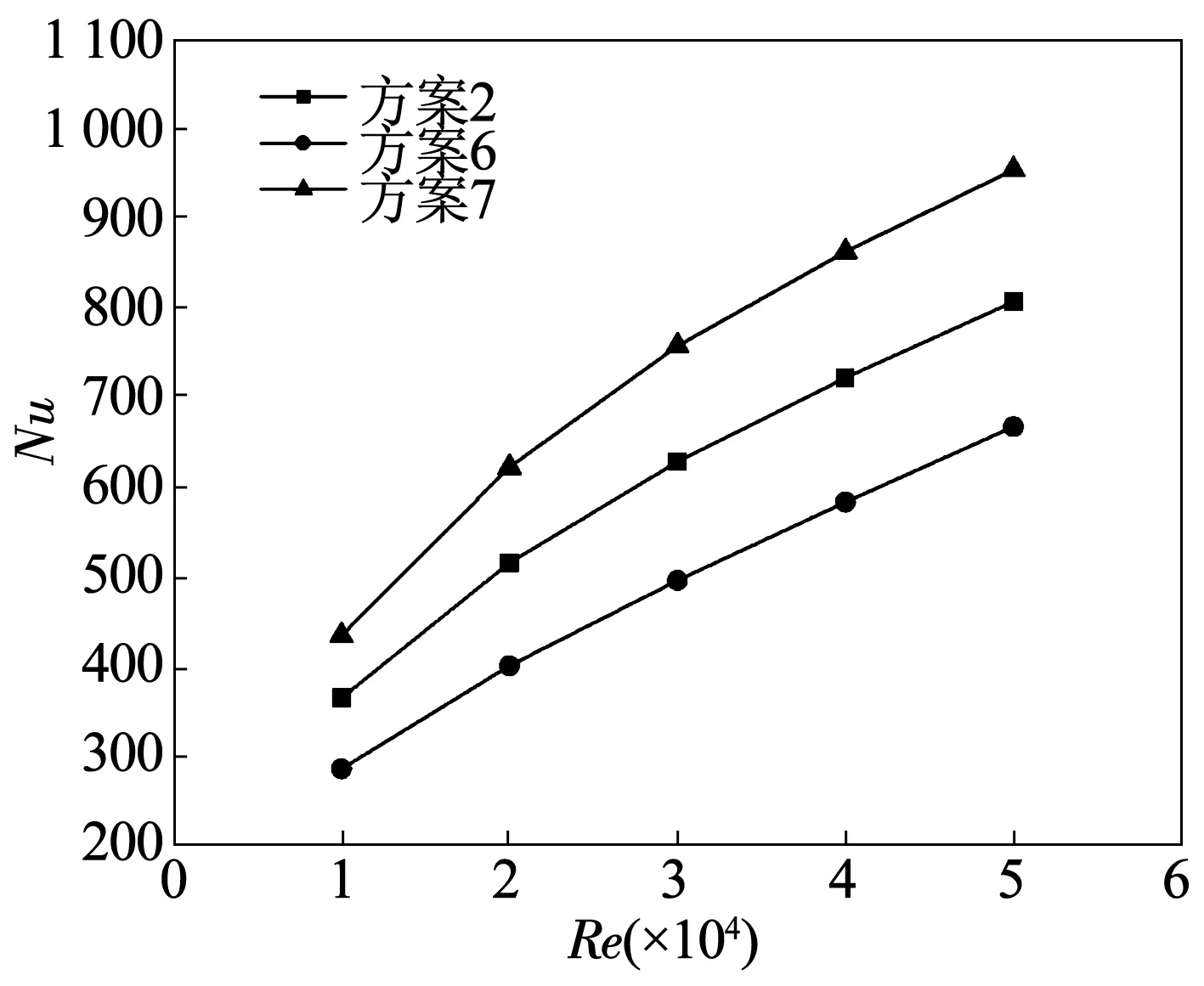
图15 不同子通道数的Nu变化曲线

图16为在雷诺数Re=30 000时，不同子通道数目的交叉肋通道的基本面努赛尔数分布云图，流体流动方向从下到上。从图中可以看到，子通道数越小，换热分布越均匀，主要是因为通道的折转角数量和上下层交叉口的数量减少，流体与流体及壁面的作用效果变弱。整体来看，随着子通道的数目增加，虽然增强了进口处的换热能力，但是同时也稍微削弱了出口处的换热，因为增加了流体的流经的沿程长度，并且子通道的侧壁面数量显著增加从而增加了流体与侧壁面的冲击和扰动，导致流体的温度在通道前半程就已经大幅度升高，到了出口处与壁温相差很小，从而换热效果减弱。与其他结构的交叉肋通道类似，流体在入口处和折转角处的冲击以及翻转等作用使这个两个区域为强换热区。

图16 不同子通道数的Nu分布云图

图17为进口雷诺数Re=30 000时一半肋高处截面的速度大小分布云图，用进口平均速度Uin做归一化处理。不难发现，三种方案的大多数区域速度大小都在Uin的4～7倍之间，当子通道数目为6个时，由于子通道宽度增大，流程变短，速度分布比较均匀，折转角处的二次流和阻塞效果减弱，因此折转角附近的低速区较小。子通道数为10个和14个时，其速度大小分布十分类似，流体在子通道的进口处速度为Uin的3～5倍左右，中间区域为Uin的6倍左右，在出口处的速度能达到8～9倍Uin左右，主要是因为子通道数增多后换热面积以及通道的流向长度都会增加，从而引起了流体的温度升高，密度减小，由于流体的连续性，因此流速会逐渐增加。

图17 不同子通道数的U/Uin分布云图

图18为不同子通道数的f/f0在不同雷诺数下的变化曲线，进口雷诺数越大各个方案的阻力损失也越大，方案7的阻力损失最大，方案6的次之，方案2的最小，不难发现阻力损失并不是通道数越多越大，方案2的小于方案6，究其原因是通道数减小导致了子通道的水力直径增大，从而使子通道的雷诺数增大，进而导致了阻力损失增大，对比方案2和方案6，子通道雷诺数对阻力损失的影响要大于子通道数增加而导致的折转角以及侧壁面等增加的影响。而方案7的阻力损失最大，说明子通道数增加而导致的阻力损失的增加量超过了子通道雷诺数增加导致的阻力损失的增加量。

图18 不同子通道数的f/f0变化曲线

从图19的综合热效率TPF分布曲线可以知道，方案2和方案7的TPF大小相差较小，方案7要略高于方案2，而方案6的TPF要远低于另外两个方案，因此在选择交叉肋的子通道数时，不应过小，这既会导致换热能力减弱，还会一定程度上增加阻力损失，导致TPF偏低，应该综合考虑选择合适的子通道数。

图19 不同子通道数的TPF变化曲线

3 结论

本文利用数值模拟的方法对在一定雷诺数范围内不同几何参数的交叉肋通道的流动和换热特性进行了研究。得到了以下的结论：

(1)交叉肋通道对冷却气体的流动和换热能够产生巨大的影响，使流体产生二次流和纵向涡，能够极大程度的强化换热，但同时阻力损失也会急剧增大。在本文的计算模型和工况下，交叉肋通道的换热能力为光滑通道的6～16倍，阻力系数为光滑通道的250～2 600倍。

(2)肋倾角的减小能够增加折转角的数量以及入口处流体对壁面的冲击作用，从而增强换热能力，同时增大阻力损失。

(3)肋宽/子通道宽的增大，会使子通道的通流面积变小，增大流体的流速，产生更大的冲击、扰动和掺混作用，从而增强换热能力，增大阻力损失。

(4)子通道数目的增加会使的子通道变窄，同时还会增加折转角以及上下层交叉口的数量，使流体更容易与壁面发生冲击和扰动作用，从而增强换热能力，但对于阻力损失，没有明显的规律。