结合源-网-荷信息的风电爬坡事件综合识别方法

汪岩佳，赵志刚，万 杰,3，任国瑞，王 玮，于继来,3

(1.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150000；2.吉林龙源风力发电有限公司，吉林 长春 131500；3.哈尔滨工业大学电气工程博士后流动站，黑龙江 哈尔滨 150000；4.新能源电力系统国家重点实验室(华北电力大学)，北京 102206)

0 引言

当前，我国的可再生能源发展十分迅猛，国家能源局统计数字显示：2018年风电装机和光伏发电装机同比增长12.4%和34%。然而，在全国风电实现弃电量和弃风率“双降”的同时，新疆、甘肃、内蒙古三地的弃风率却仍然高达23%、19%、10%。造成上述弃风问题的主要原因之一就是：风电具有强不确定性。其中，长时间极端气象引发的功率爬坡事件是风电不确定性的一个重要表现[1-2]。大规模风电爬坡会对电网的安全稳定、调度规划和实时控制造成重大影响和危害[3-4]，如2008年发生在美国德克萨斯风电场的功率爬坡事件。因此，其长期以来都是风电领域的研究重点之一，美国ANL国家实验室还专门对风电爬坡事件撰写了一份研究报告，最新的爬坡事件预测研究探讨了半监督学习方法的应用[5]。因此，需要利用合理的风电爬坡事件的综合定义与识别方法，为电网有效控制提供丰富的决策参考信息[6-7]。

目前，针对风电爬坡事件定义与识别的研究较多且较为深入。一般，定义方法可概括为4 种，重点考虑3个关键因素：爬坡方向、持续时间及爬坡的幅度[8]。文献[8]指出：现有4 种定义方法的关键和相同之处是风电功率变化时间间隔和阈值的选取，影响到爬坡事件的有效识别。然而，爬坡定义和标准受实际多种因素约束难以将其统一。针对功率爬坡事件预测，文献[9] 提出了一种具有分布鲁棒性保证的爬坡事件概率估计的不确定性量化模型；文献[10]提出了一种基于典型事件聚类的识别策略。但是，传统的爬坡事件识别方法大多只考虑了源侧的风电场输出功率信息，综合考虑电网侧和负荷侧信息的研究相对较少[8]。文献[11]指出可再生能源与负荷出现相反方向的爬坡事件会对电网产生更严重的影响，未来的爬坡事件研究，不仅需要在预报时引入数值预报信息[12]，还需要在定义与识别时引入负荷侧等更多信息。因此，如何全面的结合源侧、网侧及负荷侧的更多信息对风电爬坡进行综合定义和识别，是一个需要继续研究的问题。

本文在利用源侧风电场输出功率曲线与对应的电网负荷侧曲线获取的相对风电功率曲线上定义爬坡事件，并根据电网频率变化的允许值设定用以识别爬坡事件的判断阈值；最后，通过对风电功率曲线的定义进行了初步延伸，从而提出了一种结合广义源-网-荷信息的风电爬坡事件综合识别方法。

1 爬坡事件的相对风电功率定义策略

1.1 相对风电功率的定义策略

对电网的可靠运行、调度规划和实时控制三方面会造成重大影响和危害的风电功率变化，是风电爬坡事件进行定义时需要考虑的关键因素。然而，当风电变化趋势与电网负荷需求一致的时候，即便较大的风电场输出功率变化对电网也是有利；当风电场输出功率变化趋势与电网负荷需求相反的时候，即便是较小的风电场输出功率对电网也是有害的。因此，若在风电场/群的输出功率(以下都简称为“风电功率”)陡增时，负荷曲线也出现同样的陡增现象。这时，虽然风电场功率增大，但是负荷需求量也增加，电网的有功功率仍然保持平衡；因此，这种风电爬坡是不会对电网产生影响。但仅从风电场功率来描述，风电的这种大功率变化情况是会被定义为爬坡事件的。所以，在描述爬坡事件时，应根据风电的正反调峰特性同时考虑场-网两侧的功率曲线变化情况，与文献[8]所提出的研究展望是一致的。因此，本文利用相对风电功率曲线来定义爬坡事件。

设风电场输出功率曲线的时间序列为P(t)，区域总负荷曲线为Q(t),风力发电所对应的部分负荷功率曲线的时间序列为q(t)，定义相对风电功率曲线的时间序列为P′(t)，则

P′(t)=P(t)-q(t)

(1)

式中，q(t)=n%Q(t)，n%为风电场额定输出功率在区域电网所有发电中的占比。

1.2 利用相对风电功率对爬坡事件进行定义

爬坡定义的一个重要表征量是风场输出功率的变化值(即幅度变化)，其表示在一个时间段内的风电功率变化情况。若某段时间出现风电爬坡事件，相对风电功率陡升或陡降，首末两时刻的功率差值较大；不发生爬坡事件时，相对风电功率曲线平稳，首末两时刻的功率差值较小。因此，本文用t到t+Δt时间段的首末时刻的相对风电功率值的变化量来定义爬坡事件

|P′(t+Δt)-P′(t)|>Pval

(2)

式中P′(t)与P′(t+Δt)——t和t+Δt的相对风电功率值;

Pval——相对风电爬坡阈值；

风电爬坡时，相对风电功率P′(t)与P′(t+Δt)的差值会变大(陡变)；当差值大于阈值Pval时，认为发生了爬坡事件。而当相对风电功率稳定，不发生爬坡事件时，P′(t)与P′(t+Δt)的差值小于阈值Pval。

1.3 基于实际数据的爬坡定义合理性分析

如图1所示，为风电场某一时段1内的输出总功率及其对应负荷情况。此时，风电场输出功率陡升，而负荷侧功率平稳，则电网中的有功功率不再平衡，需要其它形式的发电来参与调节。因此，仅从风电场侧输出功率信息，将该情况判定为爬坡事件是合理的。

图1 时段1的风电场输出功率及对应负荷情况

如图2所示，风电场某一时段2的输出功率及对应电网负荷情况。此时，电网负荷曲线有较大变化，与风电场输出功率的变化趋势一致，如果两者在一定时段内刚好大小相同或者相差无几、可以满足电网功率平衡需求，则此时的爬坡事件不会对电网稳定运行产生影响。所以，此种情况发生时，风电场输出功率虽然有大的波动，但也不算做对电网有影响的爬坡事件。在这种情况下，除非风电场功率的大幅变化已经超过了一定范围，否则仅从风电场侧描述爬坡事件是不合理的，而利用相对风电功率曲线来判定风电爬坡事件更加合理。

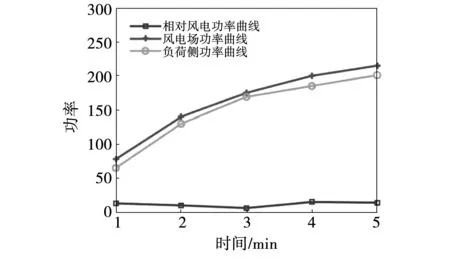
图2 时段2的风电场输出功率及对应负荷情况

图3为风电场某一时段3内的输出功率及对应负荷情况。此时，风电场输出功率较为平稳，但是负荷侧功率曲线出现明显的陡升；虽然，电网有功功率出现不平衡，会对电网的稳定运行产生影响；但是，由于这种影响并不是由风电场输出功率变化引起的，所以在本文中被判定为非爬坡事件。因此，在这种情况下，需要结合风电场输出功率曲线，辅助相对风电功率曲线来做出最终的判定。

图3 时段3的风电场输出功率及对应负荷情况

如图4所示，为风电场某一时段4内的输出功率及对应负荷情况。虽然风电场输出功率发生的变化不大，但由于此时的负荷侧功率曲线也出现一定变化；单独一个变化，可能不足以导致电网功率出现较大波动，但两者同时出现则可能引起较大网侧扰动。因此，该情况下使用相对风电功率曲线来判定爬坡事件更合理一些。

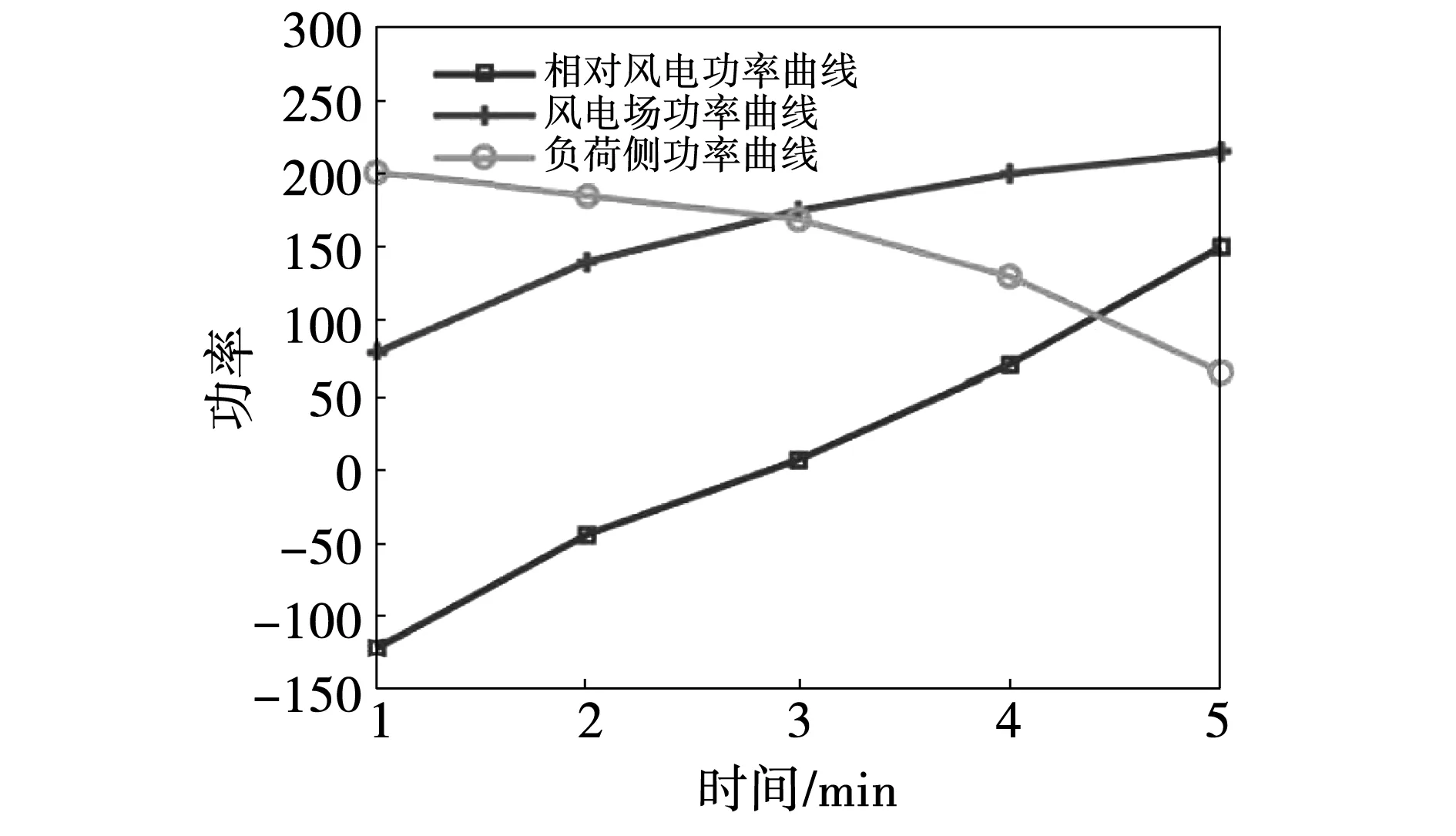
图4 时段4的风电场输出功率及对应负荷情况

根据上述分析四种情景的分析可知：在相对风电功率曲线上定义和识别爬坡事件要更加合理。

2 利用电网频率的阈值量化选取方法

2.1 基于网频的阈值量化选取方法

对阈值定义方法有很多种，目前研究中使用较多的都是直接选取总装机容量的百分比来设置阈值，但是这种阈值设定方法没有明确的定义，都是直接根据经验值得出。在爬坡事件发生时，有功功率的不平衡一定会对电网的频率产生相应的影响，由此本文根据电网频率变化的允许值，提出了一种能够适用于各类风电场的一种阈值定义方法。

在电力系统中，频率与功率之间的变化主要与电力系统的一次调频和二次调频有关，但二次调频与一次调频相比，对于频率的影响较小，基本可以忽略，因此本文仅考虑电力系统的一次调频，在一次调频的过程中电力系统的有功功率的变化量与频率的变化量之间的关系为

kσ=-Δf(%)/ΔP(%)

(3)

式中 Δf(%)——电网频率变化的百分数；

ΔP(%)——调频机组有功功率变化百分数；

kσ——调差系数。

进一步，可得到

ΔP(%)=-Δf(%)/kσ

(4)

设P额为电网总装机容量，风电场占总装机容量的n%，根据国家供电营业规则规定，电网总装机容量在300万kW以上的供电频率允许偏差为0.2 Hz；电网总装机容量在300万kW以下的供电频率允许偏差为0.5 Hz；而调差系数kσ一般为4%～6%，我国电网频率要求为50 Hz，则相对风电爬坡阈值可设为

Pval=α×(P额×n%)/(50×4%)

(5)

当选取样本大于300万kWh，α=0.2；当选取样本的装机容量小于300万kWh，α=0.5。

当|P′(t+Δt)-P′(t)|>Pval时，即为相对风电功率出现对电力系统有影响的电力爬坡事件。

2.2 与传统方法的对比分析

为了表明该方法的有效性，利用文献中典型经验值选取阈值方法进行对比验证。本文选取两个风电场的数据进行阈值选取情况分析，设功率瞬时最大值为额定功率，由于选取的两个风电场的容量均大于300万kW，因此α=0.2。根据公式(5)可以得到两个风电场阈值选取情况如表1所示。用得到的阈值对原始数据点进行划分，得出发生爬坡事件的样本量与非爬坡事件的样本量所占比例，结果如图5所示；利用考虑频率的阈值量化选取后，两个风电场中爬坡事件的样本点占总量的16.4%和14.2%，这与文献[13]的结果是相符的。

表1 两个风电场的阈值选取情况

图5 经阈值划分后的爬坡事件占比情况

此外，结合相对风电功率曲线利用该网频阈值来判定爬坡事件的方法，会更多地受系统运行方式的变化而自适应性变化。尽管装机短时间内不会变化，但系统负荷、风电运行渗透水平，是不断变化的。如图1～图4所示，同样的风电功率变化，在某些运行方式下可被判为爬坡；而在其他运行方式下，则有可能被判断成非爬坡事件。是否发生爬坡，要决定于风电、负荷及网频等条件。因此，对于现有爬坡定义方法，本文提出的利用考虑电网频率作为阈值的量化选取策略不仅合理可行，而且可进一步体现不断变化的电网运行方式。

3 结合源-网-荷的爬坡事件识别方法

利用相对风电功率曲线上定义风电爬坡事件方法，通过基于网频的方法量化选取阈值，可以得到结合源-网-荷信息的风电爬坡事件识别方法如公式(6)所示

|P′(t+Δt)-P′(t)|>Pval

(6)

式中Pval——基于网频的方法选取的阈值；

P′(t)——相对风电功率曲线的时间序列。

由于Pval的选取主要考虑了电网的频率，而电网中频率受到电网中全部发电机组与负荷的影响，因此P′(t)如公式(7)所示

P′(t)=P(t)-q(t)

(7)

其中P(t)可以延伸定义为电网中全部新能源电场输出功率曲线的时间序列，而q(t)为区域电网中全部负荷曲线的时间序列。

通过公式(7)，可以将电网中源侧各类型新能源出力与负荷侧功率综合考虑，通过利用网频的阈值量化选取，考虑了电网信息，由此实现了结合源-网-荷信息的风电爬坡事件综合识别方法。该方法从电网整体运行的角度出发，对实际调度运行具有重要意义。

4 结论及展望

本文针对结合源-网-荷信息的风电爬坡事件综合识别方法进行了研究，结论如下：

(1)提出了相对风电功率曲线的定义及获取方法，在相对风电功率曲线上定义风电爬坡事件；通过负荷曲线将网侧和负荷侧信息予以考虑，进而使得爬坡定义考虑了风电的正反调峰特性，并给出了基于实际电网负荷及风电场数据的相应分析；

(2)结合电网频率来确定风电爬坡事件的阈值，并给出了不同电网容量的量化选取方法，利用实际风电场数据论证了其合理性；

(3)提出了结合源-网-荷信息的爬坡事件综合识别方法，并将源侧定义从单一风电侧延伸为电网中全体新能源发电，从电网实际调度运行角度，提高了爬坡事件识别方法的合理性与实用性。

本文对风电场出现大规模功率爬坡事件的预警及控制有重要意义。后期，还将进一步研究风电爬坡事件的时空分布特性、精确预报等更深层次的问题。