基于螺旋理论的管道蠕动并联机构的奇异性研究

朱锦翊，张春燕，卢晨晖

（上海工程技术大学机械与汽车工程学院,上海 201620）

机构奇异位形通常指机构失稳、其运动学及动力学性能发生瞬时突变或传递运动及动力的能力失常时机构的位形［1］。多年来许多学者对机构奇异进行了大量研究，其中典型的研究方法有Gosselin等［2］提出的基于机构输入输出速度的分析法、Kumar［3］提出的基于对偶螺旋的概念法、Ma 等［4］提出的机构特征法和Collins 等［5］提出的代数法。另外，针对不同类型的并联机构，Joshi等［6］讨论了少自由度并联机构的雅可比矩阵，并分析了3-RPS 和3-UPU 机构的奇异位形；Wu等［7］提出了可以避免密集的雅可比矩阵计算和方程求解的方法来得到机构奇异位形。上述的分析方法普遍基于代数理论对机构奇异位形进行分类和定义，或基于机构的一些特殊性质对其奇异位形进行求解。由于代数法自身的复杂性及机构的多样性，有些学者采用空间几何解析方法来快速分析机构奇异位形。如：Merlet［8］在并联机构研究中引入线几何法；Zhang等［9］采用线几何法来分析3-RSR多模式移动并联机构在运动过程中的奇异问题；Alamdar等［10］提出在不求解运动学方程的基础上采用几何解析方法求解5R球形并联机构的奇异位形。

输流或传质管道是工农业生产中重要的物质输送工具，近年来得到大量应用。输送管道在使用过程中会产生管道堵塞、管道泄漏等问题，需要配套的巡检和清理装备［11］。管道机器人正是随着输送管道的大量应用而得以快速推广和应用的。研发性能优良的管道机器人具有工程迫切性［12］。本文提出一种可在管道内进行监测和探伤的管道蠕动并联机构，并研究其在移动过程中的奇异问题。奇异是机构的固有特性，处于奇异位置的机构的运动与力学特性均会改变［13］，因此分析机构尤其是移动机构的奇异性具有重要意义［14］。并且，管道蠕动并联机构在结构及蠕动方式上的特殊性使得其一旦发生奇异就会使管道和机构本身不可避免地受到损伤和破坏，尤其是在弯管中，奇异可能会导致机构堵塞或卡死在管道内。因此，采取措施预防机构在管道内移动时发生奇异是十分必要的。由于管道蠕动并联机构在移动过程中的雅可比矩阵十分复杂且求解效率较低，用代数方法求解并不适合。故本文主要通过螺旋理论结合线几何方法，在Fang 等［15］提出的奇异分类的基础上提出并联机构在移动过程中的奇异分析方法。首先分析机构自身支链间的关系，得到其相应的奇异几何关系，再进一步分析机构在移动时发生奇异的约束情况，从而得出相应的机构奇异位形和奇异轨迹，以期为后续机构轨迹的规划提供参考，为样机制作提供理论依据。

1 管道蠕动并联机构的工作原理

本文提出的可折展的管道蠕动并联机构的结构和结构简图分别如图1 和图2 所示。其中：机器人主体为3-（P）URU（P）并联机构，3 根连杆通过3 个移动副P 连接成自由度为1 的等边三角形，构成并联机构的上下平台。3 条URU 支链分别通过两等边三角形顶点对称相连，形成一个上下结构对称的3-URU 并联机构，其中连接支链与平台的是2 个其轴线相互垂直的U 副。6 个驱动电机分别安装在与上下平台平行的UB，i2、UA，i2轴线上，通过对电机的协调控制，可实现上平台（或下平台）在X、Y向的转动和Z向的移动共3 个自由度的运动，从而实现动平台位姿的变化。调节上下平台内的移动副可改变平台的大小。机构整体为具有5 个自由度的3-（P）URU（P）并联机构。

图1 管道蠕动并联机构的结构Fig.1 Structure of pipeline creeping parallel mechanism

图2 管道蠕动并联机构的结构简图Fig.2 Schematic diagram of pipeline creeping parallel mechanism

机构在管道内工作时，通过上下平台的缩放，使平台顶点交替与管道内壁接触从而实现机构的蠕动。其蠕动过程如图3 所示。其中：坐标系O-XYZ的原点O为下平台的中心点，X向平行于A1A3，Y向指向A2点，Z向由右手定则确定。上下平台通过移动副放大尺寸并与管道内壁接触，利用摩擦力使接触平台成为定平台，则另一平台利用移动副缩小后成为动平台；确定动定平台后，机构的蠕动则依靠支链的运动。驱动定平台一侧的电机使得动平台实现沿X、Y向的转动和沿Z向的移动，因此可以满足机构在管道内蠕动的自由度变化的要求［16］。

图3 管道蠕动并联机构的蠕动过程Fig.3 Creeping process of pipeline creeping parallel mechanism

机构的奇异性会对其蠕动过程造成重要影响，故须分析该机构在蠕动过程中的奇异性问题。机构的奇异主要是由于受到了支链的约束影响且在一次运动周期中动定平台发生了转换，为此须先分析3-（P）URU（P）机构自身支链产生奇异时的几何关系，再分析机构在管道内蠕动时的奇异性。

2 并联机构奇异分析流程

并联机构的奇异可分为支链奇异、约束奇异和驱动奇异［15］。通常在机构工作空间内部发生约束奇异或驱动奇异，且其对机构的运动性能产生较大的影响，而支链奇异一般发生在机构工作空间的边界区域，对其运动性能影响较小［17］。若机构运动情况特殊，则支链奇异造成的影响并不可忽略。

2.1 支链奇异

建立机构支链i的运动螺旋系{$i}，并将其转化为矩阵形式Ai，即：

式中：n为支链i中运动螺旋的个数。

Ai降秩时，支链运动螺旋间线性相关，此时支链间的几何关系导致机构自由度减少，机构发生支链奇异［18］。

2.2 约束奇异

根据螺旋理论得出机构支链i的所有运动螺旋系{$i}，运用互易积运算求出支链i的约束螺旋系{$ri}，则机构所有的约束螺旋系构成机构的约束雅可比矩阵Jr，即：

式中：t为支链i的约束螺旋个数。

Jr降秩时，约束螺旋间线性相关，动平台的约束减少，此时支链间的几何关系导致机构自由度增多，机构发生约束奇异［19］。

2.3 驱动奇异

Jq降秩时，支链间的几何关系导致机构仍存在自由度，机构发生驱动奇异［20］。

由Jr与Jq组合可得机构的完整雅可比矩阵J［9］：

综上可知，并联机构在移动过程中的奇异分析流程如图4所示。

3 3-(P)URU(P)并联机构奇异位形分析

3-（P）URU（P）关联机构动平台的自由度主要由URU支链决定，上下平台的P副只改变平台的大小，对机构的约束没有影响。分析机构奇异位形时先分析3条支链间的几何关系。并联机构在管道内的蠕动是一个连续过程，即使在蠕动刚开始时机构奇异对其运动性能影响较小，但在后续的蠕动中该影响会累加，因此须分析机构的3种奇异位形。

3.1 支链奇异位形分析

3-（P）URU（P）机构的支链螺旋如图5 所示。建立支链坐标系oi-xiyizi，支链轴线交汇点为原点oi，xi向平行于$i2轴线方向，zi向为$i1轴线方向，yi向按右手定则选取。

机构支链运动螺旋系为：

图4 并联机构奇异分析流程Fig.4 Singularity analysis process of parallel mechanism

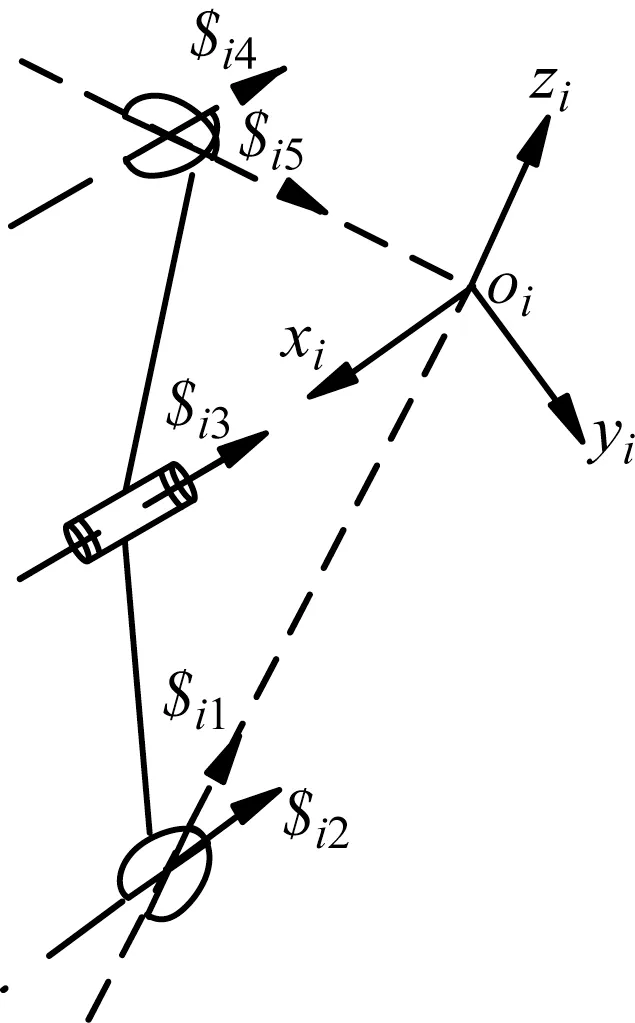
图5 3-(P)URU(P)并联机构支链螺旋示意Fig.5 Schematic diagram of branched chain helix of 3-(P)URU(P)parallel mechanism

式中：b2、b3、b4、c3、c4、m5、n5为不等于0的螺旋参数。

URU 支链轴线上的特殊性导致式（5）中第4 列元素全部为零，所以Ai就简化为5×5 的矩阵M，其秩r(Ai)的变化就可以通过detM来求解。

则：

根据式（7），可知detM=0有2种情况。

情况1：当m5=0时，$i5=( 0 0n5；0 0 0 )，可以看出$i1与$i5线性相关，支链几何关系为$i1与$i5的轴线重合，如图6（a）所示。

图6 3-(P)URU(P)并联机构支链奇异位形Fig.6 Branch chain singularity configuration of 3-(P)URU(P)parallel mechanism

3.2 约束奇异位形分析

以机构定平台为下平台、动平台为上平台为例分析机构约束奇异位形。机构约束力方向为图7中约束螺旋方向，代表支链i所受的约束力，平面S为约束力平面。根据式（2）建立机构的约束雅可比矩阵：

图7 3-(P)URU(P)并联机构各支链约束螺旋Fig.7 Constraint screw of each branch chain of 3-(P)URU(P)parallel mechanism

由螺旋理论可知，3条力线矢只有共轴或共面交汇或共面平行时才线性相关［21］，如图8所示。而机构的$ri1一旦发生线性相关，Jr一定发生降秩，此时机构支链间的几何关系如图9所示。

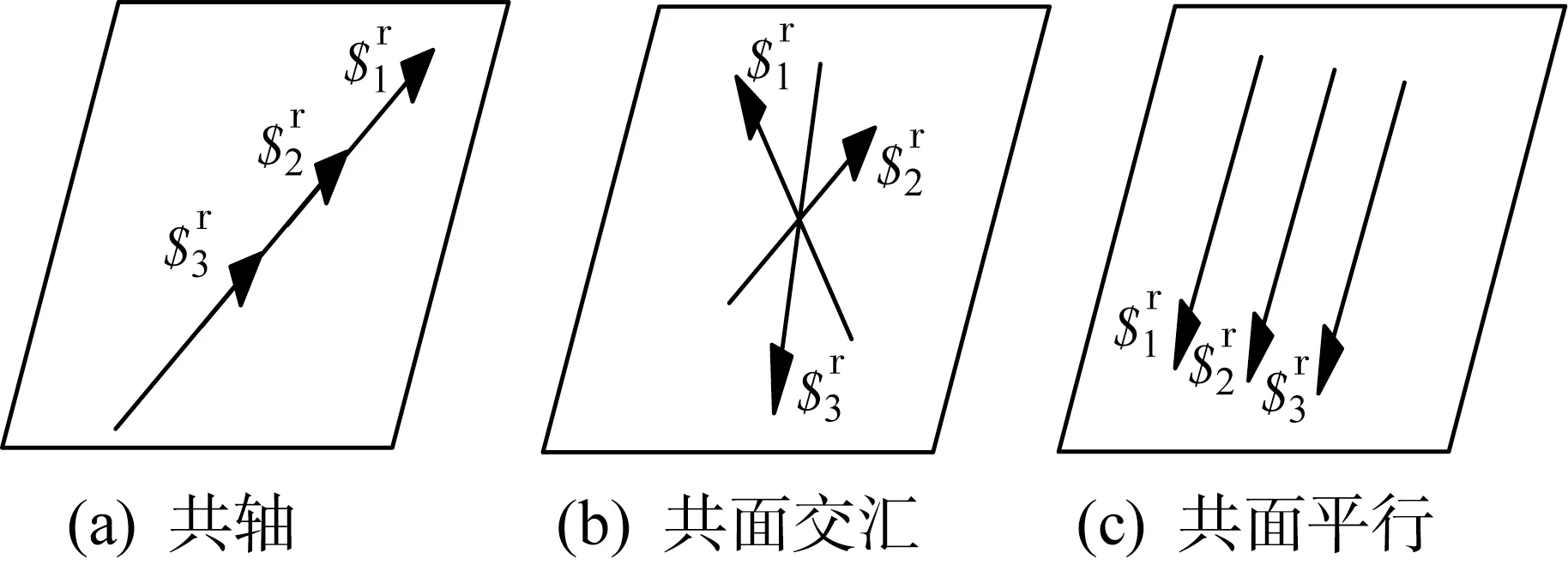
图8 3条力线矢线性相关的几何条件Fig.8 Geometric conditions for linear correlation of three force line vectors

图9 3-(P)URU(P)并联机构约束奇异位形Fig.9 Constraint singular configuration of 3-(P)URU(P) parallel mechanism

3.3 驱动奇异分析

如上所述，钢化支链i的驱动副$i2。钢化后机构支链约束如图10所示。

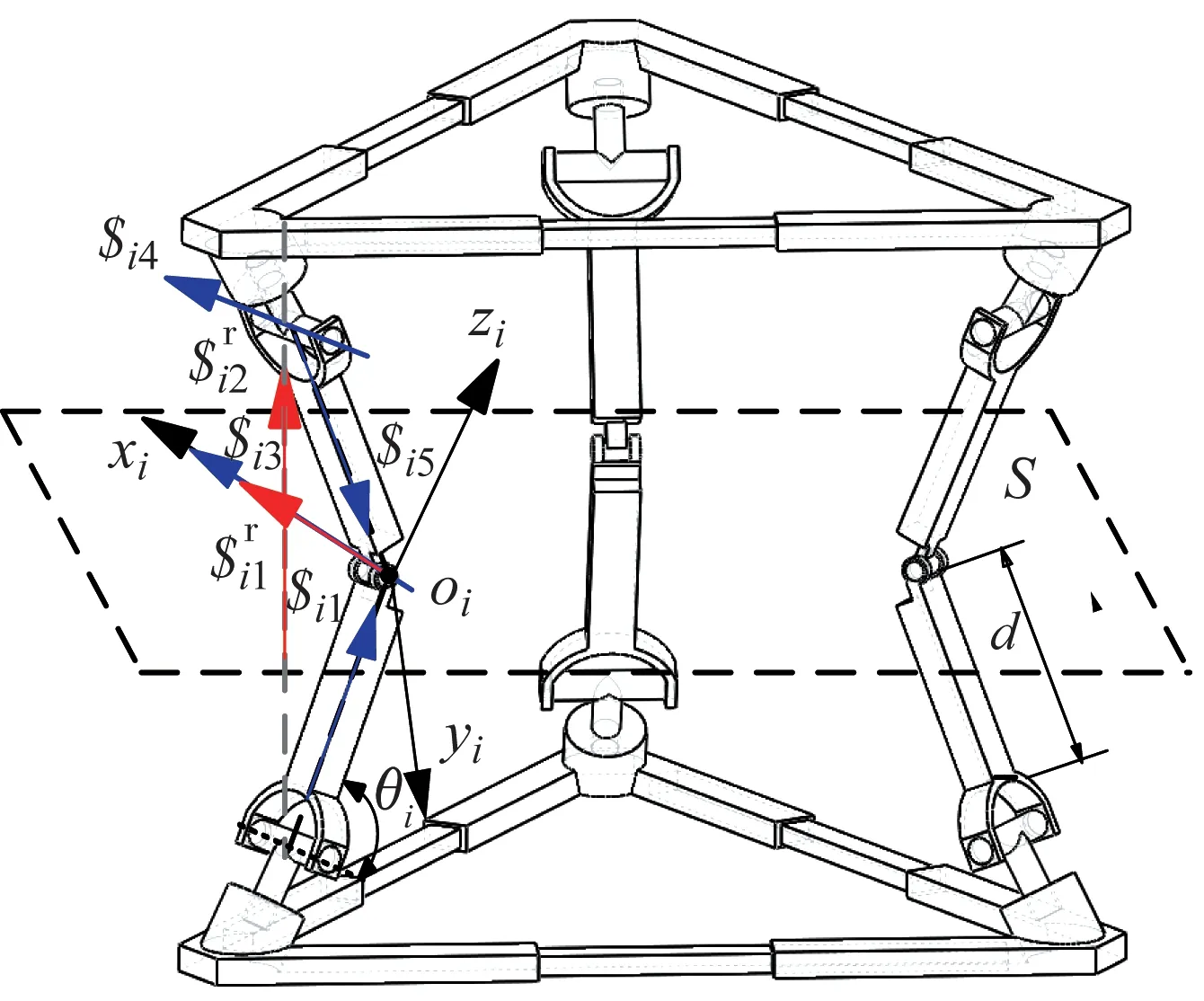
图10 钢化后支链约束Fig.10 Branch chain constraint after toughening

如图10所示，设驱动副的输入角度为θi，连杆长度为d，则支链运动螺旋系为：

约束螺旋系为：

一旦Jq降秩，则会发生驱动奇异。根据式（8），可得机构6×6的完整雅可比矩阵J：

由螺旋的空间几何性质可得机构雅可比矩阵中螺旋空间位置，如图11所示。由此可得Jq中所有约束螺旋的空间位置，如图12所示，表明各螺旋的方向均垂直于约束力平面S，其相互平行。

图11 螺旋的空间位置Fig.11 Spatial position of the screw

图12 约束螺旋$r,2i 的空间位置Fig.12 Space position of constraint screw

由螺旋理论可知［22］，此时最大线性无关组数为3。对机构而言，X、Y方向的转动和Z方向的移动都受到限制。Jq不存在降秩情况，机构支链不存在发生驱动奇异的位置关系。

4 3-(P)URU(P)并联机构在管道蠕动过程中的奇异分析

3-（P）URU（P）并联机构在管道内的一次蠕动通过交替放大、缩小动定平台，用其顶点与管道内壁接触产生的摩擦力将定平台固定，动平台在3条支链的共同驱动下向前运动而得以实现。其中动定平台发生了1次转换，转换后其自身结构没有发生变化，动平台的移动依然由在定平台一侧的电机驱动，机构支链间的奇异性质没有随着平台的转换而发生变化，机构依然等效为3-URU并联机构，驱动副在定平台上。

机构在蠕动过程中的奇异情况会随着管道环境的不同而不同，因此分在直管和弯管内蠕动两种情况分析机构的奇异位形。建立3-（P）URU（P）并联机构的结构示意图，如图13 所示。其中：K为A2A3的中点，B为上平台的中心点；RA，RB分别为AA2、BB2的长度；Ai、Ci的坐标分别为(xAi，yAi，zAi)和(xCi，yCi，zCi)。

图13 3-(P)URU(P)并联机构的结构示意图Fig.13 Schematic diagram of the structure of 3-(P)URU(P)parallel mechanism

4.1 机构在弯管内蠕动

当机构在弯管内蠕动时，协调控制定平台一侧的电机，使得动平台中心点可有效地沿弯管中心轴线移动。在机构蠕动过程中动平台位姿发生变化，而且由于弯管存在X、Y两个方向的空间变化，机构在沿弯管中心轴线移动时只可能发生支链奇异。其奇异位形如图14所示。

由上述分析可得，当机构支链位形如图6（a）所示而Jr降秩时，支链运动的反螺旋系为式（13），其奇异位形如图14（a）所示。

按照图6（a）所示的几何约束，则图13 中A1、C1、B1三点形成一条直线。动平台中心B所能形成的几何约束方程是以B1为球心、半径为RB的球面f(B1，RB)与动平面SB1B2B3相交所得的方程f（B1）。依据d、RB和θ1=60°可得B1的坐标。A1A′1为SB1B2B3的法向量，A1的坐标已知，A1在SB1B2B3上的投影点A′1可通过式（14）求得。在得知A′1坐标后，可求得平面方程f(B1，B2，B3)。

图14 机构在弯管内蠕动时的支链奇异位形Fig.14 Branched chain singular configuration of mechanism creeping in elbow

式中：n为平面SA1B1K的法向量。

由此可得f（B1）的方程式，结合式（16），求解f(B1)即得此时机构奇异位形的奇异轨迹。

当机构支链位形如图6（b）所示而Jr降秩时，支链运动的反螺旋系为式（17），其奇异位形如图14（b）所示。

按照图6（b）所示的几何约束，则图13中A1、B1两点重合，而由于2个U副的间隙导致只能$2与$4重合。动平台中心B所能形成的几何约束方程是以B1为球心、半径为RB的球面f(B1，RB)与平面SA1B1K相交所得的方程f(B2)。已知Ai的坐标且SA1B1K为过A1的中垂面，得平面SA1B1K的方程f(A1，B1，K)。由此可得f(B2)的方程式，结合式（19），求解f(B2)即得此时机构奇异位形的奇异轨迹。

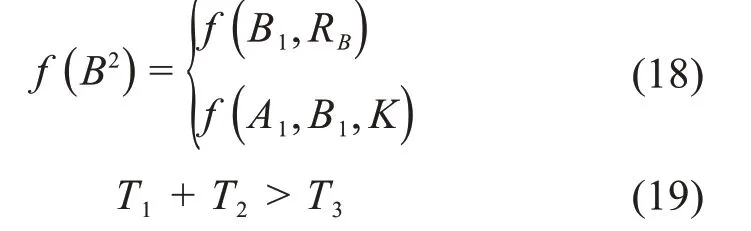
式中：T1、T2、T3分别为RA、RB、d的任意值。

由式（13）和式（17）可知，在该支链奇异下，支链对动平台的约束增加，机构的自由度将减少。机构在弯管内蠕动时，一旦平台处于上述奇异位形，则弯管转向与奇异所增加的约束一致会导致机构处于卡死位置，极大影响机构后续的蠕动。

4.2 机构在直管内蠕动

当机构在直管内蠕动时，同步驱动定平台一侧的电机，使得动平台可以沿直管方向移动。同理，在确定动定平台后机构在蠕动过程中同样存在奇异问题，会影响后续的蠕动。由于机构在直管内运动，其在X，Y方向都将受到约束，因此不会发生支链奇异，只可能发生约束奇异。其约束奇异位形如图15所示。

图15 机构在直管内蠕动时的约束奇异位形Fig.15 Constrained singular configuration of mechanism creeping in straight pipe

按照图9所示的几何约束，则图13中C1、C2、C3三点重合为一点Q。已知|AiBi|=|BiCi|，可得如下约束方程：

d已知，则Ci点坐标就能确定，且Ci点坐标就是Q点坐标，代入式（16）得其几何约束方程f（B3）。结合式（22），求解f(B3)即得此时机构奇异位形的奇异轨迹。根据尺寸条件，可求得输入角度θi=arccos。

4.3 奇异轨迹仿真

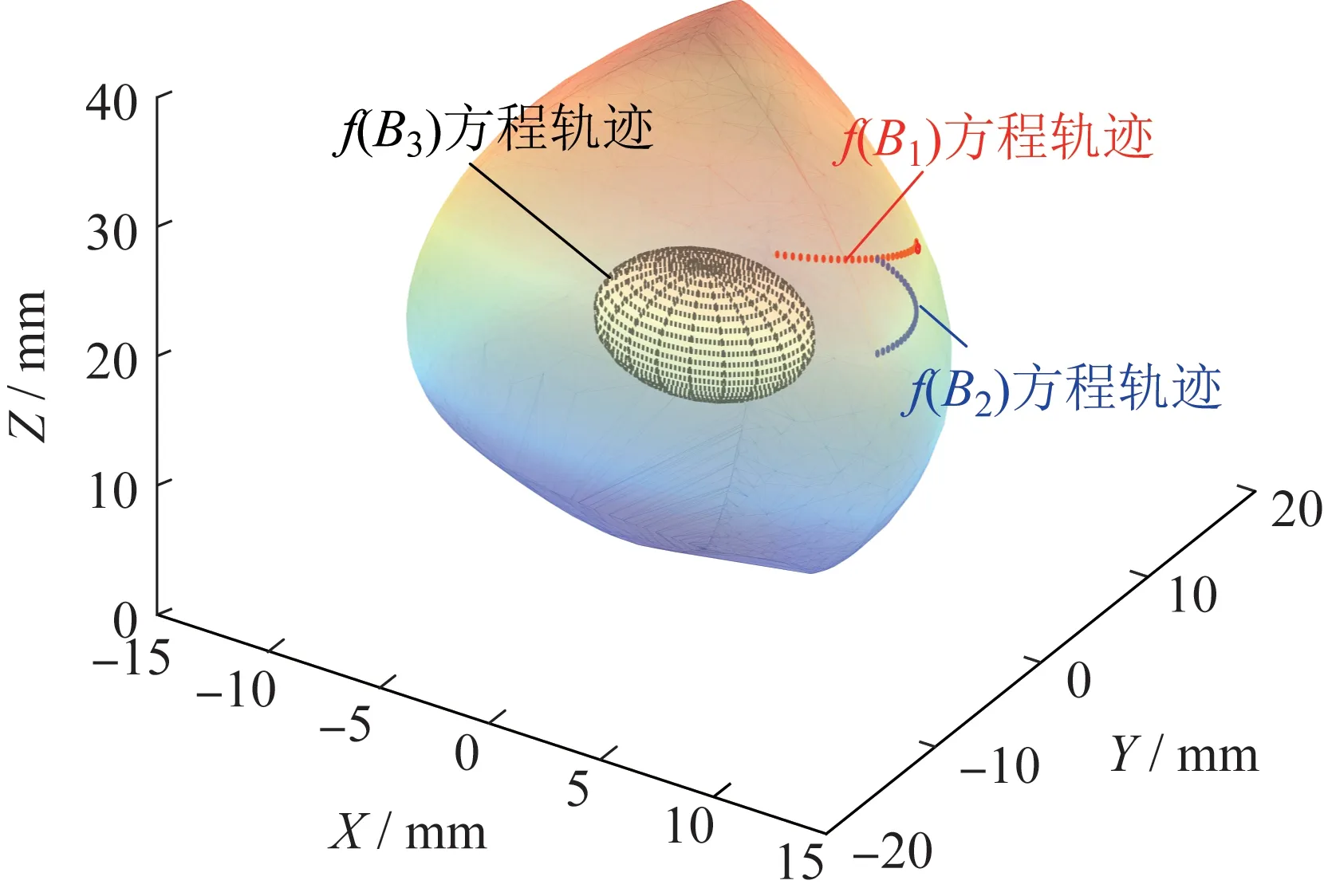
图16 机构在工作空间内的3种奇异轨迹Fig.16 Three kinds of singular trajectories in mechanism workspace

当机构在弯管中发生支链奇异时，尽管由式（15）和式（18）可知奇异轨迹呈圆形，但是受到式（16）和式（19）所示的尺寸约束限制，其轨迹只能为圆的一部分，即为弧线，如图16 中处于工作空间边缘的f（B1）、f（B2）方程轨迹。当机构在直管中发生约束奇异时，图7中原先转化为一个垂直于约束平面的约束力偶和2个约束力［23］会发生变化，此时机构的约束力偶会消失，机构将增加一个沿Z向转动的自由度，并产生绕X、Y、Z三个方向的转动，导致机构动平台中心会形成球面轨迹，即图16 中f（B3）方程轨迹，其处于工作空间的中心位置。

5 结 论

1）依据螺旋理论，提出了一种管道蠕动并联机构的奇异分析方法，并将此方法应用于3-（P）URU（P）并联机构的奇异分析中。分析了机构支链间的约束关系，求解了支链矩阵的行列式，从而得到2种矩阵降秩情况，依此得到了机构支链奇异的2种几何位置关系。

2）根据所提出的方法，建立了机构约束雅可比矩阵Jr，并通过线几何的相关性得到发生约束奇异的一种机构几何位形。建立机构驱动雅可比矩阵Jq，并通过分析得出Jq不会降秩，该机构支链不存在发生驱动奇异的几何位形。依据Jr和Jq建立了该移动机构螺旋形式的完整雅可比矩阵J。

3）在分析了机构支链存在的奇异几何位形后，结合其在管道内的蠕动过程，分析了在蠕动过程中机构的奇异问题。判断出机构在弯管内会发生支链奇异，而在直管内会发生约束奇异，并根据几何约束关系求得奇异约束方程及其轨迹。支链奇异轨迹为位于工作空间边缘的弧线，支链奇异会导致机构自由度减少，如果位置特殊，会导致机构卡死。约束奇异轨迹为位于机构工作中心的球面，会导致机构蠕动的不确定性，也须避免。研究为后续机构在管道中蠕动步态的规划奠定了理论基础。