考虑紧固螺栓的三排滚柱式转盘轴承载荷分布计算
黄龙艺,王 华,嵇 栩
(南京工业大学机械与动力工程学院,江苏 南京 211816)
转盘轴承是大型旋转机械的核心部件,被广泛应用于镗床、塔式起重机、风力发电机、挖掘机和盾构机等设备[1]。按照滚道数量的不同,可将转盘轴承分为单排、双排和三排滚道式等多种类型,其中滚道上的元件为钢球或滚子。与传统小轴承不同的是,转盘轴承具有转速低、尺寸大和承载能力强等特点,其通常承受轴向力、径向力和倾覆力矩的联合作用。因此,可采用静态承载能力作为评估转盘主轴承性能的重要指标。
为了提高转盘轴承的承载能力,确定其滚道上的载荷分布是关键。目前,国内外许多学者针对转盘轴承的载荷分布开展了相关研究。何培瑜等[2]分析了转盘轴承对数修形滚子的力学性能,获得了载荷对滚子边缘应力分布的影响。张占立等[3]通过理论分析和试验验证,探究了四点接触转盘球轴承的间隙和摩擦力矩之间的关系,结果表明轴承间隙与摩擦力矩呈负相关。王燕霜等[4-5]构建了四点接触球轴承的分析模型,并运用Newton-Raphson 法计算了不同间隙下该轴承的载荷分布。赵春江等[6]通过建立角接触球轴承的力学模型,分析了轴承预紧力对滚道接触力的影响。Heras 等[7]建立了一种考虑预紧力、制造误差和滚道变形的四点接触转盘轴承载荷分布计算模型,通过分析获得,在外载荷作用下制造误差对该转盘轴承载荷分布的影响可忽略不计。Gao 等[8]研究了滚道间隙、曲率比和接触角等几何参数对单排四点接触转盘轴承承载能力和使用寿命的影响,通过研究发现,在较大的曲率比和钢球直径下该转盘轴承的力学性能较好。He等[9]建立了三排滚柱式转盘轴承有限元模型,通过将滚道分为淬火层、过渡层和核心层,分析了最大载荷下该轴承滚道上的应力分布,并最终确定了滚道淬火层的最优深度。Peter等[10]采用向量法建立了用于分析三排滚柱式转盘轴承静态承载能力的解析模型,该模型将滚道假设为刚性体,同时考虑了滚道间隙和制造误差对轴承承载能力的影响。Ludwik 等[11]通过建立钢球-滚道的接触模型来分析转盘轴承中钢球与滚道间的接触应力,结果表明,接触角的增大会导致滚道边缘应力集中,从而缩短轴承的疲劳寿命,因此提出了一种滚道边缘修形方法。Aguttebeitia和Daidie等[12-13]分别用壳单元和非线性弹簧单元模拟钢球,以在获取转盘轴承载荷分布时可考虑钢球接触角的变化。王存珠等[14]等建立了单排四点接触转盘轴承的有限元模型,并分析了螺栓预紧力对转盘轴承载荷分布的均匀程度以及最大接触载荷的影响。王永全等[15]基于有限元方法研究了螺栓预紧力与双排点接触转盘轴承载荷分布的关系,发现在非均匀分布的螺栓预紧力下转盘轴承的接触力会出现波动。Wang 和嵇丽丽等[16-17]通过采用非线性弹簧模拟滚子,建立了简化的转盘轴承有限元模型,提高了计算效率,但该模型的有效性须进一步分析。
三排滚柱式转盘轴承的结构复杂,其滚道上的载荷分布容易受到多种因素的影响。螺栓是转盘轴承的重要紧固件,但其对转盘轴承载荷分布的影响无法直接通过理论计算得到。基于此,笔者拟采用非线性弹簧单元模拟实体滚子,通过建立三排滚柱式转盘轴承的有限元模型来分析螺栓预紧力及螺栓结合面处摩擦系数对转盘轴承载荷分布的影响,旨在为转盘轴承的实际工程应用提供参考。
1 三排滚柱式转盘轴承载荷分布计算与验证
1.1 最大载荷计算
以130.20.1005型三排滚柱式转盘轴承为研究对象,其结构参数如表1所示。该转盘轴承紧固螺栓的型号为10.9 级M20 型,其杨氏模量为200 GPa,泊松比为0.3;滚道材料为50Mn,其杨氏模量为208 GPa,泊松比为0.28。
三排滚柱式转盘轴承的结构如图1所示。从三排滚柱式转盘轴承的工作特点出发,可将其承受的载荷分为轴向力Fa、径向力Fr和倾覆力矩M。其中,上排滚子和下排滚子承受轴向力Fa和倾覆力矩M,中间排滚子承受径向力Fr。与轴向力Fa和倾覆力矩M相比,径向力Fr的值往往很小,其对转盘轴承载荷分布的影响不大,在分析中通常可以忽略。为保证计算的有效性,本文将针对有/无中间排滚子的情况,对三排滚柱式转盘轴承上排滚子和下排滚子的载荷分布进行分析。

表1 三排滚柱式转盘轴承的结构参数Table 1 Structural parameters of three-row roller slewing bearing

图1 三排滚柱式转盘轴承结构示意Fig.1 Schematic diagram of three-row roller slewing bearing structure
在轴向力Fa的单独作用下,三排滚柱式转盘轴承内的载荷均匀分布,如图2所示。此时,各排滚子承受的载荷大小相等。在轴向力Fa和倾覆力矩M的联合作用下,方位角不同的滚子承受的载荷大小不同,如图3所示。从理论上分析,三排滚柱式转盘轴承上排滚子承受的最大载荷位于B点,下排滚子承受的最大载荷位于A点。根据美国再生能源实验室推导的经验公式可得[8],三排滚柱式转盘轴承上、下排滚子承受的最大载荷分别为:

式中:Qmax1、Qmax2分别为上、下排滚子承受的最大载荷,N;QMmax为倾覆力矩作用下滚子承受的最大载荷,N;Qn为轴向力作用下滚子承受的载荷,N;N为滚子数量;D为滚道节圆直径,mm。

图2 轴向力作用下三排滚柱式转盘轴承的载荷分布Fig.2 Load distribution of three-row roller slewing bearing under the axial force

图3 轴向力和倾覆力矩联合作用下三排滚柱式转盘轴承的载荷分布Fig.3 Load distribution of three-row roller slewing bearing under the combined action of axial force and tilting moment
1.2 非线性弹簧单元等效模拟
三排滚柱式转盘轴承中含有大量滚子-滚道接触对,且滚子与滚道间的接触情况复杂。此外,分析非线性接触问题时还可能出现计算不收敛或计算耗时过长等情况。因此,须对滚子-滚道接触模型进行简化,从而提高计算效率。在本文分析中,采用非线性弹簧单元来模拟滚子。通过将滚子与滚道在载荷作用下的接触变形关系赋予非线性弹簧单元,以使弹簧单元可用于表征滚子与滚道之间的接触特性。根据赫兹接触理论,滚子与滚道在载荷作用下的接触变形关系可表示为[9]:

式中:Q为载荷,N;L为滚子长度,mm;δ为滚子与滚道的总变形量,mm。
将滚子与滚道在载荷作用下的接触变形关系简化为:

式中:k为接触刚度,N/mm。
根据式(4)计算得到三排滚柱式转盘轴承滚子的变形量—载荷曲线,如图4所示。由图4可知,滚子的变形量与其承受的载荷之间呈非线性关系,即不能将非线性弹簧单元的刚度直接定义为常数,而是应该将图4所示的接触变形关系赋予非线性弹簧单元,以实现对三排滚柱式转盘轴承滚子-滚道接触特性的准确模拟。文献[16]指出,弹簧的数量会对计算结果造成影响,为保证建模效率和计算精度,采用2根弹簧代替1个滚子的建模方法是最佳的。因此,本文采用1对非线性弹簧单元来模拟三排滚柱式转盘轴承的滚子,如图5所示。
1.3 有限元模型构建
考虑到三排滚柱式转盘轴承为对称结构,为了提高计算效率,只构建一半的转盘轴承有限元模型,其中1个实体滚子简化成1对非线性弹簧单元。在后续分析中,为便于观察各个滚子承受的载荷,按顺时针方向对非线性弹簧单元进行编号,如图6所示。

图4 三排滚柱式转盘轴承滚子的变形量—载荷曲线Fig.4 Curve of deformation-load of roller of three-row roller slewing bearing

图5 三排滚柱式转盘轴承滚子-滚道接触模型Fig.5 Contact model of roller-raceway of three-row roller slewing bearing

图6 三排滚柱式转盘轴承有限元模型Fig.6 Finite element model of three-row roller slewing bearing
建模时考虑三排滚柱式转盘轴承所受的轴向力和倾覆力矩。为了便于施加载荷,在转盘轴承外圈的几何中心设置主节点RP1,并将RP1与外圈滚道上表面进行耦合。由于只构建了一半的三排滚柱式转盘轴承有限元模型,则施加在模型上的载荷为:轴向力Fa=59.5 kN,倾覆力矩M=4.15×105kN·m。在设置边界条件时,将安装基础的下表面定义为完全约束,释放主节点RP1处倾覆力矩方向上的旋转自由度和轴向自由度。
在有限元建模时,划分网格的单元类型和疏密程度会极大地影响计算精度。参考文献[18],选择C3D8R网格单元进行划分。考虑到三排滚柱式转盘轴承的结构尺寸较大,为保证计算精度和减小计算规模,在内、外圈滚道区域采用尺寸为1 mm的网格单元进行划分,其他区域采用尺寸为4 mm的网格单元,如图7所示。此外,由于三排滚柱式转盘轴承中螺栓的数量较多,对螺栓螺纹进行建模会增大建模难度和引发计算收敛问题。因此,将螺纹和螺母的配合等效为绑定约束。根据GB/T5782—2000[19]规定,在螺栓截面上施加170 kN的预紧力;根据VDI 2230[20]的要求,螺栓结合面处摩擦系数设为0.15,如图8所示。

图7 三排滚柱式转盘轴承滚道区域网格划分Fig.7 Mesh generation of raceway area of three-row roller slewing bearing finite element model

图8 螺栓预紧力的施加示意Fig.8 Schematic diagram of application of bolt preload
1.4 结果分析和验证
为了验证中间排滚子对上、下排滚子载荷分布的影响,分别建立了有限元模型1和有限元模型2。其中,模型1忽略了中间排滚子,模型2考虑了中间排滚子。基于2个有限元模型,分析得到三排滚柱式转盘轴承的载荷分布曲线,如图9所示。由图9可知:模型1中上排滚子承受的最大载荷为24 508 N,模型2中上排滚子承受的最大载荷为25 102 N,两者的误差为2.3%;模型1中下排滚子承受的最大载荷为30 129 N,模型2中下排滚子承受的最大载荷为30 678 N,两者的误差为1.7%。结果表明,忽略中间排滚子对计算结果无显著影响,因此下文分析均采用模型1。

图9 三排滚柱式转盘轴承的载荷分布Fig.9 Load distribution of three-row roller slewing bearing
为验证上述有限元模型的准确性,对比由仿真分析和经验公式(1)和(2)计算得到的三排滚柱式转盘轴承上、下排滚子承受的最大载荷,结果如表2所示。由表2可知,上排滚子承受的最大载荷的相对误差为6.15%,下排滚子承受的最大载荷的相对误差为13.00%。相较于有限元仿真结果,由经验公式计算得到的结果偏保守,造成这一现象的原因是经验公式和有限元模型对转盘轴承滚道的假设不同。在经验公式中,转盘轴承滚道被假设为刚性体,在载荷作用下仅滚子产生变形;而在有限元模型中,转盘轴承滚道被假设为具有各向同性的弹性体,在载荷作用下滚子和滚道皆会产生变形。此外,有限元仿真结果中部分数据存在波动,且这些波动出现在载荷较大处,造成这一现象的原因是:有限元模型中滚子与滚道之间以点-点的形式传递载荷,当载荷较大时,滚道的变形增大,导致滚子承受的载荷产生波动。但从总体上看,有限元仿真结果与理论计算结果基本吻合。

表2 三排滚柱式转盘轴承滚子承受的最大载荷的理论值与仿真值对比Table 2 Comparison of theoretical and simulated value of maximum load of rollers of three-row roller slewing bearing
为了进一步验证有限元模型的准确性,对三排滚柱式转盘轴承开展静态加载试验。转盘轴承静态加载试验台如图10所示。三排滚柱式转盘轴承的结构复杂,难以直接测量其滚子的载荷分布情况。因此,通过获取该转盘轴承内侧表面上的应力分布来分析其载荷分布。在三排滚柱式转盘轴承内侧周向布置应变片,如图11所示。在开始试验前,令三排滚柱式转盘轴承低速、平稳运行,使得转盘轴承内部滚子与滚道充分接触;开始试验时,对转盘轴承施加的载荷与有限元仿真时保持一致。通过控制液压缸G1和G2的输出载荷来实现对转盘轴承的施载,施加的轴向力为119 kN,倾覆力矩为8.35×105kN·m。

图10 转盘轴承静态加载试验台Fig.10 Static loading test bench for slewing bearing

图11 三排滚柱式转盘轴承内侧应变片布置Fig.11 Arrangement of strain gauges on the inner side of three-row roller slewing bearing
通过试验测量,获得了三排滚柱式转盘轴承上、下排滚子内圈周向上的应力分布,如图12所示。从总体上看,仿真结果与试验结果基本吻合,但在靠近液压缸G2处(对应的方位角为0°~30°)测得的数据有明显波动,这主要是由贴片处的油孔、粗糙度和锈渍等因素引起的。

图12 三排滚柱式转盘轴承应力分布Fig.12 Stress distribution of three-row roller slewing bearing
为了便于分析仿真结果与试验结果的误差,采用均方根误差(root mean square error,RMSE)[21]来衡量仿真结果与试验结果的误差e,其表达式为:

式中:σsi为应力仿真值,MPa;σti为应力试验值,MPa;i为测点编号;n为测点数量,本文n=18 个。
将相应的数据代入式(5),计算得到三排滚柱式转盘轴承上排滚子周向应力的均方根误差为3.16 MPa,下排滚子周向应力的均方根误差为3.78 MPa。与文献[21]结果对比表明,所得误差在可接受范围内。综上,联合经验公式理论计算结果和静态加载试验结果,验证了所构建有限元模型的准确性。
2 紧固螺栓对转盘轴承载荷分布的影响
转盘轴承通常以螺栓连接的方式固定在支承结构上,紧固螺栓的预紧力及其结合面处的摩擦系数会影响转盘轴承的整体刚度,从而影响其载荷分布。为此,基于上文构建的有限元模型,分别考察螺栓预紧力及其结合面处摩擦系数对三排滚柱式转盘轴承载荷分布的影响,旨在为转盘轴承的工程应用提供参考和借鉴。
2.1 不同螺栓预紧力下的载荷分布
130.20.1005型三排滚柱式转盘轴承的外圈为动圈,内圈为固定圈,内圈通过螺栓固定在安装基础上。为保证转盘轴承装配体结构的刚性和连接紧固性,须对紧固螺栓施加预紧力。但由于预紧力施加方法不同,使得实际预紧力大小与目标加载值间存在误差,从而影响转盘轴承的载荷分布。为了分析螺栓预紧力对三排滚柱式转盘轴承载荷分布的影响,在其有限元模型中对螺栓施加不同的预紧力,分析不同预紧力下该转盘轴承的载荷分布情况。
分别对三排滚柱式转盘轴承有限元模型中的螺栓施加0,100和170 kN预紧力,通过有限元分析得到该转盘轴承的载荷分布,如图13所示。由图13所示的载荷分布曲线可以看出,随着螺栓预紧力的增大,承受载荷的滚子数量发生变化。在上排滚子中,承受载荷的滚子数量随着预紧力的增大而增多,而下排滚子则相反。此外,如图14所示,三排滚柱式转盘轴承上、下排滚子在不同螺栓预紧力作用下承受的最大载荷不同。当螺栓预紧力从0 kN分别增大到100 kN和170 kN时,上排滚子承受的最大载荷分别增大3.9%和11.4%,下排滚子承受的最大载荷分别减小13.7%和18.9%。由此可知,螺栓预紧力对三排滚柱式转盘轴承的下排滚子载荷分布的影响较大。

图13 不同螺栓预紧力下三排滚柱式转盘轴承的载荷分布Fig.13 Load distribution of three-row roller slewing bearing under different bolt preloads

图14 不同螺栓预紧力下三排滚柱式转盘轴承的最大载荷Fig.14 Maximum load of three-row roller slewing bearing under different bolt preloads
2.2 螺栓结合面处不同摩擦系数下的载荷分布
紧固螺栓与转盘轴承结合面处的摩擦系数受制造工艺、结合面处清洁度和氧化物等因素的影响。基于上文构建的有限元模型,考察螺栓结合面处不同摩擦系数对转盘轴承载荷分布的影响。在三排滚柱式转盘轴承有限元模型中,设置不同的螺栓结合面处摩擦系数(0.05,0.10 和0.15),通过有限元分析得到该转盘轴承的载荷分布,如图15所示。
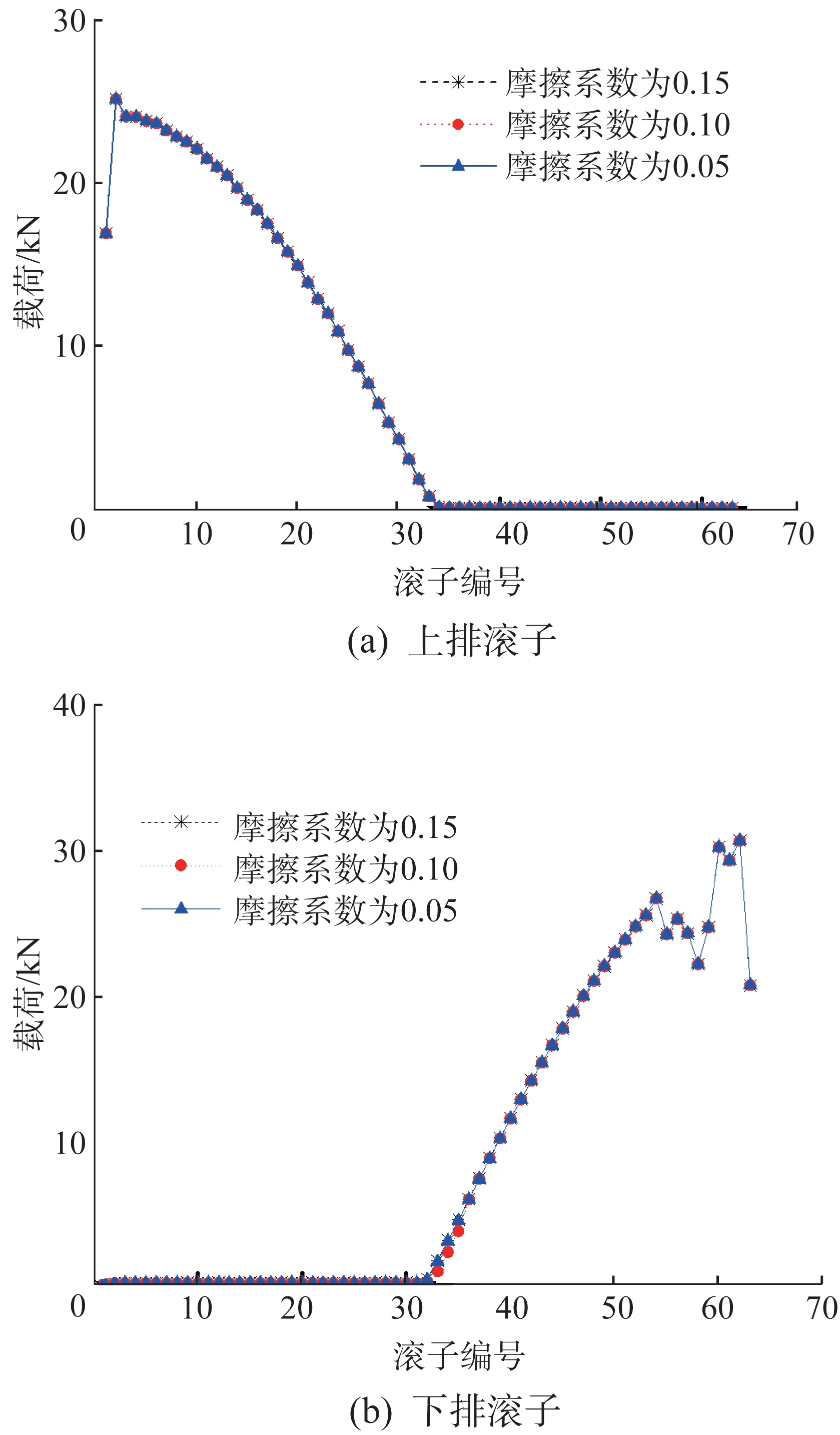
图15 螺栓结合面处不同摩擦系数下三排滚柱式转盘轴承的载荷分布Fig.15 Load distribution of three-row roller slewing bearing under different friction coefficients of bolt joint surface
从图15中可以看出,在不同的螺栓结合面处摩擦系数下,三排滚柱式转盘轴承的载荷分布曲线重叠在一起,3条曲线之间的差异很小。螺栓结合面处不同摩擦系数下三排滚柱式转盘轴承的最大载荷如图16所示。与螺栓预紧力对转盘轴承载荷分布的影响不同,螺栓结合面处摩擦系数对转盘轴承的载荷分布几乎没有影响。

图16 螺栓结合面处不同摩擦系数下三排滚柱式转盘轴承的最大载荷Fig.16 Maximum load of three-row roller slewing bearing under different friction coefficients of bolt joint surface
3 结 论
通过有限元方法,建立了考虑紧固螺栓的三排滚柱式转盘轴承有限元模型。建模时通过非线性弹簧单元的等效处理,减小了运算规模,使得在普通计算机上也能实现对转盘轴承载荷分布的求解。同时,通过转盘轴承的静态加载试验验证了有限元模型的准确性。
结果表明:在紧固螺栓的工作参数中,螺栓预紧力对三排滚柱式转盘轴承载荷分布的影响显著,而螺栓结合面处摩擦系数的影响微弱;当螺栓预紧力增大时,上排滚子承受的最大载荷随之增大,而下排滚子承受的最大载荷显著减小;在轴向力和倾覆力矩的联合作用下,下排滚子承受的载荷总体上高于上排滚子,则增大螺栓预紧力有利于提高三排滚柱式转盘轴承的承载能力。在转盘轴承的安装和后期维护中,应当保证充足的螺栓预紧力,避免因螺栓预紧力不足而导致轴承提前失效。

