考虑压力与温度影响的螺杆马达过盈量设计方法
钟良春,况雨春,舒 峰,张 聪
(1.西南石油大学机电工程学院,四川 成都 610500;2.中建环能科技股份有限公司,四川 成都 610500)
螺杆钻具广泛应用于各个行业。马达作为其核心部件,常在高温、高压和高应力循环的恶劣条件下工作[1-3]。为使螺杆钻具能够在恶劣条件下正常工作并保证其使用寿命,合理设计马达定子与转子之间的过盈量十分必要。
Ba等[4]提出了一种新的螺杆马达设计与测试方法,但并未考虑实际工况下螺杆马达过盈量的变化。曹刚等[5]建立了螺杆泵的三维有限元模型,并采用单向解耦方法分析了过盈量对其定子温度场的影响。柳欢欢和郑道宽[6-7]通过建立螺杆马达的三维流固耦合模型,分析了马达输出扭矩与过盈量的关系。Alvarez等[8]预测了螺杆马达在工作过程中的过盈量变化情况,并分析了过盈量对马达工作性能的影响。
目前,螺杆马达过盈量的设计大多根据经验展开。笔者提出一种考虑工作压力和井下温度的螺杆马达过盈量设计方法,并通过螺杆钻具整机台架试验来验证所提出方法的可行性,旨在为螺杆马达过盈量以及其余参数的设计提供参考。
1 螺杆马达有限元模型及参数
以4-5头普通内摆线马达为例,建立其定子与转子的二维啮合有限元模型,如图1所示。其中:定子的材料为丁腈橡胶,转子的材料为镀铬合金钢,在建模时将转子视作刚体处理。该螺杆马达定子的大、小径分别为:Rs=101.88 mm,rs=74.76 mm,定子的最小厚度d=15 mm。转子的大、小径分别为:Rr=90 mm,rr=60 mm。
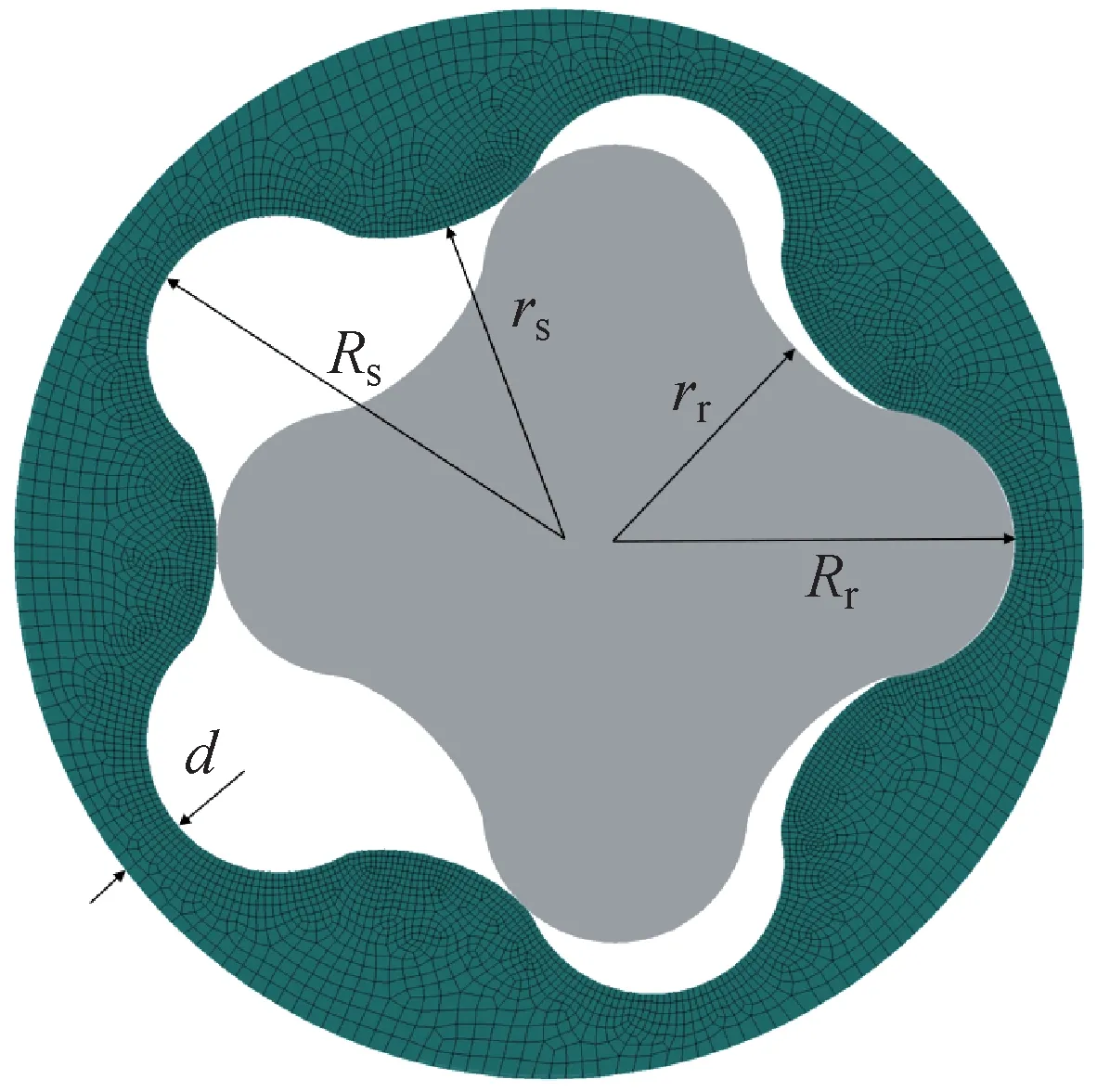
图1 螺杆马达定子与转子的二维啮合有限元模型Fig.1 Two-dimensional meshing finite element model of stator and rotor of screw motor
橡胶作为一种超弹性材料,具有高度非线性和几乎不可压缩等特征。常用的橡胶材料本构模型包括Ogden 模型、Mooney-Rivlin(M-R)模型和Yeoh 模型[9-11]。鉴于螺杆马达中定子的变形小于150%,选择M-R模型。
M-R模型的一般形式为:

式中:W为应变能密度函数;Cij为材料常数;I1、I2、I3分别为材料的第一、第二和第三应力不变量;k为体积模量。
当N=1 时,上述模型即为常用的两参数模型。假定橡胶为不可压缩材料,则其M-R模型可表示为:

根据橡胶材料的硬度Hr与弹性模量E0的试验值[12-13]以及计算得到的C10、C01,通过拟合可得:

通过硬度计测得丁腈橡胶试样的邵氏硬度为75,联立式(3)和式(4)可得C01/C10=0.015,则丁腈橡胶的本构参数为:C10=1.302,C01=0.020。
2 压力和温度对螺杆马达过盈量的影响
2.1 压力的影响
对螺杆马达二维有限元模型的内腔表面施加20 MPa 的均匀压力,暂不考虑温度的影响,通过仿真计算得到其定子的位移云图,如图2所示。由图2可以看出,螺杆马达定子小径处(即橡胶层较厚处)的变形大,大径处(即橡胶层较薄处)变形小;定子截面的结构对称,其位移均沿圆周方向呈周期性变化,最大位移位于定子大径处,为0.18 mm,小径处的位移为0.1 mm。在该工况下,若要保证螺杆钻具正常工作,即确保其马达的各个密封腔之间不互相串通、泄漏(螺杆钻具正常工作时允许一定的泄漏存在),则要保证马达的过盈量大于0.28 mm。

图2 20 MPa均匀压力下螺杆马达定子的位移云图Fig.2 Displacement nephogram of screw motor stator under 20 MPa equalizing pressure
在螺杆钻具钻进过程中,不同井段的工作压力不同。分别取均匀压力为20,30,40和50 MPa,对不同均匀压力下螺杆马达的定子进行仿真分析,得到其位移变化曲线(因定子截面的结构对称,仅取1/10定子进行分析),如图3所示。由图3可以看出,不同压力下螺杆马达定子位移的变化规律基本相同,但随着压力的增大,定子大径与小径处的位移差越来越大,即压力越大,定子变形程度越大。当压力达到50 MPa时,定子大、小径处的位移差达到了0.24 mm,由此可知传统的均匀过盈量设计方法是不合理的。

图3 不同均匀压力下螺杆马达定子的位移变化曲线Fig.3 Displacement curves of screw motor stator under different equalizing pressures
此外,由于螺杆马达内各个密封腔的压力不同,不同腔室之间会相互挤压,从而导致定子产生变形。根据螺杆马达定子与转子的啮合关系,选择极限啮合位置,此时定子与转子之间形成了5个密封腔,如图4所示。从螺杆马达的入口处到出口处,工作压力逐级降低,这也是螺杆钻具使用一段时间后出现“喇叭口”的重要原因。因此,第1级螺杆马达定子的变形最大且最易失效,则只须取第1级螺杆马达的截面作为研究对象,即可确定整个马达的过盈量。假定螺杆马达入口处的工作压力为20 MPa,定子与转子的单级工作压差为0.60 MPa,转子按顺时针方向转动。随着转子的转动,腔室面积减小的密封腔为排出腔且为增压腔。第1级螺杆马达截面处有5个密封腔,其中腔室1,2为排出腔,腔室4,5为吸入腔。对各腔室加载的压力如下:对腔室1加载20.60 MPa压力,对腔室2加载20.45 MPa压力,对腔室3加载20.30 MPa压力,对腔室4 加载20.15 MPa 压力,对腔室5 加载20.00 MPa压力。
在压差作用下螺杆马达定子的Mises 应力及位移云图分别如图5和图6所示。从图5中可以看出,应力集中主要出现在啮合点A附近,位于A点高压侧的交界点处,最大Mises应力为0.372 MPa,说明该处最易磨损[14-16]。从图6中可以看出,在啮合点附近,高压侧橡胶明显被挤向低压侧,定子最大变形也出现在啮合点A的高压侧,这是因为高压腔室1与低压腔室5 的工作压差为0.60 MPa,且A点处的橡胶层最厚。压差作用下螺杆马达定子位移的变化曲线如图7所示。从图7中可以看出,在最大压差的两侧(即廓线相角为36°处),定子的最大位移达到了0.977 mm。

图4 螺杆马达密封腔二维模型(处于极限啮合位置)Fig.4 Two-dimensional model of screw motor seal cavity(in the limit meshing position)

图5 压差作用下螺杆马达定子的Mises应力云图Fig.5 Mises stress nephogram of screw motor stator under the action of pressure difference

图6 压差作用下螺杆马达定子的位移云图Fig.6 Displacement nephogram of screw motor stator under the action of pressure difference
2.2 温度的影响
在钻井工作中,钻井液循环使用。因黏性滞后及摩擦而产生的热量可被不断循环使用的钻井液带走。本文在采用有限元仿真分析温度对螺杆马达定子的影响时忽略了该因素,即视井下温度场为均匀温度场且不考虑压力的影响。
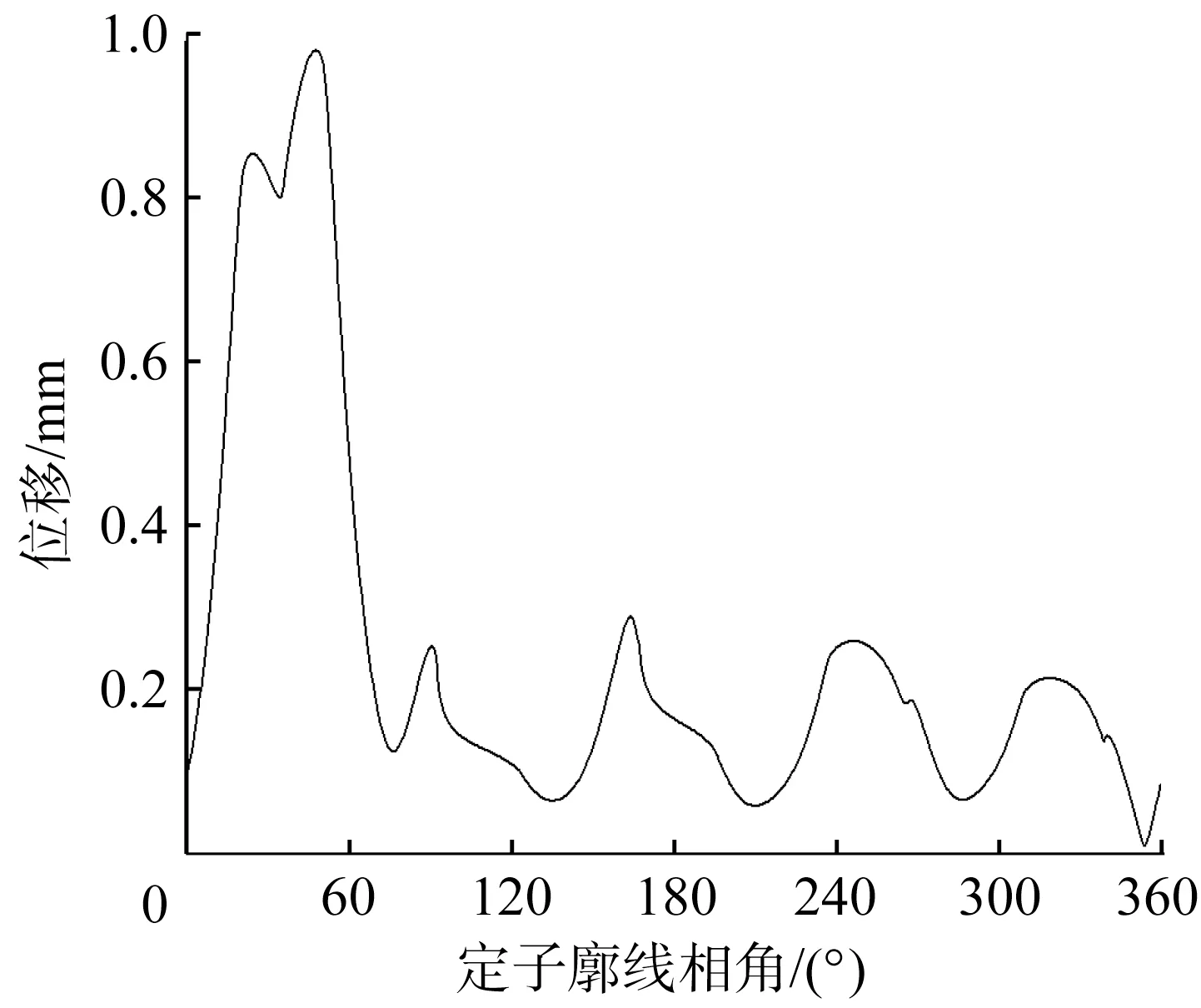
图7 压差作用下螺杆马达定子的位移变化曲线Fig.7 Displacement curve of screw motor stator under the action of pressure difference
在对螺杆马达定子的温度场进行有限元分析时,作如下基本假设:1)橡胶的材料参数和热力学参数不随温度变化;2)定子与转子在轴向上没有热传导作用(即马达轴向上无温度梯度)。因此,螺杆马达定子的三维热分析问题可简化为二维平面热分析问题。
在考虑热效应后,弹性体的正应变分为两部分:1)因温度改变,弹性体内各点自由膨胀(或自由收缩)所引起的正应变ε(T);2)弹性体内各部分之间的相互约束所引起的正应变ε(S)。则弹性体的总正应变ε可表示为:

正应变ε(T)具有各向同性的(为相似应变),即同一点在每个方向上产生的压缩和伸长线应变相等,且不存在切应变。若温度变化量为ΔT,弹性体的热膨胀系数为α,在二维平面中,则有:

正应变ε(S)与由温度引起的应力之间服从Hooke定律,可表示为:

则热弹性体的本构方程为:

其中:

式中:σx、σy分别为x、y方向的总正应力;εx、εy分别为x、y方向的总正应变;τxy为总切应力;γxy为总切应变。
由上述本构方程可知,温升对热弹性体的正应力有影响,对其切应力无影响。设螺杆马达定子的初始温度为20 ℃,某井段的温度为50 ℃。基于上述本构方程,将井下温度作为螺杆马达有限元模型单元节点处的载荷并进行仿真分析,得到其定子的Mises 应力和位移云图,分别如图8 和图9 所示。从图8 和图9 中可以看出,螺杆马达定子小径处的应力小、位移大,大径处的应力大、位移小;当温度为50 ℃时,定子的最大Mises 应力为0.026 MPa,最大位移为0.096 mm。

图8 温度为50 ℃时螺杆马达定子的Mises应力云图Fig.8 Mises stress nephogram of screw motor stator with temperature of 50 ℃

图9 温度为50 ℃时螺杆马达定子的位移云图Fig.9 Displacement nephogram of screw motor stator with temperature of 50 ℃
在螺杆钻具钻进过程中,不同井段的温度不同。分别取井下温度为50,60,70,80 和90 ℃,对螺杆马达定子进行仿真分析,提取其位移变化曲线,如图10所示。由图10可以看出,在不同温度下,螺杆马达定子位移的变化规律基本相同,橡胶层越厚处的位移越大;随着温度的升高,定子大、小径处的位移差增大,即温度越高定子的变形越大;当温度为90 ℃时,定子大、小径处的位移差为0.26 mm。

图10 不同温度下螺杆马达定子的位移变化曲线Fig.10 Displacement curves of screw motor stator under different temperatures
3 螺杆马达过盈量及定子廓线设计
3.1 过盈量设计
过盈配合是为了使螺杆马达定子和转子之间形成连续独立的密封腔,并具有一定承压能力,从而可将钻井液的液压能转化为机械能。因此,螺杆马达的过盈量必须合理设计,否则会影响螺杆钻具的工作性能。1)过盈量偏大会导致马达转子和定子之间的接触应力和摩擦扭矩增大,从而加速定子的疲劳损坏,缩短螺杆钻具的使用寿命;2)过盈量偏小会导致螺杆钻具的承压能力偏弱,从而导致其工作效率降低。
由密封性能评价准则可知[17]:当螺杆马达定子与转子的接触应力大于相邻腔室的压差时,两腔室间实现密封,反之则泄漏。以密封性能评价准则为基础,对螺杆马达的过盈量进行合理设计。假设螺杆马达转子作理想的行星运动,忽略其动力学因素,分别选取过盈量为0.2,0.3,0.4,0.5和0.6 mm,对不同过盈量下定子与转子的接触应力进行有限元仿真分析。当螺杆马达处于极限啮合位置时,不同过盈量下其定子与转子的接触应力如表1所示。
若螺杆马达定子与转子啮合的危险截面(即图4所示截面)满足密封条件,则其他截面也满足。由于螺杆马达危险截面的A点为线接触,在压差作用下,定子产生较大的变形,导致该点处的接触应力增大,从而达到密封条件,而其余各点均为点接触,因压差变形而增大的接触应力较小,只有接触应力达到0.60 MPa才可实现密封。由表1中可知,只有当过盈量不小于0.5 mm时,螺杆马达才能达到密封条件。

表1 不同过盈量下螺杆马达定子与转子的接触应力(处于极限啮合位置)Table 1 Contact stress between stator and rotor of screwmotor under different interference(in the limit meshing position)
当螺杆马达转子的公转角为0°时,定子与转子的线密封长度最长,均匀接触使得定子与转子的接触应力最小,如图11所示。

图11 过盈量为0.5 mm、转子公转角为0°时螺杆马达定子与转子的接触应力分布Fig.11 Contact stress distribution of stator and rotor of screw motor with interference of 0.5 mm and rotor common angle of 0°
对于常规螺杆钻具而言,在相同过盈量下其马达定子大、小径处的接触应力不同,小径处的接触应力必然小于大径处。基于此,提出螺杆马达定子大、小径处采用不同过盈量的设计方法,在保证密封性的同时尽可能使大、小径处的接触应力均衡。经过对不同过盈量组合下的螺杆马达进行有限元仿真分析发现,当定子大径处过盈量为0.2 mm,小径处过盈量为0.5 mm,大、小径间过盈量采用线性插值时,定子与转子之间既能实现密封,又能良好地接触。不同过盈量设计方法下螺杆马达定子与转子的最大接触应力和Mises 应力分别如图12 和图13 所示。由图12 和图13 可以看出,相较于过盈量均匀设计(过盈量为0.5 mm)的螺杆马达,过盈量非均匀设计的螺杆马达的定子与转子的最大接触应力整体减小,减小了0.115 MPa,最大接触应力的平均值由0.904 MPa 减小为0.813 MPa,减小了10.1%,这在一定程度上减轻了定子的接触磨损。同时,定子的最大Mises应力在整体上也有所减小,最大Mises 应力的平均值由1.106 MPa 减小为0.980 MPa,减小了11.2%,这可使定子处的挤压、剪切作用有所减轻,在一定程度上降低了定子的疲劳损坏速度。

图12 不同过盈量设计方法下螺杆马达定子与转子的最大接触应力变化曲线Fig.12 Maximum contact stress curves of stator and rotor of screw motor under different interference design methods

图13 不同过盈量设计方法下螺杆马达定子的最大Mises应力变化曲线Fig.13 Maximum Mises stress curves of screw motor stator under different interference design methods
3.2 定子廓线设计
在压差作用下,螺杆马达危险截面法向位移的波动较大,且不具有周期对称性。若按该法向位移曲线对螺杆马达过盈量进行补偿设计,则在其他截面下定子与转子啮合时会产生较大的接触应力。因此,取压差作用下螺杆马达定子的最大法向位移为临界值,按照均匀压力作用下定子的法向位移曲线,对螺杆马达的过盈量进行设计。假设均匀压力作用下螺杆马达定子的最大法向位移为s1,压差作用下定子的最大法向位移为s2,将均压作用下定子的预补偿量放大s2/s1倍,此时处于危险截面的定子与转子也能实现有效密封。在某一特定井段内,必然同时存在压力和温度的影响,对此工况下螺杆马达的过盈量进行设计时,假设压力与温度对螺杆马达定子廓线的影响是相互独立的,耦合压力和温度这2种因素引起的变形量,得到所需的定子廓线,如图14所示,其原点为定子的形心。

图14 考虑不同影响因素时螺杆马达定子的廓线对比Fig.14 Comparison of stator profiles of screw motor considering different influence factors
4 试验验证
某公司试制的6根螺杆钻具马达的过盈量设计方法如表2所示。通过螺杆钻具整机台架试验(试验现场如图15 所示),获得螺杆马达的性能曲线,如图16和图17所示。同时,根据试验数据,采用参考文献[18]中的公式,计算得到螺杆马达的总效率与压降的关系,如图18所示。

图15 螺杆钻具整机台架试验现场Fig.15 Bench test site of screw drilling tool
由图16至图18可知:
1)在相同压降下,过盈量非均匀设计的螺杆马达的总效率较过盈量均匀设计的螺杆马达低,这是因为过盈量非均匀设计仅为了改善定子与转子的接触,延长其使用寿命。
2)6个螺杆马达的转速均随压降的增大而下降,其中PDM1和PDM4的过盈量最小,密封性能较差,转速下降最快,总效率也最低;PDM2 和PDM5 在设计时补偿了压力对过盈量的影响,其转速最为稳定,总效率也最高;PDM3和PDM6在设计时考虑了压力和温度的影响,其过盈量较小,但因试验在常温下展开,故其转速下降得比PDM1和PDM4快,总效率也比PDM1和PDM4低。

表2 6个螺杆马达的过盈量设计方法Table 2 Interference design methods for six screw motors
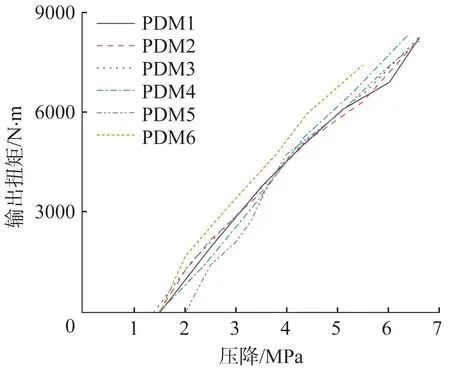
图16 螺杆马达输出扭矩随压降的变化曲线Fig.16 Change curves of output torque of screw motor with pressure drop

图17 螺杆马达转速随压降的变化曲线Fig.17 Change curves of rotating speed of screw motor with pressure drop
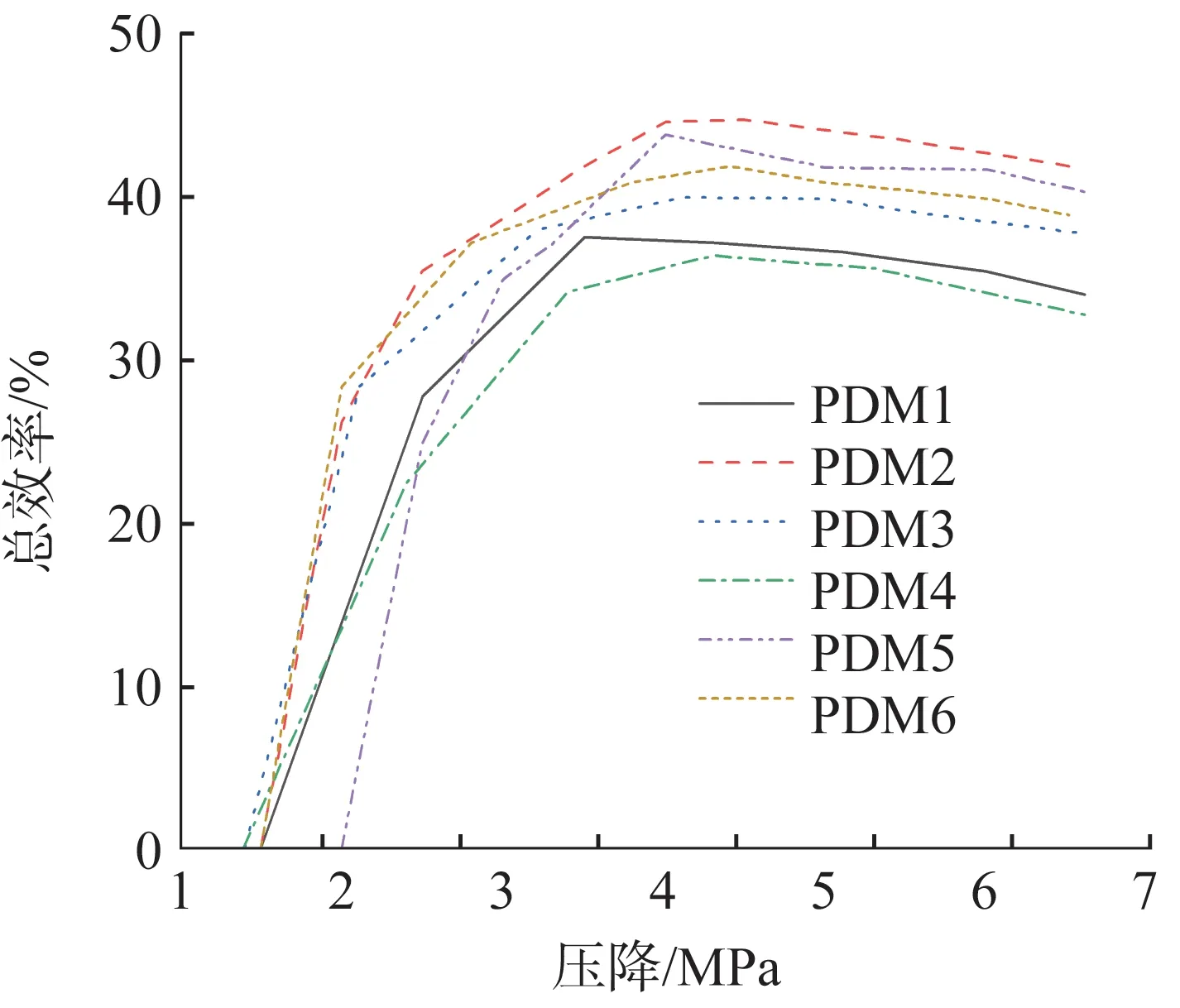
图18 螺杆马达总效率随压降的变化曲线Fig.18 Change curves of total efficiency of screw motor with pressure drop
5 结 论
本文通过建立螺杆马达定子与转子的二维啮合有限元模型,以转子为基准,考虑压力和温度对马达过盈量的影响,提出了一种过盈量非均匀设计的方法,并通过螺杆钻具整机台架试验验证了有限元结果的准确性,得到如下结论。
1)螺杆马达过盈量均匀设计会使其定子与转子的接触应力过高,而采用过盈量非均匀设计方法可改善定子的受力状况。相较于过盈量为0.5 mm的螺杆马达,大径处过盈量为0.2 mm、小径处过盈量为0.5 mm 的螺杆马达的定子与转子的最大接触应力的平均值由0.904 MPa 减小至0.813 MPa,减小了10.1%;定子的最大Mises 应力的平均值由1.106 MPa减小至0.982 MPa,减小了11.2%。
2)考虑压力和温度的过盈量非均匀设计方法可使螺杆马达的效率得到有效提升。
综上,所提出的过盈量非均匀设计方法及试验数据为螺杆马达过盈量及其余参数的设计提供了参考。

