基于多源融合理论的机床圆度误差测量不确定度评定

付 扬，李国龙，徐 凯，唐晓东

（重庆大学机械传动国家重点实验室，重庆 400044）

数控机床是推动制造业发展的重要智能装备之一。随着精密制造技术的发展，对数控机床制造精度的要求越来越高。机床自身的精度在很大程度上决定了工件的最终加工精度。圆度（通常称为圆度误差）是评价机床综合精度的重要指标之一。为满足精密零件的加工要求，必须对机床的精度等级进行准确评定［1］。通常情况下，机床的精度须采用精密仪器来测量。测量准确度是衡量测量结果可信度的基本指标，在实际工程中常用测量不确定度来表示。常见的测量不确定度评定方法因要实现广泛应用，故评定过程复杂且不具有针对性。因此，针对某一特定对象提出可靠而实用的测量不确定度的评定方法是一个亟待解决的问题。鉴于数控机床在工业生产中应用广泛，对其圆度误差测量不确定度评定方法进行研究，不仅可为提高机床精度奠定基础，而且对提升其加工质量和生产效率具有重要意义。

国内外许多学者对零部件圆度误差的评定方法进行了研究，主要包括最小二乘法（least sqaure method，LSM）［2］、最小区域圆（minimum zone circle，MZC）法［3］、最大内切圆（maximum inscribed circle，MIC）法［4］和最小外接圆（minimum circumscribed circle，MCC）法［5］。王东霞等［6］采用三坐标测量机测量了工件的圆度误差，并利用蒙特卡洛法（Monte Carlo method，MCM）对工件圆度误差的测量不确定度进行了评定；Chiabert 等［7］基于GPS（global positioning system，全球定位系统）标准，通过比较概率统计方法与经典的LSM 来评定工件的圆度误差及其不确定度；Huo等［8］提出了一种多级搜索算法，可快速、准确地评定最小区域的圆度误差；Srinivasu等［9］提出了一种基于LSM和新型概率全局搜索洛桑技术的混合方法，可准确评定工件的圆度误差。

目前，较成熟且应用较广泛的不确定度评定方法主要有GUM（Guide to theevaluation and expression of uncertainty in measurement，《测量不确定度评定和表示》指南）法［10］和MCM［11］。蒋薇等［12］对GUM 法进行了扩展，提出了一种更一般化的用于测量不确定度评定和表示的随机模糊变量（random fuzzy variables，RFVs）法；朱大业等［13］采用MCM实现了鞭打试验测量不确定度的评定，得到了可靠的复杂非线性系统试验不确定度评定方法；王汉斌等［14］基于新一代GPS的产品检验标准，借助黑箱模型，提出了一种符合性不确定度评定方法；Ding等［15］分析了双球杆安装误差对测量不确定度的影响，提出通过单轴驱动和安装参数优化的方式来减小已识别误差的不确定度；Lee等［16］使用双球杆测量了机床旋转轴的偏移误差和垂直度误差，并分析了测量结果的标准不确定度；Barini等［17］从模型偏差、重现性和测量不确定度等方面对复杂表面测量过程中不确定因素的来源和影响进行了分析，并用统计分析方法计算了测量不确定度。

综上所述，目前关于圆度误差测量不确定度的研究主要针对机械零部件，而对机床主轴圆度误差及其测量不确定度的研究极少。此外，现有的不确定度评定方法具有一定的局限性，难以直接将其应用于机床圆度误差测量不确定度的评定。主要原因在于：GUM 法须对所有不确定度的贡献因素进行分布估计，同时还须对测量模型中各因素之间的相关性进行考察［18］；MCM 是一种基于GUM 法和概率分布传播理论的不确定度评定方法，其评定精度较高，但评定结果存在一定的概率性。

针对上述问题，笔者提出了一种基于多源融合理论的机床圆度误差测量不确定度评定方法。利用球杆仪对某加工中心ZX平面的圆度误差进行测量，并考虑测量过程中所有不确定度的贡献因素，根据黑箱理论构建机床圆度误差测量不确定度评定模型，以避免对输入量与输出量之间函数关系的求解，在克服结果概率性的情况下完成对机床圆度误差测量不确定度的评定。

1 圆度误差评定

圆度误差是指机器沿数据采集弧运动时测量设备记录的最大半径与最小半径之间的差值［19］。采用球杆仪测量机器圆度误差时，先基于测量端点的相位角和半径绘制实际圆轨迹，再与理想圆轨迹进行对比并计算得到圆度误差。本文基于LSM构建圆度误差评定模型。

1.1 整圆圆度误差评定模型

如图1 所示，假定某圆截面上的测量点Pt=（xt，yt），t=1，2，…，n，其中n表示球杆仪的测量点数。图中：rt为测量点Pt相对原点O的半径；C为最佳拟合圆心O1与原点O的距离；θt为测量点Pt相对原点O的相位角；α为最佳拟合圆心O1相对原点O的偏心角；r′t为测量点Pt相对最佳拟合圆心O1的半径。利用LSM 评定其圆度误差，在直角坐标系中建立如下模型：

图1 圆轨迹偏心示意Fig.1 Schematic diagram of circular track eccentricity

假设所有测量点均匀分布，可得出最佳拟合圆心(a，b)和最佳拟合半径r，分别为：

1.2 非整圆圆度误差评定模型

为不失一般性，本文建立适用于非整圆的圆度误差评定模型。设圆的一般方程为：

式中：e、d、g均为常数。

基于各测量点的坐标来拟合理想圆，令εt=++ext+dyt+g。首先，根据LSM，基于式（4）求解e、d、g的值。

则在理想圆坐标系中，实际圆弧的半径r′t为：

确定r′t的最大值r′tmax和最小值r′tmin后，即可得到圆度误差。

2 多源融合误差测量不确定度评定方法

圆度误差通常由多种因素造成，这种由多种因素造成的误差称为多源融合误差，目前尚无可靠的方法来评定其测量不确定度。本文根据误差的累积性和传递性，提出一种多源融合误差测量不确定度评定方法。

2.1 多源融合误差测量不确定度评定理论

在精度测量实验中，很多被测量都是通过间接测量得到的，即通过合成多个对其有影响的直接测量量的测量结果来得到最终值。在这种情况下，多源融合误差根据Zadeh的扩展原理（Zadeh’s extension principle，ZEP）［20］来传递测量不确定度。ZEP的表达式为：

式中：Z=f(w，v)，表示被测量Z为关于其影响因素w和v的函数。

从计量角度来看，根据直接测量量的联合可能性分布情况，得到被测量的分布函数。不确定度作为精度测量值的组成部分，其以某种形式跟随直接测量量进行传递和累积，形成被测量的总不确定度。

2.2 多源融合误差测量不确定度评定模型

多源融合误差测量不确定度评定问题是一个多因素、多层次的综合问题。通常情况下，多源融合误差包含的贡献因素较多，且这些贡献因素与被测量的函数关系难以求得。因此，多源融合误差测量不确定度的评定是一个极其繁杂的过程。本文基于文献［20］中的黑箱理论，建立了多源融合误差测量不确定度评定模型。

在评定多源融合误差测量不确定度前，应将测量过程模型化，即建立被测量Z与其贡献因素之间的函数关系：

式中：X为各贡献因素的测量结果合成值；Th为各贡献因素的修正值。

基于测量结果合成的标准不确定度的一般性公式为：

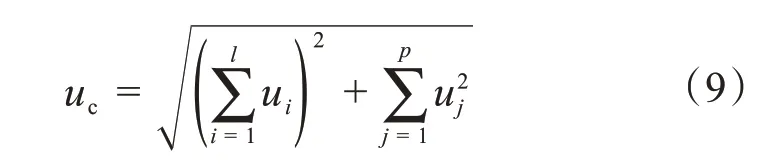
式中：l为强相关的不确定度贡献因素的个数；p为不相关的不确定度贡献因素的个数。

在黑箱模型中，若已知某些不确定度贡献因素之间相关，但相关性系数未知，则保守的做法是假定其强相关。

在几何误差测量过程中，测量结果的准确度仅通过测量仪器示值来评判，但测量仪器示值通常只能反映被测系统在运行过程中对测量结果有影响的因素，而并未反映外界环境因素的影响。因此，在分析不确定度的贡献因素时，应考虑环境因素和人员因素，且通常假定各环境因素和人员因素为不相关因素。在考虑环境因素和人员因素的条件下，基于测量结果合成的标准不确定度为：

式中：q为对不确定度有贡献的环境因素和人员因素的个数。

3 机床圆度误差测量不确定度评定

3.1 机床圆度误差不确定度评定体系

基于球杆仪测量得到的机床圆度误差是典型的多源融合误差，须根据测量过程准确分析其不确定度的来源，以保证评定结果的可靠性。实践表明，球杆仪测量系统所包含的圆度误差的贡献因素达10项，此外还包括5项环境因素和人员因素，且这些贡献因素与圆度误差测量值的函数关系难以求得。从机床精度测量的误差属性出发，建立其圆度误差测量不确定度评定体系，如图2所示。

3.2 机床圆度误差测量不确定度评定模型

为保证机床圆度误差测量结果的可靠性，采用多次重复测量策略，即在重复性条件下对机床圆度误差进行m次独立的测量实验。以机床圆度误差γ的算术平均值-γ为最佳估计值，采用Bessel公式计算实验测量结果的标准差s()，得到A类标准不确定度，其评定模型为：

图2 机床圆度误差测量不确定度评定体系Fig.2 Evaluation system of machine tool roundness error measurement uncertainty

在机床圆度误差测量过程中，球杆仪测量系统会显示10项圆度误差的贡献因素，并以百分比形式列出其所占比重。在保守条件下，假设各贡献因素的相关系数为1。基于球杆仪测量系统的机床圆度误差测量不确定度为：

式中：λi、λj分别为强相关、不相关贡献因素在圆度误差中所占的比重。

4 实例验证

采用QC20-W型号无线球杆仪对某加工中心ZX平面的圆度误差进行测量。本次实验采用部分圆检测，起始角和终止角分别为250°和110°，球杆仪测量杆的长度为100 mm。在开始测量前，对该加工中心进行预热直至达到稳定状态；整个测量过程耗时30 min，温度变化不超过2 ℃；球杆仪在使用前用校准规进行校准。基于球杆仪的某加工中心ZX平面圆度误差的测量现场如图3所示。

4.1 机床圆度误差测量及评定结果

为尽可能提高机床圆度误差测量的准确度，共进行12 次测量实验，每组采样点为220 个。该加工中心ZX平面圆度误差的测量结果如图4所示。

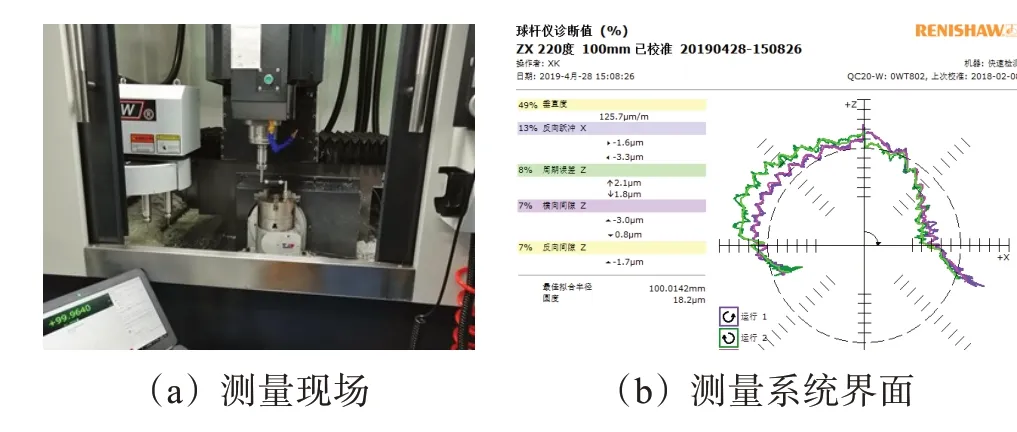
图3 某加工中心ZX平面圆度误差测量现场Fig.3 Measurement site of ZX plane roundness error of a machining center

图4 某加工中心ZX平面圆度误差测量结果Fig.4 Measurement result of ZX plane roundness error of a machining center

为避免测量过程受偶然性因素的影响，剔除最小值（第4组）和最大值（第12组），取其余10组测量数据的平均值，利用LSM计算对应的圆度误差。表1所示为采样间隔为5°时各采样点的半径变化值Δr。

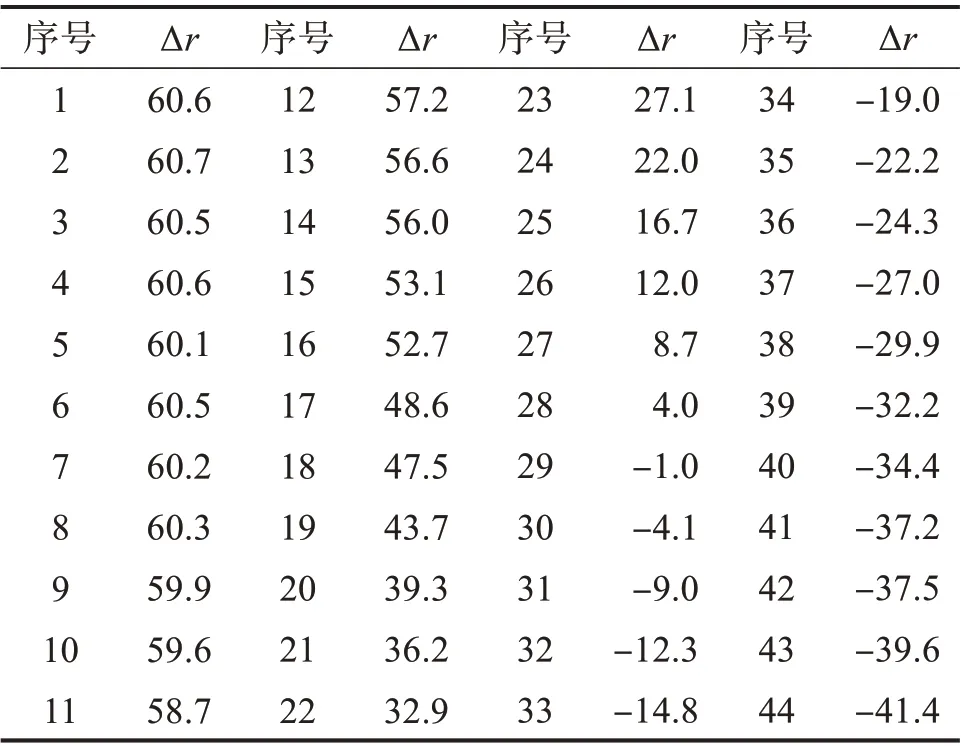
表1 采样间隔为5°时各采样点的半径变化值Table 1 Radius change value of each sampling point with sampling interval of 5°单位：μm

为判定测量结果的正确性，根据非整圆圆度误差评定模型计算上述圆弧的最佳拟合圆心坐标、最佳拟合半径和圆度误差，并比较球杆仪测量结果和评定模型计算结果，如表2所示。结果显示，上述2种方法得到的结果的一致性较好，表明测量结果正确。

表2 某加工中心ZX平面圆度误差测量值与计算值比较Table 2 Comparison of measured value and calculated value of ZX plane roundness error of a machining center单位：μm

4.2 机床圆度误差测量不确定度计算

球杆仪测量系统显示的10 项加工中心ZX平面圆度误差贡献因素的测量结果如表3所示（剩余的10组数据按顺序标号）。需要说明的是，表3中垂直度误差所占的比重超过50%，表明该加工中心的Z轴和X轴在长期使用后已经不垂直且误差较大，但这并不影响对圆度误差测量不确定度的研究。由式（11）计算得到各圆度误差贡献因素的测量不确定度，如表4所示。

假设同名误差项具有强相关性，其他各误差项之间无相关性，由式（13）计算得到球杆仪测量系统显示的所有圆度误差贡献因素的测量不确定度uz=0.828 7 μm。

本实验中所用球杆仪的分辨率小于0.1 μm，根据B 类评定方法，取95%置信概率下的置信因子k=1.96，由式（12）计算得到其测量不确定度urp=0.0510 μm。

由温度引起的不确定度主要由材料的热膨胀系数确定，本实验中校准规在规定温度范围内不会发生膨胀。假设温度服从三角分布，由温度引起的测量不确定度utemp为：

其中：

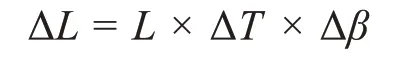
式中：L为球杆仪测量杆长度，μm；ΔT为实际温度与标准温度的差值，°C；Δβ为测量仪器与机床的热膨胀系数差，10-6/°C。

常用的机床热膨胀系数为11.7×10-6°C-1，温度变化范围为（20±1）℃，由式（14）计算得到utemp=0.827 3μm，结果表明温度对测量不确定度的影响较大。因此，在测量前，在对机床预热的同时须将球杆仪置于相同环境下，以减小球杆仪与机床的温差。

在正确使用球杆仪的条件下，其示值误差仍不可避免。根据QC20-W型号球杆仪的使用说明书，确定由其示值误差引起的测量不确定度uind≤0.100 0 μm。

表3 球杆仪测量系统显示的某加工中心ZX平面圆度误差各贡献因素的测量结果Table 3 Measurement results of each contributing factor to roundness error of ZX plane of a machining center displayed in the ballbar measurement system

表4 球杆仪测量系统显示的某加工中心ZX 平面圆度误差各贡献因素的测量不确定度Table 4 Measurement uncertainty of each contributing factor to roundness error of ZX plane of a machining center displayed in the ballbar measurement system单位：μm

通常情况下，由灰尘引起的测量不确定度udu=0.200 0 μm［17］。

在球杆仪校准过程中，电噪声和机械噪声是常见的。查阅文献［21］中的附录C可知，由噪声引起的测量不确定度极小，几乎可以忽略，保守估计由噪声引起的测量不确定度uno≤0.020 0 μm。

综上所述，基于测量结果合成的加工中心ZX平面圆度误差的标准不确定度为：

4.3 MCM对比验证

MCM 是已被广泛应用的测量不确定度计算方法［11］，本文利用MCM 来验证所提出方法的可行性。基于MCM的测量不确定度的计算步骤为：

1）建立测量过程模型；

2）根据已知信息确定输入量的分布类型以及均值和方差等特征值；

3）确定模拟次数M，若无特殊限制可取106；

4）根据各个输入量的分布类型，生成M组输入量随机数；

5）将各组输入量随机数代入输出函数，得到M个输出值，输出值的标准差即为标准不确定度。

利用MCM模拟计算得到：球杆仪中心偏移坐标为（23.1，56.8）μm，最佳拟合半径为100 013.0 μm。分别计算最佳拟合圆心相对原点的偏角α与最佳拟合圆心相对原点的偏距C。根据半径测量值rt的分布规律，设其服从高斯分布，产生106组随机数，计算某加工中心ZX平面的圆度误差。基于MCM的模拟圆度误差的分布情况如图5所示。由图5可得，模拟圆度误差的标准不确定度为1.160 0 μm。

图5 基于MCM 的某加工中心ZX 平面的模拟圆度误差的分布情况Fig.5 Distribution of simulated roundness error of ZX plane of a machining center based on MCM

上述模拟计算以球杆仪测量系统中的数据为依据，模拟结果与所提出方法的评定结果的相对偏差为2.5%，由此说明所提出方法的评定结果的可信度较高。需要强调的是，对于一定实验条件下得到的测量数据，不确定度为其固有属性，其理论值的大小不可改变且难以准确得出，进而无法确定2种评定结果与理论值的接近程度，因此所提出方法与MCM的优劣比较不以评定结果的数值大小来评判。但所提出方法的优势在于：规避了繁杂的输入量与输出量之间函数关系的求解过程，简化了机床圆度误差测量不确定度的评定过程。本方法适用于测量误差的来源因素较多且各因素的影响程度相同的情况。

在上述评定中，本文所提出方法的评定结果偏大的原因可能是球杆仪测量系统内设定的强相关因素之间的相关性系数偏大，但本文旨在利用实例来验证所提出评定方法的可行性，因此并未对相关性系数进行深入分析。

4.3 不确定度报告

本次实验利用球杆仪对加工中心ZX平面圆度误差进行测量。通过测量可得，运行圆轨迹的标称半径为100 013.0 μm，圆度误差的测量结果为17.450 0 μm，圆度误差的标准不确定度uc=1.190 0 μm，包含概率95%条件下的包含因子为2，则扩展不确定度u95=2.380 0 μm。则该加工中心ZX平面圆度误差的最终结果为19.830 0 μm。

5 结 论

针对机床圆度误差测量准确度的问题，从误差来源、贡献因素及不确定度评定方法三个方面综合考虑，实现了基于多源融合理论的机床圆度误差测量不确定度的评定。

1）鉴于机床圆度误差通常由多个因素造成，提出了多源融合误差测量不确定度评定方法。针对圆度误差与其贡献因素之间的函数关系难以求解的难题，引入黑箱理论，直接从误差源出发，先计算了圆度误差各贡献因素的不确定度，再通过合成得到总不确定度。

2）建立了基于球杆仪的机床圆度误差测量不确定度评定体系和评定模型。MCM验证结果表明，所提出方法的评定结果与MCM 模拟结果的一致性较高，验证了所提出方法的可行性。所提出方法规避了繁杂的输入量与输出量之间函数关系的求解过程，简化了不确定度评定过程。

3）通过研究发现，用精密仪器测量机床几何误差时，温度的影响远大于其他外界环境因素。在工程实践中，若对测量不确定度的要求不高，则可适当忽略其他因素的影响，以降低计算难度和提高工作效率。