圆柱形货物摆放公式计算法的改进与完善
贾春玉,朴惠淑
(1.广东培正学院 管理学院, 广东 广州 510830; 2.大连海事大学 交通运输工程学院,辽宁 大连 116026)
条块状货物装箱问题研究成果众多[1-2],但圆形货物装箱问题研究成果非常少,多数为圆形货物下料问题[3-4]。装箱与下料问题虽然互为反问题,有些方法可以互用,但还是有明显区别的,许多情况下不能直接互用。在生产实践中,经常遇到的同尺寸圆柱形货物装箱(或称下料)问题,传统方法是凭经验装箱或下料,优化程度低、成本高。为了解决这类问题,人们提出了多种解法。如动态规划算法[5-6]、递归解法[7-9]和启发式算法[10]等。这些方法虽然可解决这类问题,但通常需要建立较为复杂的数学模型、编制求解软件进行求解,不易掌握;有些方法求解时间过长,影响实际运用。圆柱形货物压缝式摆放通常比对齐摆放方式的优化程度高,且易于计算摆放数量,求解时间很短,但有时的优化程度不高。虽然有人为此提出了“三块法[6]”和“四块法[11-13]”等,但它们的具体解法主要还是动态规划算法、递归解法和启发式算法等。
公式计算法虽然略微繁琐,但与其他方法相比(如规划求解法),更容易理解,易于掌握,且运用Excel软件可快速求解,获得满意近似最优解。为此,有必要针对原有公式计算法进行研究,改进与完善公式计算法。
1 圆柱形货物摆放的方式
圆柱形货物摆放方式多种多样,常用的有5类。第一类是上下对齐式摆放(在下料排样中称为并排),简称对齐式(图1)。第二类是紧凑压缝式摆放(在下料排样中称为品排),简称紧凑式。它又可分为2种摆放方式。其中,横排紧凑压缝式摆放简称横排紧凑式(图2),即货箱长度L方向对应货物摆放高度方向,货箱宽度K方向为横向;竖排紧凑压缝式摆放简称竖排紧凑式(图3),即货箱宽度K方向对应货物摆放高度方向,货箱长度L方向为横向。第三类是紧凑式和对齐式相结合摆放。它又可分为下列2种摆放方式:一是在横排紧凑式基础上进行对齐摆放(图4);二是在竖排紧凑式基础上进行对齐摆放(图5)。第四类是横排和竖排相结合的摆放方式。它又可分为下列4种方式:一是横着将货箱分割成两部分,让两部分分别按紧凑式摆放;二是在横着分割货箱的基础上,紧凑式加对齐式摆放(横着分割货箱的摆放方式如图6所示);三是竖着将货箱分割成两部分,让两部分分别按紧凑式摆放;四是在竖着分割货箱的基础上,紧凑式加对齐式摆放。竖着分割货箱的摆放方式如图7所示。
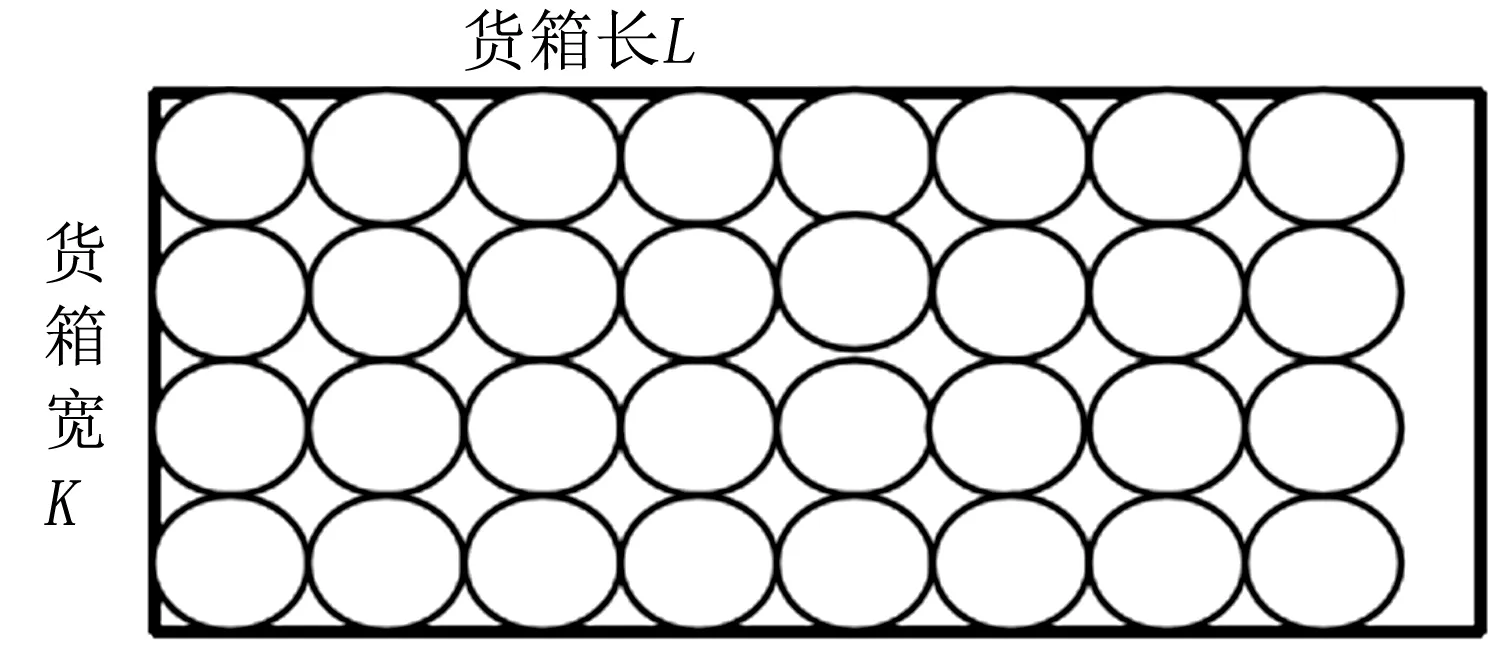
图1 上下对齐式摆放(对齐式)

图2 横排紧凑式
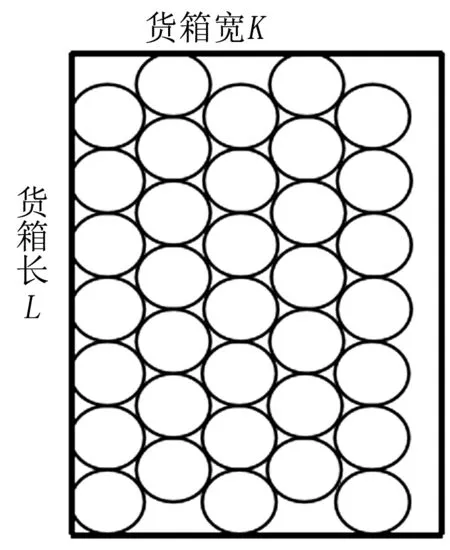
图 3 竖排紧凑式
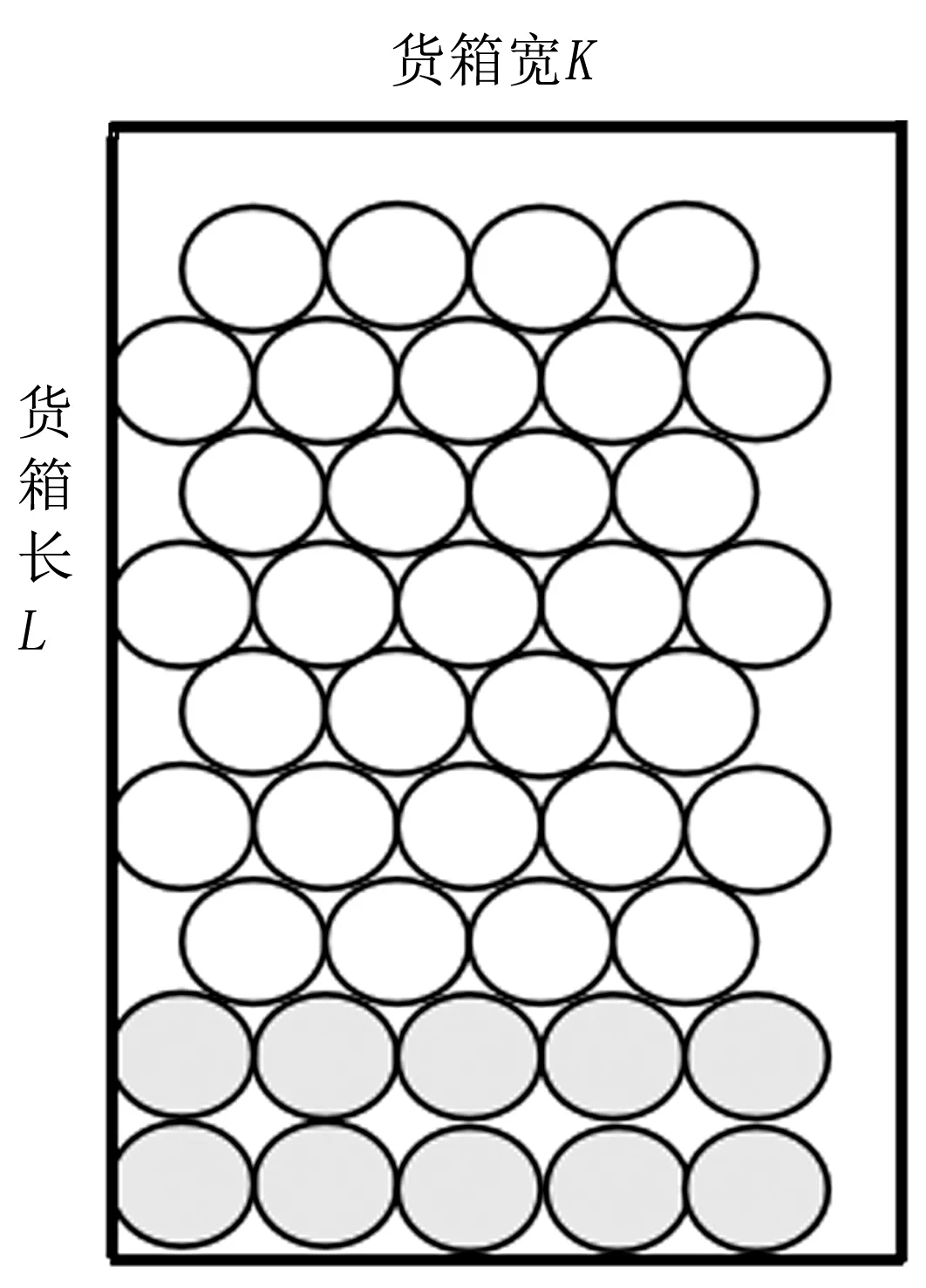
图4 横排紧凑式基础上的对齐摆放
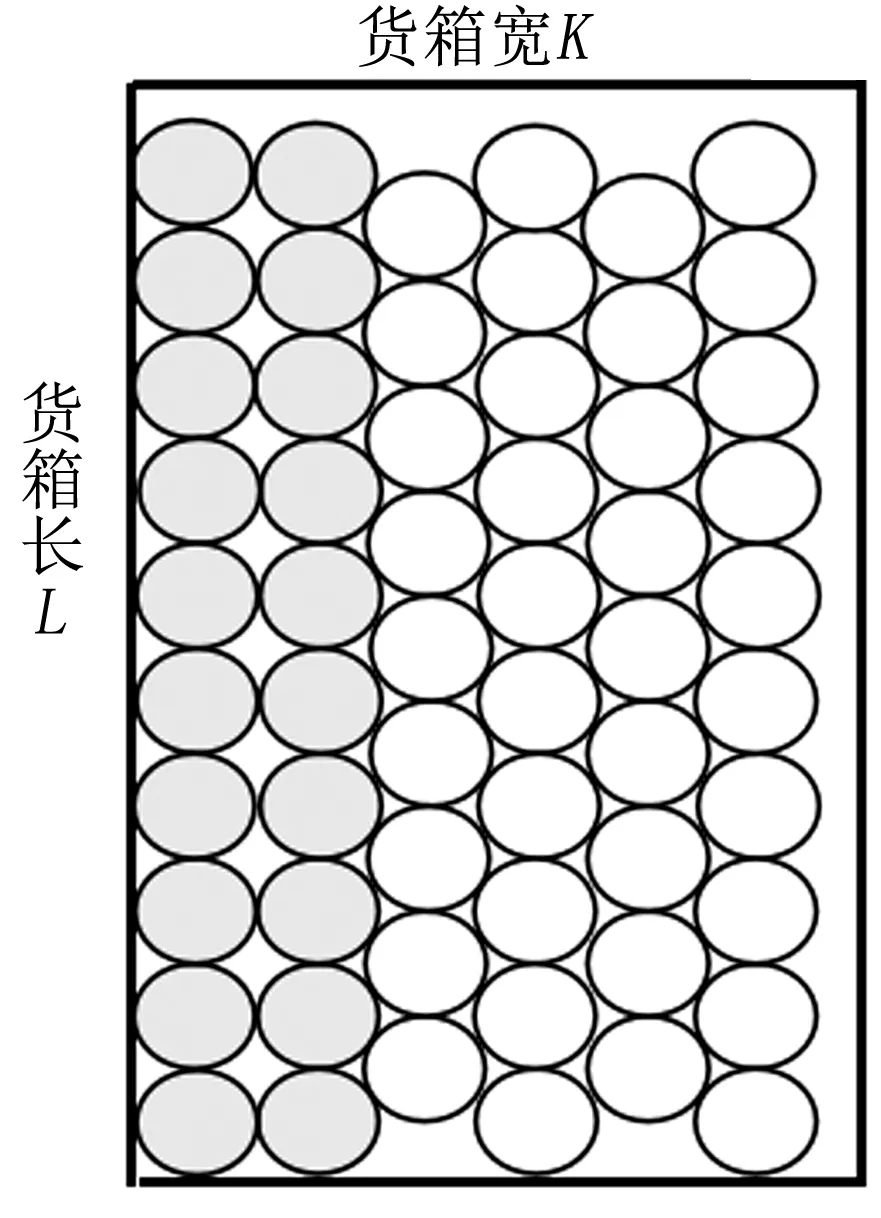
图5 竖排紧凑式基础上的对齐摆放
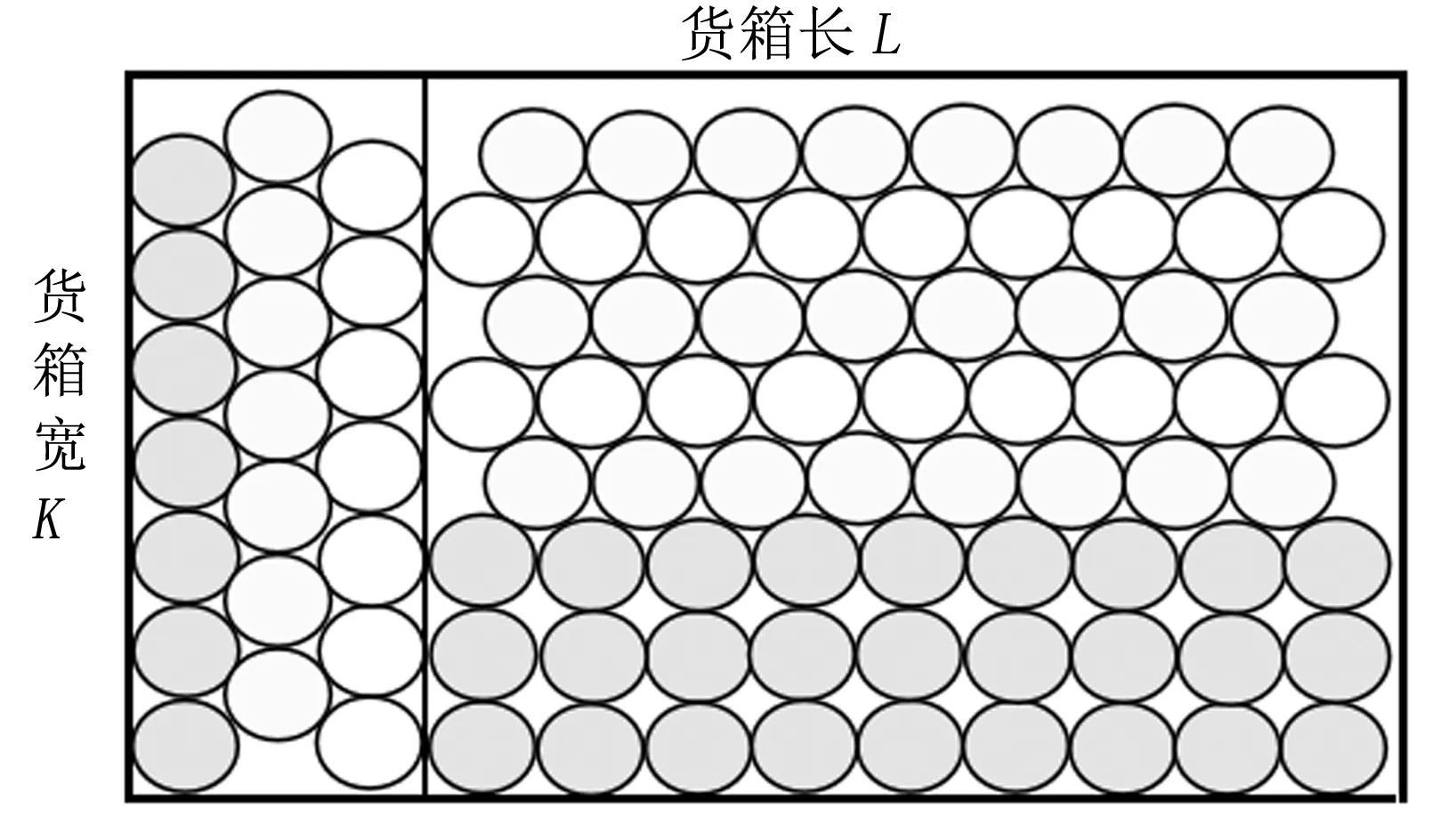
图6 横着分割货箱的摆放方式
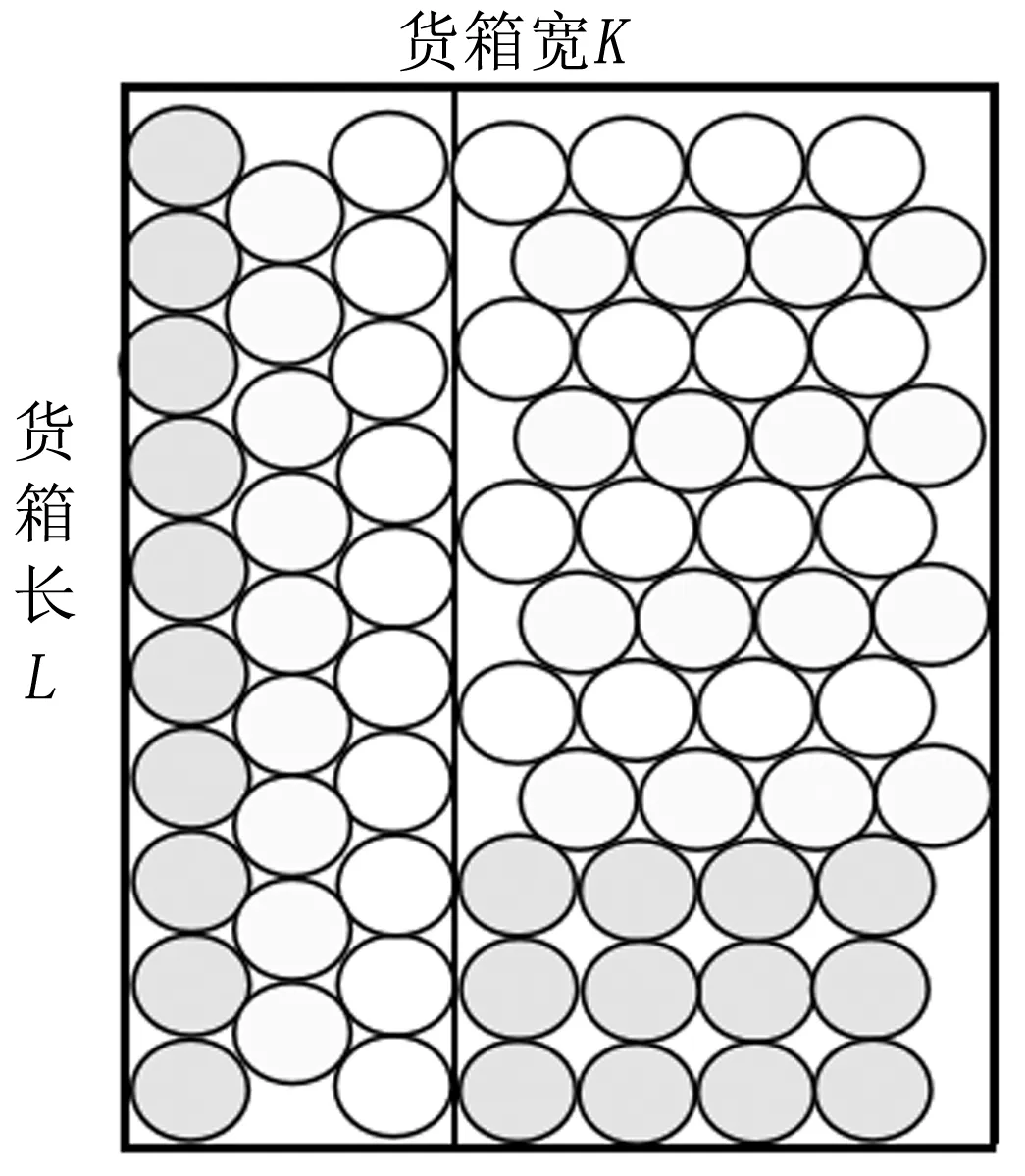
图7 竖着分割货箱的摆放方式
2 圆柱形货物摆放的计算公式
2.1 对齐式符号设定及摆放货物数量计算
设货箱长为L,宽为K,圆柱形货物半径为R,货物在L方向摆放数量为NL,在K方向上摆放数量为NK,可摆放货物总数为NQ,则
(1)
式中,符号[ ]1代表向下取整。
2.2 紧凑式符号设定及摆放货物数量计算
设H为紧凑式摆放货物的高度,Hn为n层货物摆放的高度,n为高度方向摆放货物总层数。
以货箱长L为摆放高度 (横排紧凑式摆放)时,摆放数量为NJL,对齐摆放层数为DNL,压缝摆放层数为YNL,剩余高度为SHL;以货箱K为摆放高度(竖排紧凑式摆放)时,摆放数量为NJK,对齐摆放层数为DNK,压缝摆放层数为YNK,剩余高度为SHK,则根据几何知识,有
紧凑式摆放的每层货物高度为:
H=30.5R
(2)
以紧凑式摆放货物时,每层货物节约的高度为:
G=2R-30.5R
(3)
以货箱长L为摆放高度时,高度方向摆放货物总层数为:
n≤ [(L-2R)/(30.5R)+1]1
(4)
摆放总高度为:
Hn=(n-1)×30.5R+2R
(5)
垛高方向(即货箱长L方向)剩余高度为:
SHL=L-[(n-1)×30.5R+2R]
(6)
对齐摆放层数为:
DNL=[n/2]1
(7)
式中,符号[ ]1代表向上取整。
压缝摆放层数为:
YNL=[n/2]1
(8)
以货箱长L为摆放高度时,横排紧凑式摆放数量的计算可分下列2种情况:
当K-[K/(2R)]1×2R
NJL=n×[K/(2R)]1-[n/2]1
(9)
当K-[K/(2R)]1×2R≥R时,
NJL=n×[K/(2R)]1
(10)
货物在L方向的摆放数量为:
NL=n×[K/(2R)]1-{[K/(2R)]1-[(K-R)/(2R)]1} ×[n/2]1
(11)
以货箱宽K为摆放高度时,计算公式与上述以货箱长L为摆放高度时类似,只需把L和K互换即可,即从横排紧凑式转换为竖排紧凑式。
圆柱形货物紧凑式摆放数量为:
NJ=max(NJL,NJK)
(12)
3 公式计算法的改进
3.1 第一类改进方法
第一类改进方法是剩余垛高空间增加摆放数量法,即分析剩余垛高是否可通过压缝式转换成对齐式而多摆货物。其判断条件为:K-[K/(2R)]1
对应于式(3)和式(6),剩余高度可把紧凑压缝式摆放层数转变为对齐式摆放的层数为:
SNL=[SHL/G]1
(13)
因为剩余高度小于H,即SNL
[SHL/G]1≤[30.5R/(2R-30.5R)]1=6
(14)
即在剩余空间内最多可把紧凑压缝式摆放转变为6层的对齐式摆放。紧凑式包括奇数层和偶数层。其中,奇数层每层摆放个数与对齐式相同;偶数层在K-[K/(2R)]1
当DNL=YNL即[n/2]1=[n/2]1时,最顶层为压缝式摆放(偶数层),摆放数量比对齐式摆放(奇数层)少1个。此时,由压缝式转变为对齐式摆放货物增加的层数为:
SDNL=[SNL/2]1
(15)
当DNL>YNL即[n/2]1>[n/2]1时,最顶层为对齐式摆放(单数层),由压缝式转变为对齐式摆放货物增加的层数为:
SDNL=[SNL/2]1
(16)
对于紧凑式摆放,当K-[K/(2R)]1×2R≥R时,式(12)成立;当K-[K/(2R)]1×2R
NJ=max(NJL+SDNL,NJK+SDNK)
(17)
式中:SDNK为竖排紧凑式下,由压缝式转变为对齐式摆放时增加的货物层数。
3.2 第二类改进方法
第二类改进方法是横切法,即按货箱长度方向横着分割货箱(分割线与货箱宽度边缘平行)。其分割方式有下列2种:一是以2R+H为长度划分割线,分割后对剩余部分L-(2R+H)采用压缝式摆放的公式计算法,计算横、竖2种摆放方式下总的摆放数量,择优作为优化结果;二是以2R+2H为长度划分割线,分割后对剩余部分L-(2R+2H)采用压缝式摆放的公式计算法,计算横、竖2种摆放方式下总的摆放数量,择优作为优化结果。
3.3 第三类改进方法
第三类改进方法是竖切法,即按货箱宽度方向竖着分割货箱(分割线与货箱长度边缘平行)。其分割方式有下列2种:一是以2R+H为长度划分割线,分割后对剩余部分K-(2R+H)采用压缝式摆放的公式计算法,计算横、竖2种摆放方式下总的摆放数量,择优作为优化结果;二是以2R+2H为长度划分割线,分割后对剩余部分K-(2R+2H)采用压缝式摆放的公式计算法,计算横、竖2种摆放方式下总的摆放数量,择优作为优化结果。
4 圆柱形货物装箱问题求解实例
4.1 实例1
货箱长(L)2 000 cm、宽(K)1 000 cm,货物为半径(R)71.5 cm的圆柱形,需求解货箱中最多能摆放货物的数量。
4.1.1 采用第一类改进方法求解
因为R=71.5 cm,所以2R=2×71.5=143(cm)。
NL=[L/(2R)]1=[2 000/143]1=13(个),
NK=[K/(2R)]1=[1 000/143]1=6(个),
NQ=[L/(2R)]1×[K/(2R)]1=13×6=78(个)。
H=30.5R=30.5×71.5≈123.84(cm),
G=2R-30.5R=143-123.84=19.16(cm),
n≤[[(L-2R)/(30.5R)]+1]1=[[(2 000-143)/123.84]+1]1=15(层),
Hn=(n-1)×30.5R+2R=(15-1)×123.84+143=1 876.78(cm),
SHL=L-[(n-1)×30.5R+2R]=2 000-1 876.78=123.21(cm),
DNL=[n/2]1=[15/2]1=8(层),
YNL=[n/2]1=[15/2]1=7(层)。
因为K-[K/(2R)]1×2R=1 000-[ 1 000/143]1×143=142>71.5,所以奇数层和偶数层摆放数量相等,有:
NJL=n×[K/(2R)]1=15×[1 000/143]1=15×6=90(个)。
因为奇数层和偶数层摆放数量相等,所以剩余高度无法通过压缝摆放将奇数层转变为对齐摆放层来增加摆放数量。
因此,SDNL=0。
把货箱长L与货箱宽K对调,即运用Excel计算时,把这2个数据对换,计算可得:
NJK=91 个,SDNK=0。
根据式(17),NJ=max(90+0,91+0)=91(个)
4.1.2 采用第二类改进方法求解
因篇幅所限,这里不再进行具体计算,而只给出第二类改进方法(横着分割货箱)的下列计算结果:横切长度为2R+H,即266.842 cm;切掉部分总尺寸为1 000×266.842 cm,可摆放12个;剩余部分总尺寸为1 000×1 733.158 cm,可摆放83个;最终摆放数量为两部分摆放数量之和,即95个。
4.1.3 采用第三类改进方法求解
因篇幅所限,这里不再进行具体计算,而只给出第三类改进方法(竖着分割货箱)的下列计算结果:竖切长度为2R+H,即266.842 cm;切掉部分总尺寸为2 000×266.842 cm,可摆放26个;剩余部分总尺寸为2 000×733.158 cm,可摆放71个;最终摆放数量为两部分摆放数量之和,即97个。
4.2 实例2
以文献[9]下料问题为例。原材料长L为600 mm,宽K为430 mm。下料货物为半径(R)15.5 mm的圆形截面毛坯。需求解原材料能下毛坯的最大数量。
分析可知,文献[9]下料问题没有最大下料排数限制,没有加工余量要求,与装箱问题一样。文献[9]解法可下282个毛坯。运用公式计算法按货箱长度优化,可摆放286个毛坯;竖切长度为2R+H,即26.86 mm,切下部分尺寸为600 mm×26.85 mm,可摆放37个,剩余部分尺寸为600 mm×372.15 mm,按货箱长度进行优化,可摆放254个,最终摆放数量为两部分摆放数量之和,为291个毛坯(竖着分割货箱时)。
显然,本文改进的公式计算法好于文献[9]递归解法。
5 几种方法的比较
随机试验50个样本,货物半径尺寸区间为8.5~71.5 cm,货箱二维尺寸区间为190~3 000 cm。分别用改进前压缝摆放方式、第一类改进方法、第二类改进方法(横切法)和第三类改进方法(竖切法)计算摆放数量。
改进前压缝摆放方式的优化程度较高,但当货箱边缘摆放后剩余尺寸较大时,优化程度不理想,在50个随机样本中,改进前压缝摆放方式有35个样本为摆放数量最多状态,占样本总数的70%;第一类改进方法有36个样本为摆放数量最多状态,占样本总数的72%;第二类改进方法中横切(以2R+H为长度划分割线)时有13个样本为摆放数量最多状态,占比26%;第三类改进方法中竖切(以2R+H为长度划分割线)时有14个样本为摆放数量最多状态,占比28%,竖切(以2R+2H为长度划分割线)时有23个样本为摆放数量最多状态,占比46%。3类改进方法合计比改进前摆放数量最多状态多出现15次,占比30%,可见,有30%的样本可提高优化程度。在这15次中, 第一类改进方法有1次且是与竖切(以2R+2H为长度划分割线)时共同出现的摆放数量最多状态,占比改进前摆放数量最多状态多出现次数的6.7%,共有4次比改进前摆放数量多,占能改进的比例为26.7%。第二类改进方法中横切(以2R+H为长度划分割线)时有1次摆放数量为最多状态,占比改进前摆放数量最多状态多出现次数的6.7%,共有2次比改进前摆放数量多,占能改进的比例为13.4%。第三类改进方法中竖切(以2R+H为长度划分割线)时有5次最多、占比改进前摆放数量最多状态多出现次数的33.3%,共有7次能改进,占能改进的比例为46.7%;竖切(以2R+2H为长度划分割线)时有9次最多,占比改进前摆放数量最多状态多出现次数的60%,共有13次能改进,占能改进的比例为86.7%。第三类改进方法摆放数量最多状态合计14次,占比改进前摆放数量最多状态多出现次数的93.3%,第三类改进方法能改进合计次数为15次,占能改进的比例为100%。可见,这3类改进方法都可以多摆放货物、提高优化程度,但效果不同,第三类改进方法的效果最好。
6 结 论
压缝摆放的公式计算法改进前虽然多数情况(约70%)的优化程度较理想,但优化程度仍有提升空间。随机试验显示,运用本文3类改进方法时30%可提高优化程度,第一类改进方法(即剩余垛高空间增加摆放数量法,能增加的摆放数量有限,最大值为3个;第二类改进方法(即横切法),约26.7%能提高原有压缝摆放方式的优化程度;第三类改进方法(即竖切法),约100%能提高原有压缝摆放方式的优化程度,是效果最好的改进方法。
压缝摆放问题解法较多,各有优缺点。非线性规划解法虽然数学模型简单、明了,但求解时可能会出现局部最优解,每次求解结果不一样,存在求解时时间过长的缺陷。其他启发式智能解法相对复杂、不易掌握、有时求解时间长、优化程度不够理想。公式计算法虽然计算工作量稍大,但容易理解,运用Excel软件编制计算公式后,只要输入原始数据即可快速得出三大类情况的各种优化方案,求解速度较快,优化程度较理想,便于实际运用。

