违约距离视角下上市公司信用风险度量及预测

王爱银，董万泉

(新疆财经大学 统计与数据科学学院，乌鲁木齐 830012)

对于企业来说，资金借贷等经济活动所面临的种种风险中，以信用风险为首，因此，如何正确评估信用风险已经成了当前社会最重要的问题之一。早在五六十年前就有学者对信用风险进行研究，他们通过构建模型和提出相应的评估方法做出了不少贡献，如今对信用风险的研究已经有了很多成果。从Black-Scholes创立了期权定价理论到后续的默顿模型，就仿佛打开了信用风险的大门。KMV公司于1993年提出了一种以期权定价公式为理论基础的KMV模型，结合上市公司财务数据和大盘指数，用资产和负债的关系来衡量上市公司的信用水平。然而，我国股票市场的发展不够完善，该模型随之暴露出一些问题，如模型前提假定的局限性和参数设定的不唯一性等。

我国股票市场做了大量的工作，对KMV模型参数设定作出了不同的修正。杨秀云等通过比较KMV、Credit Metrics、CPV和Credit Risk+这四大模型的优缺点和适用范围，将上市公司分为ST和非ST，实证表明，考虑公司财务数据的KMV模型度量结果更加可靠[1]。蒋彧、高瑜根据中国金融市场的特性，重新对KMV模型参数进行估计并修正，研究表明，修正后的KMV模型能有效识别上市公司信用状况，且具有一定的预测性[2]。张泽京等的研究，考虑到我国股票市场存在非流通股，并以每股净资产核算非流通股价格，还对股价波动建立了GARCH(1，1)模型，更加贴切我国股票市场[3]。李涛、张喜玲通过用企业限购股的计算来代替非流通股，用总利润的正负来区分违约和非违约组，最终验证出KMV模型对我国房地产行业具有一定的适用性[4]。王新翠等在修正股价波动上选取了刻画股价效果更好的SV模型，结果表明，SV模型在拟合数据上要优于GARCH模型[5]。邵翠丽基于牛顿迭代法下的高斯混合模型，对KMV模型中的变量d1和d2重新估计，得到的GKMV模型精准度要高于KMV模型[6]。曾玲玲等以上市公司为研究样本，建立BP-KMV模型来评估非上市公司信用风险，实证表明该模型适用性较好[7]。

上述文献主要是对KMV模型的参数和适用性做了改进，但并未对模型预测方面做出研究。Yusof使用KMV-Merton模型，通过预测三个不同评级公司的违约风险水平，对开发的安卓应用程序进行了测试，发现违约风险等级与相应公司的等级相当，证明模型具有的良好的预测性[8]。邹鑫等选取KMV模型和Logit模型对我国上市公司信用风险进行评估和预测，分析表明，Logit模型在做违约企业的信用风险预测上要优于KMV模型[9]。徐惠、胡颖利用KMV模型对科技型中小企业的信用风险进行测量，通过多元回归法找到了影响企业信用风险的关键性因素[10]。黄吉、蒋正祥将Logistic回归和KMV模型相结合，通过实证发现Logistic-KMV混合模型在预测准确率上要优于这两个分开的模型[11]。张勇基于CPV模型思路，把宏观因素与房地产信贷风险联系在一起，对风险定量进行分析，构建信贷风险模型，实证表明该模型具有一定的前瞻性[12]。

可见，邹鑫等是比较了KMV模型和Logit模型的预测效果，而徐惠和黄吉等是将二者相结合，侧重分析了违约的关键性因素和预测精度。KMV模型是以企业微观层面的财务数据为出发点，分析的是一种静态的非系统性风险，而CPV模型是将企业违约概率和宏观经济指标相联系，研究的是一种动态的系统性风险。因此，结合二者的优点，建立更加符合我国上市公司的KMV-Logistic模型来计算违约概率，并结合CPV模型利用宏观经济指数对上市公司的违约概率进行修正和预测，能增强模型的适用性。

一、模型建立

KMV模型是基于默顿理论和Black-Scholes期权定价公式发展而来用于度量上市公司信用风险的模型。该模型引入了一重要的因素——违约距离。当上市公司资产价值超过其发生违约时的负债值时，就存在违约距离。违约距离越大，表明公司在偿还负债后所能支配的资产越多，公司内部资金运营良好，发生违约的现象也就越低。

KMV模型假设上市公司资产价值服从正态分布，且分布保持平稳，主要通过上市公司的已知数据(如无风险收益率、违约点和股权价值及其波动率等参数)建立非线性方程组，并运用Matlab的fsolve迭代法编程，求解资产价值和资产波动率，最后代入式4得出违约距离。

由Black-Scholes期权定价公式得：

VE=VAN(d1)-De-rtN(d2)

(式1)

(式2)

其中，VE为股权价值，VA为资产价值，D为负债，DP为违约点，t为时间，r为无风险收益率，N(·)为标准正态分布的累积分布函数，σ为资产的年波动率。对式1两边同时取微分，化简后可求得：

(式3)

式1—式3组成了一个包含资产价值和其波动率的非线性方程组，可利用Matlab求解，进而根据公司违约点(DP)来计算违约距离(DD)，违约距离为超过违约点的资产预期价值与资产价值标准差的比值，公式如下：

(式4)

(一)上市公司的股权价值

由于我国股市的特殊性，上市公司的股权价值是由流通股股价和非流通股股价之和组成的。流通股股价由每股收盘价核算，而非流通股是由每股净资产核算。

(二)股权价值波动率

上市公司股票的对数收益率为：

(式5)

其中，pi为上市公司股票当日收盘价，pi-1为上市公司股票前一个交易日的收盘价。则该股票日收益波动率即标准差为：

(式6)

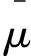
(式7)

从而可以推出:

(式8)

不过，由式8得出的波动率并未考虑股价的杠杆效应，即为无条件波动。不少研究表明，股价收益波动率并不服从标准正态分布，而是呈现尖峰厚尾的特点，且条件方差具有时变性，不同时期会呈现出不同的涨幅。

GARCH模型为广义自回归条件异方差模型，特别适用于分析和研究股价的波动性。由于GARCH对正负的影响相同，不能很好地描述收益率的非对称性。因此，采用可以刻画股价和收益波动率呈负相关的EGARCH模型，其均值方差如下：

yt=xγ+ρσ2+μ

(式9)

(式10)

(三)无风险收益率

无风险收益是指市场中没有一点风险而获得的收益率，在我国可用中国人民银行一年定期存款利率来代替。选取的研究时间跨度为2010—2019年，由于2016—2019年间的一年定期存款利率均为1.5%，即对2010—2019年间的一年定期存款利率按月加权平均作为KMV模型每年的无风险利率。

(四)违约点

违约点一般采用KMV公司长期实证得到的结果，认为公司违约点为短期负债与一半的长期负债之和时，公司发生违约的现象最为活跃。

二、实证分析

(一)数据处理

选取某A股上市公司近10年的股价每日收盘价，通过Eviews软件对其股价对数收益率进行描述性统计(见表1)。

表1 股价对数收益率描述性统计

从表1可知，峰度4.726135大于标准正态分布值3，说明收益率序列具有尖峰和厚尾的分布特征。接下来对序列进行ADF单位根检验(见表2)，确保其为平稳序列。

表2 ADF单位根检验

序列在1%的置信水平下拒绝原假设，因此序列不存在单位根，为平稳序列。再对残差平方进行相关性检验，表明序列存在自相关，所以有ARCH效应。因此，可建立GARCH模型，经过AIC和SIC准则，最终EGARCH(1，1)模型刻画股价波动效果最优。参数估计和检验结果如表3所示。

表3 日收益率EGARCH(1，1)的参数估计结果

因此，可建立EGARCH(1，1)模型：

(式11)

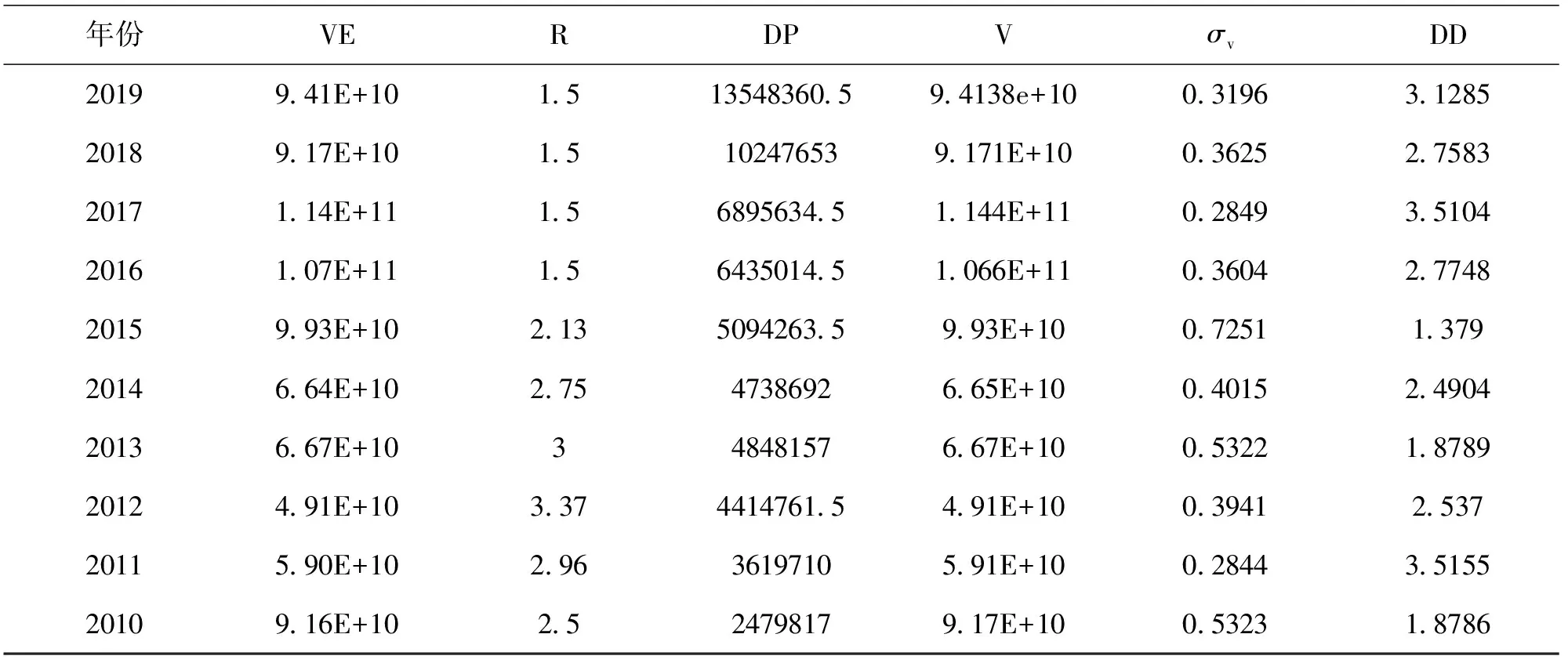
表4 2010—2019上市公司的违约距离

(二)基于Logistic回归的违约概率

Logistic Regression(逻辑回归)是一种研究被解释变量选取某个值的概率和解释变量之间的关系，目的是尽可能拟合决策边界，使样本尽可能分离，主要是用于解决二分类问题，非常符合企业信用风险(违约和不违约)问题。

为了全面考量企业财务指标对信用风险的影响，分别从企业运营、偿债、盈利和成长能力这4方面选取主营业务收入、净利润增长率、资产报酬率、流动速动比率、资产周转率等14个财务变量作为原始指标。对指标进行Mann-Whitney U检验，检验指标间的相关程度，通常认为，相关系数|r|>0.8时存在多重共线性。对于|r|≤0.8的指标，使用VIF法(VIF>10表示多重共线性)再次检验。

Mann-Whitney U和VIF法检验结果显示，一共剔除主营业务收入、净资产收益率、现金比率、速动比率和现金流量比等8个指标来尽可能减弱或消除各指标之间多重共线性问题。剩余净利润增长率、总资产增长率、资产报酬率、资产负债率、流动比率和资产周转率这6个主要指标(见表5)。先加入违约距离这一重要的影响因子，再利用因子分析和Logistic回归模型来解释各指标变量对违约率的显著性佑肔ogistic回归计算出违约概率。2010—2019年这7个财务指标历年的数据如表6所示,KMO和巴利特检验结果如表7所示。

表5 参数含义

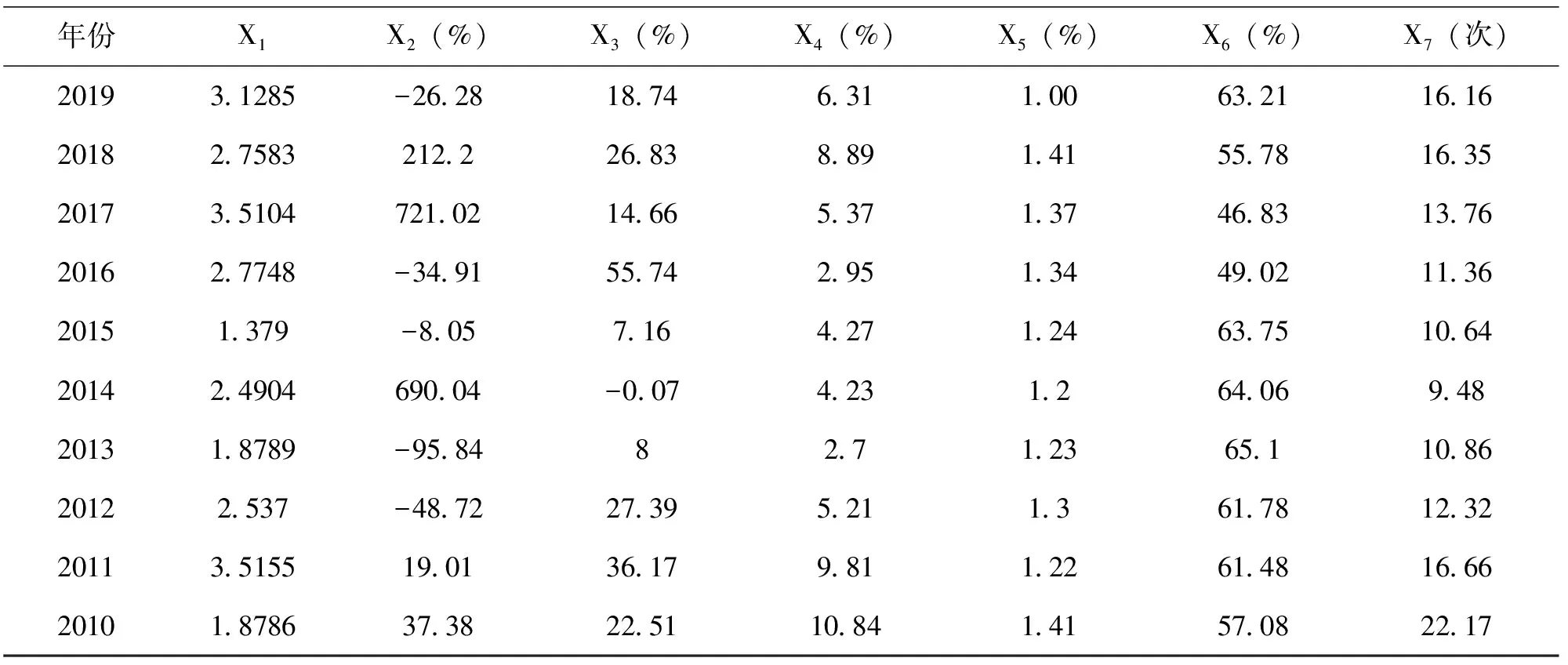
表6 上市公司的主要财务指标

表7 KMO 和巴特利特检验

从表7的结果可以看到，KMO统计值为0.606，Bartlett检验值为40.304，并且卡方显著性水平为0.07(小于0.1)，卡方值为44.766较大，从而拒绝原假设，各指标相关性较高，适合因子分析。

提取方法：主成分分析法。

由表8结果可以观察到，第3个主成分的累积贡献率已经达到了81.848%，说明这3个主成分里的信息量涵盖了其余变量的大部分信息。也就是说，这3个主成分极具代表性，它们与变量的相关程度极高，具有很强的解释能力。而碎石图(见图1)中前3个主成分的降速和坡度，也可以得出相同的结论。

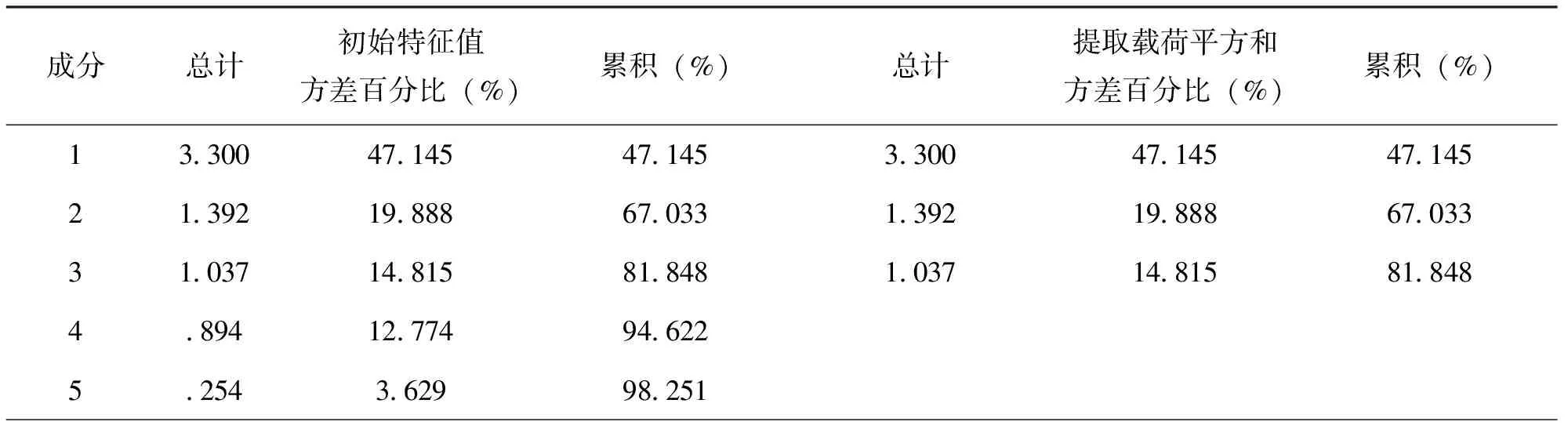
表8 总方差解释

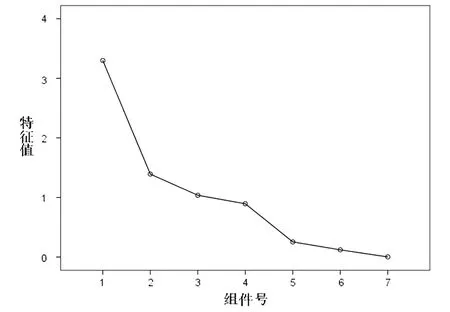
图1 碎石图

提取方法：运用主成分分析法提取了 3 个成分。

表9为3个公因子(主成分)矩阵，它代表着每个公因子包含了百分之多少的其余指标，即负荷值，是一种线性组合的关系，根据表9我们能准确地写出这3个公因子的代数表达式。

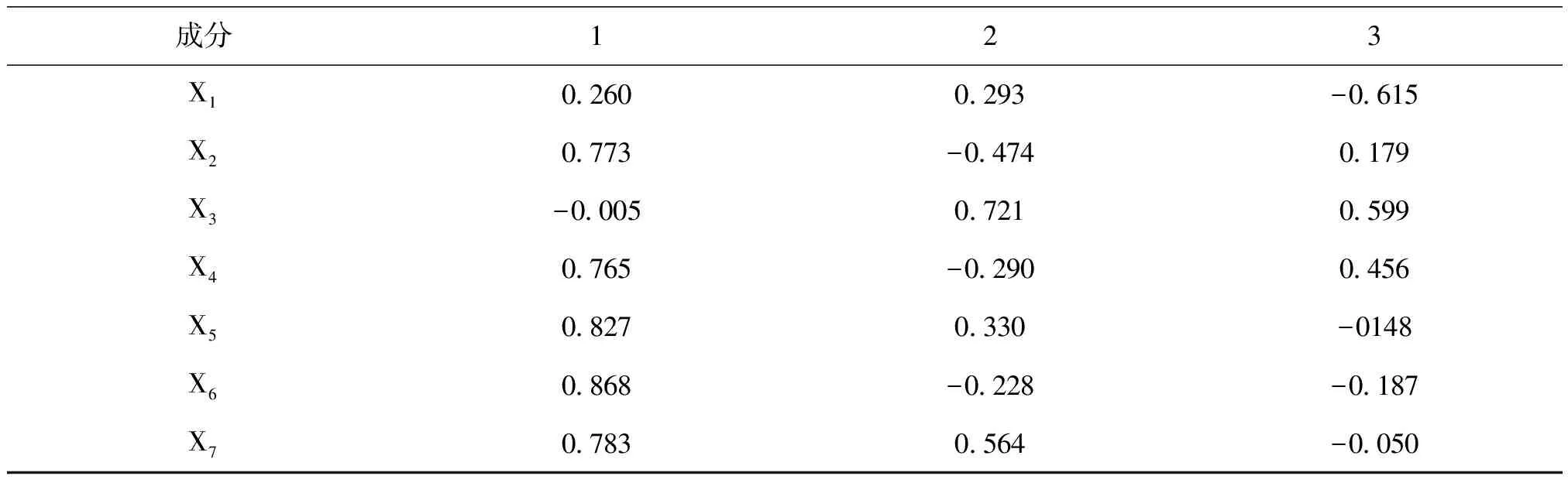
表9 成分矩阵

F1=0.226X1+0.773X2-0.005X3+0.765X4+0.827X5+0.868X6+0.783X7

(式12)

F2=0.293X1-0.474X2+0.721X3-0.290X4+0.330X5-0.228X6+0.564X7

(式13)

F3=-0.615X1+0.179X2+0.599X3+0.456X4-0.148X5-0.187X6-0.050X7

(式14)

同时，建立因子分析模型：

F=0.58F1+0.24F2+0.18F3

(式15)

可见，第一个公因子对因子分析模型的影响较为显著，起到了决定性的作用。将这个因子分析模型导入Logistic回归模型，其表达成为：

(式16)

所以，企业2010—2019年的违约概率PD=[35.9%，30.6%，34.7%，39.5%，36.9%，35.1%，21.1%，16.7%，12.4%，16.2%]

通过对企业2010—2019年财务指标的分析得出，2010—2014年的违约概率逐渐升高至35%，2014年后违约波动不明显，趋于一个稳定的状态，这可能与企业近年来迈向国际舞台的战略息息相关。

(三)利用CPV理论的宏观因素对违约概率进行修正

Credit Portfolio View模型(简称CPV模型)是Credit Metrics模型的衍生，其中的宏观经济因素对违约概率起决定性作用。比如，GDP增长率、储蓄率、汇率、固定资产投资和企业景气指数等宏观经济变量，不再是其他模型所用的股票波动率、资产价值等因素，该模型注重一国经济状况，倾向于市场中的系统性风险。CPV模型通过Logit函数把违约概率限制在0—1之间，表达式为：

(式17)

其中，Pt为企业在t时期内的违约概率，Yt为在t时期一个国家的宏观经济指数，表达式为：

Yt=β0t+β1tX1t+β2tX2t+…βntXnt+εt

(式18)

其中，ε～N(0，σ)将式16与式17合并化简，得到违约概率Pt：

(式19)

选取8个与企业相关的宏观经济指标：β1为国内生产总值增长速度、β2为财政支出增长率、β3为总储蓄率、β4为失业率、β5为城镇固定资产投资、β6为100美元兑人民币汇率、β7为企业景气指数、β8为长期利率。

在多元回归方法中选取了拟合效果更好的逐步向后回归法，为了保证单位为同一级别，进行数据处理，处理后数据显示均为平稳(见表10)。再将所有自变量引入回归方程，通过比较变量t值和F统计量以及AIC准则，其过程中同时引入和剔除自变量，在每一步消除显著性最小的自变量，消除了多重共线性的影响，保证了模型变量的最优。

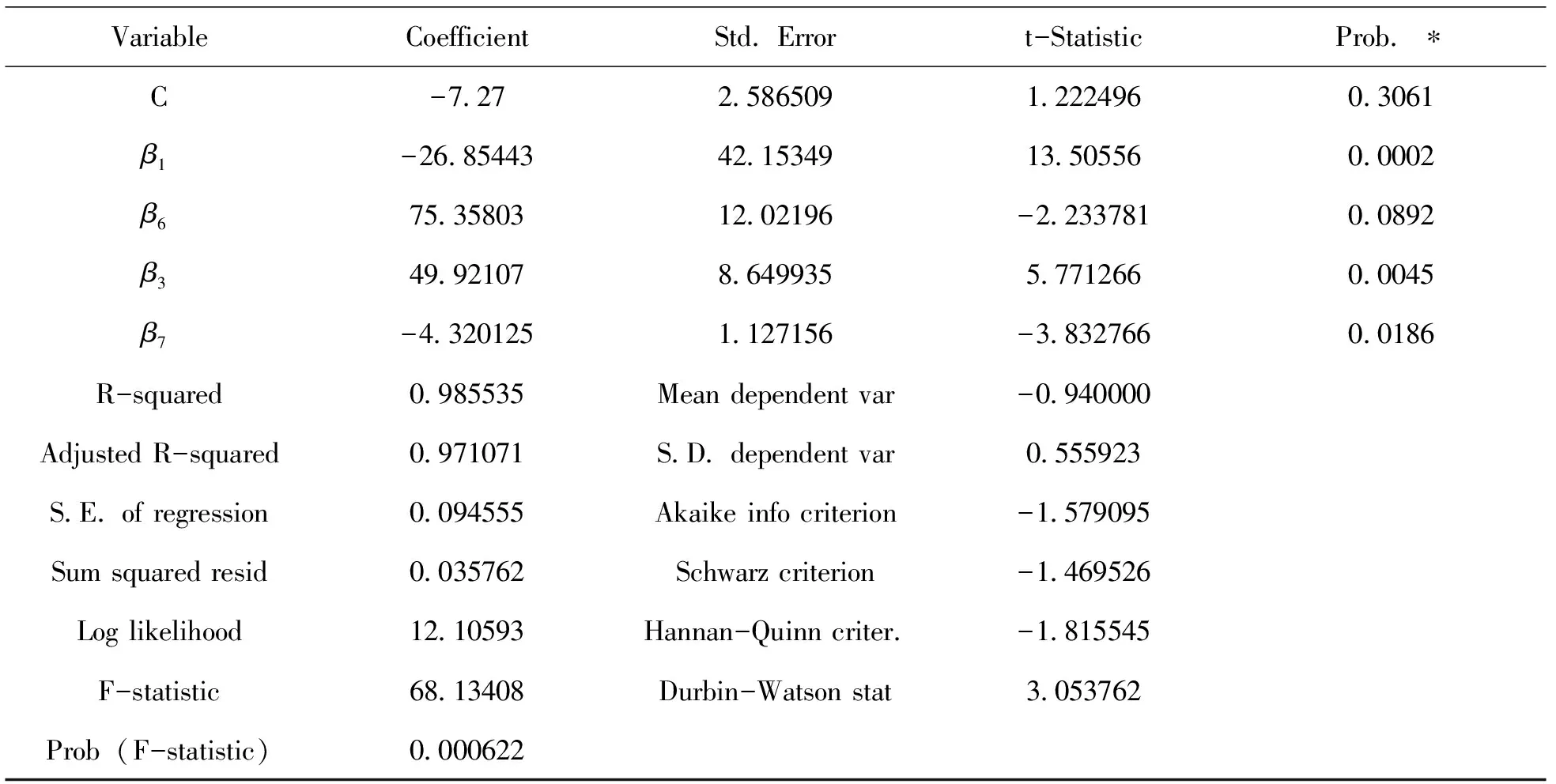
表10 逐步回归检验结果

在剔除财政支出、失业率、城镇固定资产投资和长期利率这些不显著的指标后，拟合优度为98.55%，调整后为97.11%，模型拟合效果较好。回归标准差为0.094，说明各变量的波动较小。DW值为3.054，大于5%显著水平下的du=1.70，说明不存在自相关。F统计量为68.13，也很显著，模型整体的解释能力较强。

Y实际值和拟合值的对比及其其残差走势如图2所示。

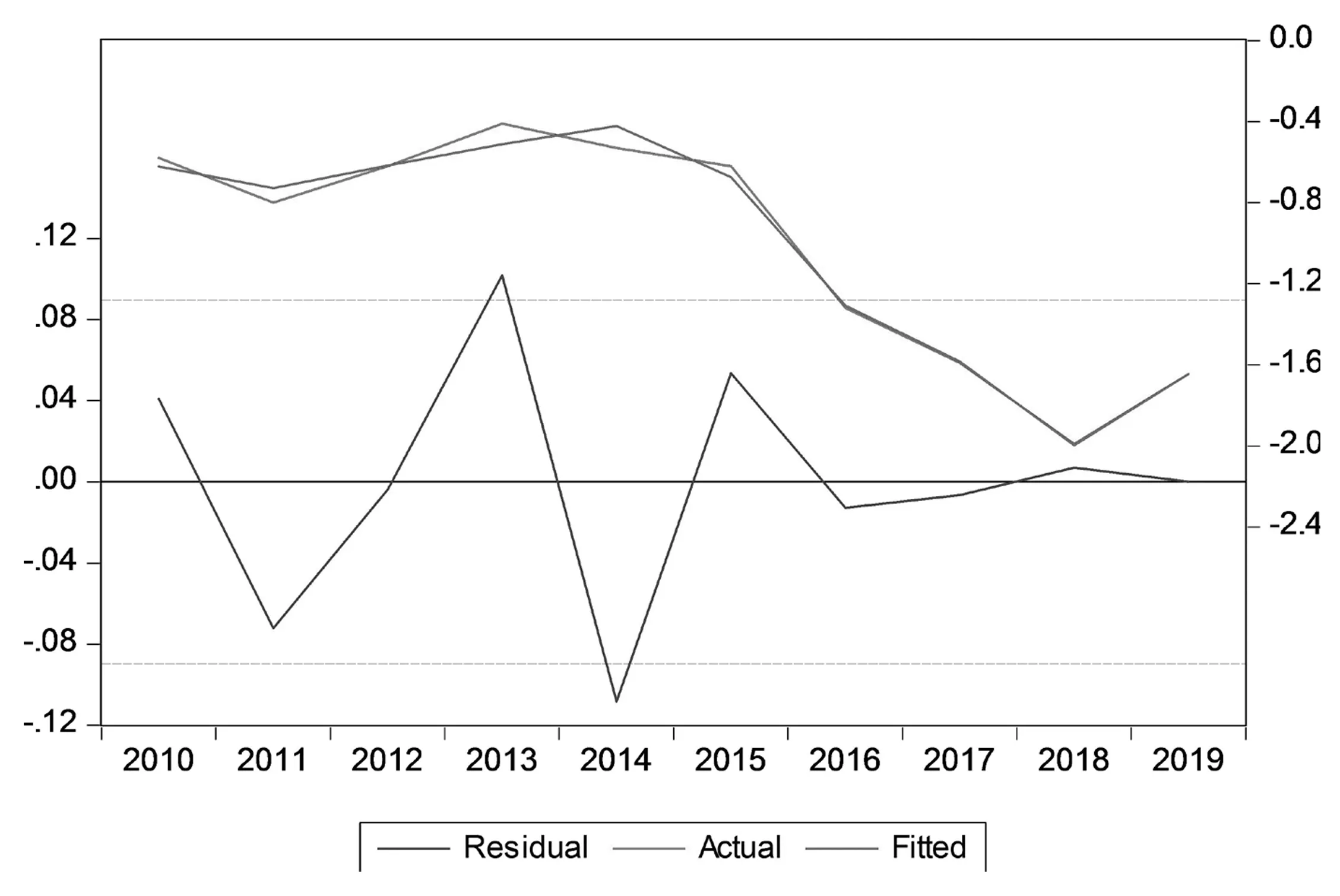
图2 宏观经济指数的实际值和拟合值对比及其残差分布情况

从图2可以看出，Y的实际值和拟合值曲线基本重合，拟合较好，进一步说明模型的有效性。因此，建立的上市公司的宏观经济回归模型为：

Y=-7.27-26.85β1+75.36β6+49.92β3-4.32β7

(式20)

由此可以看出，企业的违约概率与宏观经济指标息息相关，由式18得出Pt和Yt呈同向变动，且回归方程中储蓄率β3和Y值也呈同向变动。

1.指标因素分析

GDP增速与企业违约概率呈反向变动关系。当GDP增速下降时，表示经济不景气，经济活动低迷，一些地方债务一旦无力偿还，企业违约概率就会增高；反之，GDP增速上升，总体经济状况较好，经济高速发展，企业的违约概率自然降低。

汇率与企业违约概率呈正向变动关系。当美元兑人民币汇率下降时，人民币升值，若企业原材料依赖于进口，会降低成本使净利润增加，而且企业以外币核算的货币资金和负债都会产生相应的增值，从而导致违约概率降低；反之，汇率上升，人民币贬值，进口的生产成本增加，资金周转不足，同时以外币核算的借款会为企业带来更多的负债，从而导致高违约率现象。

储蓄率与企业违约概率呈正向变动关系。当储蓄率下降，银行放贷减少，利率有所升高，有利于存款，企业投资减小且伴随着风险降低，进而导致企业违约概率下降。

企业景气指数与企业违约概率呈反向变动关系。当企业景气指数高时，经济运行向好的方向发展，说明企业内部运营良好，资金周转流畅，违约现象较少，违约概率自然降低；反之，企业可能运转不良，资金周转不足，违约概率升高。

将2010—2019年的GDP、储蓄率、汇率、企业景气指数代入回归方程中，得到修正后的Y值，再将Y值代入式18中，得到修正后的企业违约概率。详情如图3所示。

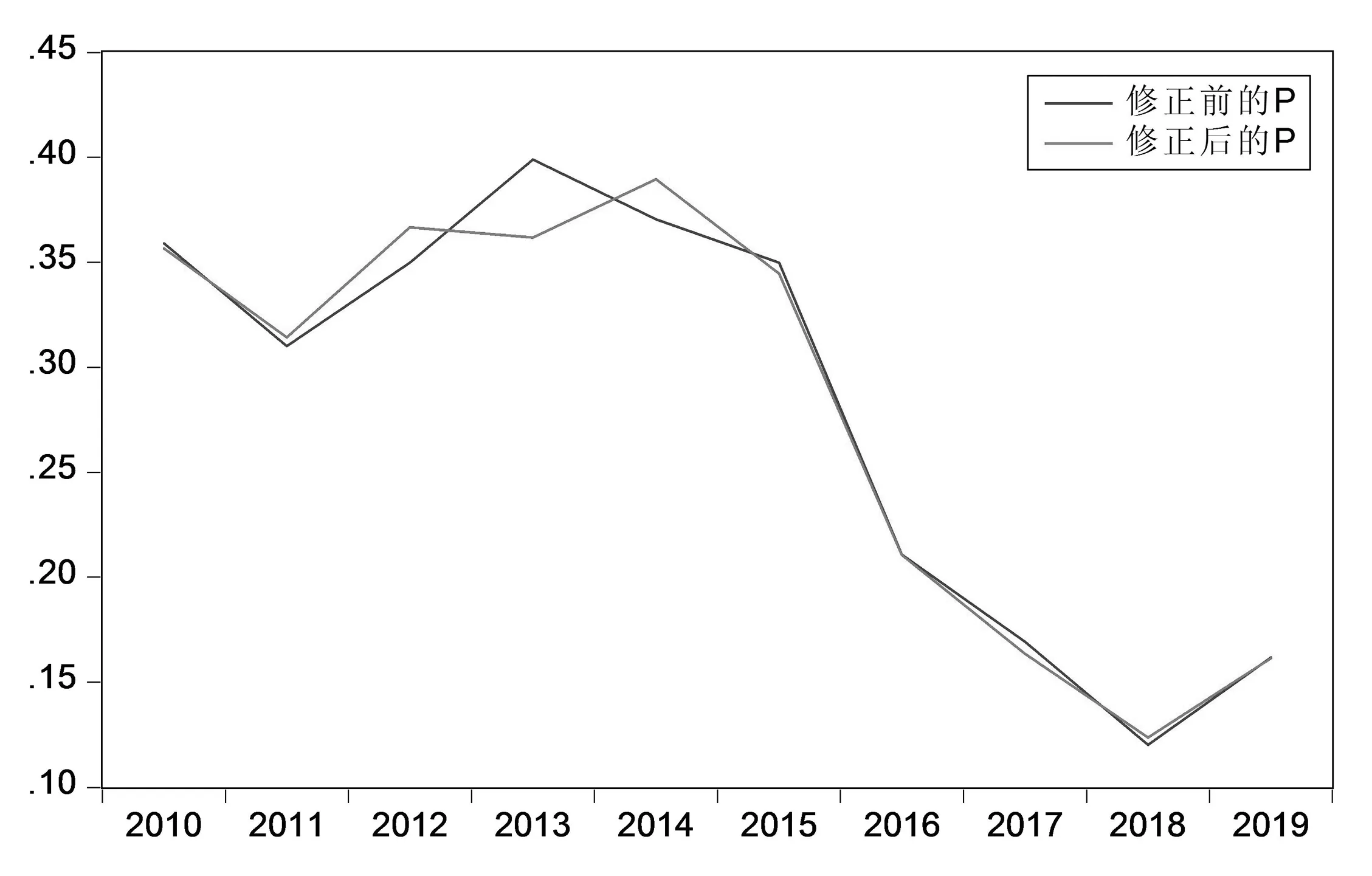
图3 违约概率修正前后对比图

2.模型预测

选取2020全年GDP、储蓄率、美元兑人民币汇率和企业景气指数这4大宏观经济指标。考虑到我国2020年的GDP和储蓄率还未公布，因此根据近10年的数据对2020年GDP和储蓄率建立AR(1)模型进行预测：

GDPt=0.68GDPt-1+0.02St=St-1-0.082

(式21)

将2019年的GDP增长率6.11%和储蓄率44.569%代入回归方程，得到2020年的GDP增长率和储蓄率预测值分别为6.40% 和43.79%，储蓄率总体还是呈下降的趋势，而GDP或许会稳中有升。然后把以上4个指标代入回归方程式20中，Y值得-2.953，再将Y代入式19中，得到上市公司2020年违约概率的预测值为4.955%。说明这与公司长期聚焦零售业密切相关，并且违约概率拟合图也与实际情况保持一致。

三、结论与建议

(一)结论

以某上市公司为例，选取2010—2019年的财务数据，通过引入违约距离建立KMV-Logistic模型，计算企业违约概率。在用CPV宏观理论对违约概率进行修正时，得出GDP增长率、储蓄率、汇率和企业景气指数这4个宏观指标对上市公司影响较大的结论。实证表明，修正后的模型适应性较好。

(二)建议

政府应该加强对上市公司的监管，坚决杜绝上市公司财务报表作假行为。企业应时刻关注宏观政策，了解国内外前沿信息，尤其是进出口贸易、国民经济和金融等方面的信息。企业内部应该成立信用管理部门，定期评估企业各部门的信用状况，认真核对每一笔业务，确保将可能发生的信用问题降低到最小，从而有效防范企业的信用违约风险。

在当今的大数据时代，企业的技术部门应合理应用信用风险度量模型，对自身违约状况进行及时的预警与防范。在企业扩大规模、提高业绩的同时，不仅要注重企业文化发展(如开展活动培养全体员工信用意识、增强自身素质和企业荣誉感)，而且还应建立与消费者、供应商之间的联系，消除信息不对称现象，使损失最小化，从而降低企业的违约概率。