计及直流系统影响的交直流受端电网静态电压稳定分析

李晖，盖振宇，蔡东阳，陈刚，江出阳，周保荣，姚文峰

(1. 国网经济技术研究院有限公司，北京102209；2. 直流输电技术国家重点实验室(南方电网科学研究院)，广州510663)

0 引言

高电压大容量直流输电是解决我国能源与负荷高度逆向分布的重要技术手段，随着北电南输和西电东送战略的实施，华东、广东等地区逐渐形成了直流多馈入的电网结构[1]。目前已投运的直流工程以基于电网换相换流器的高压直流(line commutated converter high voltage direct current，LCC-HVDC)为主[2 - 3]，LCC-HVDC为交流系统提供电力的同时消耗大量无功功率，其配置的以电容为主的无功补偿装置受电压水平影响较大，导致的无功不平衡加剧了电网的电压稳定风险[4]，直流系统灵活的控制策略给电压稳定性分析工作带来更多挑战，因此，准确把握交直流系统之间电压相互作用的机理和特性，对保证直流多馈入受端电网的良好运行有重要的意义。

电压稳定的分析方法主要包含动态分析法和静态分析法[5 - 8]。其中静态分析法具有计算量小、可以给出电压稳定性指标及其对状态变量、控制变量的灵敏度信息等优点，得以广泛应用。静态电压稳定分析常用的指标根据不同分析方法可分为状态指标[9 - 11]和裕度指标[12 - 14]。状态指标以临界点的某种特征作为判据，文献[10]提出了一种基于电压灵敏度的受端电力系统支撑强度评价指标对母线静态电压稳定进行判别；文献[11]基于等值耦合导纳的多端直流系统单端口等值模型提出等效节点功率灵敏因子，用于评估多直流馈入系统临界电压稳定。裕度指标用于衡量电网当前运行点到临界电压稳定点的距离，文献[13]论述了连续潮流法在计算电压稳定裕度时线性较好，具有灵活性和高鲁棒性的特点；文献[14]提出了一种基于负荷裕度随机特性的方法来计算系统电压失稳的概率。

连续潮流法是求取裕度指标的典型静态电压分析方法[15]。连续潮流法要求电网以某种过渡方式逐步逼近电压稳定临界点，求取潮流解路径，计算过程中能提供丰富的中间信息。为了有效求取直流馈入电网的静态电压稳定结果，需对直流系统的动态电压特性进行准确建模，目前已有大量研究[16 - 20]。文献[17]提出了换流器控制方式转换策略并应用于静态电压稳定分析；文献[18]给出换流变分接头调整策略，提出改进交替迭代法以计算交直流系统连续潮流；文献[19]基于直流系统控制方式与受端电网电压稳定性的关系，优化实际高压直流工程的运行方式。包含新型柔性直流的交直流系统静态电压稳定性分析也有一定的研究成果，文献[20]根据柔性直流系统控制方式和交直流耦合特性，基于交直流接口给定量进行交替迭代连续潮流计算；文献[21]通过求取含柔直系统中的功率参数关于节点电压的泰勒级数，进一步获取电压稳定临界点。在上述的研究中，对过渡方式的处理通常只考虑发电机和负荷的增长，缺乏对直流系统过渡方式的考虑，或者仅对直流系统某几个运行点进行离散分析，直流系统的控制模式则根据交流系统的状态被动调节。

本文基于连续潮流法提出一种包含直流过渡方式的静态电压稳定分析方法，引入直流功率参与因子修正连续潮流方程，表征在过渡方式中直流系统的参与作用，并充分考虑控制模式切换以及无功装置投切等动态过程，通过灵活配置交直流系统的过渡方式，可满足直流参与负荷功率增量平衡场景的分析需求，弥补现有研究成果和软件功能的缺失，对直流受端电网的运行与控制具有指导意义。最后，通过对南方电网某直流受端电网进行静态电压稳定分析，证明了本方法的有效性。

1 直流模型及其控制模式

1.1 直流系统数学模型

以6脉波LCC-HVDC系统为例，其数学模型[22]可用式(1)—(3)表示。其中，换流器的直流理想空载电压为：

(1)

换流器各项直流参数之间的关系可表示为：

(2)

整流侧与逆变侧的直流电压关系可表示为：

UdR=UdI+IdRd

(3)

式中：Ud0为直流理想空载电压；kT为换流变压器变比；Us为换流器交流母线电压；Ud、Id为直流电压、电流；θ为触发角α或熄弧角γ；RX为换相阻抗；φ为换流器功率因数角；Pd、Qd为直流功率和换流器所消耗的无功功率；下标R表示整流侧，I表示逆变侧。

1.2 直流系统控制模式

直流系统的控制主要可通过调节换流器控制角和换流变压器分接头两种方式实现。两种调节方式的速度相差数个数量级，换流器控制角调节速度非常快 (1～10 ms)，可实现电网扰动瞬间直流系统快速响应；换流变压器分接头调节速度则慢得多(5～6 s)，其作用是维持直流电压和控制角在合理的范围之内。两种方式联合控制，保持直流系统各项运行参数在合理范围内。

直流换流器一般包含4种控制模式：定功率(constant power，CP)控制，定电流(constant current，CC)控制，定电压(constant voltage，CV)控制以及定控制角(constant angle，CA)控制。通常整流侧换流器采用定功率控制或定电流控制模式，逆变侧换流器采用定电压或定控制角(熄弧角)控制模式。各控制模式的表达式可用式(4)表示。

(4)

式中下标包含s的量代表控制定值。

在正常的控制方式下，直流两侧根据不同组合可分为4种控制模式，包括定功率-定电压控制(CP-CV)，定功率-定熄弧角控制(CP-CA)，定电流-定电压控制(CC-CV)以及定电流-定熄弧角(CC-CA)控制。

换流变压器分接头具备一定范围的调节能力，调节模式可分为角度控制和电压控制。当换流器采用CC/CV模式时，换流变分接头采用角度控制，维持控制角在合理的范围之内；当换流器采用CA模式时，换流变分接头采用电压控制，维持直流电压在合理的范围之内。

1.3 换流器控制模式切换

直流系统的正常运行需满足以下边界条件。

1)整流侧触发角α和逆变侧熄弧角γ分别不小于最小触发角αmin和最小熄弧角γmin；

2)换流变压器的变比kT不超过其上下限kTmax,kTmin；

3)直流电流Id不大于直流线路最大电流Idmax。

在直流受端电网静态电压稳定分析场景中，随着过渡方式的恶化，换流站交流母线的电压将发生变化，直流系统必须改变其运行参数才能满足所传输的功率和运行电压的要求。考虑到换流变压器分接头调节的作用是优先维持直流电压和控制角稳定，因此对直流参数的调整策略是：首先调整两侧换流变压器变比直至限值，再调整整流侧触发角和逆变侧熄弧角直至限值。随着直流系统运行点的改变，一旦上述任一边界条件不能满足，便立即将其限定在相应的边界上，转换成另一种控制模式，下面进行具体分析。

采用CP或CC控制模式时，当换流器交流母线电压下降或直流传输功率需求上升时，首先调节换流变压器变比直至限值，进一步调节触发角，当直流电流达到限制而功率仍无法满足需求时，切换为CC控制模式(Id=Idmax)；

采用CV控制模式时，当换流器交流母线电压下降时，首先调节换流变压器变比直至限值，进一步调节熄弧角，当熄弧角达到限制而直流电压仍无法满足需求时，切换为CA控制模式(γ=γmin)；

采用CA控制模式时，当换流器交流母线电压下降时，调节换流变压器变比直至限值。

静态电压稳定分析中，直流送端靠近电源侧，换流器交流母线电压受直流受端负荷增长影响较小，一般不存在大幅上调直流电压的需求，因此暂不考虑整流侧切换为CA控制模式(α=αmin)的情况。此外，当直流控制参数达到限制后，不考虑后续过渡方式参数回到限值以内的可能性。过渡方式中直流换流器控制模式切换策略如图1所示。

图1 换流器控制模式切换策略Fig.1 Switching strategy of the converter control mode

2 直流模型潮流求解算法

对求解交流潮流的牛顿拉夫逊算法进行相应改进，可实现交直流网络潮流统一迭代求解[23]。计及直流换流器交流侧功率，功率平衡方程可写为

(5)

式中：ΔPi、 ΔQi为节点i的功率不平衡量；Psi、Qsi为节点i的有功功率、无功功率给定量；Pi、Qi为节点i的节点有功功率、无功功率，根据网络节点电压和导纳矩阵计算而得；Pdi、Qdi为节点i的直流系统注入有功功率、无功功率，对整流侧Pdi取负号，逆变侧则取正号。

在每一轮迭代求解中，包括换流器交流侧母线在内的所有交流节点电压给出，相当于式(1)中的直流理想空载电压已知。根据式(2)、(3)可列出直流系统求解方程如式(6)所示。

(6)

式中UdR0、UdI0分别为直流整流侧流理想空载电压和直流逆变侧流理想空载电压，其值由交流迭代结果确定，RXR、RXI、Rd为固定参数，方程中待求的直流变量有UdR、UdI、Id、 cosα和cosγ。根据直流两侧的控制模式，从式(4)中再选取2个方程即可联立求解上述直流变量。进一步根据式(2)求解直流系统注入有功、无功功率。

牛顿拉夫逊法中的功率平衡修正方程可写为：

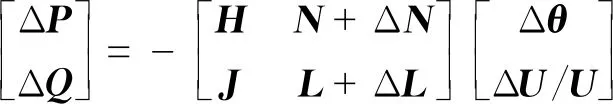
(7)

式中：H、N、J、L为交流网络的雅克比矩阵元素，ΔN、 ΔL为直流系统附加雅克比矩阵元素，Δθ为母线相位偏差量，ΔU为电压幅值偏差量。直流系统功率仅与交流侧母线的电压幅值有关，与相位无关，因此H、J无需修正。附加雅克比矩阵元素计算公式为：

(8)

式中：ΔNij、 ΔLij为节点i对节点j的附加雅克比矩阵元素；Uj为节点j的电压幅值。

由式(8)可知，ΔN、 ΔL实质是直流功率对交流母线电压的偏导数。对每个两端直流，仅需求取直流两侧有功功率、无功功率对两侧换流器交流侧母线电压的偏导数，因此ΔN、 ΔL是一个稀疏矩阵。根据换流器不同控制模式的表达式，可推导ΔN、 ΔL的计算公式[23]，当控制模式发生切换时，相应地修改雅克比矩阵元素。其余步骤与纯交流潮流迭代求解一致，本文不再赘述。

3 考虑直流过渡方式的连续潮流计算

3.1 计算模型和算法

静态电压稳定极限常采用的扩展潮流方程可表示为以下简化形式。

f(x)+λb=0

(9)

式中：f(x)为常规潮流方程；x为系统的状态变量，即待求节点电压幅值和相角；λ为负荷增长参数；b为系统中各节点的增长方式。

λb模拟过渡方式中负荷的变化以及由负荷变化引起的发电机出力变化，将λb代入式(5)并加以调整可得连续潮流功率平衡方程如式(10)所示。

(10)

式中：PGi0、PLi0、QLi0为节点i初始发电机有功出力、负荷有功功率、负荷无功功率；bPGi、bPLi、bQLi为节点i发电机有功出力、负荷有功功率、负荷无功功率的增长方式；QGi为节点i发电机无功出力。

如果发电机节点具有无功储备，在计算过程中做PV节点处理，其无功出力取决于系统潮流分布，无法人为指定增长方式。当无功功率到达最大值，该节点转化为PQ节点。

在算法方面，可以采用连续法或直接法。连续潮流法[24]的主要优点是经过少量过渡运行方式计算便可得出极限点，缺点是每步需要大量计算，较难选取合适步长。直接法以一定步长计算各过渡运行方式，每步不需要进行预测，计算量较小，极限点与临界点间电压差别可以较小，缺点是往往在临界点以前因潮流雅可比矩阵接近奇异便不能收敛。因此可将结合两者形成一种混合潮流算法，开始先按给定步长用直接法进行计算，当接近鼻点不能收敛时，改用连续潮流法继续进行计算，最终求得静态电压稳定临界点。

3.2 直流功率增长处理方法

对直流多馈入的受端电网，本地电源相对匮乏，直流馈入功率占负荷比例较大，在负荷增长的过程中，若直流线路具有功率裕度，可进一步考虑直流功率增长的影响。

在增长方式向量b中，引入直流功率增长方式，式(10)中±Pdi一项修正为±Pdi0(1+λbPdi)，bPdi0为初始直流有功功率。与发电机无功功率类似，直流消耗无功功率属于被动变量，无法指定增长方式。

定义直流功率参与因子kdi为：

(11)

其物理含义是直流功率增长占负荷有功增长总量的比例，取值范围在0～1之间。计算时可先设定期望的直流功率参与因子，根据式(11)可得：

(12)

连续潮流计算中负荷增量总和应等于发电增量总和，考虑到直流系统送受端的交流电网电气距离较远或分别处于异步电网中，计算中将送受端的发电机分开处理，并将送端发电功率增量与直流功率增量相匹配，如式(13)所示。

(13)

式中：ΩG1为直流送端发电机节点集合；ΩG2表示直流受端发电机节点集合；ΩL为直流受端负荷节点集合；Ωd1为直流送端直流节点集合。

考虑直流系统控制模式切换，在过渡方式中，随着直流功率增加，若整流侧切换至CC(Id=Idmax)控制模式，直流功率无法再增加，则令相应的直流节点的bPdi=0， 直流送端发电机节点的bPGi=0。并根据式(13)的原则重新分配发电机出力的增长方式。直流系统其他参数因交流系统状态而越限时，控制模式依照1.3节的策略进行切换。

3.3 静态电压稳定评价标准

参照文献[25]，本文采用功率裕度KP对静态电压稳定计算结果进行评价，定义如下：

(14)

式中：Pmax、P0分别为区域负荷在静态电压稳定临界点的有功功率值、区域负荷有功功率初值。

4 算例分析

4.1 算例介绍

本文采用南方电网直流受端某区域电网作为研究对象。正常运行方式下的区域电网示意图及潮流方向如图2所示。

图2 区域电网示意图Fig.2 Diagram of the regional power grid

该区域电网共包含362个节点，63座变电站。其中500 kV变电站共5座，下送4个220 kV片区电网，初始负荷约11 534 MW。区域电网中含有本地电源6座，1座接入B片区，3座接入D片区，剩余两座分别接入1号和4、5号500 kV变电站。区域电网通过13回500 kV交流线路与周边电网相连，共有6回直流线路馈入，直流系统T通过2极线路馈入4号变电站，直流系统N通过4极线路馈入2号变电站。直流系统参数相关参数如表1所示。

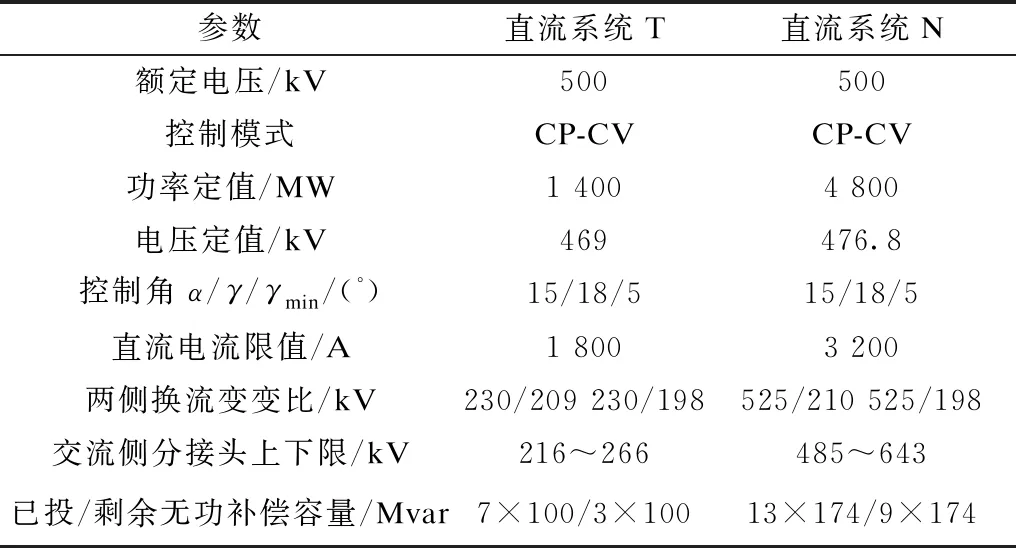
表1 直流系统基本参数Tab.1 Basic parameters of the HVDC systems

4.2 直流接入对静态电压稳定影响分析

按以下的负荷发电增长方式调整过渡方式。

1)负荷增长：区域电网负荷有功功率按初始负荷等比例增长，保持功率因数不变，无功功率随有功功率同步增长。

2)发电增长：负荷增量由本地电源优先平衡，按初始发电功率等比例增长，当本地电源功率均到达上限，由相邻区域的其他电源进行平衡。

分别采用纯交流和交直流统一迭代的方法对区域电网进行静态电压稳定分析，其中纯交流方法将直流系统简单地等效为交流电源功率注入，交直流统一迭代则考虑了过渡方式中直流系统控制模式及切换的影响。分别计算正常方式和某线路N-1下的静态电压稳定极限，结果如表2所示。

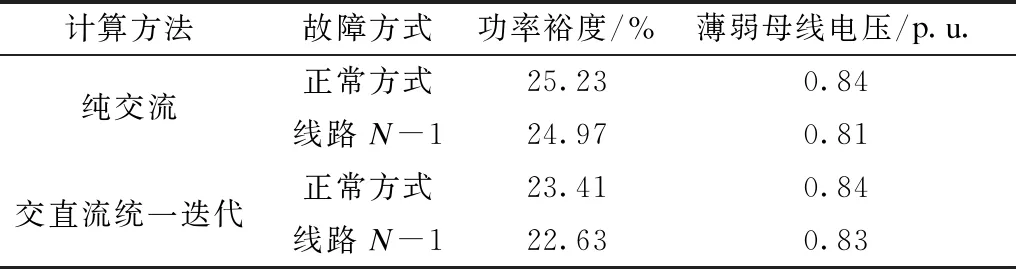
表2 不同计算方法的静态电压稳定计算结果Tab.2 Static voltage stability calculation results by different methods

在静态电压稳定极限运行点处，采用模态分析方法，可寻得系统电压薄弱母线，将薄弱母线电压绘制成PV曲线，如图3所示。

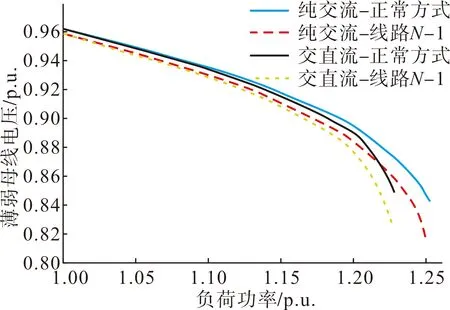
图3 不同计算方式PV曲线对比Fig.3 PV curves by different methods

当考虑直流系统模型的时候，在正常方式和故障方式下，计算所得交流系统的静态电压稳定极限均有所降低，可见直流系统的电压特性会对交流系统造成影响，下面进一步分析不同直流控制模式的影响。

4.3 直流控制模式对静态电压稳定影响分析

为了便于对比控制模式的影响，换流变分接头设为固定值，直流系统采用不同的控制模式，对上述过渡方式进行计算，结果和PV曲线如表3和图4所示。当逆变侧采用CV控制模式时，整流侧采用CP控制模式和CC控制模式等效，计算结果和PV曲线完全相同，功率裕度最高，其次是采用CC-CA控制模式，采用CP-CA控制模式是功率裕度最低。

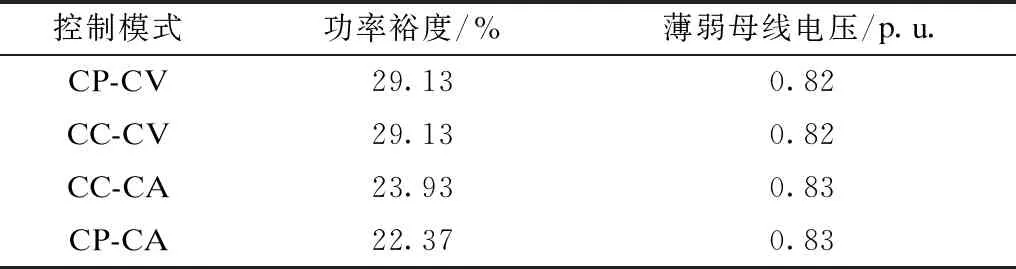
表3 不同直流控制模式静态电压稳定计算结果Tab.3 Static voltage stability calculation results by different HVDC control mode

图4 不同控制模式下的PV曲线Fig.4 PV curves by different HVDC control modes

可从逆变侧无功功率消耗的角度来分析，直流系统N逆变侧换流器无功功率消耗曲线如图5所示。

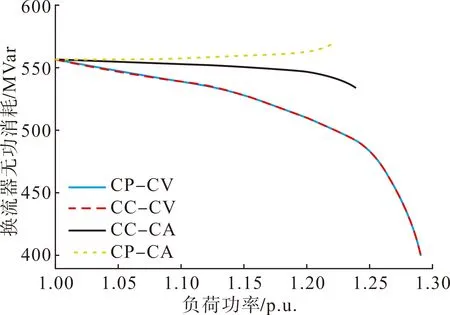
图5 不同控制模式下的换流变无功消耗曲线Fig.5 Reactive power loss curves by different HVDC control modes

根据式(1)—(3)，采用CP/CC-CV控制模式时，当交流母线电压Us下降，为保持直流电压Ud恒定，熄弧角γ减小，功率因数cosφ增大，在有功功率Pd不变的情况下逆变侧无功功率消耗Qd下降，一定程度上有利于系统电压稳定，但过小的熄弧角γ可能带来直流系统换相失败风险；采用CC-CA控制模式时，当交流母线电压Us下降，直流电压Ud随之下降，无功功率消耗会有小幅下降，但整流侧为保持直流电流Id恒定增大触发角α，从而增加整流侧的无功消耗；采用CP-CA控制模式时，逆变侧直流电压Ud随着交流母线电压Us下降，整流侧为保持功率Pd恒定增大直流电流Id，导致逆变侧无功功率消耗增加，将进一步恶化电压静态稳定。综上所述，从减小向交流系统吸收无功功率的角度来讲，采用CP/CC-CV控制模式相对具有优势。

实际运行中，在换流变分接头的协同控制下，直流系统能够保持触发角α、熄弧角γ、直流电压Ud、直流电流Id恒定，从而保持无功消耗Qd恒定，但由于分接头调节属于离散调节，当分接头调节未动作或达到限值时，直流系统的无功消耗特性仍符合上述规律，因此采用CP/CC-CV控制模式，相对有利于直流受端交流电网的静态电压稳定。

4.4 直流功率增长对静态电压稳定影响分析

根据表1，直流系统T和直流系统N距离满载工况仍有22%和25%的有功裕度，在静态电压稳定分析中考虑直流馈入功率增长的情况。直流系统均采用CP-CV控制模式，设定直流系统T功率参与因子kd分别为5%、10%、15%、20%。当本地电源功率达到上限时，由直流系统T和相邻区域电源共同平衡功率，发电机出力分配原则遵循式(13)。计算结果和PV曲线图如表4和图6所示。

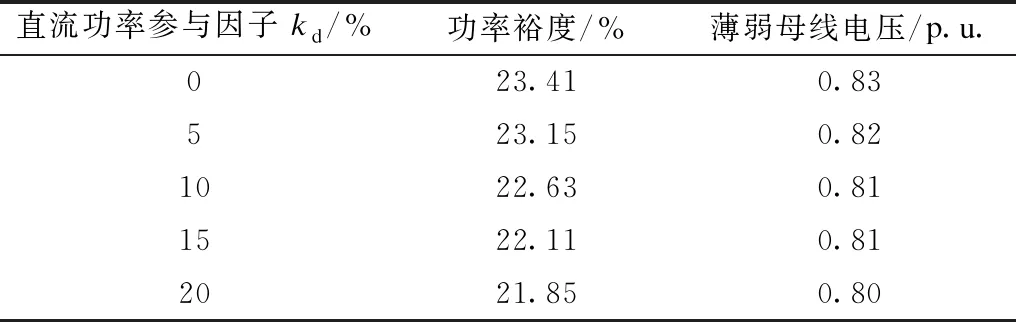
表4 不同直流参与因子静态电压稳定计算结果Tab.4 Static voltage stability calculation results by different HVDC participation factor

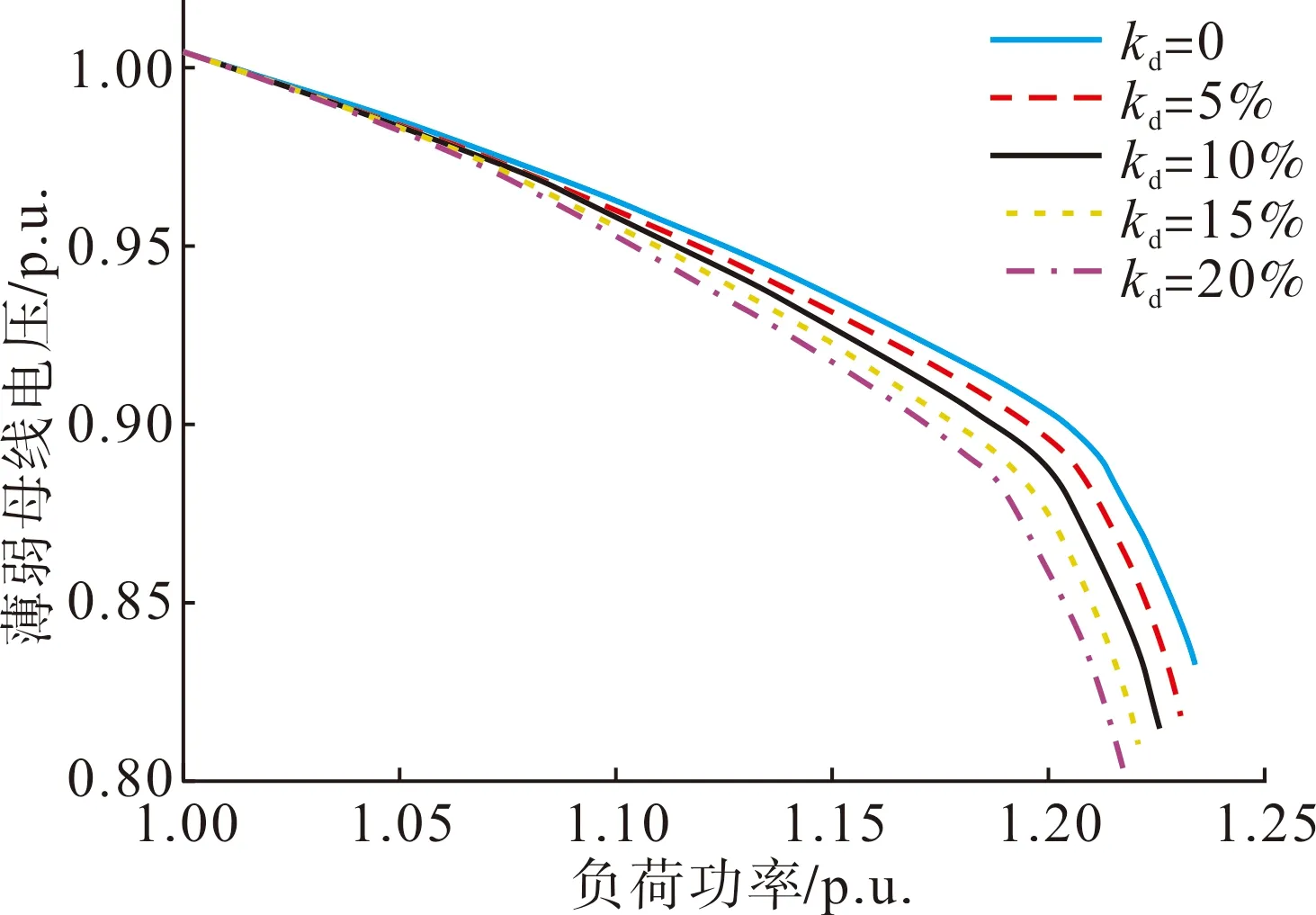
图6 不同直流功率参与因子下的PV曲线Fig.6 PV curves by different HVDC participation factors

随着直流功率参与因子的增加，受端电网静态电压稳定功率裕度逐渐减小，薄弱母线电压依次降低。直流功率在功率增量中所占的比重越大，由式(2)可知，其所消耗的无功功率随之增大，对交流系统静态电压稳定性的影响与越大。当kd=20%时，在过渡方式中直流电流已经达到上限，整流侧切换为CC(Idmax)控制模式，由于逆变侧熄弧角及变压器分接头协同控制仍有裕度，因此保持CV控制模式不变，若电压再下降导致切换为CA控制模式，由上一节的分析可知，将进一步加剧电压不稳定性。综上所述，直流系统对无功功率的大量需求及其本身在低电压时的特性，给交流系统的静态电压稳定性带来风险。

该算例中直流系统T和直流系统N的逆变侧分别剩余无功补偿容量3×100 Mvar和9×147 Mvar，下面分析无功补偿在过渡方式中对电压的支撑作用。采取最不利于静态电压稳定的方式，由两条直流系统平衡全部负荷增长功率，直至满载后再转为受端发电机组平衡。设定无功补偿在逆变器交流侧电压低于0.95 p.u.时按组投入，计算结果和PV曲线如表5和图7所示。

表5 不同增长方式静态电压稳定计算结果Tab.5 Static voltage stability calculation results by different transition mode

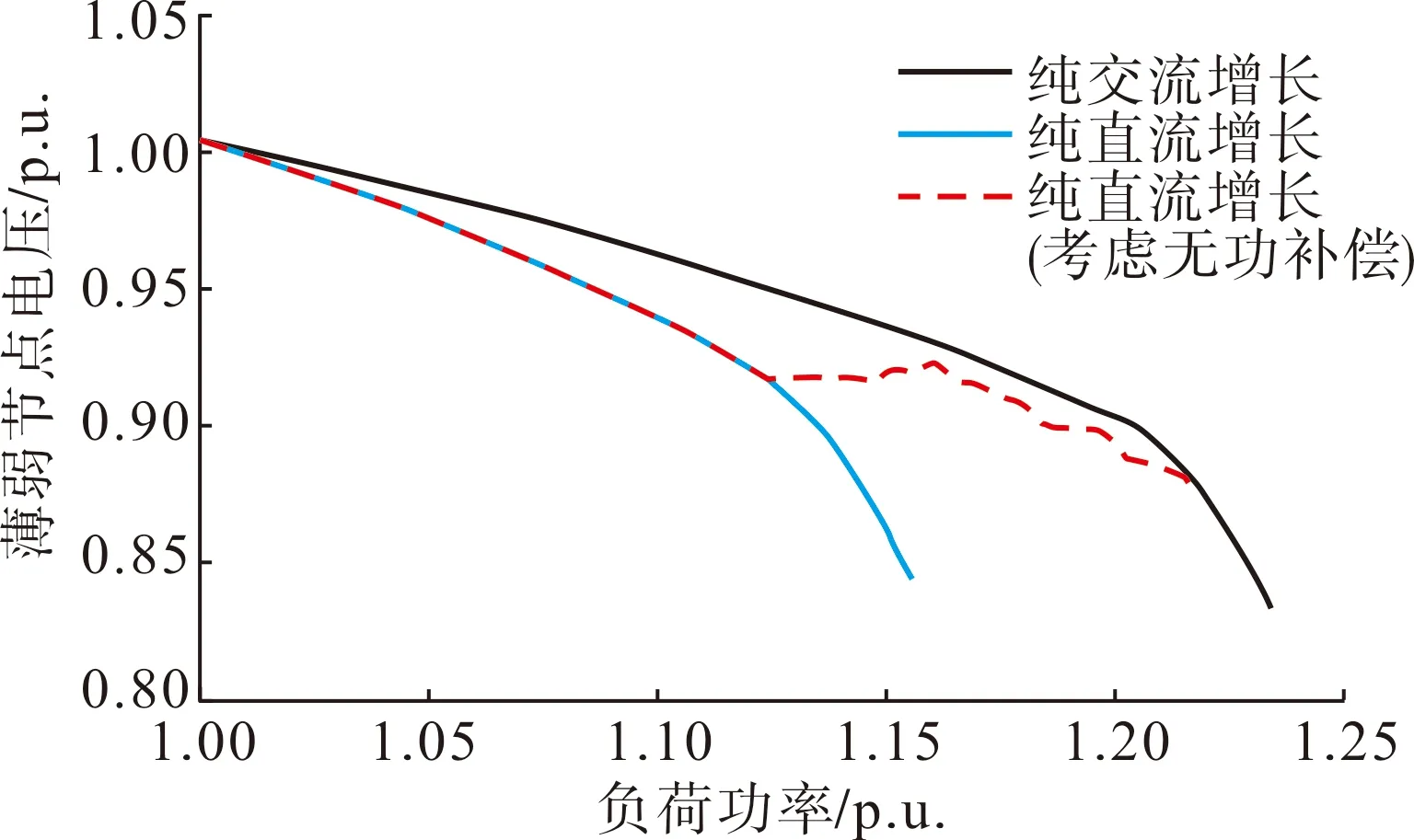
图7 不同增长方式下的PV曲线Fig.7 PV curves by different transition mode

无功补偿投入后电压支撑效果十分明显，因此计算过程中应考虑无功补偿的作用。采用纯直流功率增长时，区域电网的功率裕度仅有15.61%，无功补偿投入后功率裕度提升到21.85%，低于纯交流功率增长方式，但直流系统在过渡方式中增送功率约2 000 MW，占负荷功率增量的79%，达到满载工况，可为受端交流系统节省该部分发电机备用容量。

5 结论

直流受端电网的电压稳定特性与直流系统的控制策略和运行状态密切相关，本文深入分析直流换流器控制模式在静态电压稳定分析过渡过程中的电压响应特性，研究了换流器切换策略和计算方法，基于连续潮流法提出一种计及直流系统过渡方式的静态电压稳定计算方法，引入直流功率参与因子，可灵活分配直流功率在平衡负荷增量功率中所占比例，更全面地评估直流受端电网的静态电压稳定特性。

应用本文方法对南方电网某直流多馈入区域电网进行静态电压稳定分析，结果表明，直流系统采用CC/CP-CV控制模式，相比其他模式更有利于交流系统的静态电压稳定性；直流功率参与负荷增量功率平衡会影响受端电网的静态电压稳定性，直流功率参与因数越大，系统静态电压稳定性功率裕度越小；直流无功补偿装置投切对电压的支撑效果明显，在过渡方式中不可忽视，考虑无功补偿能够减小部分直流功率增长对电压稳定造成的影响，使计算结果更加符合实际情况。

本文所提方法，可应用于不同交直流过渡方式的静态电压稳定分析，对交直流受端电网的运行与控制具有参考价值。本文所提方法适用于含LCC-HVDC的交直流系统，随着柔性直流输电系统的逐渐投产，交直流混联系统的电压特性将日益复杂，柔性直流输电系统具有向交流系统注入无功功率的能力，在一定程度上可改善交流系统的静态电压稳定性，与上文结论将有所不同。若采用本文方法进行分析，则需对柔直系统及其电压特性进行详细建模，是本文后续的研究方向之一。