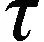基于数字多道NaI(Tl)探测器的死时间研究
闫洋洋,江 灏,蔺常勇,2,梁英超,代传波,廖 武,陈祥磊
(1.武汉第二船舶设计研究所,武汉 430205;2.武汉海王核能装备工程有限公司,武汉 430205)
任意探测器对射线(包括γ射线)的测量均存在死时间,当进入探测器的射线强度太大时,在前一个射线还未处理完而下一个射线已进入的情况时,第二个射线有可能不能被处理,产生死时间效应。在死时间效应内,系统对进入的射线无法测量,造成计数丢失[1]。在实际测量中,有时需要对计数率进行精确的测量,因此需要对死时间效应进行修正。
随着放射性测量技术的发展,数字多道的使用日益广泛,但是数字多道的工作原理与传统模拟多道不同,不同的数字多道之间的工作方式也不尽相同,产生死时间的方式也不同,对特定型号的数字多道死时间所服从的规律还需进一步研究。对于DMCA-iCore数字化多道模块,其工作时对前置放大电路输出信号进行全波形数字化采样,理论上对所有信号均完成了采集,由于所有的信号均进行了采样和保存,即使相邻两个射线间隔时间较近,射线均可以被记录。通过对信号进一步处理,丢弃掉波形发生重叠、无法准确测量的信号,从而产生测量的死时间。死时间的产生原理与模拟多道完全不同,下文中对该数字多道死时间服从的规律进行研究。数字多道同时会给出测量过程中的实时间与死时间,文中对数字多道给出的死时间也进行了分析研究。
本文以DMCA-iCore数字化多道模块与NaI(Tl)探头为基础,对该数字多道死时间效应的产生原因进行了理论分析,得出数字多道死时间也服从扩展型分布的结论。本文后续对修正方法进行了研究,提出基于牛顿迭代法的修正函数,并且使用双源法对死时间进行了测量,最后在137Cs标准剂量场中验证了修正方法的有效性。
1 探测器死时间理论分析
在放射性测量中,相隔最近、分别能引起系统计数的两个脉冲之间的时间称为系统的分辨时间,也叫死时间。对于传统的模拟多道,死时间通常有两类[2-4]。
第一类,扩展型: 在第一个脉冲到来之后的死时间τ内,第二个脉冲不会被记录,但是第二个脉冲会引起同样的死时间,即延续了系统的失效时间。第一类死时间表示为:
m=nem
(1)
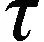
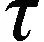
m=n/(1-n)
(2)
1.1 数字多道工作原理
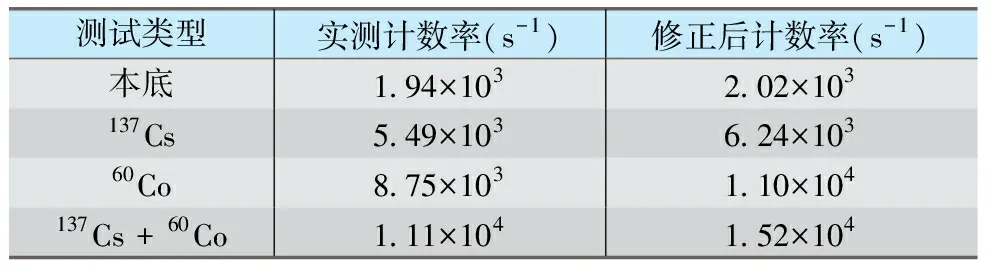
本文中的NaI(Tl)探头体积为2 L,尺寸50 mm×100 mm×400 mm。DMCA-iCore数字化多道模块通过梯形滤波后得到信号的幅度信息,梯形上升时间为2 μs,平顶时间1 μs,下降时间2 μs。具体工作方式为:前置放大电路输出的信号,经过数字多道进行波形采样。采样后的信号分为两路:一路为快信号处理通道,信号脉冲宽度很窄,此通道测量信号之间的时间间隔Δt;第二路为脉冲成型通道,对采样得到的数字化信号进行梯形滤波。梯形滤波可以有效提高信号的信噪比,提高谱仪的能量分辨率。对信号之间的时间间隔Δt设置适当的阈值T,当相邻信号之间的间隔Δt 图1 数字多道工作方式示意图 由于对信号进行了丢弃处理,所有的辐射事例信号未能全部测量,因此系统产生死时间效应。对计数率进行精确测量时,需要对死时间效应进行修正处理。 数字多道同时计算出堆积信号的结束时间,如图1中Δt1所示,Δt+Δt1为数字多道给出的测量过程中的死时间,根据死时间与测量实时间的比值,可以计算得出死时间比例系数。 辐射信号时间间隔服从泊松分布,两个信号时间间隔Δt大于或等于时间T的概率为[5]: P(Δt≥T)=exp(-mT) (3) 式中,m为真实辐射信号的平均计数率。 对于目前多道的工作原理,当信号发生堆积时会被丢弃,因此一个辐射信号被测量到需要满足两个条件:(1)该信号与前一个信号的时间间隔Δt≥T;(2)同时该信号与后一个信号的时间间隔Δt≥T,即该信号与前后相邻的信号均没有发生堆积时才会被探测到。T为判断信号发生堆积的时间阈值。 考虑到与前后相邻信号的时间间隔相互独立,满足测量条件时,被测量到的概率为: P=[exp(-mT)]2=exp(-2mT) (4) 因此单位时间内记录到的平均脉冲数n为: n=m×exp(-2mT) (5) 式(1)与式(5)为隐函数,无法直接作为修正函数使用。对于常用的修正方法,一般是在计数率不高时,对式(1)做泰勒公式展开,取第一项作为修正函数,即对式(1)与式(5)进行了近似处理,此时需要满足m≪1,修正函数表示为: m=n/(1-n)≈n(1+n) (6) 本文中NaI(Tl)探测器死时间预计为几十μs左右,在计数率超过104/s时,m≪1的条件已无法满足。本文以牛顿-拉夫逊方法(也叫牛顿迭代法)(Newton-Raphson method)为基础,推导出相应的修正函数。 牛顿-拉夫逊方法为牛顿提出的一种近似求解方程的方法,通过迭代计算的方法寻找方程f(x)=0的根。首先选用x0为f(x)=0的一个近似根,过点[x0,f(x0)]做曲线y=f(x)的切线L,L表达式为: y=f(x0)+f′(x0)(x-x0) (7) L与x轴交点的横坐标: x1=x0-f(x0)/f′(x0) (8) x1为根的一次近似值,重复以上过程,得到根的近似值序列: xn+1=xn-f(xn)/f′(xn) (9) 对式(1)进行求解,令f(m)=nem-m;则f′(m)=nem-1;计算f(m)=0的根可以得到真实计数率的近似值,从而实现对系统死时间效应的修正。 为了避免迭代过程的收敛性问题,本文中只使用一次迭代,初始值m0=nen;根据探测器的实测计数率n,计算得到真实计数率的近似值m1,该近似值m1作为死时间修正后的结果为: (10) 基于双源法测量死时间为利用两个独立的放射源,分别测量各自的计数和两个源的合计数。测量一个源时要将另一个源屏蔽起来,但每次放置放射源时不改变他们的位置[6]。假定死时间与射线能量无关,使用137Cs源与60Co源进行了测试。 (1)首先设定好实验条件,确定NaI(Tl)探测器测量谱满足温飘控制要求后进行本底测量,本底计数率的测量值为nb; (2)将137Cs源放置在固定位置,测量NaI(Tl)探测器的137Cs能谱及实测计数率n1; (3)将137Cs拿走后屏蔽,将60Co源放置在某固定位置,测量60Co源能谱及实测计数率n2; (4)最后将137Cs与60Co均放置在原来的位置,测试137Cs与60Co共同的能谱及实测计数率n12。 使用死时间修正函数式(10)对测得的计数率进行修正,修正后的结果分别表示为:本底计数率mb,137Cs源计数率m1,60Co源的计数率m2,两个源时总的计数率为m12。根据双源法的测量原理,修正后的计数率应满足下式: m1+m2=m12+mb (11) 定义函数g()=|m1+m2-m12-mb|,g()=0时对应的值即为NaI(Tl)探测器的死时间。函数g()与之间关系曲线如图2所示,g()=0时对应的值约为20.6 μs。 图2 函数g()与关系曲线图 表1 NaI(Tl)探测死时间修正结果 在标准辐射剂量场对NaI(Tl)探测器进行了测试,辐射剂量场使用的137Cs源,扩展不确定度为6.8%,在NaI(Tl)探测器的测量范围内选取了适宜的剂量点进行了测试,包括3.52×10-7Gy/h、5.88×10-7Gy/h、9.73×10-7Gy/h三个剂量点。根据理论分析,NaI(Tl)探测器的净计数率应与剂量率成正比关系,对原始数据净计数率、多道给出的死时间修正后的净计数率、迭代法修正后的净计数率三者进行修正与比较。对测量结果进行最小二乘拟合,净计数率与剂量率之间的关系如图3所示,计算中扣除了相应的本底计数。在未进行死时间修正时,三个点剂量率的相对偏差值分别为:1.63%、-2.03%,0.55%,拟合相关系数为0.996 7;使用多道给出的死时间修正后,三个点剂量率的相对偏差值分别为:-2.19%、2.3%、-0.58%,拟合相关系数为0.998;使用迭代法修正后相对偏差值分别为:0.71%、-0.8%、0.2%,线性拟合相关系数为0.999 7。迭代法修正后相对偏差值大大减小,并且相关系数更接近于1,计数率线性最好,证明死时间修正是有效的。 由图3可以看出:修正之前,在高剂量率9.73×10-7Gy/h处,计数率明显偏低,导致曲线线性变差;使用多道给出的死时间进行修正后,在高剂量率9.73×10-7Gy/h处,计数率明显偏高,产生过修正;迭代法修正后计数率线性度最好。 图3 净计数率与剂量率关系图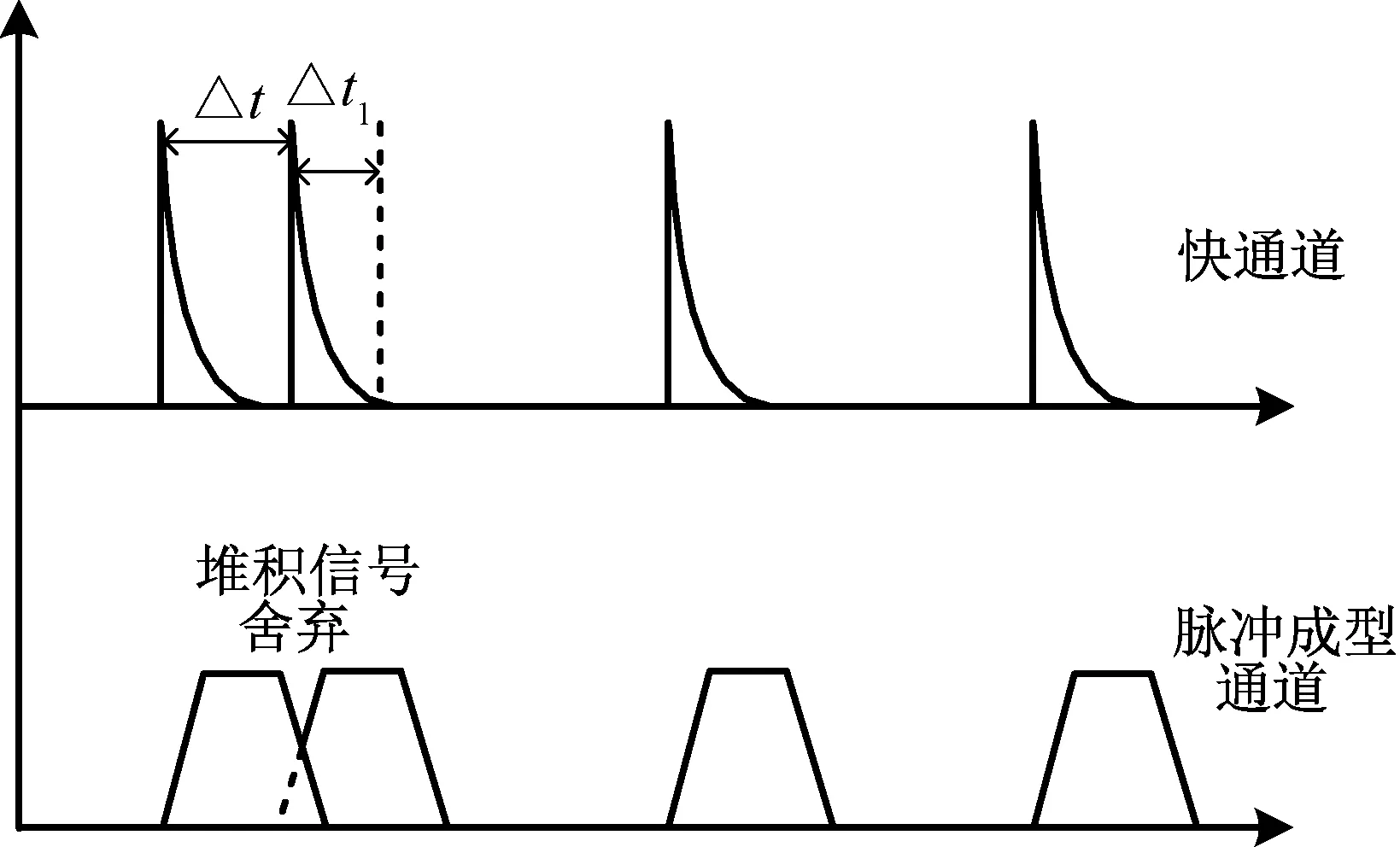
1.2 数字多道死时间规律研究
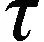
1.3 死时间修正
2 基于双源法测试死时间

3 标准辐射剂量场测试

4 结论