指甲电子顺磁共振(EPR)波谱解析的数学模拟研究
阎长鑫,刘玉连,焦 玲,张文艺
(中国医学科学院北京协和医学院放射医学研究所,天津 300192)
随着核能利用的增加,核与辐射带来的潜在危害也在增长。在事故发生时快速、有效的回顾性剂量测定也就变得更加重要[1]。电子顺磁共振[2-3](electron paramagnetic resonance,EPR)谱是评估吸收剂量方法之一,它是基于对辐射引起的生物或物理效应的分析。这些效应会产生相应的自由基,这些自由基的浓度取决于吸收剂量。人体中的牙齿、骨骼和指甲经过辐照后都会产生相应的自由基。其中牙齿和骨骼中的碳酸羟基磷灰石因辐射产生的自由基十分稳定,长达107a之久。但牙齿与骨骼的处理较复杂,且会对取材者造成一定的伤害,所以研究者一直在寻找可以替代牙齿、骨骼的材料。指甲作为非侵入、收集方便的一种生物材料,得到研究者的关注[4]。
指甲中含有大量的α角蛋白[5],当受到电离辐射的时候会产生自由基,EPR图谱中,指甲中自由基的含量(浓度)可由图谱二次积分(所围面积)来表示,即自由基浓度越高,图谱所围成的面积越大,因此可以利用两者的关系来进行剂量估算[6]。
指甲受到电离辐射后,会产生辐射诱发信号(radiation-induced signals,RIS),根据其产生原理不同分别将其命名为RIS1~RIS5。人体的受照剂量一般不会超过50 Gy,因此我们只对两个较低剂量区的RIS感兴趣,RIS2与RIS5。但是并非只有电离辐射会在指甲中产生自由基,Chandra H等[7]发现剪切后的指甲EPR图谱显示:“剪切”产生了信号,并将其命名为机械诱发信号(mechanically-induced signals,MIS),即剪切信号。由于部分MIS信号与RIS信号位置相同(g值一样)或是在其附近,在EPR图谱中会重叠在一起。对于利用RIS信号进行剂量估算来说,MIS是一个干扰信号,应将MIS信号除去。除了上述RIS与MIS信号外,其他信号被称为本底信号(background signal,BKG)。完成估算的重点在于将RIS从重叠在一起的信号中分离出来,与剂量建立关系,映射到坐标轴上建立剂量回归曲线。Romanyukha 等[8]比较了各种去除MIS的化学方法,相比之下,D,L-二硫苏糖醇处理效果比较好。王宏力等人[9]比较了静置法、浸泡法、毛刷法和滤纸法,提出用潮湿滤纸包裹指甲去除MIS效果最佳。赵徵鑫等[10]给出了剂量重建中误差来源的分析,张腾达等[11]给出了定量测量理论,为剂量定量分析和剂量回归曲线的建立提供了基础。
传统的估算方法是将照射已知剂量EPR谱线减去未照射剂量EPR谱线(0 Gy),达到去除本底的目的,将其差值作为受照剂量谱线,并对谱线的峰峰值进行计算,将其对质量与标样(g-marker)峰峰值做归一化处理,此方法称为谱减法。本研究提出拟合法即通过数学模拟的方法解谱以去除本底来降低误差,这种研究方法将辐照后指甲EPR信号视为由BKG与RIS两种信号叠加,利用数学模型来模拟BKG与RIS得到两个模型函数,这两个模型函数通过线性组合来拟合EPR信号。本研究同时对RIS不同组成进行了模拟,包括RIS2+RIS5和只有RIS5的两种情况。对于每一个受到已知剂量照射的指甲EPR谱,通过拟合计算出BKG与RIS在受照波谱中的面积占比,其中RIS面积占比用来表征吸收剂量,即从受照波谱中去除了BKG,建立剂量与RIS面积占比的回归曲线。
1 材料与方法
1.1 样品采集
实验所用指甲样品3组来自天津市(2男,1女,年龄20~55岁之间),对其编号为A、B、C;2组来自河北省(每组约10人混合指甲,平均年龄40岁),编号为D、D-RIS5。使用同一把指甲刀进行剪切,剪切后储存在-18 ℃冰箱中或立即处理。
1.2 样品处理
(1)实验1——RIS2+RIS5的EPR波谱分析实验
对收集的4组样品(A、B、C、D)进行剪切,尺寸为2 mm×2 mm,同一个人的十个手指的指甲随机分成8份,每一份约20 mg,剪切后全部混合以20 mg为标准取8份,其余样品放于冰箱保存留用于其他实验。因为湿滤纸包裹后,会出现指甲粘在滤纸上的现象,不方便转移,本文直接在小烧杯中用蒸馏水对样品浸泡10 min,去除剪切信号(MIS),使用真空干燥箱(予华 DZF-6050型)对其进行干燥,条件70 ℃,-0.1 MPa,干燥1 h,用于去除由于浸泡指甲所引入的水,并对水处理后的样品进行称重处理,称重后对每组7份样品进行照射,每组预留一组作为本底对照(记为0 Gy),照射后记录其EPR波谱。
(2)实验2——RIS5的EPR波谱分析实验
收集10人混合指甲,编号D-RIS5,以每份30 mg,分为13份,12份进行照射,剩余一组作为本底(0 Gy),照射后将13份样品进行剪切,尺寸2 mm×2 mm,蒸馏水浸泡10 min,真空干燥1 h,样品处理后进行EPR测量,模拟真实照射事故场景下的剂量分析(即:照射后再剪碎)。
1.3 样品照射
将样品放入透明自封袋中用137Cs源根据不同实验要求在室温下进行照射。放射源使用的是加拿大Gammacell-40型137Cs伽马射线源(剂量率为0.88 Gy/min),均匀照射,放射源有出厂标定且每年进行实验验证。对于实验1中A、B、C、D中每组7份样品分别照射1,2,3,5,8,10,50 Gy。对于实验2的D-RIS5组12份样品分别照射5,10,15,20,25,30,35,40,45,50,55,60 Gy。
1.4 样品EPR测量
本次研究采用的仪器是德国布鲁克公司生产的X波段的电子顺磁共振波谱仪(型号为A300)。定量研究采用ER 4119HS-2100 marker accessory作为标样,以相对信号面积进行分析。实验具体条件:中心磁场3 530 G,扫场宽度150 G,调制频率100 kHz,调制幅度5 G,时间常数40.96 ms,扫描次数10,微波功率1.01 mW,扫场时间83.89 s,实验温度24 ℃左右,相对湿度40%。
1.5 模拟方法
用于模拟的基本函数为高斯函数的一阶微分:
式中,A为峰峰值的一半;X0为函数中心(磁场中心,可通过,g=0.714 477 36×v(MHz)/X0转换为g值,其中v为频率);Hpp为线宽;X为谱图横坐标即磁场值,单位均为G。模拟时通过原图谱提供A、X0、Hpp初始值用于后续迭代,三个数值越接近原谱线真实值迭代次数越小,所用时间越少。
用该函数来分别模拟预留本底(0 Gy)与50 Gy(对于实验2为60 Gy)的高剂量图谱,预留本底(0 Gy)模拟结果作为纯净本底的模型函数记为LBKG,50 Gy模拟结果作为只有RIS信号的模型函数记为LRIS,LRIS的模拟选用高剂量的原因是因为在高剂量条件下可忽略本底影响而将其模拟结果作为纯RIS模型函数,此处出于人体实际受照情况选用50 Gy(实验2为60 Gy)。得出两个模型函数后,对于受到已知照射剂量谱图都可通过LBKG与LRIS的线性叠加表示,即F=A0×LBKG+B0×LRIS,其中F为已知剂量图谱函数,A0,B0分别为LBKG和LRIS的面积贡献。对于吸收谱线(高斯函数)的面积计算可通过高斯函数一次微分中参数进行计算,Dy为峰峰值(波峰纵坐标与波谷纵坐标的差值),S为吸收谱线的面积:
S∝Dy×Hpp2
1.6 模拟流程
利用布鲁克Acquisit软件获取样品EPR图谱,测得图谱以ASC文件导出。在Windows 10 平台利用免费的Visual Studio 2019社区版作为开发IDE处理ASC文件,程序语言选用C++。画图利用平台调用Python的matplotlib[12]。
模拟流程如图1所示。将实验得到的图谱保存为ASC文件,将文件导入程序,程序先对未照射样品(0 Gy)图谱进行模拟,先提取图谱的特征部分,包括信号的峰-峰值(Dy),线宽(Hpp),以g=2.005,Dy,Hpp为非线性最小二乘(Levenberg-Marquardt)的输入,通过高斯函数的一阶微分对未照射样品的波谱进行模拟,得到LBKG(理论本底波谱);以同样方式模拟高剂量波谱(实验1为50 Gy,实验2为60 Gy),得到理论高剂量波谱(LRIS),将两个理论波谱进行保存,为之后的模拟做准备。
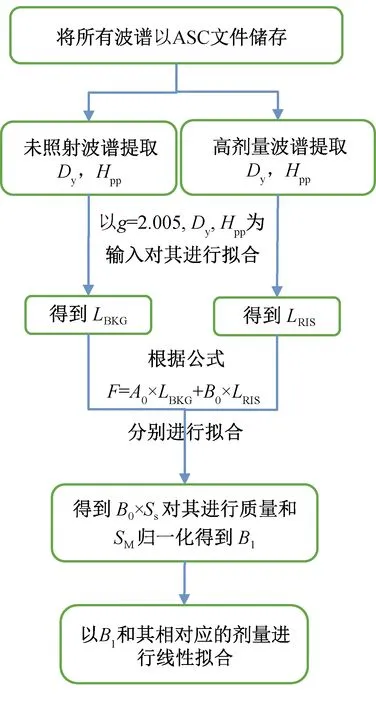
图1 模拟流程图
将每组样品中除0 Gy与50 Gy(实验2为60 Gy)的图谱分别导入程序中,对于每个波谱提取波谱频率、g-marker(标样)的面积(SM)、样品质量(m)和样品剂量(后两项存储在图谱文件名中),并在组内按照剂量从小到大进行排序,按照每个波谱的频率在g=2.005的位置产生之前保存好的LBKG,LRIS,并利用公式F=A0×LBKG+B0×LRIS对其进行非线性最小二乘拟合。B0乘吸收谱线面积(Ss)对质量和SM进行归一化处理得到B1,将剂量作为横坐标,B1作为纵坐标做线性拟合,其流程如图1所示。对于每一组样品分别利用组内0 Gy与高剂量得到组内LBKG与LRIS,以消除个体差异。
为了得到较为纯净的LRIS,本实验在选用较高剂量的同时,在构建LRIS之后,再从LRIS中扣除LBKG,因此高剂量纯净波谱是由模拟得到的LRIS与LBKG模型函数的差值,作为新的LRIS,记为L′RIS,即L′RIS=LRIS-LBKG。
2 实验及模拟结果
指甲经过离体剪切和剪碎过程(方便装入内径4 mm石英管中)中会产生MIS,而实验研究表明水处理会消除MIS[13]。经过水处理干燥后未照射(0 Gy)的样品作为本底信号BKG,模拟效果最优的波谱作为LBKG,其EPR图谱与模拟如图2(a)所示。经过水处理干燥后照射50 Gy,得到高剂量波谱。50 Gy图谱模拟及其模型函数LRIS如图2(b)所示,图2为示例组模拟图,实验组BKG与RIS的模拟参数列于表1。判断模拟精度的标准为残谱(实验谱与模拟谱的差值)的平均值与标准偏差,从表1中可以看出对于B组BKG残谱平均值占图谱峰峰值的0.050 1%,RIS2+RIS5残谱平均值占峰峰值0.006 90%。残谱平均值所占比例比较小,其标准偏差只有少数超过图谱峰峰值的10%。因为残谱数值有正有负,取平均值会相互抵消,因此残谱平均值较小,但标准差不会抵消,数值较大。在模拟两个模型函数时,拟合感兴趣区域在信号部分,意在得到信号部分的线型,即得到信号部分峰峰值与信号部分的线宽,因此得到的残谱与实验谱g-marker重合,为了消除残谱平均值与标准偏差计算时g-marker的影响,将感兴趣区域取在3 490~3 530 G之间。
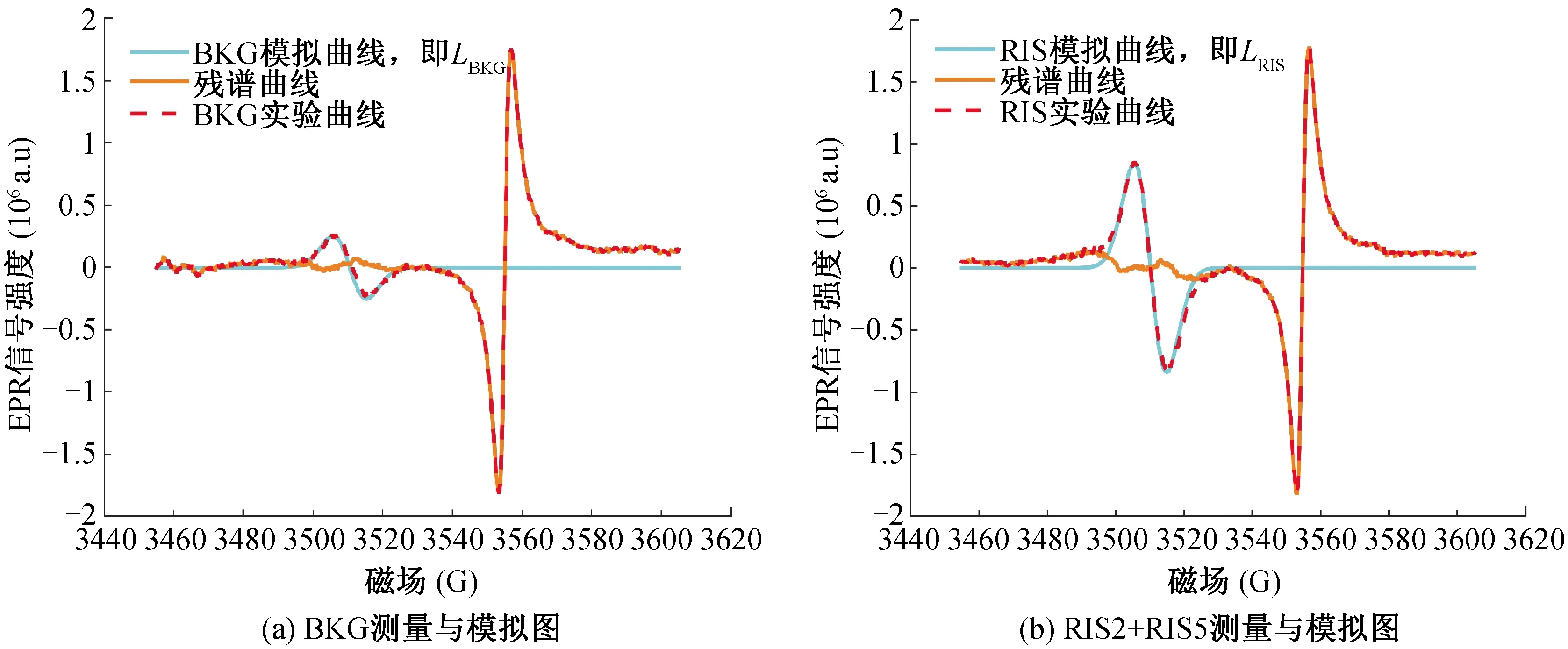
图2 示例组单人样品的BKG与RIS(50 Gy)的EPR测量及模拟图谱

表1 EPR波谱拟合参数
利用对应组产生的LBKG与LRIS作为F=A0×LBKG+B0×LRIS中的输入,对导入的实验波谱进行拟合,A组拟合结果如图3所示。A组中利用B1(B1=B0×Ss/(Sm×m))与照射剂量做剂量回归曲线(图4),回归方程为y= 0.004 59x+0.035 6,R2=0.941 432,拟合误差=0.719 Gy。其他4组的拟合结果列于表2,从表2可以看出,同一个人的指甲所做的样品线性度较好(R2>0.9),拟合误差在1 Gy以下(A、B、C组),而对于10人混合样品,线性度相对一人组样品线性度稍差,拟合误差在1 Gy左右(D组)。表2中D-RIS5组为实验2的结果,从中可以看出拟合法线性度与拟合误差都优于谱减法。表3给出两种方法的A、B、C、D四组各剂量值下的相对偏差,给出数据中大部分拟合法的剂量准度优于谱减法,只有6个点谱减法相对拟合法相对偏差更小,总体来说拟合法估算值与照射值之间偏差小于谱减法。

图3 A组2Gy拟合图谱
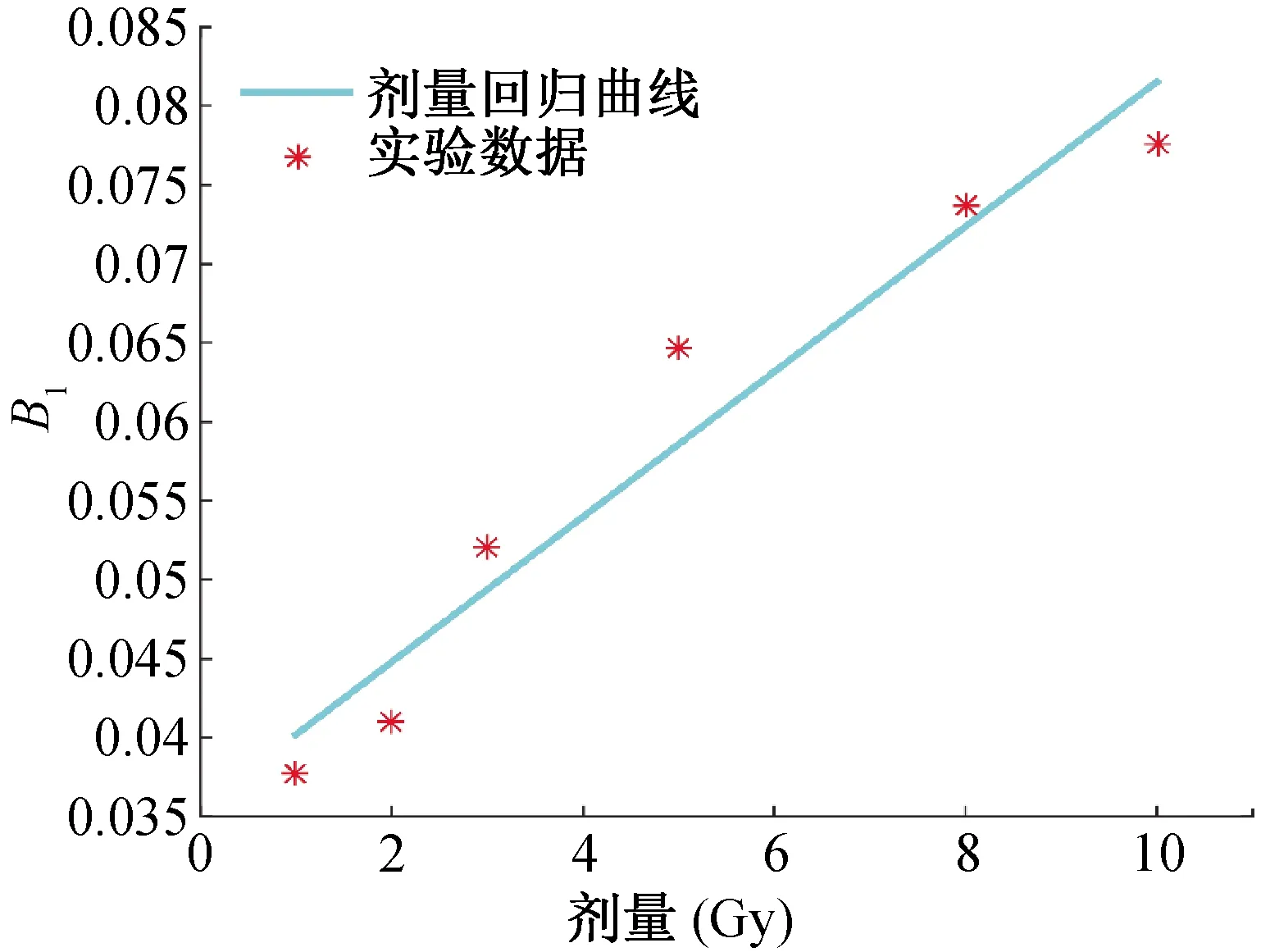
图4 A组剂量回归曲线

表2 EPR波谱拟合结果
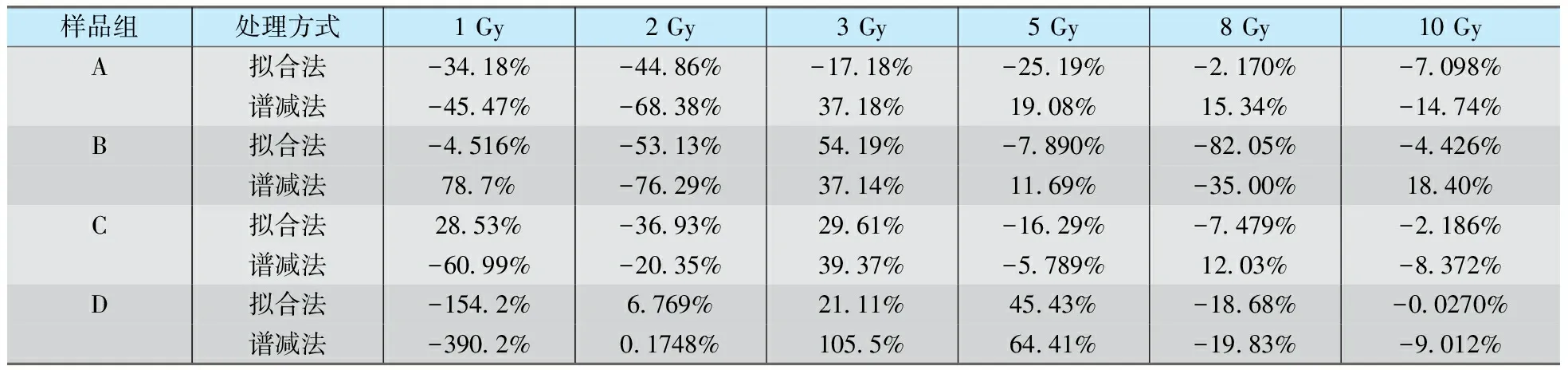
表3 拟合法和谱减法与照射剂量的相对偏差1)
3 讨论
在2008年突尼斯,2010年加蓬,2012年秘鲁的192Ir事故[14]中,研究人员利用指甲作为生物材料对事故进行了剂量估算,事故中利用RIS5完成了回顾性剂量测定。Romanyukha[15]利用健康人的指甲建立“通用”剂量回归曲线,这种方法利用Reyes[16]提出在保证样品尺寸与含水量相同的条件下,样品的剂量响应很类似,这也为快速剂量估算提供了方法。上述方法都是利用的谱减法进行估算,并没有从波谱分解上对图谱进行解析。而本研究通过控制水处理与照射先后顺序,分别对RIS2+RIS5与RIS5从图谱组成上进行了模拟,实验1在水处理之后进行照射,所得辐射信号为RIS2+RIS5,而实验2经过照射后水处理会去除RIS2[17],水处理操作后辐射信号只有RIS5,即所测得的图谱信号是本底与RIS5的叠加[18]。
在实验中,每一次测量的图谱g值有轻微浮动,同时部分波谱也会出现上下浮动的情况,因此实验中将拟合所用的高斯公式进行相应的改进,对高斯公式加入了垂直移动分量与水平移动分量,使拟合结果更加完善。而对于D-RIS5的估算,预测误差相对其他较大,在照射相差5 Gy时才能明显看到谱图差别,在以后的研究过程中也会探究提高探测精度的方法,为辐射事故作出更好的分型分度。同时由于指甲样品在磁场方向上的各项异性原因,可考虑将样品分3个角度进行测量,测量后取平均值来消除各向异性的影响。对于多人D-RIS5组拟合法与谱减法的剂量估算准确性列于表4,拟合法只有少数剂量点优于谱减法,分析其原因可能是由于60 Gy与0 Gy信号区分度并不是很大,60 Gy峰峰值约是0 Gy的2倍,扣除后近似1∶1进行拟合,所以拟合效果没有其余4组好。虽然可以继续提高RIS5的照射剂量,但是文献[17]指出RIS5在28 Gy到60 Gy之间存在饱和,继续增加剂量谱线将成下降趋势,更加难分辨RIS5与本底。

表4 D-RIS5组拟合法和谱减法与照射剂量的相对偏差
4 总结
本研究编程实现拟合法,先对两个预设谱图进行模拟,模拟过程中先对目标谱图进行特征提取,包括g值、峰峰值、线宽、频率和质量,提取后根据峰峰值、线宽对目标进行非线性最小二乘模拟,在残谱最小时,保存模拟得到的谱图函数(两个函数∶本底与高剂量),利用模拟的两个函数通过线性叠加拟合已知剂量图谱,计算出高剂量函数在其中占比,再将占比乘高剂量函数面积,之后对其分别进行质量、g-marker面积归一化,并与剂量进行线性最小二乘拟合得出剂量回归曲线及参数。
将EPR图谱重叠部分进行分解一直都是波谱解析的难题,本实验利用编程实现了对水处理后指甲信号的解析,相对于传统的谱减法,本实验方法从波谱组成上进行了解析,同时利用面积代替传统的峰峰值,减小因线宽变化所带来的误差,同时编程也大大缩短了计算所用的时间,节省人力。Trompier[19]指出RIS5+RIS2与剂量的线性度高达125 Gy,在本实验中利用RIS总(RIS2+RIS5)进行估算时,在0~10 Gy范围内,个人样品R2大于0.9,拟合误差最低在0.6 Gy,多人组样品R2接近0.9,相对误差总体优于谱减法。对于利用RIS5在0~60 Gy进行剂量回归的R2大于0.9,拟合误差4.78 Gy。
综上,本文通过编程以高斯函数一阶微分作为模型,Levenberg-Marquardt作为算法从谱线组成上对图谱进行解析,分解出其中辐射诱发部分与已知剂量形成坐标对投射到坐标系中完成剂量估算。相对于传统关心图谱峰值的谱减法,拟合法将图谱线型考虑在其中,对于RIS2+RIS5拟合相比于谱减法,精度与准确度较好,为指甲EPR图谱去除本底之后做剂量估算提供了一种方法。

