一种两栖运载机器人水陆运动性能研究

王永敢, 张俊敏, 王永娟, 向宇, 倪肖杨

(1.南京理工大学 机械工程学院, 江苏 南京 210094; 2.中国兵器工业第208研究所, 北京 100081)

随着机器人技术的发展，一些用于运载、侦察、探测等用途的机器人不断涌现[1-3]，但这些机器人一般只适应单一的陆地环境，而对于战场上的水面环境则难以适应，因而设计一种具有一定越障能力、一定水面行驶能力的机器人作为运载平台显得尤为重要，结合履带式机器人及船的结构特点设计了一种水陆两栖机器人作为运载平台。所设计的水陆两栖机器人(以下简称机器人)需满足水陆运动的一些性能。因此对该水陆两栖机器人进行水陆运动性能研究以提高水陆运动能力。本文在所设计的水陆两栖机器人基础上，主要从步态规划的角度进行陆地的爬台阶能力分析，并基于动力学规律寻找机器人受强瞬态冲击保持稳定性的条件，最后采用数值仿真的方法对机器人水中行驶阻力、行驶压力进行分析。

1 陆地爬台阶能力分析

1.1 机器人模型

设计的水陆两栖机器人如图1所示，前后摆臂履带具有绕摆臂轮旋转360°的活动角度，通过履带摆臂之间的任意夹角组合可实现机器人步态的变化，机器人爬台阶的高度不仅受自身结构参数的影响，而且还与爬台阶时的步态有关，对机器人爬台阶步态进行研究以发挥机器人爬台阶的最大能力[4-7]。

图1 水陆两栖运载机器人

1.2 质心变化关系

机器人前摆臂L1,摆臂L2与中间履带L的夹角变化使机器人质心发生变化。以xoy为牵连坐标系,模型如图2所示,履带L轴线绕履带L2轴线逆时针旋转方向夹角为正,履带L1轴线绕履带L轴线逆时针旋转方向夹角为正。

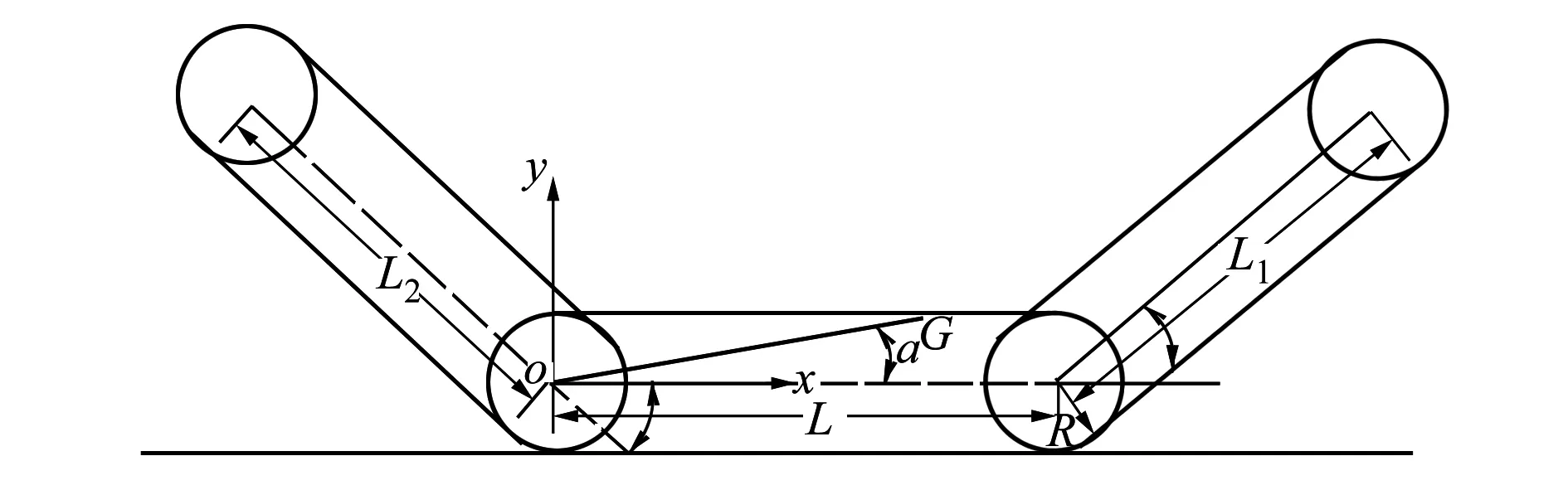
图2 机器人行走履带

机器人质心坐标与履带摆臂夹角关系如下：

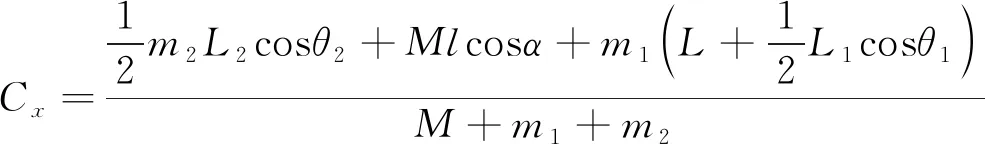
(1)

(2)

式中：M为机器人主体质量；m1,m2为两摆臂质量；L为中间履带长度；L1为前摆臂长度；L2为后摆臂长度。主体质心为G,R为带轮半径,θ1,θ2为履带关节夹角。

1.3 爬台阶步态规划

机器人爬台阶分为2个过程,第一过程是攀爬台阶,即前履带接触台阶棱线,此过程中使机器人质心升高;第二过程为翻越台阶,使机器人质心越过台阶垂直面,而保证机器人不会发生倾倒。

机器人爬台阶步态的规划实质上是对摆臂履带之间的夹角进行规划。为了兼顾爬台阶能力与效率,低台阶时,以图3步态使其爬台阶效率更快,高台阶时,以图4步态使其爬行能力更大,爬高台阶与低台阶的区别在于攀爬过程,高台阶攀爬时后摆臂支撑使质心最大程度升高,如图4中c)～f)所示。

图3 机器人爬低台阶步态规划

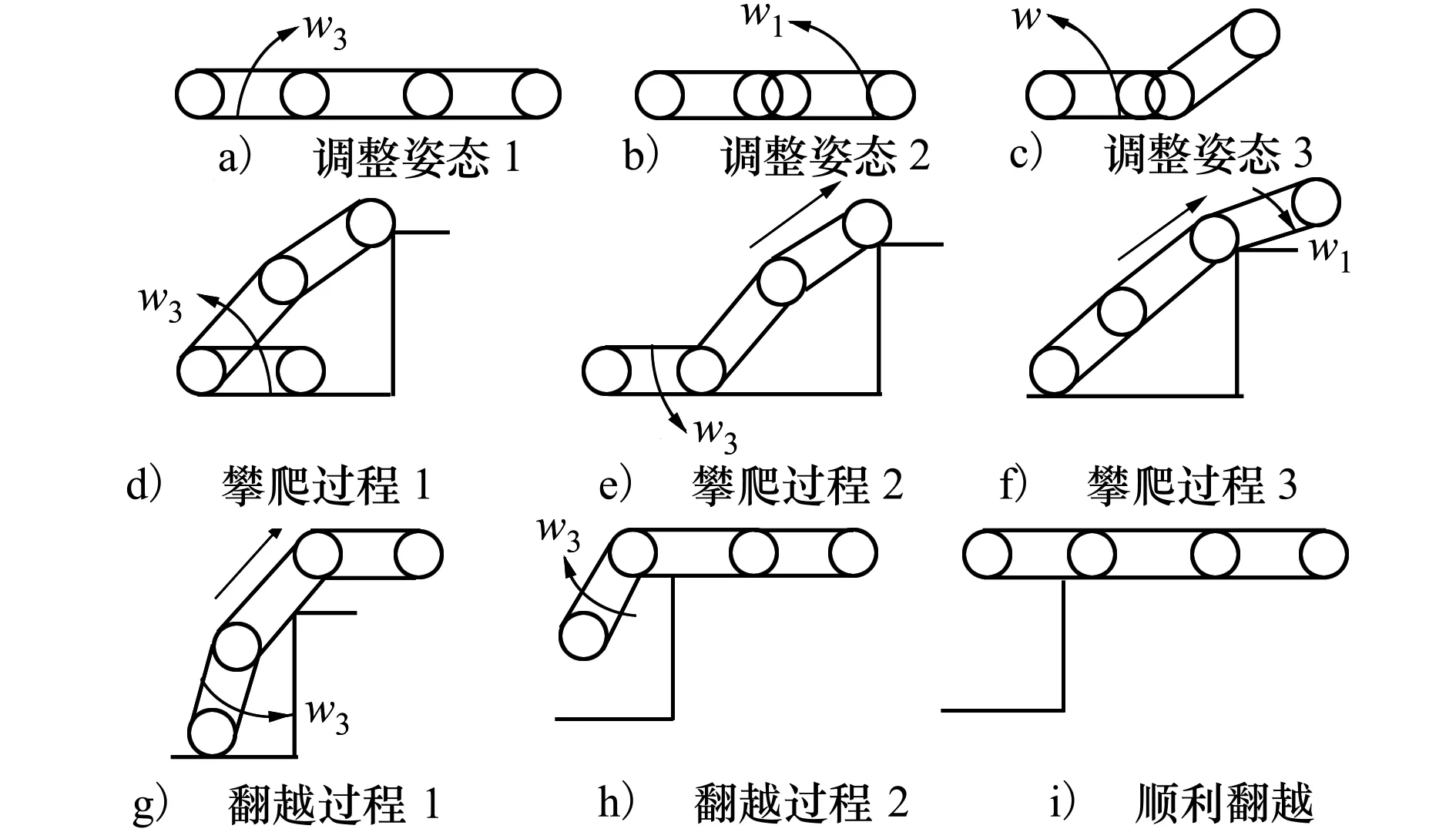
图4 机器人爬高台阶步态规划

1.4 攀爬台阶运动学建模

履带机器人攀爬台阶高度取决于摆臂的有效半径,当前摆臂有效半径大于台阶高度时,才能成功攀登台阶[8],如图5所示。

图5 机器人攀爬低台阶示意图

攀爬台阶高度h与前摆臂有效半径Re如下所示：

h=L1sinθ1+R-Rcosθ1

(3)

(4)

x=L1cosθ1+R-Rsinθ1

(5)

(6)

(7)

攀爬高度模型如下所示：

(8)

机器人爬高台阶时攀爬台阶的高度由中间摆臂与前摆臂履带的有效半径决定,攀爬高台阶过程如图6所示。

图6 机器人攀爬高台阶示意图

同攀爬低台阶的分析过程一样,攀爬高度h、有效半径Re与履带夹角θ1,θ2的关系式如下所示：

h(θ1,θ2)=Lsinθ2+L1sin(θ2+θ1)+R-Rcosθ2

(9)

x=Lcosθ2+L1cos(θ2+θ1)+R-Rsinθ2

(10)

Re(θ1,θ2)=

(11)

攀爬高度模型如下所示：

(12)

1.5 翻越台阶运动学建模

机器人质心位置随着摆臂履带与中间履带夹角的变化而变化;机器人能够翻越台阶的条件是机器人的质心能够运动到台阶侧臂面,实现成功翻越[9-10],如图7所示。以后摆臂轮圆心为坐标系XOY的坐标原点,水平方向为X方向,竖直方向为Y方向,机器人质心与履带夹角动态变化关系如下所示：

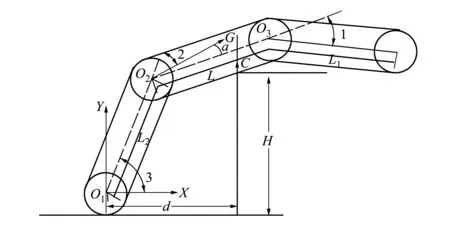
图7 机器人翻越台阶示意图

(13)

后摆臂轮圆心O1到台阶的距离为d,当达到翻越台阶的临界条件时,XC=d,此时,翻越台阶高度

H=L2sinθ3+

(14)

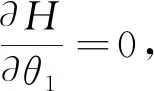
机器人翻越高度模型如下

(15)

1.6 机器人爬台阶求解

该水陆两栖机器人的结构参数如表1所示。

表1 机器人结构参数

机器人攀爬低台阶时,台阶高度h、摆臂履带有效半径Re随摆臂履带夹角θ1变化曲线如图8所示;攀爬高台阶时,台阶高度h、摆臂有效半径Re随摆臂履带夹角θ1,θ2的变化关系曲面如图9所示;机器人翻越高度H随摆臂履带夹角θ1,θ3变化曲面如图10所示。

图8 低台阶下攀爬高度与有效半径曲线 图9 高台阶下攀爬高度与有效半径曲线图10 机器人翻越高度曲面

对上节建立的机器人越障模型进行求解。对于低台阶,当θ1=35.3°时,机器人具有攀爬最大高度hmax=157.9 mm;对于高台阶,当θ1=-0.39°时,θ2=45.1°时,机器人具有攀爬最大高度hmax=467.5 mm。

对于机器人翻越高度,当θ1=-48.9°,θ3=94°时,机器人具有翻越最大高度Hmax=354.3 mm。

考虑机器人爬台阶必须同时满足攀爬和翻越条件,因此,机器人能够爬行台阶的最大高度为354.3 mm,高度小于157.9 mm时,以第一种规划步态爬台阶以提高爬行效率,高度大于157.9 mm时以第二种步态爬行以发挥最大爬行能力。

1.7 机器人爬台阶步态验证

选取低台阶高度为150 mm,采用低台阶规划步态进行机器人爬低台阶过程验证,如图11所示,对应于图3中b)～e)过程,机器人在爬低台阶时按照规划的步态能够快速高效越过高台阶;

选取高台阶高度为350 mm,采用高台阶规划步态进行机器人爬台阶过程验证,如图12所示,对应于图4中3～8过程,机器人爬高台阶时按照规划的步态进行高台阶攀爬和翻越,能发挥更大爬台阶能力。

图12 机器人爬高台阶规划步态验证

2 陆地行进间强瞬态冲击稳定性分析

在机器人运载平台上装有三自由度机械臂,即l1绕z1轴的旋转运动,l2绕l1和l3绕l2俯仰运动,如图13所示。机器人行进间强瞬态冲击的稳定性不仅受自身结构影响,还与机械臂的各关节角有关,F为强瞬态冲击力,作用于l3,GC作用在机器人对称面上,假设机器人以速度v匀速向前运动,且始终保持牵引力与地面对机器人摩擦力平衡。

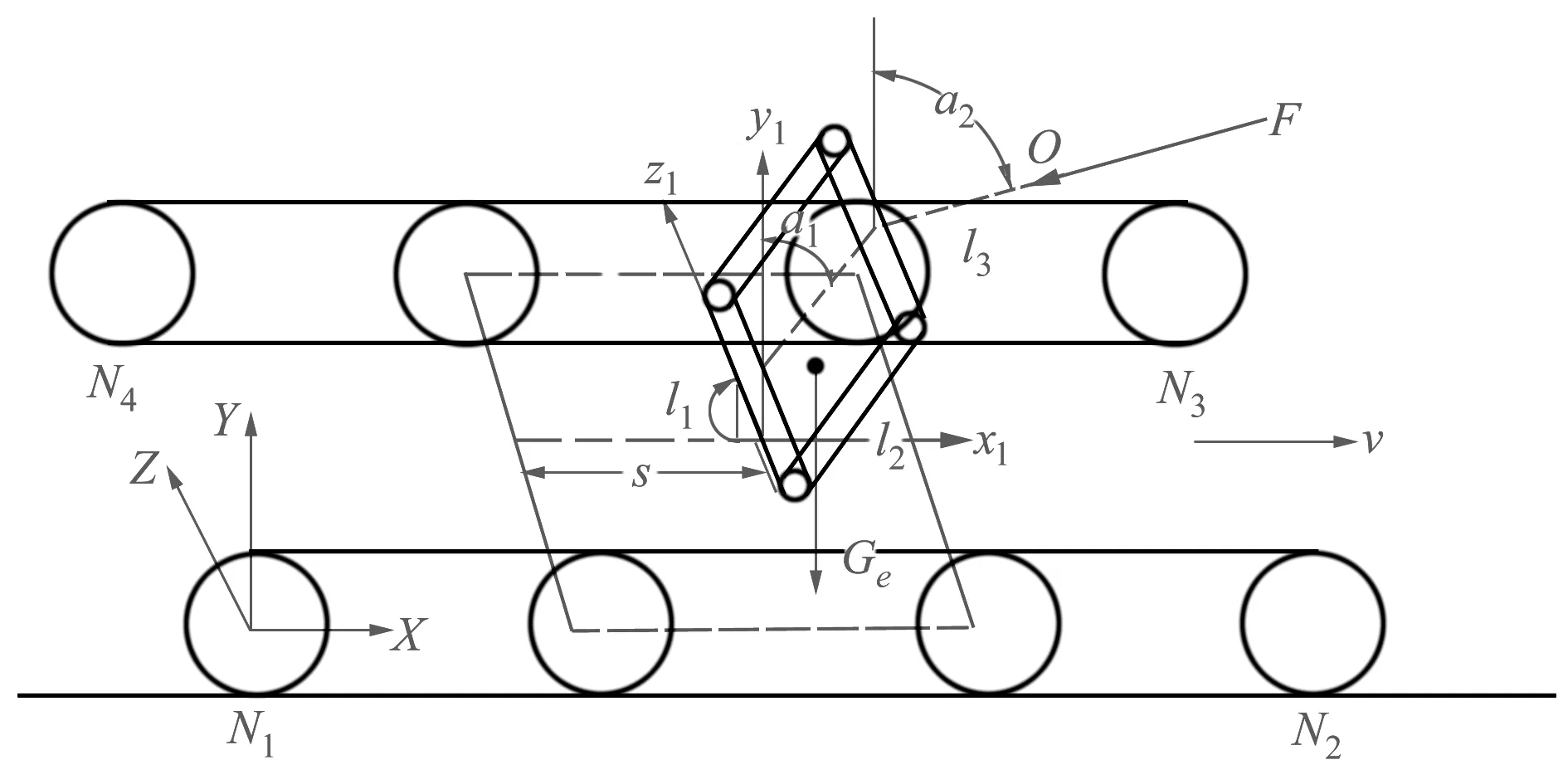
图13 行进间武器发射示意图

机器人在行进间受强瞬态冲击时,产生的不稳定性主要有发生倾倒、侧向滑移、正向后退,其中发生倾倒的情况有四种,分别绕N1N2、N3N4、N1N4、N2N3倾倒。为保证机器人受强瞬态冲击不发生倾倒,需满足以下条件

机器人行进间受强瞬态冲击还要保证侧向不发生滑移,正向不后退,因此,需满足以下条件

|uz(Fcosα2+GC)|>|Fsinα2sinφ|

(19)

(M+m1+m2)v>(Fsinα2cosφ+uXFcosα2)t

(20)

式中：F为强瞬态冲击力；uX,uZ为机器人在坐标系XYZ中X方向与Z方向的摩擦因数；α1,α2为机械臂关节与y1方向的夹角；φ为l3在x1z1平面上的投影与x1方向夹角；(x1,y1,z1)为o点在x1y1z1坐标系的坐标。

其中

该机器人平台上的机械臂主要搭载武器发射系统,行进间的强瞬态冲击主要为武器发射的瞬时后坐力,以上机器人行进间强瞬态冲击稳定性判别条件,只与机械臂位置角(α1,α2,φ)有关,因此,在机器人平台上的武器发射之前,通过姿态传感器获得各机械臂位置角(α1,α2,φ)进行稳定性预判,通过不断调整机械臂姿态角以确保武器发射时的机器人稳定,为机器人的机械臂关节电机控制提供理论基础。

3 水中行驶阻力及压力分析

机器人水中行驶阻力、压力与行驶速度有关,并影响水中行驶的快速性,由于表面具有较高的方形系数,周围的黏性绕流场分离较大,水面行驶兴起于喷溅的波浪较大[11],使得数学计算水动力难度较大,因此,采用Fluent对两栖机器人的水动力学特性进行数值仿真与分析,主要研究机器人的水中摆臂履带伸开、收缩状态下的行驶阻力,以及行驶阻力与行驶速度关系,为机器人水中行驶摆臂状态选择和行驶速度的设定提供数据源支撑。

3.1 数值模拟

1) 模型选择与假设

RNG(重整化群)k-ε模型考虑到旋转效应,相对于标准k-ε模型具有更好的计算精度,其湍动能k和耗散率ε方程为

两栖机器人水面绕流是两相流动问题,自由液面为水和空气的交界面。VOF(流动体积法)通过控制网格单元被流体填充的比例函数来实现水气交界面的追踪。水气两相流中,水的体积分数αw和空气的体积分数αa应满足如下关系

αw+αa=1

(23)

当αw=0时表示流体全为空气,αw=1时表示流体全为水,0<αw<1表示流体为水、空气两相。

水、空气两相流相对于单相流的连续方程、动量守恒方程、k-ε方程同样适用,只是方程中的密度系数ρ、动力黏度系数μ是由水、空气两相共同决定的,其水、空气混合相的密度系数ρ、动力黏度系数μ为

(24)

ρw,ρa为水、空气的密度系数,μw,μa为水、空气的动力学黏度系数,在温度为288 K,标准大气压下水密度为1 000 kg/m3,动力黏度系数为0.001 003,空气为不可压缩理想气体。

为了简化模拟计算,假设机器人在水面行驶时只有前进一个自由度处于正浮状态,不考虑机器人水中的垂荡和纵摇,且水面为风平浪静水面,不考虑水浪现象。

2) 边界条件

常见的入口边界条件有速度入口、质量入口、压力入口,该流体数值仿真的入口条件为速度入口,由于机器人水中行驶速度较低,默认空气为不可压缩气体;出口边界为自由出口,即水自由流出,且出口边界距车尾长度应尽可能大,以减少出口流体回流产生的影响[12]。考虑流体黏性的影响,设侧壁面为无滑移壁面,底部壁面为滑移壁面以模拟河床的运动,车体表面为无滑移壁面。边界条件如图14所示。

图14 边界条件

3) 网格划分

为了提高网格质量和计算效率,对机器人履带进行了简化,如图15所示,分别为机器人水中行驶时摆臂履带伸开和收缩状态,伸开状态使机器人水线变长,收缩状态使机器人整体更为紧凑。

图15 机器人简化模型

流体数值计算中划分的网格质量和数量对计算精度、效率、稳定性都有很大影响,为了使计算有高的精度与效率,针对计算区域的不同结构特点,采用结构网格与非结构网格混合的混合网格[12-13]。对于远离车体的流场区域等简单有规则结构,采用结构网格(六面体网格)以减少网格数量,提高计算效率;对复杂结构的两栖机器人车体采用适应性强的非结构网格(四面体网格),对于两栖机器人的履带等复杂结构加密网格以捕捉重要的边界信息,自由表面处需细化网格,以较准确模拟流体波和兴波现象。计算域网格如图16所示。

图16 计算域网格划分

4) 数值求解

求解方法选择SIMPLE算法进行压力和速度耦合,体积分数、湍动能、耗散率采用一阶迎风差分格式,动量和能量采用二阶迎风差分格式。求解过程中松弛因子大小影响求解的稳定性和收敛性,小的松弛因子使得每次迭代间的变化量也较小,收敛速度较慢,但收敛效果较好,经过反复选取收敛因子结果比较,设置压力、动量、湍动能k、耗散率ε的松弛因子为0.1,0.2,0.2,0.2。

3.2 摆臂履带伸开与收缩状态下水气分布

在水速为3 m/s、空气流速为5 m/s条件下的车体表面水气分布如图17所示,

图17 机器人表面水气分布图

由水气分布图17知,履带伸开状态下机器人表面周围的水浪分布较为均匀,履带收缩状态下机器人表面水浪分布呈现前高后底的状态,这是由于履带伸开状态下,机器人前部产生的水浪被前摆臂履带轮抵挡一部分,而履带收缩时,机器人前部的水浪能够顺利地向后散去,这会表现在车体阻力的减少。从以上水气分布结果可以看出,仿真能够很好地模拟两栖机器人水中的真实情况。

3.3 摆臂履带伸开与收缩状态下表面压力分析

机器人水中行驶时表面上总压力由静压与动压构成,其中静压就是平常所说压力,而动压是由流体的速度和密度特性决定的,具体为p=0.5ρv2。

机器人在水速为3 m/s,空气速度为5 m/s的流域内行驶稳定态的总压力分布如图18所示。

图18 机器人表面总压力分布

表2为机器人摆臂伸开与收缩状态下的压力比较,可知,机器人履带收缩状态下的局部最高压大于履带伸开状态下的局部最高压,而局部最低压近似相等,履带收缩状态下的平均压力低于履带伸开状态下的平均压力,这从侧面反映出机器人水中行驶时收缩前后履带会使机器人具有更小的行驶阻力。

表2 摆臂不同状态水中行驶压力

图19是机器人履带伸开和收缩状态下车体前部流域纵剖面流线图,可以看出,履带伸开时,水会在前摆臂履带与机器人前部包围的流域内堆积,不利于水的流动,这会导致机器人前部与前摆臂轮区域作用的压力较大,最终导致较大的行驶阻力;而履带收缩的状态下,由于水能够较轻易从机器人侧部流动,总体的行驶阻力也会较少。

图19 机器人前部流域纵剖面流线图

3.4 行驶阻力与行驶速度关系

在风速5 m/s条件下,不同水速时,机器人摆臂履带伸开和收缩状态下水中行驶阻力对比如表所示,水速为0表示机器人静止在水中,但由于风速的存在,仍有微小的阻力。

表3 不同速度下的行驶阻力

图20为机器人水中行驶时摆臂履带伸开与收缩状态不同行驶速度下的行驶阻力曲线图,可知,摆臂履带伸开状态下机器人行驶阻力明显大于摆臂履带收缩状态下的行驶阻力,且行驶速度越大,行驶阻力差别越大.

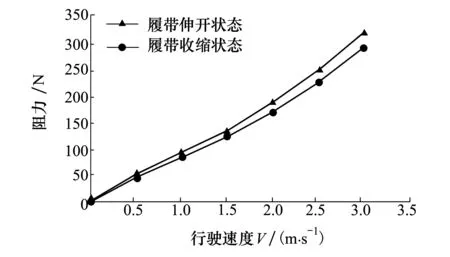
图20 机器人行驶阻力曲线

文献[13-14]对两栖车水中行驶阻力与速度关系进行了研究,得出两栖车水中行驶时总阻力与行驶速度为幂次关系;因此假设机器人在风速5 m/s时,行驶方向的总阻力Ff与水速v满足如下关系

Ff=k·vn+C

(25)

式中：C表示机器人在水中静止,5 m/s的风速引起的总阻力；n表示总阻力与水速的幂次关系。因此,可得机器人在5 m/s的风速下,行驶阻力与速度关系为

(26)

以上分析可知,机器人水中行驶时,摆臂履带收缩状态相比于摆臂履带伸开状态能够减少10%左右的水中行驶阻力,且在机器人的表面平均压强也更小,因此,当机器人从陆地转入水中行驶时应收起摆臂履带以减少水中行驶的阻力及表面平均压强。从机器人水中行驶阻力与行驶速度关系知,机器人水中行驶摆臂伸开状态相比于摆臂履带收缩状态下的行驶阻力受行驶速度的影响更大。

4 结 论

对所设计的水陆两栖运载机器人陆地上进行了2种爬台阶步态规划,基于规划的步态进行了爬台阶运动学分析,然后基于动力学理论对机器人行进间武器发射时稳定性进行了分析,最后基于流体数值模拟方法对机器人水中运动阻力、压力进行了分析。以上工作得出如下结论：

1) 本设计机器人爬台阶的最大高度为354.3 mm,当台阶高度小于157.9 mm,机器人以第一种规划步态爬行台阶以提高爬行效率,台阶高度大于157.9 mm时,以第二种规划的步态爬行台阶以发挥最大爬行能力;

2) 机器人行进间受强瞬态冲击稳定性与机械臂位置角(α1,α2,φ)有关,可通过控制机械臂的位置角(α1,α2,φ)来保证自身的稳定性;

3) 机器人水中行驶时摆臂履带收缩状态相比摆臂履带伸开状态下的表面平均压力更小,其行驶阻力减小幅度5%～11%之间,行驶阻力与速度关系如下。