基于直方图滤波的浅海声源测距算法研究

刘丽丽, 李京华, 冯晓毅, 石海杰, 张晓彪

(西北工业大学 电子信息学院, 陕西 西安 710072)

水下运动目标的测距一直以来都是水声学的研究热点问题,针对水下实现浅海声源的测距问题[1]。近年来许多研究者利用滤波技术来实现对浅海声源的跟踪及定位[2],郭晓乐等[3]提出了一种利用集合卡尔曼滤波算法的声速剖面跟踪反演和移动声源跟踪定位的方法,实现对声源的跟踪定位。高飞等[4]基于单水听器多途声到达时差,利用扩展卡尔曼滤波算法对深海浅层移动声源进行定位研究,以首达波与次达波的声到达时差为观测值,构建EKF声源定位模型,得到移动声源的深度、水平距离及速度等信息。上述算法都属于线性高斯目标的状态估计问题。而对于处理非线性非高斯目标的状态估计问题,本文提出了利用直方图滤波来实现对浅海运动声源的定位。首先,在统计模拟方法的基础上利用简正波建模方法对声源在水下声传播进行建模仿真,对由多个环境变量引起的传播损失进行分析,捕捉环境因素的不确定性；其次研究了统计模拟方法模型产生的声场预测集合的统计特性,采用概率密度估计方法对声场在不同水平距离-深度处的幅度分布进行了分析实验,得出在不同水平距离-深度上声压幅度的概率密度分布;最后,利用对声场模型的概率估计结果以及接收信号等先验知识利用直方图滤波实现对声源的距离估计,并利用实测数据进行实验以验证算法有效性。

1 基于统计模拟方法的声场建模

为了验证本文测距算法的有效性,本文的仿真实验采用SwellEx-96[5]实验中的S5事件的海洋环境参数[6]。海洋环境参数如图1所示。

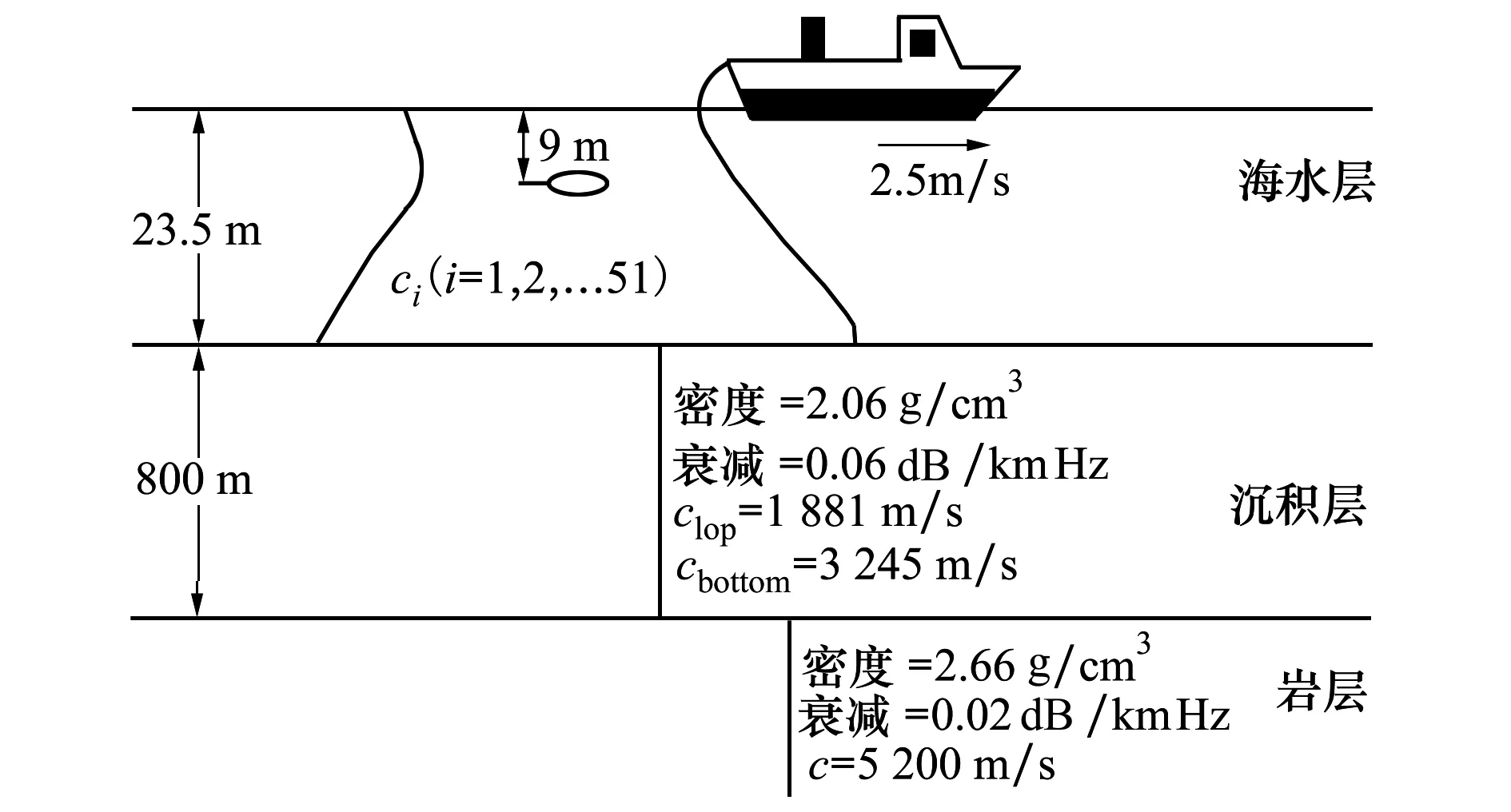
图1 SwellEx-96实验海洋环境参数示意图

在图1中,最上面是水层;水层下方为沉积层;沉积层下方是岩层。在SwellEx-96实验周围海域中,在不同的时间段内进行了51次声速剖面测量,测量结果如图2所示。

图2 SwellEx-96实验期间测量的51次声速剖面示意图

如果确切地知道声速剖面,海水深度和沉积物特征,就可以得到单一环境参数的声场。然而在实际应用中,建模用的环境参数存在着不确定性,选择不确定的参数值将导致建模的声场与实际接收的声场数据之间存在较大的差异。因此,为了分析环境参数的不确定性对声场建模产生的影响,本文在单一环境参数简正波建模的基础上,使用统计模拟方法进行声场建模,用SwellEx-96的51种声速剖面以及不同接收器深度的环境参数条件进行多环境参数建模,从而得到不同环境参数下的声场模型。

首先,利用简正波模型实现单一环境参数下的声场建模,声源强度S在深度zs处的声场p(r,z,t,zs)为[7]

(1)

式中,am(Km)是第m阶简正波的水平波数的模式激励,(1)式表示简正波建模产生的声场是m阶不同简正波模式的叠加。依赖声速曲线和第m阶简正波的激发系数Zm(zs),可得到声场的形式为

(2)

单一环境参数建模时声速剖面选取51组声速剖面的第一组。图3所示为频率109 Hz的浅海声源在水下9 m处的声场传播衰减图。可以看出,声源在正下方的传播衰减最小,传播过程中随着水平距离和海水深度的增大,传播衰减也逐渐增大。这是因为海底泥沙等引起的声反射对其传播所产生的干扰所导致。

图3 浅海9 m处声源的传播衰减图(分贝)

其次,进行多环境参数下的简正波建模,设影响声场建模的环境参数为se,使用联合概率密度f(se)表示参数的不确定性。采用统计模拟方法从f(se)中随机抽取环境参数,实现声场建模。利用不同的环境参数重复该过程M次,则得到多种环境参数的声场集合,如表1所示。

表1 基于统计模拟方法的声场建模算法描述

统计模拟方法描述了不同位置处的声压值集合f(p|r,z),声传播过程可以看作是从环境参数到接收信号声压的映射p(r,z,se),表示为

(3)

若环境参数中有一个是变化的,则声场的变化也取决于该参数的变化,设环境参数的先验信息表示为

(4)

式中：μ为均值；σ2为方差；η表示幅度；f(se)表示关于环境参数的先验信息,联立(3)至(4)式得

f(p|r,z)=

(5)

本文针对同一个目标声源,分析了声速剖面和水听器深度变化对建模的影响,其中,声速剖面为图2中51组声速剖面曲线,水听器深度从80～100 m深度范围(步长为1)变化,使用枚举法对声速剖面和水听器深度的1 071(51×21)种组合进行声场仿真,结果如图4所示,得到不同海洋环境参数下声场的集合。

图4 统计模拟方法下的简正波声学建模结果示意图

2 基于概率密度估计的接收信号仿真

2.1 水下接收信号模型

水听器接收声源信号的示意图如图5所示。其中水下声源为黑色椭圆,水听器为黑色圆点。声源到水听器的水平距离为r[n],声源深度为z[n]。声源辐射的信号记为a[n],接收的信号记为x[n],n是离散时间,声源接触到海底会发生反射,声信号的传播方向用带箭头的直线表示。

图5 水听器接收声源信号的示意图

由声源辐射的信号a[n]表示为

a[n]=ASL[n]cos(2πf0+θ)

(6)

式中：ASL[n]是声源幅度;f0是声源信号的频率;θ是相位。

当信号在浅水环境中传播时,与底部和表面接触多次,从而导致多径传播现象[8],因此,声信号传播到水听器会发生一些变化。单个水听器上接收到的声源信号x[n]表示为

x[n]=A(s[n])cos(2πfdn+φ)+W[n]

(7)

式中：W[n]是噪声;fd是多普勒频移[9];A(s[n])是接收信号幅度;s[n]是声源位置的函数,称为声源状态向量,它取决于声源的水平距离、深度、径向速度和幅度。

(7)式中的接收信号幅度A(s[n])可以分解为声源幅度ASL[n],以及由传播过程产生的幅度c[n],即不同水平距离-深度处信号的幅度变化,表示为

A(s[n])=ASL[n]c[n]

(8)

如果准确地知道环境参数se,那么就可精确得到由声传播引起的幅度衰减c[n]。但实际情况由于环境参数是变化的,因此,本文在统计模拟方法建模的基础上,用概率密度估计方法计算出由环境参数引起的c[n]幅度值的变化,得到不同时刻(即不同水平距离-深度处)的幅度分布,由(7)、(8)式计算得出接收信号x[n]。

2.2 概率密度估计方法原理及仿真

采用密度估计方法对不同水平距离-深度处的幅度变化进行概率密度分布估计,从而实现接收信号的建模。

(9)

式中：ω(p-pi;h)是核函数;h为核宽度,核函数可以是任意的形式,这里定义是高斯核函数,表示为

(10)

(11)

进一步可简化为

(12)

式中

(13)

(14)

联立(13)式和(14)式可将(12)式简化为

(15)

(15)式不是直接适用的,因为需要基础概率密度函数f(p)的真实形式,本文中的f(p)为高斯核密度形式,因此,(15)式可以进一步简化为

(16)

σ是基础概率密度函数f(p)的标准差。

采用核密度估计的方法对声源在水下传播时声压随距离衰减情况进行统计,得到接收信号幅度在不同水平距离-深度处的幅度衰减,其统计过程示意图如图6所示。图6a)为统计模拟方法产生的声场集合,图6b)为对声场集合中所有红色方块(表示水平距离-深度单元格)中声压幅度值统计的概率分布直方图,是对声场集合中1 071个传播损失图中每一个红色方块进行声压幅度的统计,其中红色方块的取值范围是水平距离20 m,深度4 m。

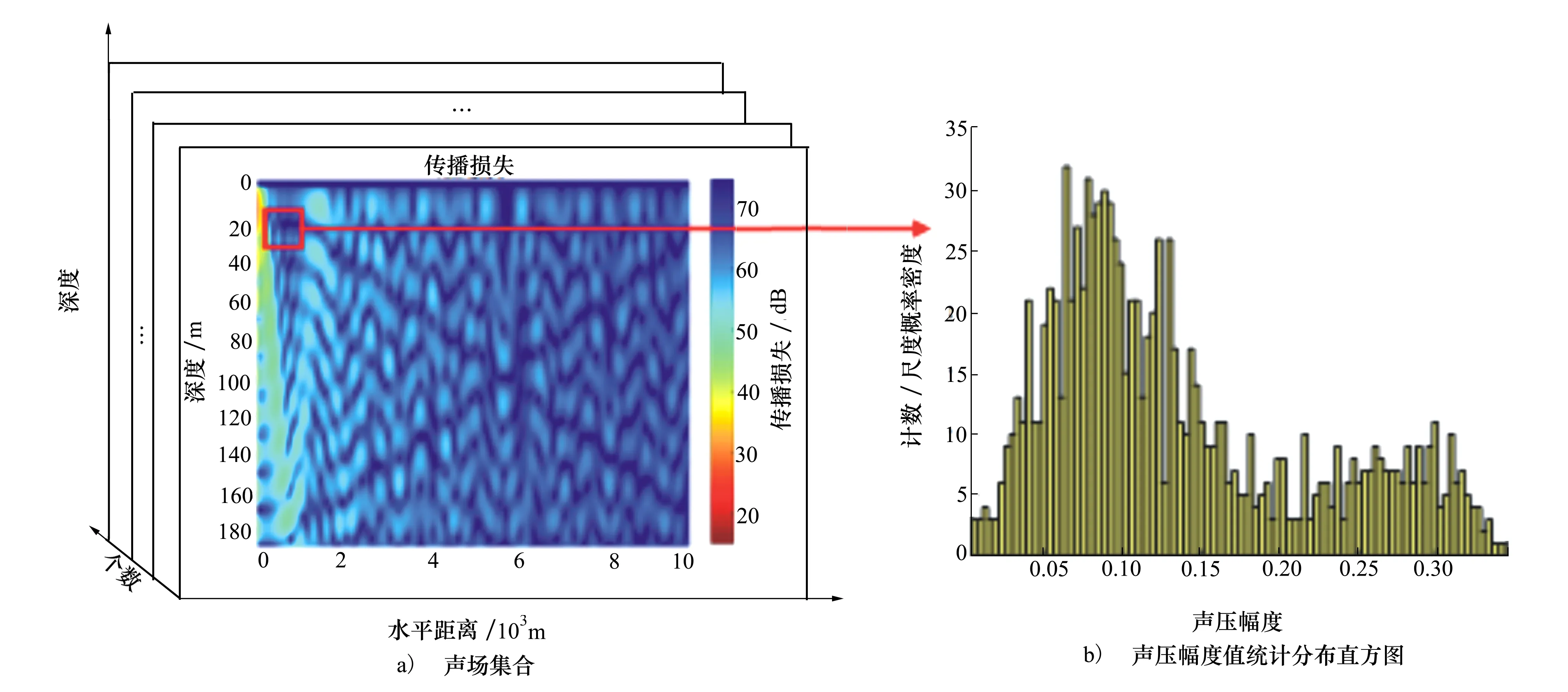
图6 某水平距离-深度位置处的声压幅度直方图

图7为对频率109 Hz浅海声源的声场建模结果采用核密度估计的结果。由图7可以看出核密度估计得出的概率密度函数与直方图有很好的对应关系,对数据的拟合较好,因此选择核密度方法实现声源对声源在不同位置处的幅度衰减估计,从而实现接收信号的仿真。

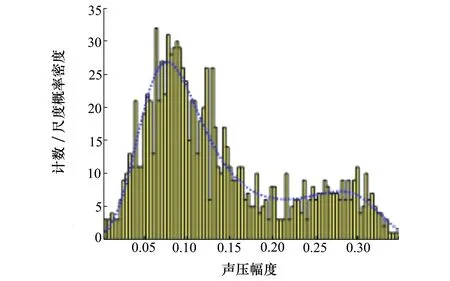
图7 核密度估计结果示意图

图8为仿真接收信号与实测接收信号的时域与频域波形对比图,仿真接收信号时采用了与SwellEx-96海洋环境相同的参数,实际接收信号数据则是来自SwellEx-96水平线阵HLA South中的一个水听器1在10～13 min时间段所接收的数据。

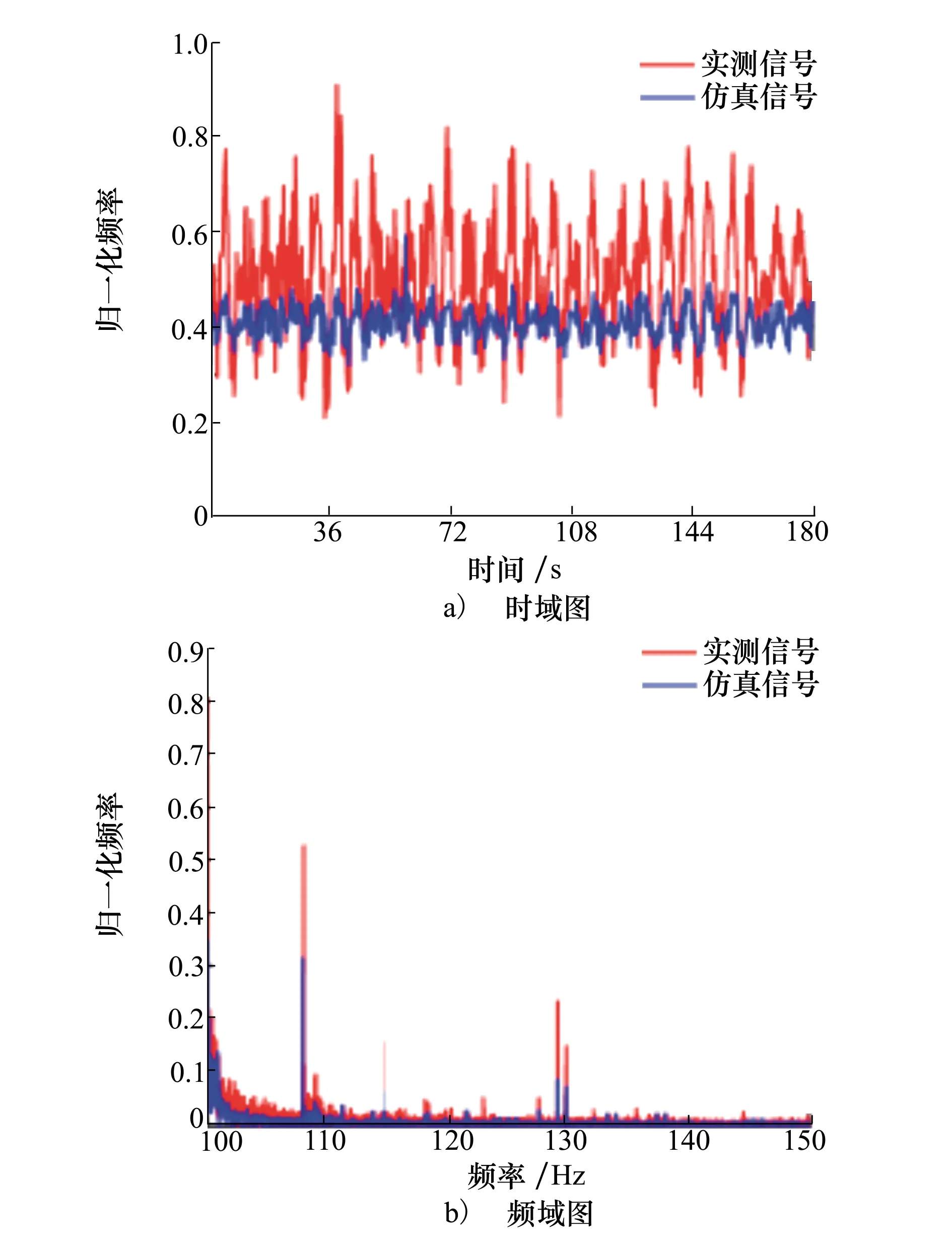
图8 实测接收信号与仿真接收信号时域与频域波形对比图

由图8可知,仿真的接收信号与实测接收信号之间除了存在幅度上的差异之外,时域波形起伏、频谱分布等都很类似,因此表明仿真的接收信号是有效的,这里在原数据的基础上进行了隔点采样,采样频率降为5 000 Hz。

3 基于直方图滤波的浅海声源测距

3.1 直方图滤波算法原理

直方图滤波[11]是Bayes滤波[12]的一种基于网格的实现,将状态空间分解成多个有限区域,划分后利用直方图滤波算法计算状态向量,它给出状态向量在每一个区域的概率,区域划分越精细计算结果就越精确,本文将水平距离、深度划分为20 m,4 m的区间,结合目标的先验知识和状态更新方程,利用直方图进行逼近,实现对声源的测距。

与大多数滤波器一样,直方图滤波也包含预测和更新两步,下面将进行分析说明:

当声源信号在水中传播时,产生的压力波动由一个水听器接收,水听器所接收的信号包含关于声源位置和幅度的信息。

利用声源运动参数和新的接收信号,可以在每个时间步长更新状态向量,用后验概率密度函数表示为f(sk[n]|x[1],…,x[n])。在前一时刻直方图滤波的输出表示为f(sk[n-1]|x[1],…,x[n-1]),使用直方图滤波将其更新为当前时刻的输出表示为

f(sk[n]|x[1],…,x[n])=ηf(x[n]|sk[n])×

f(sj[n-1]|x[1],…,x[n-1])

(17)

式中，f(sj[n-1]|x[1,…,x[n-1]])表示直方图滤波在n-1时刻产生的状态向量,状态向量s[n]由4个声源参数组成,包括声源到接收器的水平距离、深度、速度和幅度。

f(sk[n]|sj[n-1])称为状态更新方程。对于具有K个可能值的状态向量,f(sk[n]|sj[n-1])具有K2个可能性,因为对于j和k都有j,k=1,2,…,K。因此,若状态向量在时间n-1处的第j个值已知,则该状态在时间n处的第k个值的概率由f(sk[n]|sj[n-1]得出。状态更新方程是一个概率密度函数,表示关于状态向量值如何随时间变化的先验知识,如(18)式所示

(18)

式中：m为均值向量;Σ为协方差矩阵,m表示为

m=[μr,μv,μz,μSL]T

(19)

式中,下标r,v,z,SL分别表示声源的水平距离、速度、深度以及幅度。

因为状态向量是独立更新的,所以协方差矩阵Σ表示为

(20)

(17)式Σf(sk[n]|sj[n-1])f(sj[n-1]|x[1],…,x[n-1])是状态向量的总和,使用卷积来计算。在更新过程中,状态向量f(sj[n-1]|x[1],…,x[n-1])通过与状态更新方程进行卷积,得到的是不同的概率值,表示在已知n-1时刻所有数据的情况下,在时刻每个状态向量值分布的可能性。

(17)式中的f(x[n]|sk[n])是对声学建模结果用核密度方法估计的结果。η是确保(21)式输出的是有效的概率函数

(21)

总体来说,(17)式表示的是直方图滤波一次状态更新的结果f(sk[n]|x[n]),它描述了单个接收信号的状态向量sk[n]在时间n时的可能性。此时,后验概率密度f(sk[n]|x[n])比单个接收信号吸收了更多的信息,因为直方图滤波还使用状态向量先验概率密度函数f(sj[n-1])、状态更新方程f(sk[n]|sj[n-1])和描述声场的概率密度函数f(x[n]|sk[n])。比起贝叶斯滤波器,直方图实现起来容易得多,因为积分已被求和取代,非常适合在计算机上进行数值计算。

上述介绍了直方图滤波的状态更新过程,它的更新是递归的,因此前一次更新产生的后验概率密度函数是后一次更新的先验,直方图滤波的算法描述如表2所示。

表2 直方图滤波测距算法描述

直方图滤波得出的是声源状态向量的后验概率密度,包括水平距离,深度,幅度和速度,可以将其任何一个进行边缘化[13],得到不同时间内对该参数的估计结果,边缘化深度、幅度和速度可表示为

f(r[n]|x[1],…,x[n])=

∬f(r[n],v[n],z[n],ASL[n]|x[1],…,x[n])

dASL[n]dv[n]dz[n]

(22)

类似地,也可以对其他参数进行边缘化。

总而言之,直方图滤波算法即使先验知识为非高斯、多模态、相关或非参数概率密度函数的形式,仍然可以实现。当了解状态向量的先验概率密度函数、状态更新、环境参数和声场导致状态向量后验的变化时,可以利用先验知识实现精确的测距。

3.2 仿真实验及结果分析

3.2.1 算法相关参数设置

仿真时,将声源的水平距离、深度、径向速度以及幅度作为状态向量,结合声源运动过程中接收到的声压值以及状态更新方程,在每个划分区域内根据前一时刻估计得到的声源状态向量,估计出当前时刻的声源状态信息。状态更新的目的是准确表示声源状态向量参数随时间变化的先验知识。其中状态向量的网格参数(状态空间)设置如表3所示,不同的步长表示不同的划分区间。

表3 状态向量网格参数

表4给出了实验过程中(18)式所示的状态更新方程的均值和协方差的数值。

表4 状态更新的参数

3.2.2 仿真结果

采用直方图滤波算法进行目标测距,接收信号频率为109Hz和127Hz,声源位于海平面下9m,沿水平方向匀速运动,速度为2.5m/s,声源运动时长为50min,水听器位于水下100m。图9为在不同时间段对109Hz声源的水平距离和深度的估计结果,其中127Hz声源实验结果也同理可得。

图9中每个图对应不同时间下的距离估计结果,声源的实际位置用红色O表示,声源的估计位置用红色X表示,灰度为概率密度的对数,灰色颜色越深表示目标在该位置处的可能性越大,反之则越小。因刚开始时先验知识较少,所以测距结果灰色分布范围较大,随着时间的增大,状态向量在不断更新,声源在真实位置的可能性比在其他位置的可能性变大,灰色颜色变深且越来越集中。

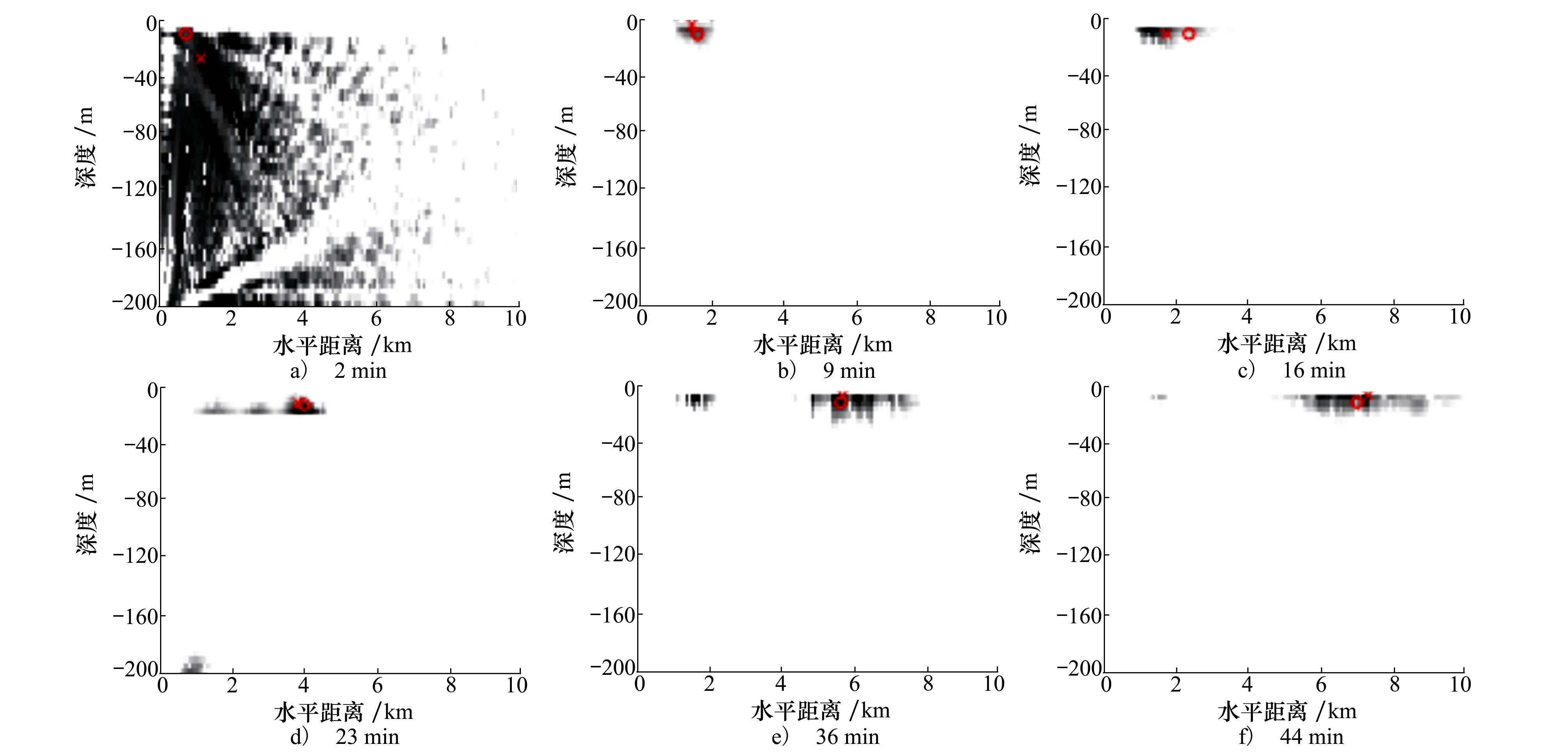
图9 浅海109 Hz声源的距离估计结果

图10为109Hz声源在边缘化其他3个参数(声源幅度、速度、深度)后在不同时间内对水平距离和深度的估计结果,灰色较深的区域表示目标最可能的位置,红线是实际声源水平距离和深度随时间的变化结果。图11为对109Hz声源的速度和幅度估计结果,红线是实际声源速度和幅度与时间的函数关系。图10至11是对声源状态向量的后验概率密度进行边缘化生成的,通过将每个参数的概率密度函数表示为时间的函数,可以清楚地看到随时间变化的参数估计结果。在刚开始时,状态向量参数存在明显的不确定性。这有2个原因:①先验概率密度函数是四维均匀分布的,排除掉不可能的状态向量参数需要一些信息,例如,一开始很难判断一个声源的幅度是接近一个较低的还是较高的幅度;②传播模型在很短的时间范围内往往是不准确的,随着测距算法状态向量参数的不断更新,状态向量参数的估计结果会提高。从图11b)可以看出对声源幅度估计的结果很准确,因此可以将声源幅度边缘化,从而观察声源速度对水平距离和深度估计结果的影响,绘制声源速度、水平距离以及深度的三维等概率轮廓。图12为对109Hz声源在第9分钟时状态向量的三维等概率面。可以看出,声源在第9分钟时,尽管声源速度有些不确定,但此时水平距离和深度几乎没有不确定性,表明了速度对于水平距离的估计影响较小,证明了距离估计的有效性。

图10 在不同时间下对声源水平距离和深度估计结果 图11 在不同时间下对声源速度和幅度估计结果

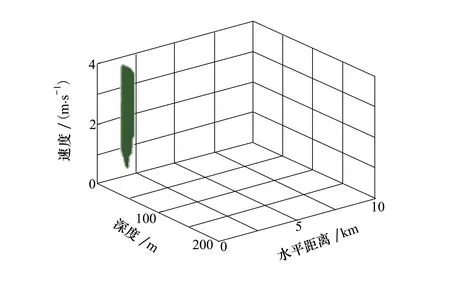
图12 声源在9分时的三维等概率面

下面将对测距的误差进行分析,通过选取不同的误差窗口大小,从而计算对声源距离估计结果的正确率。表5给出了在选取不同的误差窗口下对距离估计结果的正确率,其中水平距离和深度所取的误差分析窗口有所不同。

表5 不同误差窗口距离估计的正确率

由表5可以看出,对水平距离估计正确率比较好的情况是窗口大小为±10m左右,正确率达到90%左右;而深度估计正确率比较好的情况则是在±0.5m左右,正确率也达到90%左右。误差来源可能是对状态空间的区间划分以及状态更新方程的参数设定,理论上状态空间划分越小距离结果越精确,但随之会导致较大的计算量,本文在满足应用性的前提性选择了实验所设定的划分区间和参数。

图13为109Hz和127Hz频率声源在不同时间的距离估计结果与实际距离的偏差,计算公式如(23)式所示。

图13 距离估计结果误差示意图

(23)

图13可以看出不同时刻距离估计的偏差,此外，127Hz声源比109Hz声源的距离估计偏差更大,这是因为频率越高,声源传播的距离越短,因此在本文这种低频远距离的传播环境时,高频声源信号相比低频声源信号会产生更大一点的偏差。

在文献[14]中,采用匹配场方法在Swellex-96数据库测试得出定位结果水平距离误差除在个别时间内最大误差在0.5km左右,其他的都相对比较准确,本文在实验中估计的声源轨迹与GPS数据也比较吻合,误差也相对较小,因此本文对于浅海声源的水下测距是有效的,具有一定的参考意义。

4 结 论

本文针对海洋环境参数是时变的,提出了采用统计模拟的方法来捕捉海洋环境的不确定性,从而实现声场的建模,将环境不确定性映射为声场的不确定性,而并非某单一环境下的声场,使得建模结果更加接近真实的环境声场。为了对这一结果进行统计分析,得到传播损失在不同水平距离-深度处幅度的概率密度分布,采用了密度估计方法对该建模的结果进行估计,实现接收信号建模。最后提出了直方图滤波测距算法,它利用了统计模拟方法声学模型结果、接收信号数据以及声源运动参数等先验知识实现状态更新,实现对声源的距离估计,为实现水下声信号的处理提供了一定的基础。