永磁同步电机位置伺服系统的RBF神经网络滑模控制策略
汪圆萍,张俊,张兴
(安徽省电机产品及零部件质量监督检验中心, 安徽 宣城 242500)
0 引言
永磁同步电机(PMSM)具有高功率密度、高效率、高可靠性和动态响应速度快等优点,广泛应用于航空、机器人和机床等高速度高精度设备[1-2].然而,PMSM位置跟踪控制易受模型参数摄动、负载扰动和外界不确定性干扰的影响,导致控制精度降低,影响电机使用寿命,甚至给生产设备的安全稳定运行带来较大隐患[3-4].
工程上一般采用定子电流的q轴分量和常规PID控制方法来调节PMSM的转子位置[5],难以达到理想的调节效果.为此,国内外专家学者针对PMSM的转子位置控制提出了一些先进策略的研究方案.文献[6]针对PMSM外部负载扰动问题,在常规符号函数的基础上引入双极S型函数,一定程度上削弱了系统抖振,但由于系统不能保证在有限时间内收敛于原点,导致位置跟踪速度降低.文献[7]将PMSM的控制律设计为连续函数,将低通滤波器改进为反电动势观测器且增加了自适应结构算法,提高转子位置估算精度,但由于系统状态测量存在误差且缺少对误差的补偿,导致波形抖动较大.文献[8]针对PMSM控制过程中固定滑模增益导致鲁棒性差的问题,利用模糊控制设计模糊规则以整定滑模增益,进一步提高了系统的鲁棒性,但由于设计的模糊化和解模糊过程较为粗糙,导致PMSM位置控制调节时间过长,降低了系统响应速度.
为此,本文以PMSM转子位置为控制对象,提出了一种基于神经网络和滑模控制相结合的位置伺服优化控制策略,并引入干扰观测器实现对不匹配扰动的补偿.利用神经网络的自学习和自适应能力对滑模控制的切换增益进行及时调整以降低滑模控制系统的抖振,在此基础上,将提出的优化控制策略与常规PID和常规滑模控制进行MATLAB仿真对比来验证所提策略的优越性.
1 PMSM位置伺服系统构建
1.1 位置伺服系统动态特性分析在d,q旋转坐标系下,PMSM的状态方程为[9-10]:
(1)
其中:id为定子电流的d轴分量;iq为定子电流的q轴分量;ud为定子电压的d轴分量;uq为定子电压的q轴分量;Rs为定子电阻;L为定子电感;ψf为磁链;TL为电机的负载转矩;pn为极对数;B为粘性摩擦系数;J为转动惯量;w为角速度;θ为电机的角位移,即电机的转子位置.
取式(1)中的位置伺服系统:
(2)
令x1=θ,x2=w,则PMSM的数学模型可以用含扰动的动态状态方程来描述:
(3)
1.2 位置伺服系统控制方案设计针对 PMSM位置伺服控制系统的负载扰动、外部不确定性干扰和模型参数摄动的特点,本研究采用干扰观测器、神经网络和滑模控制器相结合的串级回路控制系统,整个控制方案如图1所示.图中,PMSM转子位置信号y通过位置变送器转换成4~20 mA的信号反馈至控制器输入端,该电信号与转子位置设定值θ*之间形成偏差信号e,RBF神经网络滑模控制器根据偏差信号输出的控制量iq作为副回路的设定值,副回路通过改变定子电流的q轴分量来调节PMSM的转子位置,并利用干扰观测器对电机扰动进行前馈补偿,从而提高PMSM位置伺服控制系统的稳定性.

图1 PMSM位置伺服控制系统整体方案
2 位置伺服系统控制器设计
2.1 滑模控制器的设计对于式(3)的PMSM数学模型,取切换函数为:
s=cx=[c11][x1x2]T=c1x1+x2
(4)
其中,常数c1应满足多项式λn-1+c1为Hurwitz,则:
(5)
iqeq=-(cB)-1[cAx+cBhd+chdd]
(6)
式(5)可表示成:
(7)
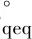
(8)
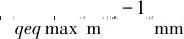
(9)
(10)
式中:K为滑模控制器的切换增益,K=(cB)-1σ.
假设cB>0,则
(11)
iq被确定后,系统状态轨迹将会在有限时间内到达滑模面,之后停留在滑模面滑动.滑模面上系统特征可以描述成:
(12)
从式(12)可以看出,滑模面上的系统不受电机的匹配扰动hd的影响,且
(13)
2.2 RBF神经网络滑模控制器设计系统状态轨迹在滑模面上的抖振主要是由滑模控制器的切换增益K引起的,且K越大,系统抖振越厉害.利用神经网络的自学习、自适应能力对切换增益进行调节,可有效降低控制系统的抖振[11-13].RBF神经网络滑模控制器的结构如图2所示.

图2 RBF神经网络滑模控制器
K=|wTz(q)|
(14)
式中:z(q)为高斯函数;w为RBF神经网络隐含层到输出层的连接权值.
(15)
式中:Ci为网络第i个节点的中心向量;ri为网络基宽向量中的第i个值.
定义目标函数:
(16)
式中:e为偏差,e=y-θ*.
神经网络连接权值的调整算法为:
(17)
式中:η为网络学习速率,η∈(0,1).

Δw≈-ηe(-1)sgn(s)z(q)sgn(wTz(q))
(18)
神经网络最终学习算法为:
w(t)=w(t-1)+Δw(t)+α(w(t)-w(t-1))
(19)
式中:α为网络惯性系数,α∈(0,1).
将神经网络的输出K值代入式(10),则控制律变为:
(20)
3 干扰观测器设计

(21)

为式(3)设计全阶比例积分观测器:
(22)

式(22)可表示成如下形式:
(23)

式(22)设计的全阶比例积分观测器的观测性能和存在性有如下引理:
4 仿真分析
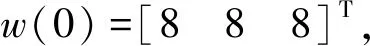
4.1 控制器相轨迹仿真对比系统的设定值θ*取幅值为1的正弦波信号,图3为常规滑模控制器的相轨迹,图4为干扰观测补偿的RBF神经网络滑模控制的相轨迹.

图3 常规滑模控制器相轨迹
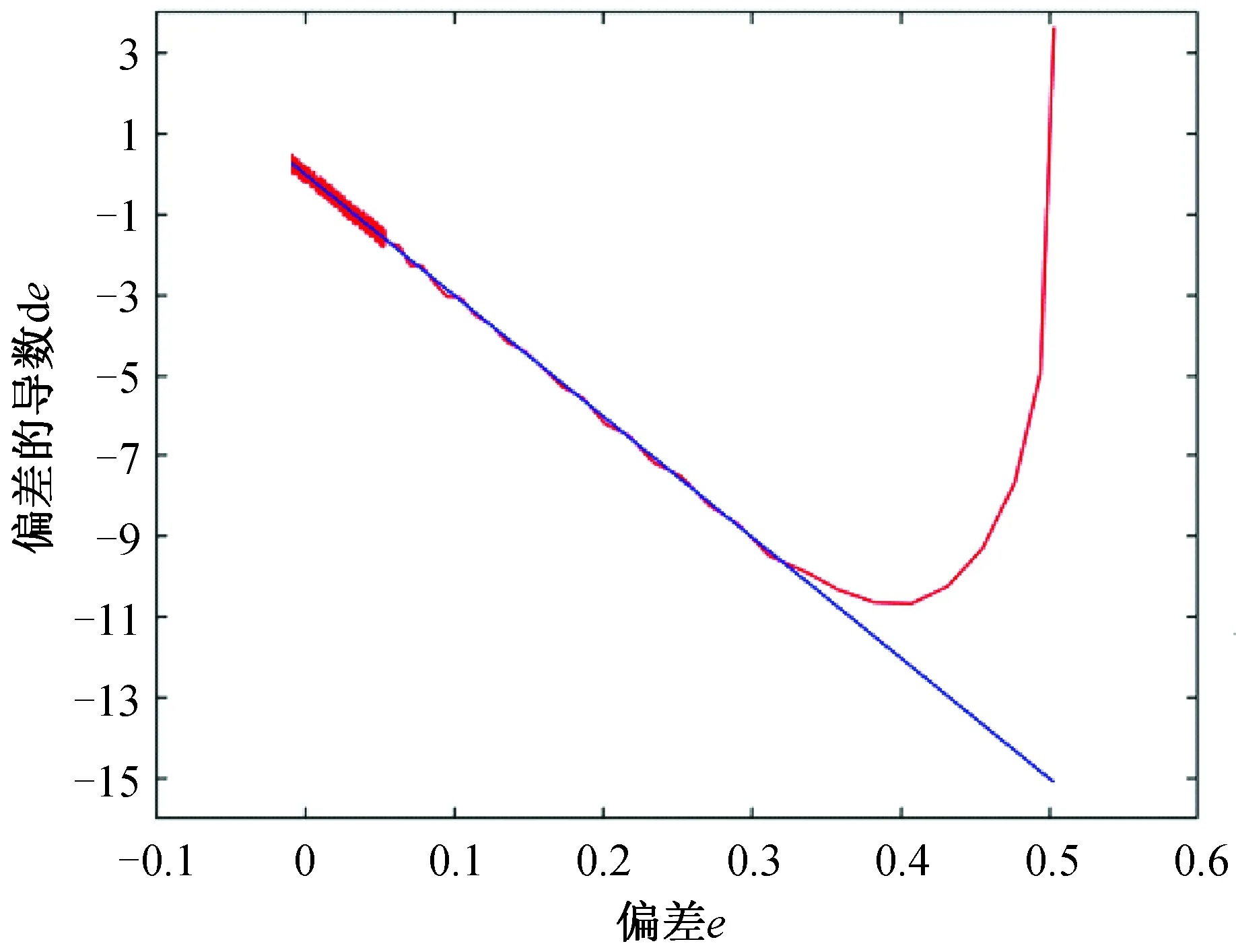
图4 干扰补偿神经滑模控制器相轨迹
对比图3和图4可知,常规滑模控制器相轨迹抖振明显,尤其在平衡点附近时抖振幅度达到了±0.4,波动较大.而RBF神经网络滑模控制器在平衡点附近时抖振幅度为±0.2,系统抖振幅度较常规滑模控制器降低了50%,说明神经网络对滑模控制的切换增益K具有良好的优化效果,能实时给出最优切换增益,降低系统抖振.
4.2 控制器位置跟踪仿真对比将系统的设定值θ*取2sin t的正弦波信号,图5和图6分别为采用常规滑模控制和干扰补偿神经滑模控制的跟随曲线和跟随误差.

图5 常规滑模控制跟随曲线及误差
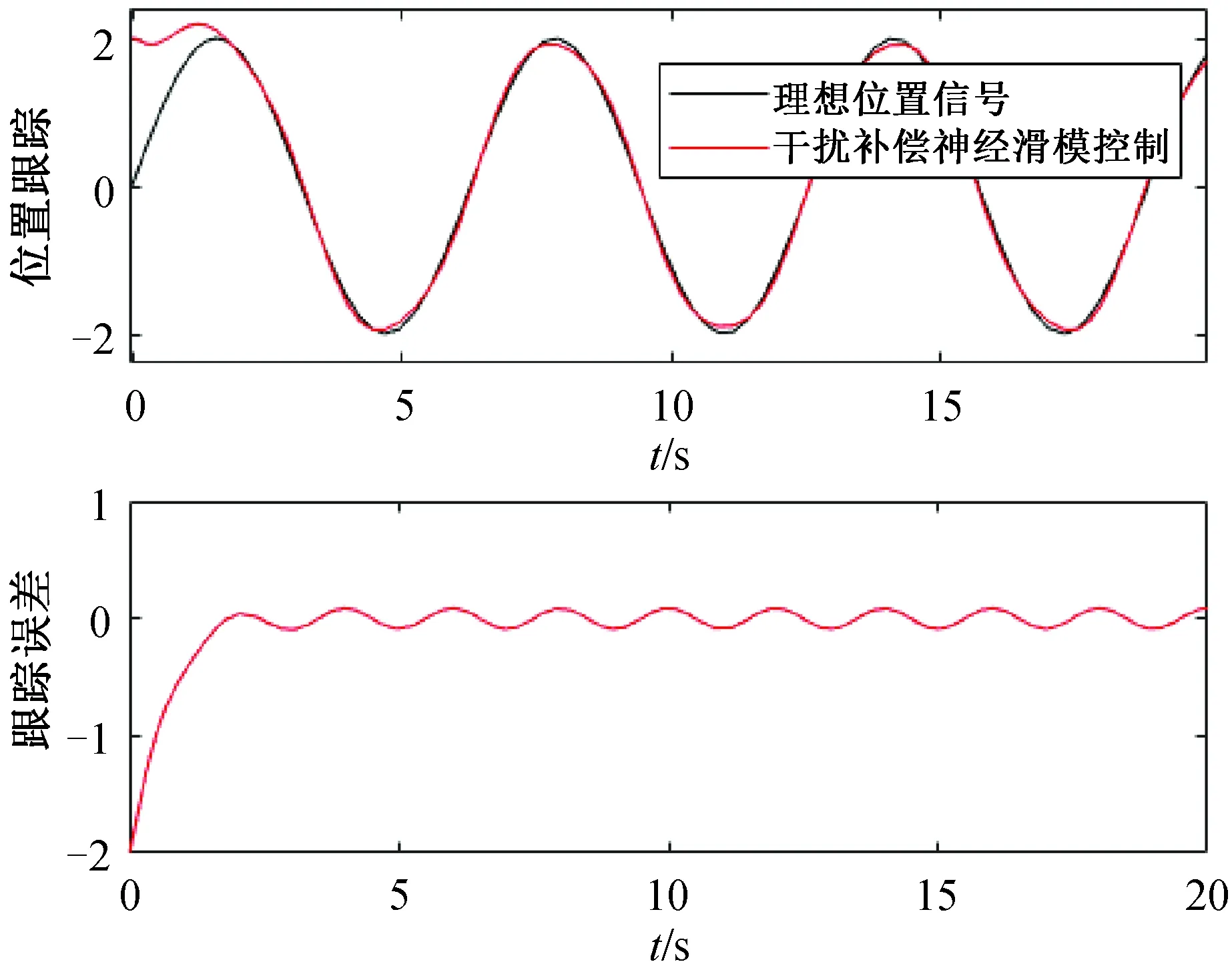
图6 干扰补偿神经滑模控制跟随曲线及误差
观察图5和图6可知,在同样的干扰信号下,采用常规滑模控制时的跟随误差在±0.5之间,而采用带干扰观测补偿的RBF神经网络滑模控制时的跟随误差在±0.1之间,系统跟随精度提高80%,优化后的控制策略的跟随性能得到较大提升.
4.3 控制器抗干扰性能仿真对比系统设定值θ*取单位阶跃信号,为验证优化控制策略的抗干扰效果,在系统运行到第22 s时加入幅值为25%的阶跃扰动信号,比较干扰补偿神经滑模控制策略、常规PID控制策略和常规滑模控制策略的抗干扰性能,其中,3种控制策略下阶跃扰动信号的时长均取2 s,仿真结果如图7所示.从图7可看出:扰动信号加入后,干扰补偿神经滑模控制策略的超调量为14.2%,调节时间为11.5 s;常规PID控制策略的超调量为27.9%,调节时间为16.8 s;常规滑模控制策略的超调量为22.7%,调节时间为15.8 s.由此可知,干扰补偿神经滑模控制策略的抗干扰能力明显优于常规PID控制策略和常规滑模控制策略.

图7 3种控制策略干扰仿真波形图
4.4 系统鲁棒性仿真本研究在PMSM模型参数精确仿真的基础上,对转动惯量J增大10%进行仿真以模拟参数摄动情况下优化控制策略的鲁棒性,如图8~9所示.从图8可以看出:在PMSM模型参数精确时采用干扰补偿神经滑模控制时的超调量为5.1%,调节时间为15.7 s;采用常规滑模控制时的超调量为15.3%,调节时间为16.1 s;采用常规PID控制时的超调量为21.5%,调节时间为23.4 s.从图9可以看出:在PMSM转动惯量参数发生摄动时采用干扰补偿神经滑模控制时的超调量为5.8%,调节时间为16.2 s;采用常规滑模控制时的超调量为18.9%,调节时间为16.8 s;采用常规PID控制时的超调量为27.8%,调节时间为25.4 s.相比常规PID控制和常规滑模控制,优化后控制策略在超调量方面的控制精度分别提高79.1%和69.3%,在调节时间方面的控制精度分别提高36.2%和25.6%。以上分析表明干扰补偿神经滑模控制策略在PMSM参数发生摄动情况下具有更强的鲁棒性.

图8 参数精确下的3种控制策略仿真波形

图9 参数摄动下的3种控制策略仿真波形
5 结论
本研究针对PMSM位置伺服控制系统,设计了带有干扰观测补偿的RBF神经网络滑模控制策略.利用神经网络自学习、自适应能力来调节滑模控制器的切换增益,有效降低了系统抖振,加入干扰观测器后的复合控制提高了系统的抗干扰能力.MATLAB仿真结果表明,所设计的控制策略抖振小,跟随性能好,在超调量和调节时间方面优于常规PID控制和常规滑模控制,具有更强的鲁棒性和抗干扰能力.

