角对称区域上二维不可压理想流体方程的稳态解

陈志豪，邓大文

(湘潭大学数学与计算科学学院， 湖南 湘潭 411105)

0 引言

本文中的角对称区域是指对应于极坐标中长方形区域的二维区域，包括全平面(r,θ)∈[0,∞)×[0,2π]，半平面[0,∞)×[0,π]，圆块0≤rR0等等. 本研究考虑两个二维理想流体方程组在角对称区域Ω上的稳态解，它们通常都是在直角坐标中给出. 第一个是二维不可压Euler方程组[1]

(1)

(2)

其中ur和uθ是速度场的径向和切向分量:u(r,θ,t)=ur(r,θ,t)er+uθ(r,θ,t)eθ，er=(cosθ,sinθ)，eθ=(-sinθ,cosθ)，ur，uθ，ω，ψ都是关于r,θ,t的标量函数.

又考虑半平面或平面上的无粘性无热传导性Boussinesq方程组[1]

(3)

(4)

其中,ω，ρ，ψ是关于r，θ，t的标量函数.

显式解一直是偏微分方程领域中的重要问题. 对不可压理想流体，经典工作都集中在二维和三维Euler方程的显式解，一些经典的结论和方法可参考Majda-Bertozzi[1]的专著. Shvydkoy[2]和Sun[3]等研究关于三维稳态齐次解与轴对称解的工作. 对Boussinesq方程组，Majda[4]收集了一些经典的显式解. 2014年，Chae-Constantin-Wu[5]在一个二维的锥上，在特殊条件下把Boussinesq方程组去耦为二维Euler方程和一条传输方程，从而得到一些温度梯度有快速增长的解. 文献[6]中利用二维Boussinesq方程和三维Euler方程的相似性找到一些三维Euler方程组的显式解. 文献[7]中推广了文献[5]中去耦的方法，在各种光滑区域上找到类似的解. 由于要满足边界条件，解的存在区域都是不规则的.

另外，显式解或可对解决领域中的开问题提供一些线索. 近年关于不可压理想流体的大问题是它们的全局正则性，即对三维Euler方程和二维，三维Boussinesq方程组，局部光滑解可否在有限时间失去正则性. 2019年，Elgindi[8]，Elgindi-Ghoul-Masmoudi[9]在这个问题上取得了很大的进展. 2014年Luo-Hou[10](也参看文献[11])提出了一种在柱体上的Euler方程局部光滑解在有限时间爆破的情景，给出一个初值，它引发出的局部光滑解可能在有限时间爆破，并提供数值计算结果支持. 另一个相关的问题是二维Euler方程的涡量梯度的增长. 众所周知，它的极大模相对于时间最多只可有双指数增长. 2015年Kiselev-Sverak[12]证明这增长率可以在流场的双曲点附近达到. Zlatos[13]证明了达到这极大增长率的范围比文献[12]中的范围大，虽然仍然很小. 这现象能否在区域中大范围发生是广受关注的问题. 本研究试着找这些方程的初值问题(或一些特殊情况)的解的公式，希望它们能够提供探索以上两个问题的提示，或退一或多步在一些对称区域上找一些显式解. 笔者是从分离变量出发找到一些显式稳态解.

1 Euler方程的稳态解

以下引理收集了本文中需要的贝塞尔函数的性质.

引理令N*为正整数集合，ν∈(0,∞)，k∈N*，x∈[0,∞).

a)ν-阶第一类贝塞尔函数(在正轴上的限制)是[14，p339]

(5)

整数阶第二类贝塞尔函数是[14，p357]

(6)

c) 令φ:[0,∞)→R是满足φ(0)≠0的一般光滑函数(在各式子中，甚至等号两边，φ可以不同). 则

(7)

(8)

(9)

e)由文献[14，p369]，当x→∞，

f)Jν(x),Yk(x)有可数个正零点，若排成上升列，它们趋向+∞.

g) 对x≥0，x/2-J1(x)≥0，且x>0时严格大于0.

引理的证明由(5)-(6)式得(c)-(d). 由e)得f). 下证g).

令h(x)=x/2-J1(x)，则h(0)=h′(0)=0.当x∈(0,5/2]，J″1(x)是交错级数，从而小于它的首项，所以J″1(x)<0，h″(x)>0，h′(x)>0，h(x)>0.又知J1的最大值点是在(0,5/2]中[15]，所以对x>0，h(x)>0，知(g)成立.

定理1令Ω为开圆盘B(0,L),L>0.对k,n∈N*，α∈R，

(10)

定理1的证明可把上述公式代入(2)式直接验证.本文中约定，(2)i是指(2)式中第i个方程，i=1，2，3.为了解释求得这些解的方法，我们做以下推理.

第一步，先在B(0,L)-{(0,0)}上解(2)式且要求ω，u有界. 从分离变量开始，观察(2)式的形式，试找以下形式的解:

ur(r,θ)=r-1F(r)kcos(kθ+α),k=1,2,3,…,α∈R，

其中F:[0,L]→R满足F(L)=0(使ur(L,θ)=0,从而在∂B(0,L)上u·n=0).则从(2)2得ψθ=-rur=-F(r)kcos(kθ+α)，取ψ=-F(r)sin(kθ+α)，从而uθ=ψr=-F′(r)sin(kθ+α).由(2)2得

ω(r,θ)=[-F″(r)-r-1F′(r)+r-2k2F(r)]sin(kθ+α)=Φk(r)sinΘk

(11)

其中Φk(r):=-F″(r)-r-1F′(r)+r-2k2F(r)，Θk:=kθ+α，则

ωr(r,θ)=Φ′k(r)sinΘk，ωθ(r,θ)=Φk(r)kcosΘk.

由(2)1得

r-1F(r)kcosΘkΦ′k(r)sinΘk-r-1F′(r)sinΘkΦk(r)kcosΘk=0，

即F(r)Φ′k(r)-F′(r)Φk(r)=0，所以∂r[Φk(r)/F(r)]=0，得Φk(r)=dF(r)，d∈R.

下面求F有界且使边界条件(2)3成立:

(12)

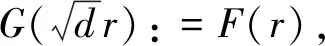
G″(s)+s-1G′(s)+(1-s-2k2)G(s)=0

(13)

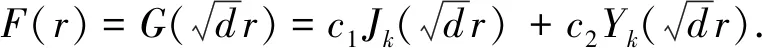
(14)

则Fk,n(r)满足(12)2.把Fk,n(r)代入(11)式得(10)式.

以下证明ω，ui可C1地、ψ可以C2地拓展到(0,0)，并在该点处满足(2)式.

第二步，我们断言对k,n∈N*，u可以连续地扩张到(0,0)为

(15)

因为该处没有极坐标，我们要用欧氏坐标讨论. 从

u(x1,x2)=u1(x1,x2)e1+u2(x1,x2)e2=ur(r,θ)er+uθ(r,θ)eθ

得

u1(r,θ)=r-1Fk,n(r)kcos(kθ+α)cosθ+F′k,n(r)sin(kθ+α)sinθ

(16)

u2(r,θ)=r-1Fk,n(r)kcos(kθ+α)sinθ-F′k,n(r)sin(kθ+α)cosθ

(17)

从(7)、(8)、(14)式得

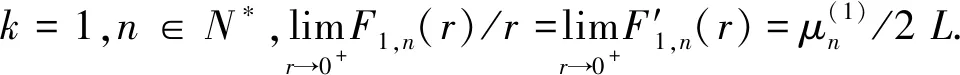
(18)

(19)

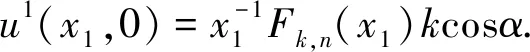
=Ik+IIk.

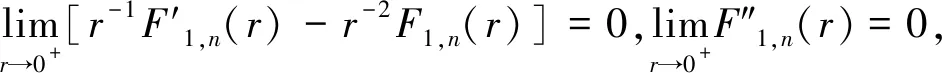
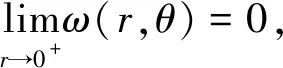
ω(0,0)=0

(20)

则ω在(0,0)处连续. 我们断言，

(21)

证明如下.

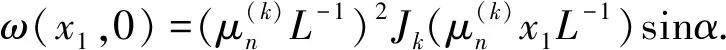
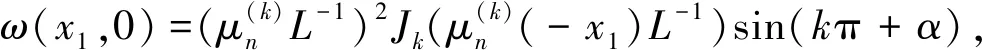
左右导数相等，则ωx1(0,0)存在. 同理可证(21)式成立.

最后证ωx1(0,0)，ωx2(0,0)在(0,0)连续. 当(x1,x2)≠(0,0)，

从(7)、(8)式得

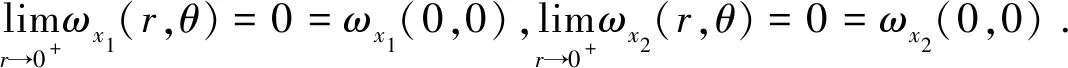
即ωx1(0,0)，ωx2(0,0)在(0,0)处连续.

第六步，证明ψ可以C2地拓展到(0,0).只要证明ψ可连续地拓展到(0,0)，ψx1(0,0)=u2(0,0)，-ψx2(0,0)=u1(0,0)，则可知在B(0,L)内，⊥ψ=u.再从已证的u∈C1(B(0,L))，则可得到ψ∈C2(B(0,L)).从(14)式与第一步第一段中的式子知由(7)式得若令ψ(0,0)=0，则ψ在该处也连续.再讨论ψ在(0,0)处的偏导.

由(7)式得，ψ在(0,0)处的右导数是

左导数是

类似地，可得-ψx2(0,0)=u1(0,0).定理得证.

积分得

从而

其中C是常数. 事实上，只从Jk，sin(kθ+α)在各区域的符号就可以描出图1中的轨迹.

图1 定理1中k=1，n=3，α=0时的情况. (a)和(b)分别显示ur，uθ的符号，(c)是质点轨迹，当中实线圆跟x1-轴的6个交点是流场的双曲点. 当k，n增大，双曲点在圆盘中可以任意稠密.

从图1可见在很多角对称区域，及它们的随意并，边界条件(2)3都被满足. 我们有以下定理.

(22)

对应的速度场是

注1) 圆环区域(r,θ)∈(a,b)×[0,2π]是a)中区域的特例情况，此时，θ0=2π，从而ν=N/2，N是正整数.当N是偶数，得如定理1中的整数阶贝塞尔函数. 当N是奇数时，JN/2有较简单的表达式(引理b)).

2) 锥(r,θ)∈(0,∞)×(γ,γ+θ0)(包括半平面)是b)在a=0时的特殊情况. 对任何d∈(0,∞)，令

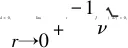
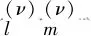
定理2的证明与定理1的证明相似，但对F要求F(a)=F(b)=0(使在r=a,b处ur≡0)，且ν=Nπ/θ0一般不是整数，所以涉及非整数ν的贝塞尔函数

2 Boussinesq方程的稳态解

本节考虑半平面和全平面上Boussinesq方程(4)的稳态解. 在有界角对称区域上(例如圆盘)，由引理g)，不可能在有限圆盘上找到满足边界条件ur=0的解，所以只讨论这两种情况.

定理3令H为上半平面，(r,θ)∈(0,∞)×(0,π)，(4)式在H上有解

i)

(23)

其中J1为贝塞尔函数，d>0,c∈R.对应的速度场和流函数是

ii)

其中a∈R.对应的速度场和流函数分别是

ur(r,θ)=ar2cosθ，uθ(r,θ)=-3ar2sinθ，ψ(r,θ)=-ar3sinθ.

定理3的证明可以把(23)式直接代入(4)式验证.本文中约定，(4)i表示(4)式中第i个方程，i=1，2，3. 为了解释得到该解的方法，我们做以下的推理. 从分离变量出发，通过观察(4)1的形式，我们找形如ur(r,θ)=r-1F(r)cosθ的解，F待定. 跟定理1 Euler方程的情况不一样，(4)1的右边有cosθ,sinθ出现，以致不能找到形如ur(r,θ)=r-1F(r)kcoskθ，k≥2，的解. 由(4)3得ψθ=-F(r)cosθ，取ψ=-F(r)sinθ，从而uθ=ψr=-F′(r)sinθ(这已保证uθ在∂H-{(0,0)}是0，(4)4在这里满足). 从(4)3ω=Φ(r)sinθ，其中Φ(r)=-F″(r)-r-1F′(r)+r-2F(r).因此ωr=Φ′(r)sinθ,ωθ=Φ(r)cosθ.(4)1的左方为[r-1F(r)cosθ]Φ′(r)sinθ-r-1[F′(r)sinθ]Φ(r)cosθ.

观察(4)1的形式，令ρ(r,θ)=g(r)sinθ，g待定. 则ρr=g′(r)sinθ，ρθ=g(r)cosθ.代入(4)2得Fg′-F′g=0，从而[g/F]′=0，g(r)=cF(r),c∈R.再代入(4)1得

[r-1F(r)cosθ]Φ′(r)sinθ+r-1[-F′(r)sinθ]Φ(r)cosθ=[g′(r)-r-1g(r)]sinθcosθ

(24)

即F(r)Φ′(r)-F′(r)Φ(r)=rg′(r)-g(r)=crF′(r)-cF(r).两边同乘以F-2得∂r[Φ(r)F-1(r)]=-c∂r[rF-1(r)]，积分得F″(r)+r-1F′(r)+(d-r-2)F(r)=cr，c,d∈R

(25)

G″(s)+s-1G′(s)+(1-s-2)G(s)=csd-3/2

(26)

若d=0，(25)式退化为F″(r)+r-1F′(r)-r-2F(r)=cr，其通解为F(r)=ar3,a=c/8，a∈R.(4)式有解ω(r,θ)=-8arsinθ，ρ(r,θ)=8a2r3sinθ.

定理得证.

定理4在全平面R2上(4)式的解为

(27)

定理4的证明因为R2没有边界，所以(4)4是虚的.

第一步，类似于定理3的证明，得在R2{(0,0)}上的解

(28)

只需证明它们可以C1地、ψ可以C2地延拓到(0,0)，在该处满足(4)式.

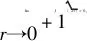
(29)

第三步，我们断言

(30)

可通过直接计算证明. 例如对ω，当x1>0，(x1,0)的极坐标是(r,θ)=(x1,0).由(28)式得ω在(0,0)处右导数是

而左导数是

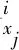
第五步，下证ψ可以C2地拓展到(0,0).类似于定理1第六步证法，令ψ(0,0)=0，则ψ在该点连续.又直接证明ψx1(0,0)=u2(0,0)，-ψx2(0,0)=u1(0,0)，则在R2上，⊥ψ=u.又由u∈C1，得ψ∈C2.

定理得证.