砂岩颗粒流平行黏结模型细观参数标定方法研究

黄宜胜 夏晓丹

(三峡大学 水利与环境学院，湖北 宜昌 443002)

1979年由Cundall等[1]提出的离散单元法PFC主要用于分析准静力或动力条件下的含节理岩体的力学问题，通过对刚性球体之间设置黏结材料，来实现颗粒之间力和力矩的传递.PFC数值模拟过程中的首要工作就是进行岩石细观参数标定，直接影响着最终结果的正确性和合理性，因此岩石细观参数标定是PFC数值模拟过程中一项极其重要的工作.

目前，基于颗粒流数值模拟的岩石细观参数标定已有较多研究成果.Benvenut等[2]提出了一种利用人工神经网络来标定离散元参数的方法.Yoon等[3]应用PB设计和响应曲面分析确定了适合岩石颗粒单轴压缩的微观参数.Hsieh等[4]结合颗粒模型揭示了砂岩宏观力学行为受微观性质影响的变化规律.陈鹏宇等[5,6]、刘相如等[7]对平直节理模型中的细观参数进行了参数标定研究.徐小敏等[8]对基于线性接触模型的颗粒材料宏细观参数进行了研究.夏明等[9]对簇平行黏结模型中宏细观参数间的影响进行了研究.丛宇等[10]、阿比尔的等[11]采用变量分析法研究了平行黏结模型宏细观力学参数相关性.赵国彦等[12]采用理论与数值模拟相结合的方法研究了平行黏结模型中部分细观参数对宏观特性的影响.牛双建等[13]研究了细观参数对砂岩材料宏观参数的影响规律.

本文在前人研究的基础上，基于砂岩的单轴压缩试验结果，采用正交设计方法对多个细观参数进行了敏感性分析，得出了各细观参数对试验数据影响的敏感度，合理标定出了砂岩的细观参数.平行黏结模型需要标定的参数较多，为了简化参数的标定工作，降低数值试验的次数，需要先对宏细观参数之间的关系进行分析.近年来，颗粒流数值模拟方法被广泛应用于岩土工程中[14,15]，如何正确有效地标定能够真实反映岩石宏观参数特性的细观参数就显得尤为重要.

1 平行黏结模型理论

在PFC模型中，允许颗粒间接触的黏结模型有点接触模型和平行模型.点接触黏结模型发生在近似于接触点很小的范围内，仅限于传递力；平行黏结模型发生在接触颗粒间具有一定形状和尺寸的黏结范围内，传递力的同时传递力矩.平行黏结模型能够形成裂纹，与实际岩石的微弱结构面类似，它能基本反映岩石结构面的破坏过程.

2 颗粒流数值模拟试验

2.1 颗粒流数值模型

数值试验在颗粒流离散元软件PFC2D上完成，选择平行黏结模型作为接触本构模型.单轴压缩试验数值模型尺寸为直径50 mm、高100 mm，采用wall命令模拟构建模型边界及其受力环境，用上、下墙来模拟轴向加卸载功能.上、下墙体相向缓慢移动加载试样，加载速率0.005 m/s，如图1(a)所示，得到的应力-应变曲线如图1(b)所示.

图1 基于PFC2D的单轴压缩实验

2.2 岩石数值实验

单轴压缩试验是由宏观参数得到细观参数的重要途径之一，测得的宏观参数有弹性模量E、泊松比ν、抗压强度σf.根据数值试验的应力-应变曲线可得平面应力状态下的弹性模量E和泊松比ν，见式(1)、式(2)[5]：

(1)

(2)

式中：σ50、ε50分别为峰值强度50%处对应的轴向应力和轴向应变；εx50、εy50分别为σ50所对应的横向应变和轴向应变.

2.3 正交试验设计

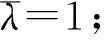
通过查阅相关资料[5，10，17，18]并结合具体实际，最终确定各项参数的4个因素水平数取值见表1.在表1基础上设计了PFC模型细观参数正交序列，进行单轴压缩数值模拟试验并得到宏观参数：弹性模量E，泊松比ν、抗压强度σf，见表2.从表2可以看出计算的宏观参数基本符合砂岩参数取值范围(抗压强度20～170 MPa，弹性模量3～80 GPa，泊松比0.20～0.30)[19].

表1 平行黏结模型细观参数正交试验设计表

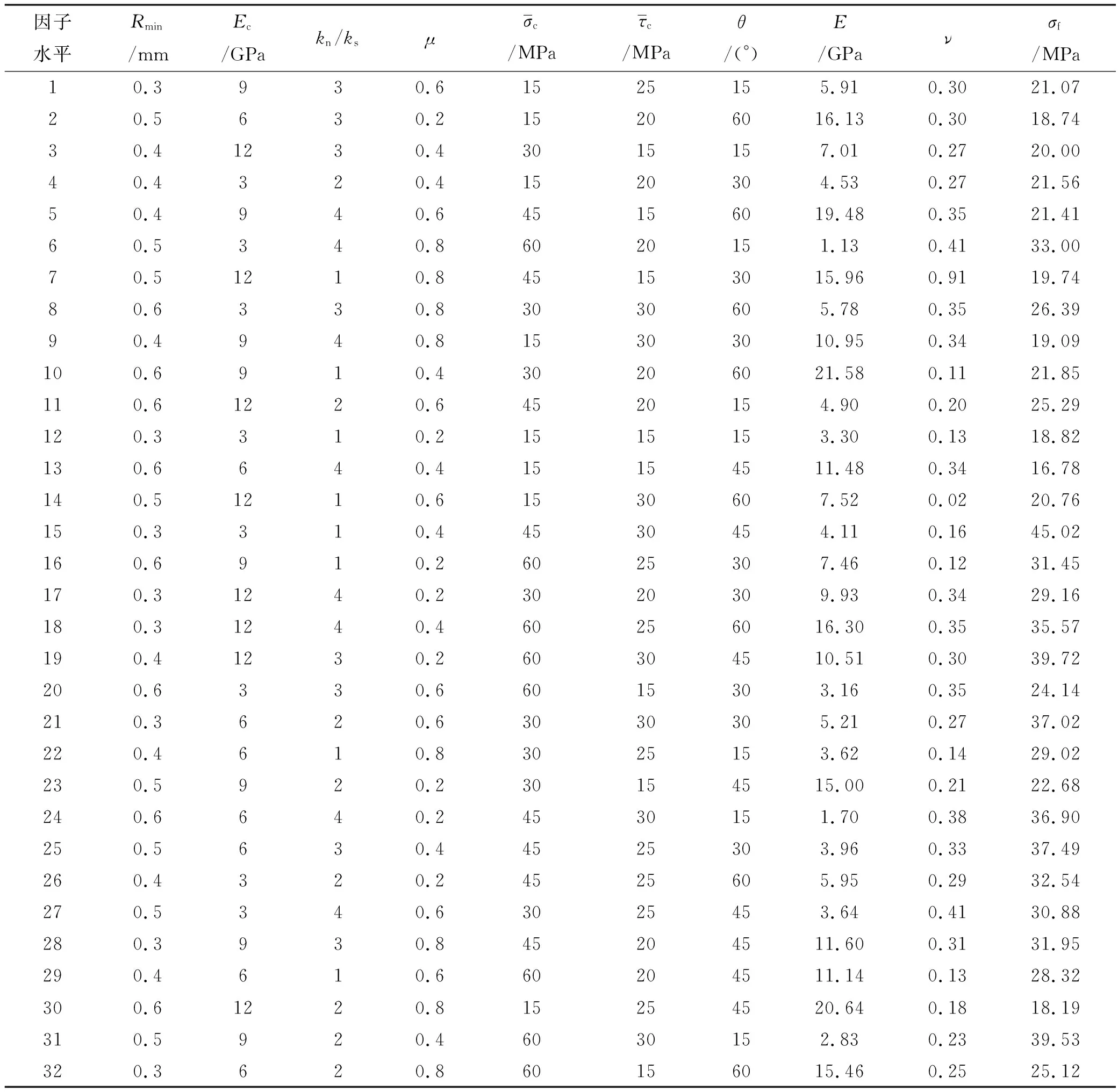
表2 正交设计矩阵序列及宏观参数结果表

3 宏细观参数的影响分析

3.1 多因素方差分析

常用F统计量分析多个因素对因变量的影响程度，用来检验多个因素不同取值水平的组合形式，以及多个因素对因变量是否产生显著性影响.多因素方差分析除了能够研究多个因素对因变量之间的独立影响，还能够分析多个因素之间的交互作用是否会对结果产生显著性影响.本文选用SPSS软件进行多因素方差分析，对各因素的主效应进行分析，得出F统计量和相伴概率sig.值，sig.值用于检验细观参数是否对宏观参数产生显著性影响.若sig.<0.01，则产生了非常显著的影响；若0.010.05，则影响不显著.分析结果如图2所示.

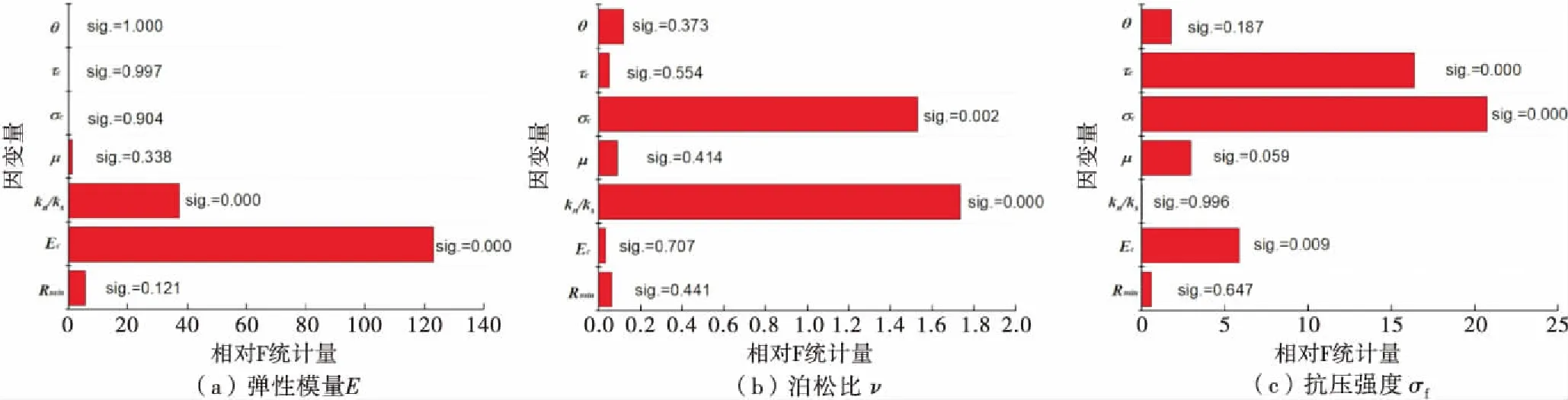
图2 多因素方差分析的F统计量图

根据图2中F统计量大小及相伴概率sig.值，可以判断各细观参数对岩石宏观力学参数影响的敏感性程度.具体描述如下：

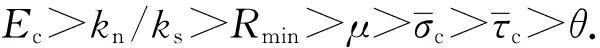
3.2 回归分析

基于以上正交设计的模拟结果进行回归分析，建立宏观参数与其主要影响因素之间的关系式.采用逐步回归法进行回归分析，仅选用sig.≤0.01所对应的影响非常显著的细观参数.设置变量进入的概率门槛值为0.05，删除概率门槛值为0.01.取显著性水平α=0.05作为回归系数检验的标准.

弹性模量E的显著性影响因素主要有颗粒黏结模量Ec和颗粒刚度比kn/ks，对这两个因素进行线性回归，得到公式(3)，拟合系数R2=0.996，拟合效果较好.

(3)

由式(3)可知，弹性模量E与平行黏结模量Ec呈正相关，与颗粒刚度比kn/ks呈负相关.

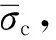
(4)

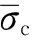
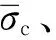
(5)

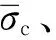
4 实例验证

4.1 岩石细观参数公式确定

因为宏细观参数之间具有相关性，也可建立细观参数为因变量、宏观参数为自变量的线性回归关系式.跟上述方法一致，采用逐步回归法，通过SPSS软件实现，拟合结果见表3.

表3 砂岩细观参数与宏观参数之间回归关系式及拟合系数表

表3中线性拟合系数在0.828～0.968之间，拟合效果较好.上述线性拟合公式可用于确定砂岩细观参数，根据砂岩细观参数进行PFC数值模拟试验，计算出宏观参数，进一步与室内试验数据对比.

4.2 试验结果对比

由上述方差分析结果可知，摩擦系数μ和平行黏结内摩擦角θ对弹性模量E、泊松比ν、抗压强度σf几乎没有影响，根据前人经验[7,15]，在进行细观参数标定时，可取tanθ=0.5作为初始值，则μ=0.519，将其近似地取为0.5.最小半径Rmin对任何宏观参数都没有造成非常显著性的影响，说明粒径的改变对岩石宏观特性的影响不大，为了合理设置计算精度和提高计算效率，选取Rmin=0.5 mm进行数值模拟[20].

为了验证细观参数标定公式的准确性，对3种砂岩室内试验结果[13,21,22]进行了颗粒流数值模拟研究.砂岩室内试验宏观力学参数见表4.由这3组数据依据表3中的公式进行计算得到各细观参数见表5，利用表5中的细观参数进行颗粒流数值模拟试验得到的砂岩应力-应变曲线如图3所示.

表4 砂岩室内试验宏观力学参数表

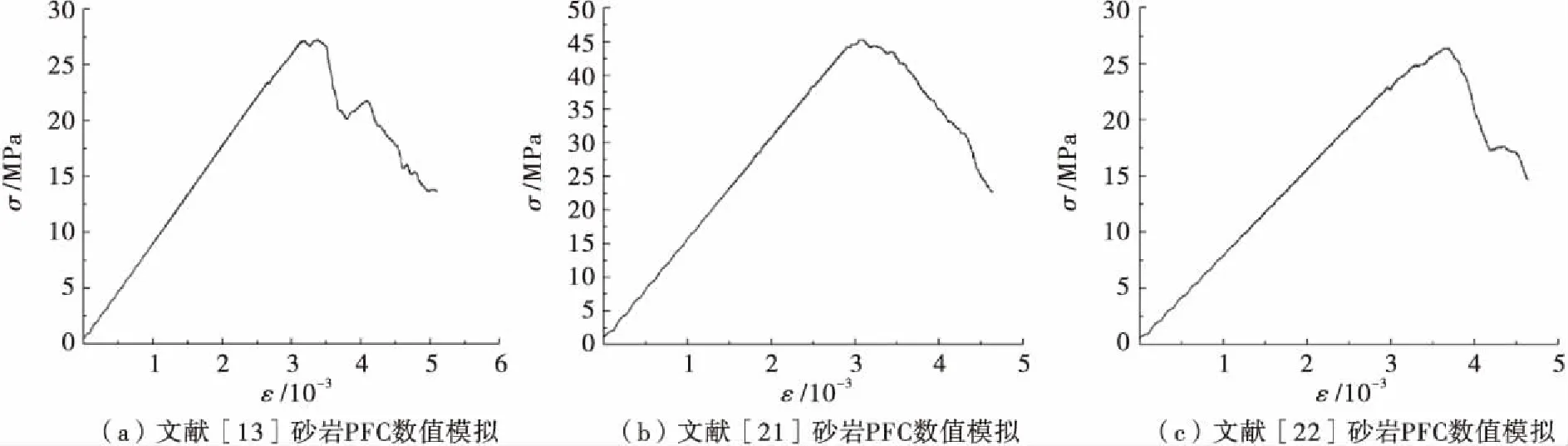
图3 砂岩单轴压缩PFC数值模拟应力-应变曲线图

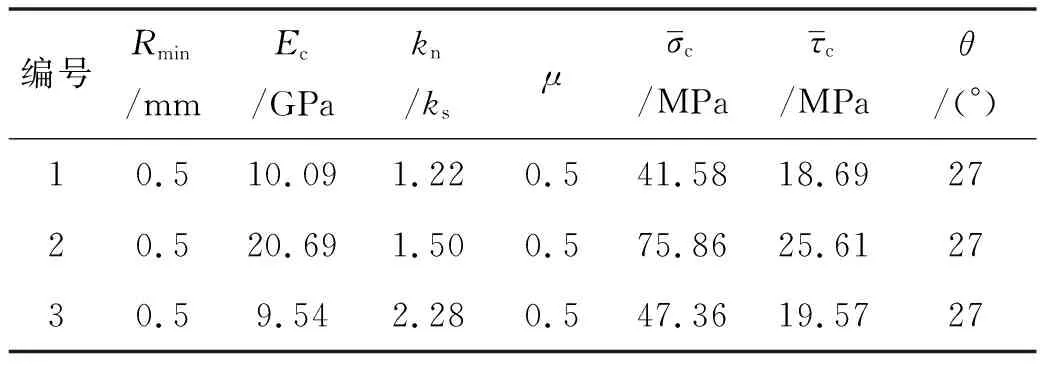
表5 平行黏结模型细观参数表

由表6可知，通过宏细观参数之间的关系式确定岩石细观力学参数，利用细观参数进行颗粒流数值模拟得到的结果与室内试验结果误差在10%以内，证明采用正交试验设计法标定的砂岩细观参数计算公式有效.

表6 砂岩的宏观力学参数对比表

5 结 论

1)基于正交设计试验，研究了7种细观参数对砂岩宏观特性的影响，基于平行黏结模型进行了单轴压缩试验PFC数值模拟，分析砂岩细观参数对抗压强度σf、弹性模量E、泊松比ν等宏观特性的影响，并根据影响大小对其进行排序，建立了砂岩宏观参数与细观参数之间的相关关系.

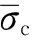
3)在进行PFC数值模拟试验前，根据以细观参数为因变量、宏观参数为自变量的关系式，初步标定数值模型的细观参数，进行砂岩的单轴压缩数值模拟试验.通过对比，发现PFC数值试验宏观参数与室内试验宏观参数较吻合，证明通过正交试验设计法标定的砂岩细观参数计算公式是可靠的.