初探极限思想在小学数学教学中的渗透策略
易常朝
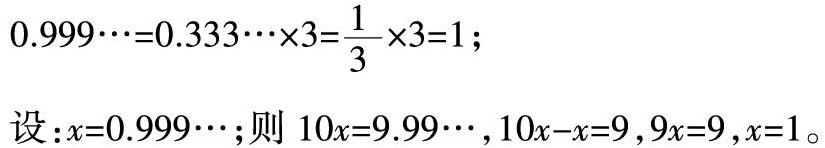

摘 要:极限思想属于推理思想中较低层次的一种数学思想。教师在教学中渗透极限思想可以加深学生对数学概念、定律、法则等的理解。据此,探讨在小学数学教学中渗透极限思想的策略。
关键词:小学数学;极限思想;渗透策略
数学思想蕴含在数学知识形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象与概括,如抽象、分类、归纳、演绎、模型等。多数专家认为数学思想是对数学知识的本质认识、理性认识。参与《义务教育数学课程标准(2011年版)》撰写及《义务教育数学课程标准(2011年版)》解读的专家学者认为,数学思想是有层次的,较高层次的基本思想有三个:抽象思想、推理思想、模型思想。极限思想是属于推理思想中较低层次的一种数学思想。在小学阶段所能渗透的数学思想方法中,极限思想是最为抽象、最难被理解与接受的一种数学思想,也容易被老师忽略。本文以“数与形”(例2)的教学为例,谈谈在小学阶段渗透极限思想的一些愚见。
一、极限思想的概念及其重要性
极限是用以描述变量在一定的变化过程中的终极的概念。极限的思想方法为建立微积分学提供了严格的理论基础,为数学的发展提供了有力的思想武器。极限可分为数列极限和函数极限。极限概念是非常抽象的,在小学数学教学中不曾涉及。作为专业的数学教师,要对其概念把控于心,细心琢磨,把这些抽象的概念转化成数学思想,循序渐进地渗透给小学生,绝不可以忽视它。
“数学广角”是人教版教材独有的内容。人教版教材安排“数学广角”的主要目的是向学生渗透数学思想及方法。教材根据学生的年龄特点从二年级开始每一册都安排了“数学广角”的内容。由王永春(2014)的研究可以看出,极限思想在“数学广角”中编排的例题只有一个,但不代表渗透极限思想的机会只有一次。极限思想在小学阶段渗透的机会不多,笔者梳理了人教版小学数学12册教材,发现可以渗透极限思想的内容如下表所列。
从上表可以看出,人教版教材针对数学思想方法专门编排了教学内容,但数学思想方法的渗透又不局限于“数学广角”这一类教学内容,需要教师在平时的教学中发掘與提炼。《义务教育数学课程标准(2011年版)》把数学思想方法作为数学“四基”中的“第三基”,并对数学思想方法的渗透做了明确的要求,也表明了它的重要性。
二、极限思想的渗透途径
小学生的年龄特点决定了他们对数量有限的具体事物容易理解,对数量无限的抽象事物较难把握。学生的生活经验、数学知识还比较贫乏,因此理解“无限逼近”一个数时用“等于”来表示是认知难点。笔者认为,渗透极限思想可以通过以下三个途径达成。
1.通过“有限”想象“无限”
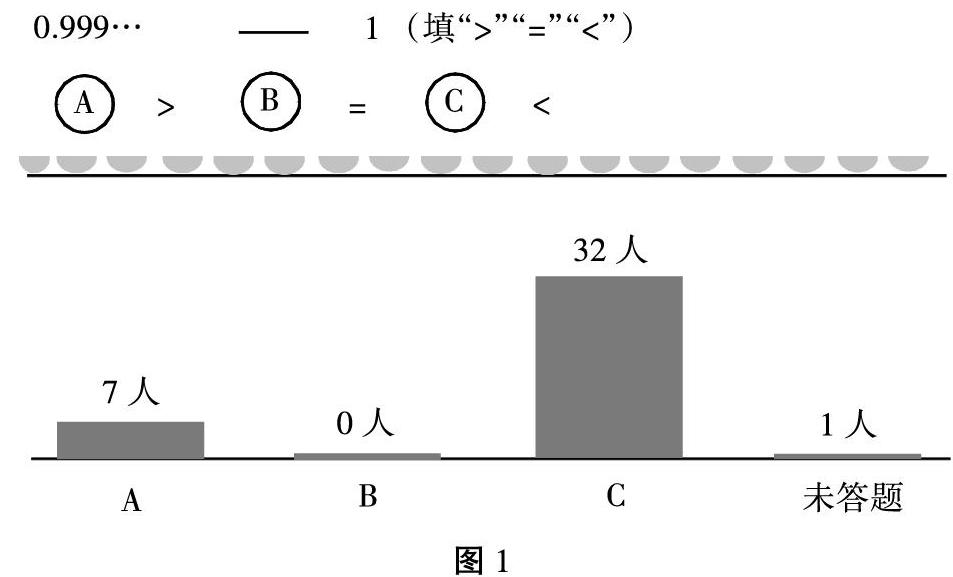
有限是具体的,可观察的,可计量的,也是小学生接触最多的数量形式。对于无限,小学生也不陌生,例如一年级认识自然数时就知道一直往下数是可以不停止的,到了大数的认识时,进一步知道0是最小的自然数;五年级接触到循环小数,又知道一个数也可以是写不完的,它的位数是无限的;在认识图形时知道直线和射线是可以无限延伸的。有限与无限在本质上区别很清楚,但我们都习惯用“有限的”眼光去看“无限的”的问题,课前的一个小测试就证明了这一观点。出示比大小的题目:0.999…○1,学生的作答结果如图1,几乎所有学生都选择了小于号,这也说明学生对“极限思想”的敏感度为0。0.999…这个循环小数是一个写不完的小数,他们认为:这个数不管后面有多少个9,总是要比1小一点点,是不可能等于1的。既然学生有此习惯,那就依学生的习惯设计活动,引导学生从“有限”走向“无限”。
【片段】以人教版义务教育教科书数学六年级上册15页的“你知道吗?”为题干,学生可以快速地解决此“有限”问题,用连加的方法列式并计算出来,并说明理由。
为了下一步的学习,教师有必要引导学生发现算式中相邻加数以及得数与最后一个加数的关系,再抛出三个问题引导学生想象“无限”。
(1)如果继续往下加,下一个加数应该是多少?
(2)如果一直这样无限地加下去,算式该如何写?
(3)你算得完吗?你能根据前面的规律想象出这个算式的得数吗?
少数学生可以大胆地猜测是一个接近1的数,他们的理由是:得数总等于1减去最后一个加数,而分母越来越大,那就和1就越来越接近。
学生用了“最后一个加数”这一词组,说明学生是把算式当作有限的加法进行思考的,但学生也知道找不到最后一个加数,就只能利用规律发现得数接近1。在这里,学生知道通过“有限”来想象“无限”了。
2.感受无限收敛
极限思想是用无限逼近的方式来研究数量的变化趋势的思想,这里要抓住两个关键语句:一是变化的量是无穷多个的,另一个是无限变化的量趋向于一个确定的常数。两者缺一不可。例如,自然数、奇数、偶数等是无限的,但它是趋向于无穷大,不趋向于一个确定的常数,因而它们没有极限;再如一个循环小数,它的小数部分的数字是写不完的,是“无限的”,但它也是没有极限的。反之,离开“无限”谈“极限”是毫无意义的。
“无限≠极限”的原因在于无限变化的量有两种形态:发散的与收敛的。前述两个例子虽然是无限的,但它们是发散的,因此它们没有极限,只有当变化的量是无限收敛时才存在极限。在计算圆的面积时,先把圆平均分成若干等份,再拼成一个近似的长方形。注意,这里是说一个“近似的”长方形,它不是一个真正的长方形,所以,不能按照长方形的面积计算方法来求圆的面积,把这个圆继续有限地平分下去,哪怕最小的扇形看起来只有一条线一样那么小,都无法拼成一个真正的长方形,只能让学生感受到这个圆被这样无限平分后拼成的图形无限地接近长方形,就把圆的面积当作长方形的面积进行计算而得出圆的面积的计算公式。学生可能无暇顾及把近似的长方形当作是长方形进行计算是否合理,但可以让学生积累一些感性认识,埋下“极限”的种子。
3.理性认识极限
学生对片段中的算式,发现它的得数接近1是不难的,如果告诉他们是等于1,大多数人是无法接受的。他们认为,不管分到什么程度,总是会有剩下的,不可能全部被分完。又如前面所述例子中的0.999…这个无限循环小数,有的人认为它的位数是无限的,总比1相差一点点,不可能等于1。其实,这是一种错误的观点,是因为用“有限”的眼光看待“无限”所造成的。这时,就需要借助极限思想,这也是极限思想的关键所在。
在推导圓的面积计算公式过程中,把这个圆无限地平分下去,拼成的图形就无限地接近一个长方形,因此,长方形的面积是圆的面积的极限。对于0.999…这个无限循环小数,大家都已经认为它是接近1,要进一步地证明它等于1也不难。例如,一般来说,无限循环小数都可以化成一个最简分数,但0.999…这个无限循环小数无法化为一个最简分数,因为它等于1。一般有以下两种方法证明。
0.999…=0.333…×3=1/3×3=1;
设:x=0.999…;则10x=9.99…,10x-x=9,9x=9,x=1。
学生显然无法全部接受或理解“无限逼近”就是“等于”,从“无限逼近”到“等于”是很多人跳不过去的一道坎,因而证明“等于”显得很有必要。
三、小结与展望
学生数学思想的形成是靠不断的积累、不断的运用来形成的,能够主动运用数学思想解决问题是学生数学素养的具体表现,它应该贯穿数学学习的始终。用一节课就把极限思想渗透到学生脑海深处,那是不可能的,但至少要引起学生的注意,使之在以后的学习中遇到“无限”问题时不至于停留在“有限”的层面。
极限思想在小学阶段有一定的应用,不要求学生掌握极限思想,只要渗透即可。渗透该思想的机会要靠教师自己去把握,而且要准确把握渗透的度,以免增加学生的学习负担。在小学阶段有意识地渗透基本数学思想是课标要求,也可以加深学生对概念、公式、法则、定律的理解,拓宽学生的解题思路,提高学生的数学素养,也是素质教育的内涵所在,能为小学生数学思想方法的学习打下较好的基础。本文所论述的内容,希望能为广大同行抛砖引玉。
参考文献:
[1]王永春.小学数学与数学思想方法[M].上海:华东师范大学出版社,2014.
[2]华东师范大学数学系.数学分析[M].3版.北京:高等教育出版社,2001.
[3]高丽娟.浅谈小学数学极限思想方法及其教学[J].软件(电子版),2014(12):290.
[4]孙国元.对小学数学中极限思想的探讨[J].教育实践与研究,2013(22):78.

