浅谈化归与转化思想在高中数学教学中的应用

黄庆彬

新课程标准明确提出了高中生通过数学课程的学习要达到获“四基”、提“四能”的目标。获“四基”，即学生获得数学基础知识、基本的技能、思想和活动经验;提“四能”，即提高学生从数学角度发现并提出问题、分析和解决问題的四种能力。纵观近年来高考数学试题的编制及考查的内容，都很好地反映了课程改革理念，加大了数学思维能力的考查，注重学科思想方法的运用，这就要求教师在数学教学中要“两手抓”，既要加强基础知识与基本技能的教学，又要注意以素养为导向，以能力为重，加大各种思想方法的渗透。

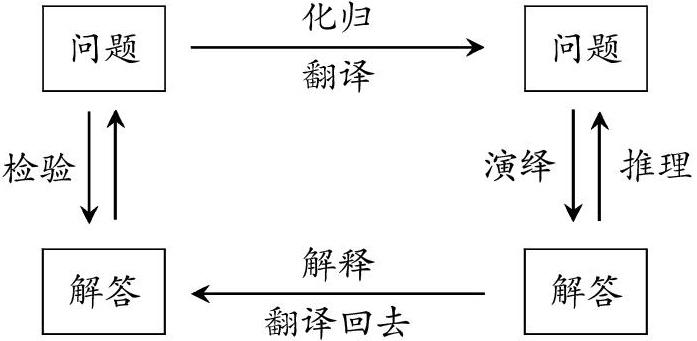
在中学数学思想方法中，最基本、最核心的就是化归与转化思想，它是解决数学问题思想方法的精髓。化归与转化，即运用转化、归结的数学手段，通过一定的数学过程，把一个复杂、陌生或者未解决的问题转化到已解决或较易解决的问题上来，从而破解原问题的一种方法。数学家笛卡尔对此方法给予了高度评价，称之为解决数学问题的万能方法。它对培养学生的解题能力和数学素质起至关重要的作用，故教师在平时教学中应注意引导学生抓基础与注重转化能力的培养两者并重，这是学好数学的金钥匙。以下便是其模式。

一、高中数学中应用转化与化归思想遵循的原则

应遵循4个原则：（1）熟悉化原则，即“化生为熟”，把陌生问题转化成熟悉问题。（2）简单化原则，即“化繁为简”，把复杂问题转化成简单问题。（3）直观化原则，即“化抽象为直观”，把较抽象的问题转化为较直观的问题（如数形结合思想，立体几何问题转化成平面几何问题）。（4）正难则反原则。若问题直接求解困难时，可考虑运用反证法或补集法，或用逆否命题间接地解决问题。

二、高中数学中常见的转化与化归方法

共有10种：在解决数学问题时，有的可用直接转换法、换元法、数形结合法，有的可用参数法、构造法、坐标法，还有的可用类比法、特殊法、一般化、等价转换法来解。这些方法在一些题目中可能单独使用，也可能相互交叉使用，是不能完全分割开的。

三、高中数学中转化与化归思想主要的应用情形

主要有6种：（1）在三角函数和解三角形问题中，公式的“三用（顺用、逆用、变形用）”、角度的转化、函数的转化、通过正弦定理和余弦定理实现边角关系的相互转化等。（2）函数问题中，把一个较难或较复杂的函数、方程、不等式转化为较简单、较容易的函数、方程、不等式。（3）在有平面向量与三角函数，又有平面几何、解析几何的交叉综合题目中，进行语言相互转化。（4）将一般的陌生的数列转化为常见的等差数列或等比数列求解。（5）将函数的单调性、极值（最值）、切线问题转化为其导函数f'（x）构成的方程、不等式问题来求解。（6）有关解析几何、立体几何的问题，常常用数形结合思想，通过数形转化来解决。

四、结合例题浅析高中数学中转化与化归思想的基本类型

1.特殊与一般的转化

当一个问题难以解决时，首先应观察这个问题的特殊与简单情况并分析，发现其中特殊的数量或关系结构或部分元素，然后推广至一般情形，从而完成从特殊问题到一般问题的解答，即所谓的特殊化的化归策略。有的数学题目具有一般性，有的则具有特殊性，解题时根据需要，要么化一般问题为特殊问题，要么化特殊问题为一般问题来解决。如何解这类题？关键点是：先确立转化对象，一般情况下把要解决的问题看成转化对象，接着寻找转化元素，也就是特殊元素和一般元素，然后再根据转化对象与特殊元素或一般元素的关系，把它转化为新的需要解决的问题，最后得出结论。这一类问题多以选择填空题的形式出现，难度适中，属中档题型。

题后反思：一般化与特殊化是解题过程中对一些一般性问题作特殊化处理，或把一些特殊问题作一般性处理。本题抓住了直线AB垂直于OP这个特殊情况，求出AB，MN的最小值和最大值，很好地解决了问题。

2.命题的等价转化

当遇到陌生或繁难的问题时，我们可运用等价转化的思想方法，把命题转化成我们熟知的基本问题，从而化繁为简、化生为熟。此类问题主要涉及函数、解析几何中有关存在性问题和排列组合中含有“至多”“至少”词语的题目。这一类问题多以选择填空题的形式出现，难度适中，属中档题型。

题后反思：遇到类似从正面难以解答，或运算较繁的问题，可先“反面进攻”，运用补集思想使正面得到解决。“正难则反”有时能带来“柳暗花明又一村”的解题妙处。

3.常量与变量的转化

在解决多变量的数学问题时，当题中的常量（或参数）在特定范围内取值，要求算出变量x的范围时，往往进行常量与变量之间角色的转化，即可选取其中的常数（或参数），把它看成变量，把变量当作常量，从而达到简化运算的目的。此类问题既有填空题也有解答题，难度适中，属中档题，主要涉及参数的取值范围问题。

4.函数、方程与不等式之间的转化

函数、方程与不等式三者之间联系密切，在解决方程、不等式的问题时常常需要用到函数这一解题工具，而解决函数的问题也往往离不开方程、不等式的数学工具，故借助函数、方程、不等式进行转化与化归，可将问题化繁为简，往往把不等式的恒成立问题转化为函数的最值问题，把证明不等式问题转化成函数的单调性与最值问题，把方程的求解问题转化成函数的零点问题、两个函数图象的交点问题等。

5.形体位置关系的转化

在立体几何中，遇到计算空间角和距离的题目时，往往要把它转化到平面内来求解。而形体位置关系的相互转化一般要先分析形体特征，根据形体特征确立需要转化的对象，然后进行位置转化，把不规则几何体通过切割、挖补、延展等方式转化为便于观察、计算的常见几何体。由于新的几何体是转化而来，一般需要对新的几何体的位置关系、数据情况进行分析，准确理解新的几何体的特征，最后在新的几何结构中解决目标问题。

题后反思：本题把立体几何问题转化为平面几何问题，把沿表面两点的距离问题转化为平面上两点间的距离问题。

在高中数学中，转化与化归思想是需要学生熟练掌握的重要且常用的思想方法，在一切数学思想方法中居于核心地位。教师在教学中应注重学生熟练运用转化与化归思想的训练，培养学生有意识地对问题进行灵活变换的学科思维，以利于提高学生解决数学问题的应变能力、分析解决问题能力，最终提高学科素养和数学能力。