“理法相融”中的分数概念深度学习

林志辉 陈柯柯

【摘 要】学生对分数的“部分与整体”意义理解不是一蹴而就的，分数的简单计算虽是一节同分母计算课，却承担着丰富分数概念的教学价值。本节课在“分吃一块巧克力”的大情境中，在大活动的推进里，在大问题的引领下，围绕算法的探究、迁移和融通，从算理的明晰走向算理的深化和内化，进一步丰富了学生对分数“部分与整体关系”的意义理解，实现从程序性的知识学习走向理解性的深度学习。

【关键词】分数  同分母  简单计算

教学内容：人教版数学三年级上册P96、P97。

分數的意义理解及运算是小学课程的重要内容，第一学段对分数意义的理解主要集中在“部分与整体关系”的意义理解。本课作为“分数的初步认识”的后续课例，同样也承载着促进学生对分数的“部分与整体”意义理解的要求。那么，如何在一堂计算课中丰富分数概念呢？

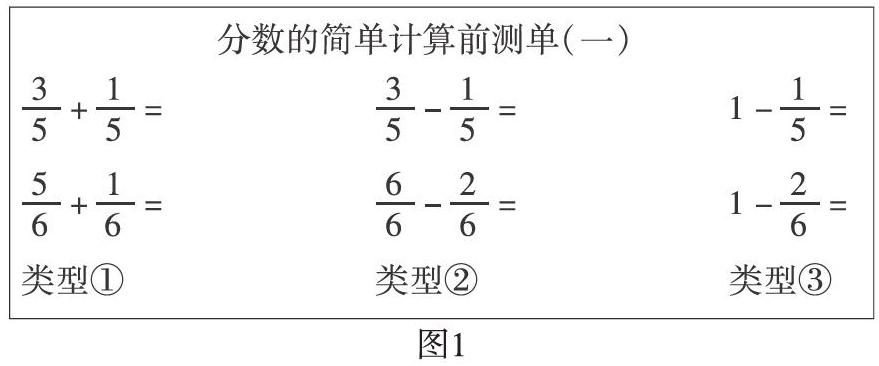
学生对于分数的加减都有了怎样的认知起点呢？为此，笔者抽样属地农村及城市三年级165名学生进行分母为10以内的同分母分数相加减的前测（如图1）。

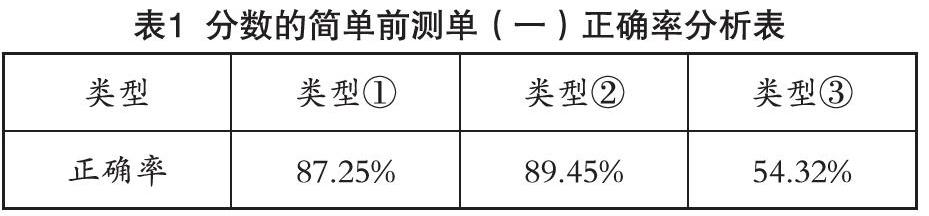
从前测反馈中（如表1）可以很明显地看到学生基本都已掌握同分母分数加减法的算法，这样的课堂里我们教什么？课堂的增量在哪里？深度学习是理解性的学习，如何带领学生从已知的程序性知识走向理解性学习是笔者在思考的。

数学课程标准中要求“能结合具体情境初步认识分数，会分母小于10的同分母分数加减运算”，这里的“结合具体情境”明确了应在结合情境表征的情况下学习分数。对比多个版本教材，都编排了大量的图形、情境、文字与符号等不同表征及多种表征相互转换的内容。学生会算，就表示他们真的明白为什么这样算吗？它们的表征情况又如何呢？于是，笔者展开了进一步的前测（如图2）。

笔者通过提供具体情境，让学生尝试通过画一画直观表征算理，写一写符号表征算式（如图2），发现学生算理表征的正确率并不高，即学生知其然却不知其所以然。由此，我们确定了以多元表征为载体，以理法相融为路径，丰富分数的概念意义的教学方式。

一、情境导入，激活概念

师：假如这是一块巧克力，把它平均分成2份，再把剩下的部分又平均分成2份。你能看到哪个分数？你是怎么想的？（如图3）有几个这样的分数？

学生提出看到2个 ，4个。

设计意图：通过巧克力的均分，促进学生对分数“部分与整体”意义的理解，为进一步学习分数加减的算理埋下伏笔。

二、理法勾连，丰富概念

1.算法探究，明晰算理

师（出示图4）：你更赞成哪种？

生1：我支持右边的，8+8=16，2+1=3，所以就是。

生2：我支持左边的，妈妈说过只用加分子，分母是不变的。

师（出示图5）：现在你又怎么想？同桌互相交流。

生1：我支持左边的，吃的一直是同一块巧克力，这块巧克力只被分成8份，而不是16份。

生2：对，这块巧克力被平均分成8份，先吃了2份，再吃了1份，吃了这8份里的3份，所以是。

生3：2个加1个等于3个，就是。

师：你们是这个意思吗？（播放学生直观表征视频）

师：为什么+ 不等于呢？

生：比还要小，越加越小了。

（教师课件呈现色块比较大小，如图6）

设计意图：图形的表征是学生真实的分数加减前概念，当学生在辨析中进行表征互通，将抽象的数运算具象地表达出来。通过结果的大小比较，让学生从不同的维度意识到分母相加是错误的，这样不仅开拓了学生的思维路径，更对数感有了一定的培养，增强了思维的双向性。

2.算法运用，内化算理

师：和你的小伙伴一起“吃”一块巧克力，你们会怎么“吃”呢？

（学生完成“课内活动单（一），同桌分吃巧克力”）

（教师反馈学生作品）

师（如图7）：想象一下图怎么画。

生：我想他可能是一个人吃了里面的4份，另一个人吃了1份。

师（如图8）：真会推测，那同学A比同学B多吃了几分之几呢？

生1：多吃了，同学A吃了6份里的4份，同学B吃了其中的1份。

生2：同学A吃了4个，同学B吃了其中的1个，列式就是                      。

师：你觉得他们是怎么吃的呢？

生1：我觉得可能是一个人吃了其中的3份，另一个人吃了其中的2份。

生2：我猜可能是一个人吃了，另一个人没有吃。

生3：可能和前面一幅作品吃得一样多。

师：他们俩谁吃得多，多吃了几分之几呢？

生1：同学A比同学B多吃了1份，也就是。

生2：3个比2个多1个，列式就是。

师（如图11）：现在一共吃了几分之几？

生1：一个人可能吃了，另一个人吃了，算式可以写成。

生2：我觉得整块巧克力都吃完了，还可以写作1，所以算式还可以写成。

设计意图：通过看算式猜图，看图猜算式，这样双向的作品反馈，互译直观的图形表征和抽象的符号表征，学生的表达从模糊走向精准，不断丰富对分数概念的认识。

（三）聚焦疑难，深化算理

师：我也想和你们一起分着吃，你们打算吃多少，留给我多少呢？

学生完成“课内活动单（二），和老师分吃巧克力”。

师（如图12）：你觉得他是怎么分这块巧克力的？你能想象他画的图吗？

生：平均分成了4份，他吃了，给老师留了。（如图13）

师（如图14）：你觉得他会怎么列算式？

生1：我猜他会列成。

生2：我觉得他会列成，因为1=，所以可以直接写成1减啊！

（师拓展“1-（）”，并用几何画板动态展示）（如图15）

图15 课件演示“1-（）”

设计意图：等值分数是学生在求解“                     ”的主要难点，本环节通过3层表征互通，逐一破解。第一次展示学生的作品，通过看算式猜图、看圖猜算式，不断让学生感悟到分数部分与整体及测量的概念。接着展示第二层次的作品，让学生意识到还能写成的格式，将上一个环节中的等值分数进行迁移。最后通过几何画板的动态增加功能，将一块巧克力不断细分，通过极限的思维将等值分数进行破解。

三、拓展提升，延展概念

师（如图16）：我这里有一块巧克力，你知道我吃了多少巧克力吗？

生1：，因为平均分成4份，巧克力占了3份。

生2：，因为。

师（如图17）：继续分，现在呢？

生1：平均分成8份，吃了7份，所以是。

生2：。

师：继续不断分下去，现在呢？（如图18）你们怎么这么快就知道了？

生：原来我是切割的，但是现在切小了之后越来越难数了，还是前面同学们的1减去空白部分算得快，所以我直接用，把1想成，这样就快了。

师：继续想象，不断细分下去，你还能知道我吃了几份吗？

生：只要把1想成几分之几，然后减去空白就可以了！

设计意图：学生的两种思路（累加色块和单位1减空白）各有千秋，在语言表征、图形表征和符号表征的勾连中理解了分数加减的算理，丰富了分数的概念。

【反思】

大情境——素材结构化

从前测、新授到练习，一直沿用分巧克力这一情境，充分发掘资源素材。从练习环节的同桌同吃长方形巧克力，到和老师分吃圆形巧克力，再到拓展题中的正方形巧克力，学生在结构化的素材中不断丰富了对分数概念的理解。

学生通过情境表征、图形表征、语言表征和符号表征间的互通、互译、互联，唤醒原本深藏不露的知识前概念和方法元认知，在表征的勾连中，对算法与算理的理解更清晰、更深刻！