以问题引导自主探究促进深度学习

杨梅芳

摘要：本文以《一次函数的图像（1）》教学设计为例，阐述问题在诱发学生思维、促进学生深度学习中的积极性作用，并提出创设问题时，要注意规划复习问题，精准切入，揭示新知生长点;创设情境问题，步步追问，引导自主探究;布局展延问题，层层递进，实现深度思维;设好小结问题，提炼整理，诱发继续探索的相关问题，供有关教师参考。

关键词：问题;生长点;自主探究;深度思维

中图分类号：G633.6 文献标识码：A文章编号：1992-7711（2021）07-091

数学教学是培养学生思维的教学，而培养学生的思维要依靠课堂上由问题产生的问题的引导，一个个悬念吸引着学生，思维的火花能时时迸发，课堂效率也就能大大提高。因此，要让课堂充满思维、充满智慧、充满探求，必须设置一系列能激起思维、引发探求欲的精彩问题，以此促进学生的真学习、深度学习。

一、教学案例

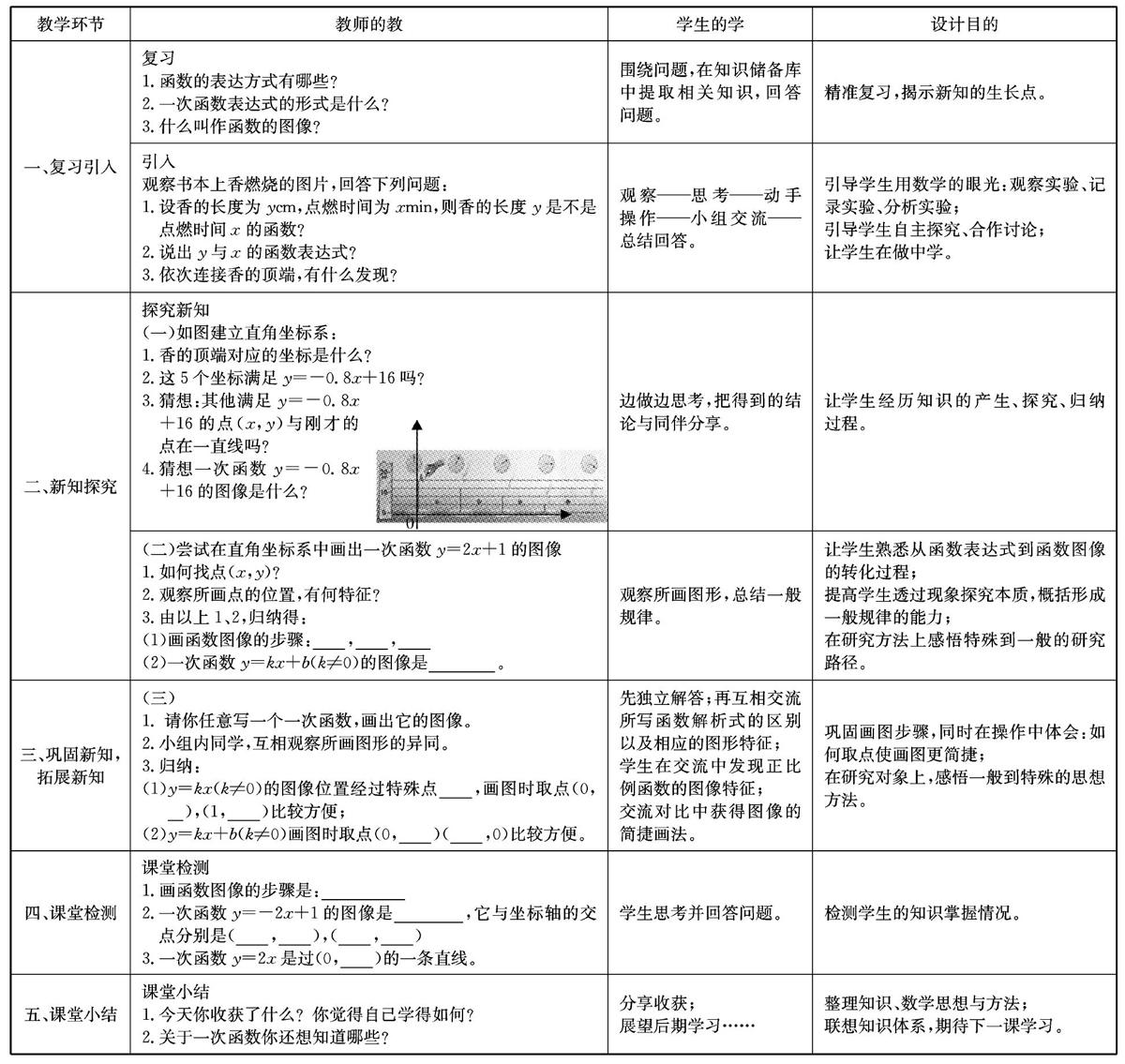
以《一次函数的图像（1）》教学设计为例，阐述问题在诱发学生思维、促进学生深度学习中的积极性作用。

教学环节教师的教学生的学设计目的

一、复习引入

复习

1.函数的表达方式有哪些？

2.一次函数表达式的形式是什么？

3.什么叫作函数的图像？围绕问题，在知识储备库中提取相关知识，回答问题。精准复习，揭示新知的生长点。

引入

观察书本上香燃烧的图片，回答下列问题：

1.设香的长度为ycm，点燃时间为xmin，则香的长度y是不是点燃时间x的函数？

2.说出y与x的函数表达式？

3.依次连接香的顶端，有什么发现？观察——思考——动手操作——小组交流——总结回答。引导学生用数学的眼光：观察实验、记录实验、分析实验;

引导学生自主探究、合作讨论;

让学生在做中学。

二、新知探究

探究新知

（一）如图建立直角坐标系：

1.香的顶端对应的坐标是什么？

2.这5个坐标满足y=-0.8x+16吗？

3.猜想：其他满足y=-0.8x+16的点（x，y）与刚才的点在一直线吗？

4.猜想一次函数y=-0.8x+16的图像是什么？

边做边思考，把得到的结论与同伴分享。让学生经历知识的产生、探究、归纳过程。

（二）尝试在直角坐标系中画出一次函数y=2x+1的图像

1.如何找点（x，y）？

2.观察所画点的位置，有何特征？

3.由以上1、2，归纳得：

（1）畫函数图像的步骤：

，  ，

（2）一次函数y=kx+b（k≠0）的图像是_____________。 观察所画图形，总结一般规律。让学生熟悉从函数表达式到函数图像的转化过程;

提高学生透过现象探究本质，概括形成一般规律的能力;

在研究方法上感悟特殊到一般的研究路径。

三、巩固新知，

拓展新知（三）

1. 请你任意写一个一次函数，画出它的图像。

2.小组内同学，互相观察所画图形的异同。

3.归纳：

（1）y=kx（k≠0）的图像位置经过特殊点  ，画图时取点（0， ），（1，  ）比较方便;

（2）y=kx+b（k≠0）画图时取点（0，  ）（  ，0）比较方便。先独立解答;再互相交流所写函数解析式的区别以及相应的图形特征;

学生在交流中发现正比例函数的图像特征;

交流对比中获得图像的简捷画法。巩固画图步骤，同时在操作中体会：如何取点使画图更简捷;

在研究对象上，感悟一般到特殊的思想方法。

四、课堂检测课堂检测

1.画函数图像的步骤是：

2.一次函数y=-2x+1的图像是_____________，它与坐标轴的交点分别是（  ，  ），（  ，  ）

3.一次函数y=2x是过（0，  ）的一条直线。学生思考并回答问题。检测学生的知识掌握情况。

五、课堂小结课堂小结

1.今天你收获了什么？你觉得自己学得如何？

2.关于一次函数你还想知道哪些？分享收获;

展望后期学习……整理知识、数学思想与方法;

联想知识体系，期待下一课学习。

二、教学反思

创设问题，就是把知识的产生、发展、应用过程以问题的形式提出来，让学生去思考。目的鲜明地设问，可以使启发性更强，探究过程更高效。

1.规划复习问题，精准切入，揭示新知生长点。

复习问题要精准规划，不是简单的以上节课所学作为本节课复习的内容，而是要找准学习生长点，由旧知伸向新知。如此，可以使学生复习的指向更明确，为新课做好充分的知识准备，同时抓住数学知识的前后联系，精准切入，体现知识的逻辑顺序，揭示数学的内部关联。

需要注意的是，这个环节的设问一要精炼，不能用时过长;二要精准，抓住切入新知的时机，以有效引发学生探究新知的内驱力。

2.创设情境问题，步步追问，引导自主探究。

课的开始阶段，创设情境问题能集中学生注意力，吸引学生快速进入学习状态，一个贴近生活、贴近实际、学生熟悉的问题，更能诱发学生主动观察、联想，进而在问题的指引下，进入抽象、概括、数学化的过程。这样学生新知探究之路便成功开启，学生想学、乐学、主动学得积极情态得以激发。

需要注意的是，情境问题的设置一要重视利用教材提供的素材，二要研究图文内容编写的背景和意图，深入挖掘其教学价值，让学生在学习中体会数学的价值。

3.布局展延问题，层层递进，实现深度思维。

新知的展延阶段一般是课的重点和难点。设问时要根据具体内容，精心布局、层层推进，为学生的深入探究铺好台阶，发挥“GPS”的作用。

需要注意的是，这个环节中问题的解决，老师要放手。别林斯基说：“教学方法应该使学生自觉地掌握知识，使他们发展积极的思维”。让学生自己去寻求问题的正确解答，这种内需的力量有助于他们领会知识和掌握技巧，当他们尝到成功的乐趣后，对学习的热爱就是很自然的事了，而且持续的、积极的求知欲对他们一生的发展都具有重大意义。

4.设好小结问题，提炼整理，诱发继续探索。

课堂小结时，要改变以教师为主体陈述的总结方式。以上课例中我请同学们思考了两个问题。一是“今天你收获了什么？你觉得自己学得如何？”我鼓励学生采用多种形式的自主小结和自主评价：或小组讨论代表发言，或个人上台发言其他学生补充，最后是老师补充完善，及时评价、鼓励。二是“关于一次函数你还想知道哪些？”此问旨在引导学生基于本课的内容进行合理联想，为下一节的教学内容做好铺垫;同时通过类比同类知识的学习，以期获得相关的学习经验和方法;尤为重要的是延续学生饱满的学习热情、积极的思维状态。

需要注意的是，小结问题的解答主要以表述为主，体现学生的语言表达和概括能力，学生的回答不一定全面，所以课堂小结环节要留有一定的时间，让学生互相补充，在知识和思想方法两个层面充分总结，并对知识的延伸做好伏笔。

课堂中一串由浅入深、由表及里、由简到繁的有梯度的探索性问题，是学生目标达成的脚手架，能让课堂充满灵动、充满思维。学生在探求问题的过程中，学习的积极性得以调动，学习的动机水平得以提高，成功的机会得以创造，良好的意志品质得以培养，学习兴趣得以激发，学生也就始终处在深度学习之中。

（作者单位：无锡市后宅中学，江苏 无锡214145）