基于改进的CDKF锂电池SOC估计方法
张小利,王玥童,夏金松,张莹莹,2
(1合肥工业大学自动化工程学院;2可再生能源接入电网技术国家地方联合工程实验室,安徽合肥 230009)
近年来,锂离子电池凭借单体电压高、寿命长、无污染等特点广泛应用于新能源汽车、航空航天等领域[1-2]。为了更高效地管理电池,研究人员[3]提出建立电池管理系统(battery management system,BMS)的解决方案,其中电池荷电状态(state of charge,SOC)的准确估计是BMS的重要功能,可以为电池之间的均衡管理提供依据,进而延长锂电池的使用寿命。
针对卡尔曼滤波方法关于电池SOC 估计存在的问题,研究人员提出很多改进方法,其中扩展类型的卡尔曼滤波方法(extended Kalman filter,EKF)应用最多[4-5]。文献[6]建立了磷酸铁锂电池PNGV等效模型,基于EKF方法估计电池SOC值。文献[7]基于电池多模型辨识未知参数,联合库仑积分法和EKF 算法来估算SOC 值。EKF 算法虽然在工程上有一定应用,但该算法也存在一些不足,如EKF算法涉及到雅可比矩阵的计算,而该矩阵计算过程比较复杂,计算工作量很大,且对系统稳定性有一定影响。为了解决EKF存在的问题,文献[8]提出了中心差分卡尔曼滤波算法(central difference Kalman filter,CDKF),该算法不必计算雅可比矩阵,而是选择插值公式来表征非线性函数,这样处理减小了计算工作量。相比EKF算法,CDKF算法估计精度更高,但CDKF算法仍然无法回避非线性问题转化为线性问题的处理过程,这个过程势必产生线性误差,为继续提升估计精度,有必要对CDKF算法进一步改进。
本文建立二阶RC 电路单元模型作为锂电池等效模型,采用最小二乘参数辨识方法,辨识等效模型电阻和电容参数。在原CDKF算法中引入迭代滤波思想,使得观测信息不断迭代更新,基于LM 优化方法不断修正协方差矩阵,在此基础上提出一种改进的CDKF算法。后面分别在恒流放电和动态放电工况下对改进后的CDKF算法进行实验验证,并将预测结果与CDKF算法进行比较,结果表明改进后CDKF算法估计精度高于原算法,对初值误差收敛性也更好。
1 电池等效模型的建立
相比一阶阻容(RC)电路单元模型,二阶RC电路单元模型表征电池动态特性具有更高的估计精度,而三阶及以上RC 电路单元模型又过于复杂。综合衡量模型精度、复杂度,本文选择二阶RC 电路单元模型[9-10],利用该模型模拟充放电过程中锂电池的动态变化特性,二阶RC 电路模型结构如图1所示。该电池模型可以划分为三个部分:电压源、欧姆内阻、RC电路单元。UOC表示锂电池的开路电压,通常在锂电池较长时间静置后测量锂电池两个电极之间的电压来获得。R0为锂电池的欧姆内阻,表示锂电池内部电流回路中的等效纯电阻。两个RC 单元用来模拟电池的极化效应,表征放电结束后,锂电池静置期间电压突变后的电压渐变过程。
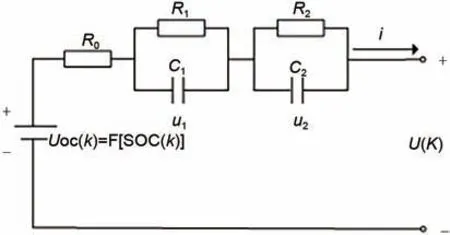
图1 二阶RC电路单元模型Fig.1 Second-order RC circuit unit model
由图1中二阶RC电路单元模型可得
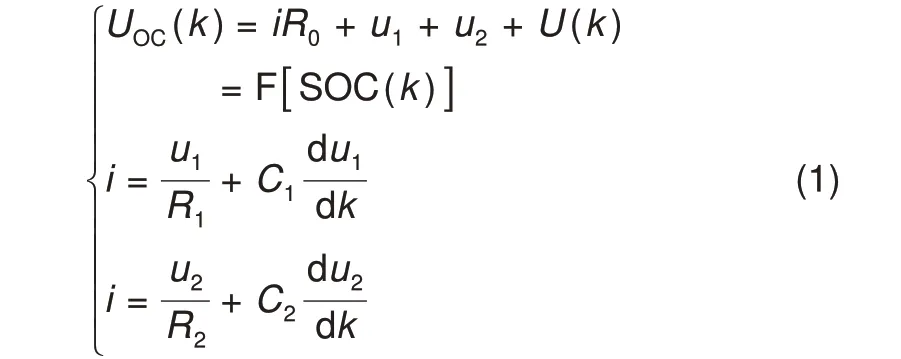
对于锂电池而言,k时刻电池SOC值为
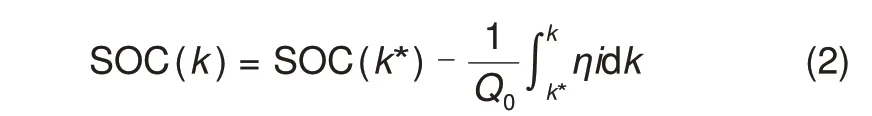
式中,k*为k的前一时刻;η为补偿系数;Q0为电池可用容量。
以锂电池荷电状态值SOCk、两个RC 单元的端电压u1,k和u2,k作为状态变量,Ik表示控制变量;Uk表示观测变量;v(k)表示测量噪声;w(k)表示过程噪声,设采样周期为T,综合式(1)和式(2)可得锂电池状态方程为
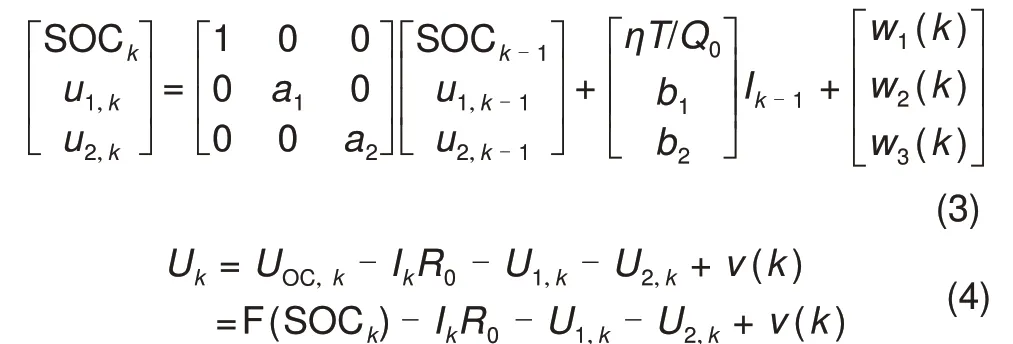
其中,a1、a2、b1、b2表示如下

根据二阶RC 电路单元模型和状态方程可以求得系统方程
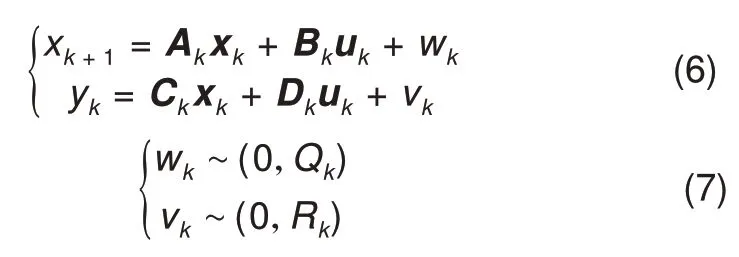
式中,Ak、Bk、Ck、Dk分别表示状态转移、输入、输出以及前馈矩阵;uk、xk分别表示控制变量和状态变量矩阵;wk、Qk分别为过程噪声及其协方差,vk、Rk分别为测量噪声及其协方差。
2 CDKF算法及其递推过程
CDKF 算法主要是基于Sterling 插值公式按中心差分方式描述非线性模型,该方法不必计算雅可比矩阵,不用对函数求偏导数,减小了计算工作量。中心差分形式代替泰勒公式展开形式的一阶、二阶导数项
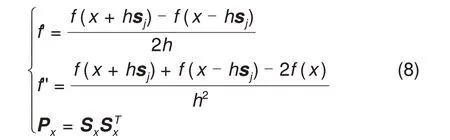
式中,h为中心差分步长,其取值大小影响逼近非线性函数的精度,之前的研究表明,对于高斯分布,h2值取3 时,可以达到最佳逼近状态[11]。Sx为协方差矩阵Px经Cholesky 分解得到的矩阵,sj为Sx矩阵第j列向量,和x有着相同的协方差且均值为零。
Sigma 点滤波过程为:首先选取若干采样点,采样点和状态变量两者的均值和协方差值均要相同,然后根据非线性函数计算采样点对应的函数值,最后利用采样点的函数值计算状态变量的均值及协方差值。
CDKF算法采用对称采样策略选取Sigma采样数据点,M维的状态变量需要采集2M+1 个采样数据点。由于采样数据点均值、协方差值需要同状态变量对应的取值一致,各个采样数据点对应的位置如下式所示
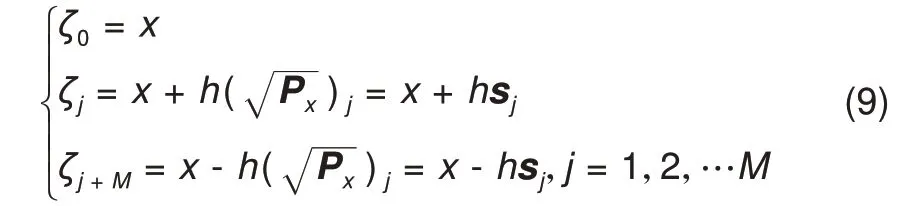
采样点ζj权重取值可由下式求得
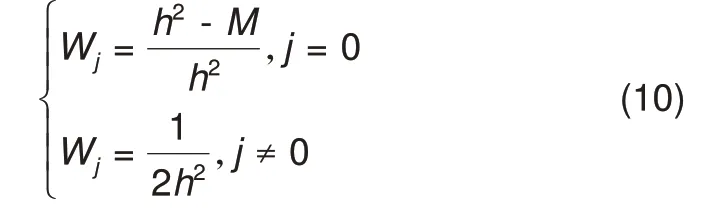
本文状态变量是[SOCk u1,k u2,k]T,故M取值为3。由式(10)可知对称采样权重取值只有两种,分别对应中心点和非中心点的权重大小,这表明其他非中心点具有同等重要性。
在Sterling 插值公式采取对称采样Sigma 点策略计算状态变量后验协方差和均值,即实现CDKF估算过程,其具体递推过程如下[12]。
①初始值,k=1。
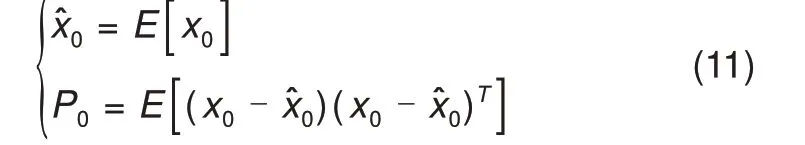
②构造2M+1维Sigma点
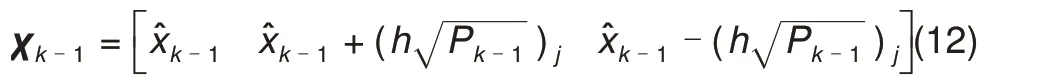
③时间更新
状态估计
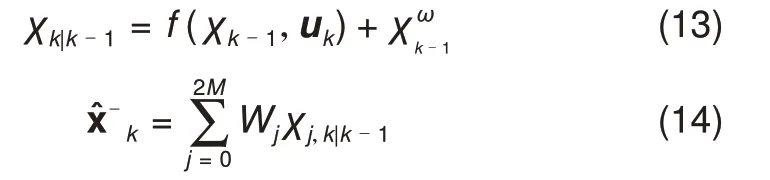
误差估计
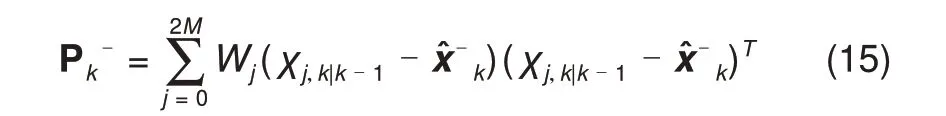
观测估计
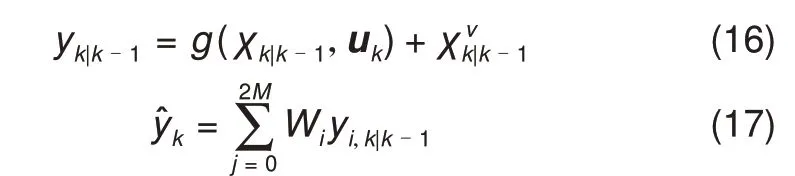
④测量更新
互协方差计算
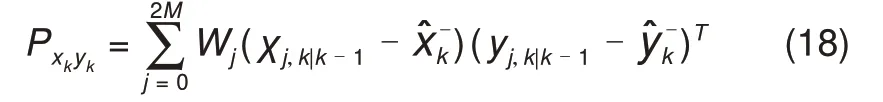
自协方差计算
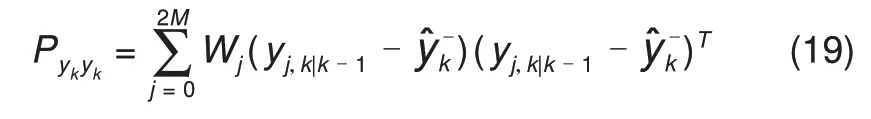
估计增益矩阵

状态估计测量更新
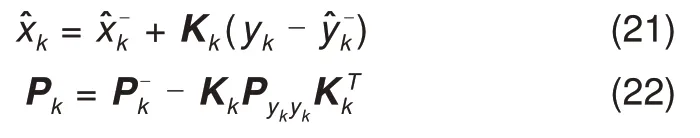
⑤当k=k+1时,重复步骤②~④。
3 改进的CDKF算法及其递推过程
式(21)中是以x̂-k为基准计算得到Kk和ŷ-k的值,相比于x̂-k,x̂k与实际值差异更小,若以x̂k为基准,对观测方程多次带入求解,求得状态估计值更接近实际值。对这个过程反复进行多次,也即把迭代思想引入进来,多次利用测量信息更新状态量估算值,进而减小锂电池SOC估计误差。
假设式(23)基准点为γj,测量更新值为γj+1,迭代方法可用下式表示
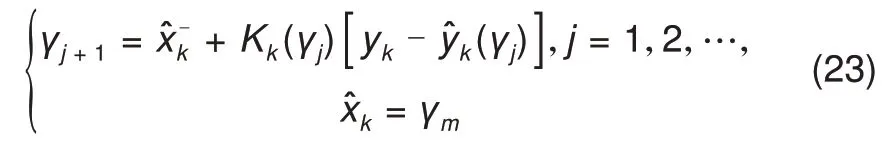
式中,j为迭代次数,γ1=为初始基准点。
迭代一次需要计算一次增益矩阵Kk和测量变量ŷk,当迭代次数等于m时,结束迭代过程,最后的输出结果即为最优估算值。
非线性系统符合局部线性化条件时,对于卡尔曼滤波,若代价函数M(xk)定义为

其更新迭代可认为是基于GN(Gauss-Newton)法迭代求解M(xk)极小值。但由于引入了线性误差,状态模型和观测信息不一定完全相同,因此仅能求解M(xk)非零极值,这等价于将GN 法解决小残差迭代优化问题。而GN法处理此类问题往往导致系统不稳定[13],进而影响SOC 估计精度。主要体现在观测更新迭代过程中,估计误差不能确保一致减少,即yk-不能确保一致减少,导致估测的协方差矩阵相比真实值偏小,没有很好利用观测信息。LM(Levenberg-Marquardt)法可以求得非线性最小化(局部最小)的数值解。此方法能够结合GN法和梯度下降法的优点,并改善两者的不足(如应用GN法时若不存在反矩阵或初值与局部极小值相距太远)。
故本文引入LM 方法,迭代过程中通过LM 方法中的参数μl对协方差矩阵不断进行修正,从而确保系统的稳定性,提高SOC估计精度。
LM 方法利用阻尼参数因子μl对协方差矩阵进行修正,μl的取值规则前人已有研究[14]。经过修正的协方差矩阵如下式

改进后的CDKF 算法中,基于LM 修正后步骤④测量更新过程如下所示

4 模型参数辨识
首先完成OCV-SOC 标定实验,确定OCV 和SOC之间的函数关系表达式,然后在OCV-SOC函数关系表达式基础上,再结合最小二乘参数辨识方法,辨识等效模型电阻和电容参数。
4.1 OCV-SOC标定实验
选用Arbin 电池充放电测试系统对锂电池进行充放电实验,该系统具有上位机测试软件(MITS Pro),可以在该软件上编程控制选择充放电模式、设置充放电测试截止条件等,ARBIN电池充放电测试系统如图2 所示,锂电池主要参数指标如表1 所示。该实验是在25 ℃恒温条件下展开进行的,以0.2C 放电倍率对锂电池进行恒流间歇放电实验,从而得到对应的开路电压-荷电状态(OCV-SOC)曲线,OCV-SOC曲线如图3所示。

图2 Arbin电池充放电测试系统Fig.2 The Arbin battery charge and discharge test equipment

表1 锂电池主要参数指标Table 1 Main parameters of lithium battery
对该曲线进行5阶多项式函数拟合,拟合得到的OCV-SOC具体函数表达式如式(36)所示。
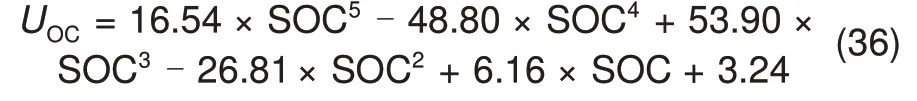
4.2 参数辨识
对于图1 中的电池等效模型,需要辨识R0、R1、R2、C1、C2等参数。基于含遗忘因子的最小二乘法,根据自定义工况完成对模型未知参数的在线辨识。二阶RC 电路模型在自定义工况下的辨识结果如图4所示。由图4可知,在参数辨识初始阶段,待辨识参数值波动较大,这主要由于初始化参数初值设置不准确所致,后面随着时间的延长,各参数均收敛于某一固定值。
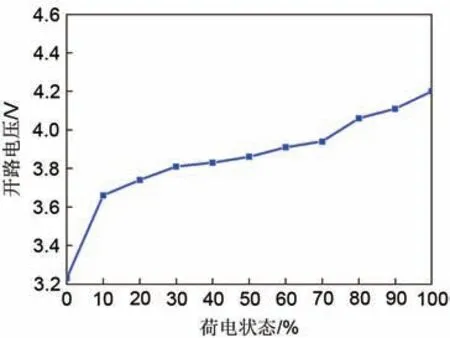
图3 间歇放电OCV-SOC曲线Fig.3 Intermittent discharge OCV-SOC curve
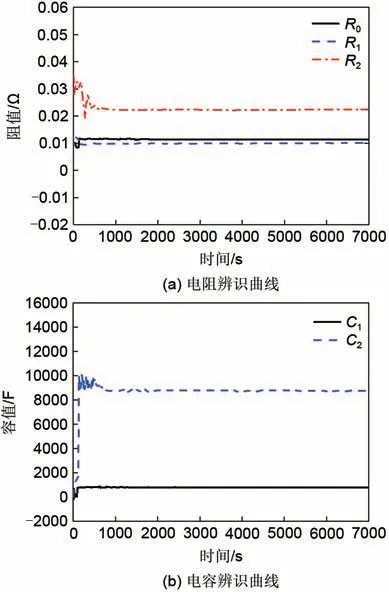
图4 参数辨识曲线Fig.4 Parameter identification curves
4.3 模型验证
得到模型参数辨识结果之后,需要对电池模型进行精度验证,这里主要基于HPPC实验验证模型的精度。其中,SOC 初始值为80%,电流大小取1 C,实验的电流波形如图5所示,图6是实际电压和模型估计电压波形对比图。
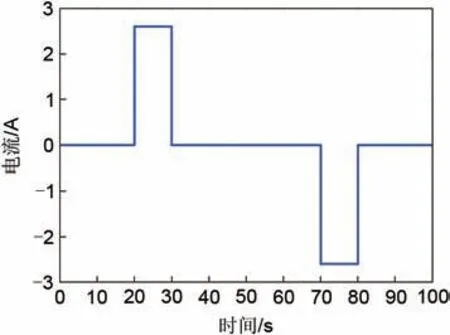
图5 HPPC电流波形Fig.5 HPPC current waveform
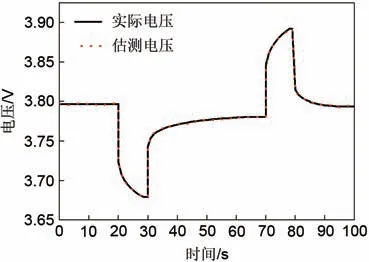
图6 实际电压和估测电压对比图Fig.6 Comparison of actual voltage and estimated voltage
由图6可知,电流发生突变时,模型估测电压波形可以很好地追踪电池实际电压,该等效模型可用于后续对SOC估计算法的比较和验证。
5 不同工况下SOC估计验证
对电池模型验证之后需要验证改进后的CDKF算法估算效果。在Matlab 中编写程序分别实现CDKF算法和改进后的CDKF算法,选择在恒流放电,动态放电工况下对算法估计准确性进行验证,针对每种工况设置不同的SOC 初始值,对算法收敛性进行验证。
5.1 恒流放电工况
以0.5 C 恒流放电工况下验证算法估计荷电状态准确性,电池从全满状态下(SOC=1)恒流放电,为了便于验证电池SOC估算精度,将电池SOC初值设为1,放电总时间7200 s,采样周期为1 s。
图7表示恒流工况下CDKF算法改进前后对电压的估计结果,图8 是CDKF 算法和改进的CDKF算法估计电压的误差对比结果。由图7可知,基于二阶RC 电路模型CDKF 算法和改进的CDKF 算法都可以获得较准确的估计结果。由图8 可得CDKF算法最大估算误差为1.77%,改进后的CDKF算法最大估算误差为1.27%,改进后的CDKF算法取得更好的估计效果。
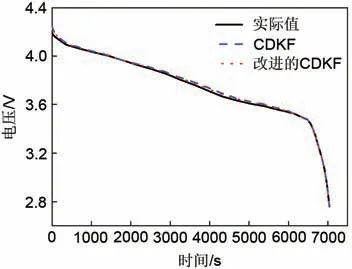
图7 恒流工况下时电压随时间的变化关系Fig.7 The relationship of voltage with time under constant current condition

图8 恒流工况下电压估算误差对比曲线Fig.8 Estimation error of voltage comparison curves under constant current condition
图9表示荷电状态已知时,即荷电状态初值为1时的恒流放电实验的估计结果,图10是CDKF算法和改进的CDKF算法荷电状态的估计误差对比结果。由图9 可知,基于二阶RC 电路模型CDKF 算法和改进的CDKF算法都可以获得较准确的估计结果。恒流工况下,电流波动很小,系统噪声相对较小,由图10 可得CDKF 算法最大估算误差为2.08%,改进后的CDKF 算法最大估算误差为1.38%,精度提高了0.7%。相比较CDKF 算法,改进后的CDKF算法的估计值更接近实际值,估算过程平稳,取得更好的估计效果。
综合恒流工况下电压和SOC估算结果,求得算法改进前后误差值,具体数据如表2所示,主要包括均方根误差(RMSE)和平均绝对误差(MAE)。由表2中相关数据可知,在RMSE、MAE 方面数据可知,改进的CDKF算法估算偏差更小,更具有优势。
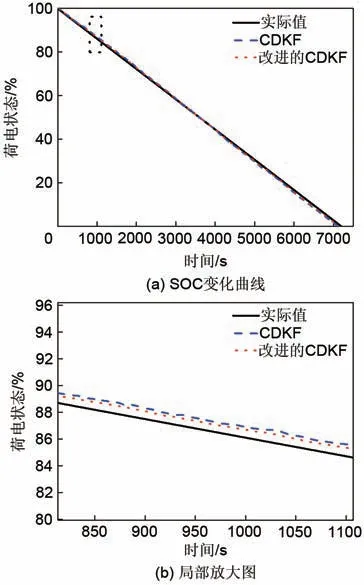
图9 恒流工况下SOC随时间的变化关系Fig.9 The relationship of SOC with time under constant current condition
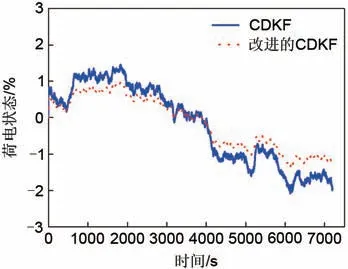
图10 SOC估算误差对比曲线Fig.10 Estimation error of SOC comparison curves
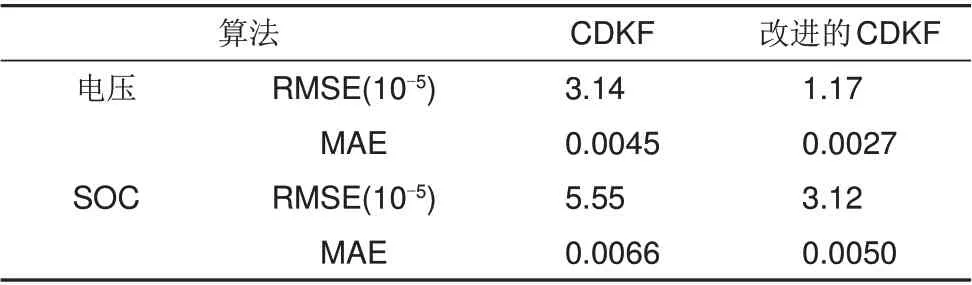
表2 恒流工况下电压和SOC估计误差比较Table 2 Estimation error of Voltage and SOC comparison under constant current condition
5.2 动态工况
电动汽车行驶中的环境复杂多样,动态工况模拟实际电动汽车运行情况,不是单一的充电或放电过程,包含充电和放电的交替过程,在动态工况下充放电电流是不断变化的。图11 表示动态工况下CDKF 算法改进前后对电压的估计结果,图12 为CDKF算法和改进的CDKF算法电压的估计误差对比结果。由图12 可得CDKF 算法最大估算误差为2.69%,改进后的CDKF 算法最大估算误差为2.06%,改进后的CDKF 算法取得更好的估计效果。
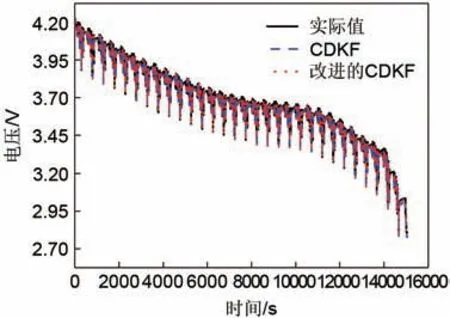
图11 动态工况下时电压随时间的变化关系Fig.11 The relationship of voltage with time under dynamic condition
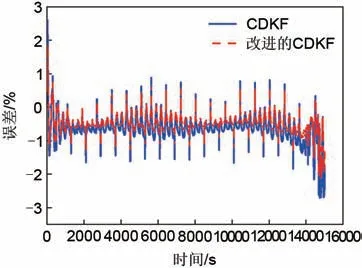
图12 动态工况下时电压估算误差对比曲线Fig.12 Estimation error of voltage comparison curves under dynamic condition
在动态工况实验中,已知荷电状态初始值时SOC估计结果如图13所示,图14为CDKF算法和改进的CDKF算法在动态工况下荷电状态的估计误差对比结果。由图14 可得CDKF 算法的最大估计误差为2.79%,改进的CDKF算法最大估计误差为1.63%,精度提高了1.16%,由此可知改进后的CDKF 算法估计结果更接近真实值,估算误差更小,表明在变电流情况下,该算法仍然具有较高的准确度。
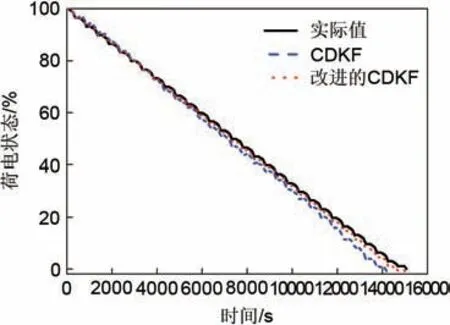
图13 动态工况下SOC随时间的变化关系Fig.13 The relationship of SOC with time under dynamic condition

图14 动态工况下SOC估算误差对比曲线Fig.14 Estimation error of SOC comparison curves under dynamic condition
综合动态工况下电压和SOC估算结果,求得算法改进前后误差值,具体数据如表3所示。由表3中数据可知,在RMSE、MAE 方面算法改进后的数值均小于算法改进前数值,表明了改进后CDKF估算效果更好。
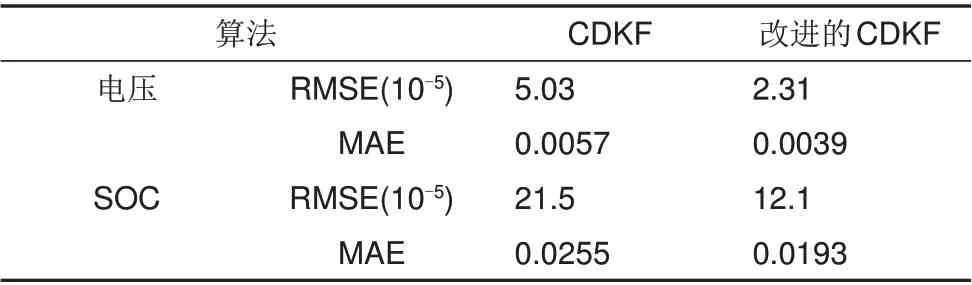
表3 动态工况下电压和SOC估计误差比较Table 3 Estimation error of Voltage and SOC comparison under dynamic condition
5.3 算法鲁棒性比较
相比库仑积分法,卡尔曼滤波方法优势在于即使初始值设置不同也可以自动跟踪到真实值附近,但跟踪速度是不确定的。这里仍以恒流工况和动态工况为例,设定SOC 初始值为非真实初始值,这里SOC值设置为80%。
图15 表示恒流工况和动态工况下电池荷电状态初始状态未知时SOC 随时间的变化关系曲线。从图中可以看出改进的CDKF 算法从SOC 初始值跟踪到实际值的时间更短,收敛速度比CDKF算法快,说明改进的CDKF算法修正能力更强,具有更好的鲁棒性,这也从侧面说明了改进后的CDKF算法精度更高。
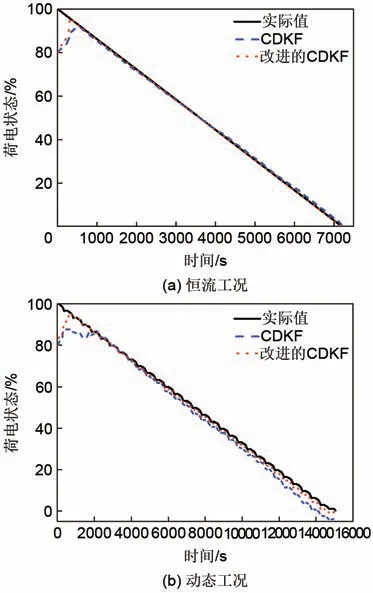
图15 初始状态未知时SOC随时间的变化关系Fig.15 The relationship of SOC with time when the initial state is unknown
6 结论
针对中心差分卡尔曼滤波算法(CDKF)存在较大线性误差问题,本文提出一种改进的CDKF 算法。在原算法中引入迭代滤波思想,多次利用测量信息更新状态量估算值,使得观测信息不断迭代更新,基于LM 优化方法不断修正协方差矩阵,有效减小了线性误差。在恒流工况和动态工况下对CDKF算法和改进后的CDKF算法进行验证。对于电池SOC 值估计,在恒流工况下,CDKF 算法估计最大误差是2.08%,改进后的CDKF算法最大估计误差为1.38%,精度提高了0.7%;在动态工况下,CDKF 算法估计最大误差是2.79%,改进后的CDKF 算法最大估计误差为1.63%,精度提高了1.16%,两种工况下改进后的算法估算精度都高于CDKF 算法,在动态工况下表现效果更明显。此外,通过不同的荷电状态初始值的设定,对两种算法鲁棒性进行比较,结果表明改进后的CDKF算法鲁棒性高于原CDKF算法,综上所述,经过改进的CDKF 算法在收敛速度和估计准确度方面更有优势,具有更好的应用前景。

