兼顾储能系统热管理与电池寿命的可再生能源储能电站经济调度

张 超，康 慨，卢 胜，覃新宇，黄彦博，李正天

（1湖北省电力勘测设计院有限公司，湖北武汉 430040；2强电磁工程与新技术国家重点实验室（华中科技大学），湖北武汉 430074）

为满足行业政策及技术规范要求，各新能源场站逐步建立配套储能电站以提升跟踪计划出力与平抑波动的能力。但是，运行经济性是衡量储能电站性能的重要指标之一，储能与风/光等新能源如何协调出力，达到优化运行的目标，需要相应的经济优化调度策略予以保障，这也是当前电力行业的研究热点和实际工程需求。

当前，关于光储、风储联合电站的优化调度策略的研究颇多。文献[1]推导了计算蓄电池放电损耗的数学模型，并基于拉格朗日松弛和内点法的动态规划用于考虑放电损耗的调度模型中。文献[2]基于电池放电损耗模型，进一步考虑了大规模储能电池面临的充放电路径选择问题，提出了精细化储能电池功率分配策略。文献[3]以储能电池功率分配策略为基础，建立计及温度对电池损耗成本的LLI-LAM复合循环容量损失模型，并得出储能电站经济优化调度策略。以上文献在储能电站经济调度方面已经层层深入地进行诸多探索，却忽略了利用电站温度调节系统主动调节电池运行温度以降低电池损耗成本，进而优化储能电站调度经济性的举措。

本文针对上述存在的问题，拟以储能电站调度成本最低为目标，研究提出考虑储能电站热管理以及电池温度容量关系的电站经济调度策略。该调度策略在计及电池全寿命周期成本的基础上，还综合考虑了构成储能系统的化学电池容量随温度的变化，及该效应带来的电池寿命损耗成本影响，构建了利用温度调节系统主动降低电池损耗的调度模型。为满足日内实时调度对求解速度以及求解精度的应用要求，以分片McCormick 对双线性项进行线性化，并利用Gurobi 工具进行求解，优化调度结果有望确保电站经济运行。最后针对常用调度策略与所提调度策略进行了对比分析，验证了其有效性和优越性。

1 考虑热管理的可再生能源联合储能电站优化调度模型

1.1 可再生能源联合储能电站发电系统

一般可再生能源联合储能电站发电系统包括光伏/风电等可再生电源、功率调度系统、温度监管系统以及多个电池系统等，其结构如图1所示。

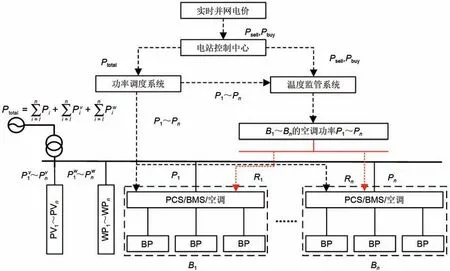
图1 可再生能源联合储能电站结构示意图Fig.1 Schematic diagram of the structure of renewable energy joint storage power plant

图1中，Psell表示实时并网电价；Ptotal表示全站总功率；B1～Bn表示n个独立的集装箱式电池系统；P1～Pn与R1～Rn分别表示各独立电池系统电池功率与空调功率，Pv1～Pvn表示PV1～PVn光伏电站出力，Pw1～Pwn表示WP1～WPn风电场出力。其中，各独立电池系统分别含储能变流器(PCS)、电池管理系统(BMS)、电池组以及电池温度调节系统。温度调节系统根据当前环境、电池物理特性以及功率调度情况调节电池组的运行环境温度。储能电站控制中心依据电网发布的实时并网电价进行储能电站内功率调度，温度监管系统综合考虑电池运行效率、当前环境、空调费用以及电池物理特性控制各独立电池系统的产/排热功率。

分析储能电站各系统可知其运行成本主要分为人工成本与设备运行及损耗费用。针对占比较大的设备运行及损耗费用进行分析，可以发现温度调节系统产/排热所需电能费用以及电池充放电的寿命损耗费用需要具有较高优化价值。

在上述联合发电系统中，电池会带来热量耗散，从而导致温度升高。然而，电池损耗成本与储能电池容量直接相关，储能电池容量对环境温度十分敏感。因此，需要将集装箱内的电池运行环境温度，与电池实时功率联合考虑，实现考虑电池寿命损耗成本和温度调节系统费用的联合经济调度。目前，此方面的研究成果寥寥。实际上，集装箱式储能箱体内部温度由热负荷和制冷量两部分决定。其中热负荷包含太阳辐射功率、箱内电器热功率、电池发热功率以及温度调节系统产热功率等，制冷量则仅为温度调节系统制冷功率。为实现上述电池寿命损耗成本和温度调节系统费用联合优化，本文基于电池温度容量关系，建立箱式储能电站热负荷模型，并将其应用于考虑电池寿命损耗成本的经济调度策略。

1.2 箱式电池模组热功率平衡模型

为实时计算并预测电池运行的环境温度，需要综合考虑箱式储能电池模组内各部分产/排热功率，由此得到计及电池损耗产热功率、产热箱内外热传导功率、箱内电器热功率以及空调产/排热功率的热功率平衡公式如式(1)所示。

式中，QB表示电池损耗产生热功率；QEV表示集装箱与外界热传导的热功率；QG表示集装箱内计算机及照明设备等散发的热功率，通常取一额定数值(3 kW)；QA为空调产/排热功率。

太阳直接照射集装箱表面会引起箱表面的额外温升。理论上集装箱的4个侧面以及顶面都存在该效应，但由于太阳辐射照射侧面的时间较短且阳光与侧面夹角较小，相对太阳直射的顶部温升效应可以忽略，因此针对集装箱顶部，可由式(2)计算该温升效应[4]。

式中，TO为箱外空气温度；γ为箱顶对太阳辐射的吸收系数；I为箱顶法线方向太阳辐射强度；Tto为集装箱顶部温度，α0为空气与箱表面传热系数，一般取为5。

在考虑太阳热辐射产生的温升后，可以分顶部和侧面计算QEV，如式(3)～(5)所示

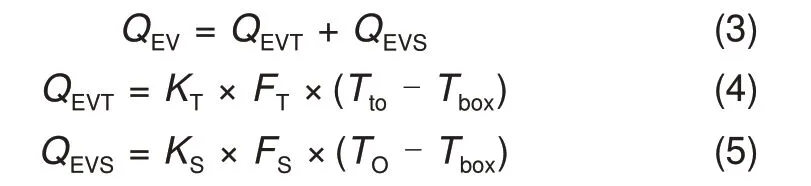
式中，QEVT与QEVS分别表示由集装箱顶部与侧面传导的热功率；KT与KS分别表示集装箱顶面与侧面传热系数，FT与FS分别表示集装箱顶面与侧面面积；Tbox表示集装箱内温度。

由于电池充放电时效率小于1，损耗一般以热量形式向外界环境散发，因此QB可由式(6)计算

式中，η为电池充放电效率；Pcha与Pdischa分别表示电池充、放电功率。

此外，温度管理系统会对温度进行调节，从而产生或者排除热量，如式(7)所示

式中，PA表示温度管理系统功率；h表示温度调节系数。通过上述式(1)～(7)即可在线实时预测箱内温度，从而为联合经济调度提供调节依据。

1.3 计及储能寿命的充放电损耗模型

为了实现兼顾电池寿命损耗成本的经济调度，在考虑上述温度预测外，由于充放电还会损耗电池寿命，对经济调度会带来不可忽略的影响。所以在调度决策过程中，还需充分计及电池寿命损耗。为此，必须构建合理的充放电损耗模型。

以锂离子电池为例，在循环使用的过程中，锂离子活性损耗与电极表面副反应等原因降低电池的充放电能力，据此可以考量电池的充放电损耗成本[5-6]。如式(8)所示，循环次数随放电深度变化，因此不同放电深度的电池损耗不同。进一步将不同放电深度的循环统一折算可以得到对应的等效全循环次数，如式(9)所示。由此可以计算各时段内电池充放电损耗成本，如式(10)所示。

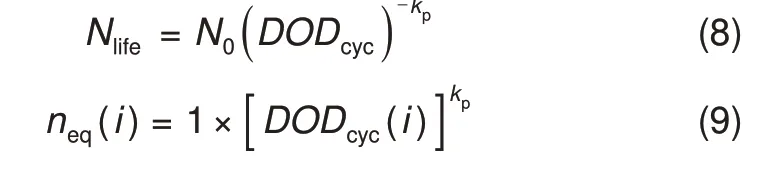
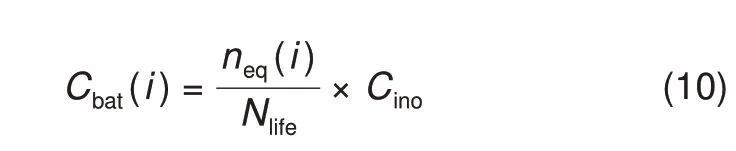
式中，Nlife表示电池全寿命周期可循环次数；N0表示电池以最大放电深度充放电可循环次数，DODcyc为电池运行时充放电深度；kp为拟合参数；neq(i)表示i时刻对应的等效全循环次数；Cino表示电池建设成本；Cbat(i)表示对应时段充放电损耗成本。

2 兼顾温度调节成本与电池寿命损耗的经济调度策略

2.1 经济调度目标函数

目前新能源场站的储能容量配置的出发点均是在满足并网运行要求的前提下，实现总体经济性最优。目前新能源场站应用储能的场景繁多，本文考虑平抑出力以及充分利用分时电价的场景。在该场景下，基于经济性最优原则，提出如下目标函数

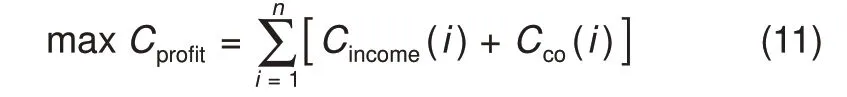
式中，Cprofit表示运行日净收益；Cincome(i)表示第i个时段内各项收益；Cco(i)表示i时刻电站成本，二者计算式如式(12)～(13)所示

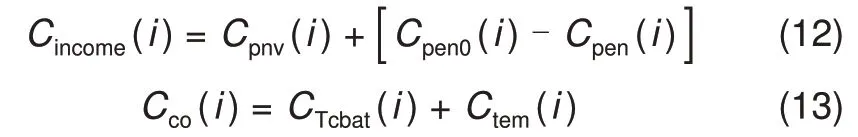
式中，Cpen(i)为i时刻考核电量引起的罚款；Cpen0(i)表示i时刻无储能时电站所受惩罚金额；Cpnv(i)表示i时刻的峰谷套利收益；CTcbat(i)为i时刻经电池温度容量关系修正的电池寿命损耗成本(将于本节给出)；Ctem(i)为i时刻温度调节成本。以上公式建立了包含温度调节费用以及经修正的电池寿命损耗成本的收益计算模型。

（1） 跟踪计划出力的收益

由于风电、光伏为代表的可再生能源出力波动剧烈、发电不稳定，电力系统易受影响而产生运行安全性问题。因此，国内华中区域等已出台相关文件[7]对可再生能源出力进行约束与考核。为适应新规则对可再生能源场站的约束，本文利用储能系统以平抑可再生能源出力波动，保证电网运行的稳定性。由于各种储能单元特性不同，适应场景也由此不同，为进一步增强储能电站经济性，需要综合利用性能型与经济型储能单元。由于现有储能装置运行成本高昂，需要在保证平抑光伏电站波动性、提高电站经济性基础上，降低储能运行成本。为计及该问题，该部分以华中地区数据为例，建立光伏电站考核金额的模型。收益模型如式(14)～(15)所示

式中，PMi为i时刻的实际功率；PPi为日前功率预测值；Ccap为新能源电站的可用容量；n为发电时段样本个数；PN为新能源电站的额定容量；λ为预测准确率，Ppenalty为考核电量单价，在λ大于85%时不计算考核电量。由以上公式建立了新能源电站出力的考核费用，而通过储能电站减少的考核费用即可记为储能系统的收益。

（2） 分时电价收益

当前国内大部分地区的新能源联合储能电站难以直接参与分时电价套利，但通过负荷曲线与出力曲线变化趋势不匹配时产生电价的波动，可以调节负荷与出力曲线，实现提高新能源消纳与降低电力成本的目的。本文以美国电力市场为背景，将场站侧电价对应节点边际电价(LMP)，得到每小时的分时电价。储能电站可以在电价低谷时吸纳新能源场站出力，电价高峰时再售出，同时实现了场站盈利与负荷-出力曲线的匹配。

其收益计算公式如式(16)～(18)所示

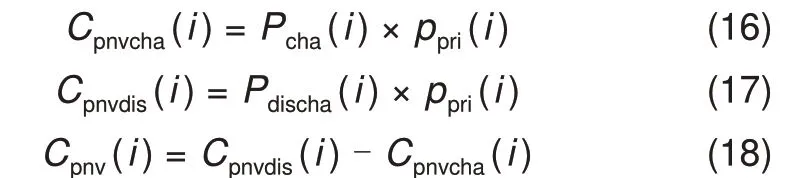
式中，Cpnvcha(i)为i时刻储能电站从新能源场站吸纳电能所需成本；Cpnvdis(i)为i时刻储能电站售电盈利；ppri(i)为i时刻并网电价；Cpnv(i)为i时刻从储能电站充分利用分时电价收益。

（3） 热功率成本计算

温度调节系统的成本计算如式(19)～(20)所示

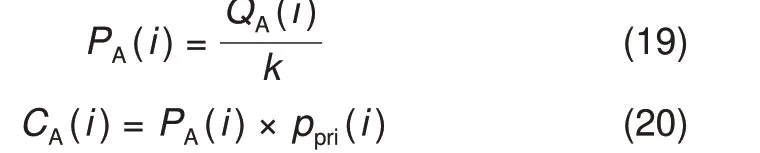
式中，PA(i)表示i时刻温度调节系统所需空调电功率；k为产/排热功率与电功率比例，一般取为定值2.6；Ctem(i)为i时刻温度调节系统费用。

（4） 经温度容量关系修正的电池寿命损耗成本

电池放电容量随温度而变化[8]，但是高、低温时容量衰减原因不尽相同。文献[9]讨论了不同温度下放电容量衰减量以及衰减原因，得知高温下容量衰减的主要原因为正负极材料的活性增强，导致材料性能不稳定，因而为不可逆损耗；而低温下容量衰减的主要原因为离子活性的暂时降低，导致阻抗增大，容量减小，因而为可逆损耗。基于容量衰减的不同原因，限制电池最高温度为电池容量最大对应的温度。与此同时由文献[10]可知，当温度低于-10 ℃时，容量衰减过于明显，无法正常发挥功能，依此限制电池最低温度为-10 ℃。温度在允许区间变化时对应放电容量随之变化，其函数关系可由厂商提供，如图2所示。

图2 铅炭电池温度容量关系Fig.2 Temperature capacity relationship of lead carbon battery

分析图2 发现曲线可由式(21)进行拟合，对应可信度大于0.95。

式中，Tcap(t)表示温度为t℃电池的放电容量，t表示此时电池温度，[p3,p2,p1,p0]为拟合系数，即[5.331×10-4,-2.55×10-2,0.706,89.64]。

由此可以计算电池的关联温度实时放电容量，得到对应损耗，依此可知计及温度变化的电池损耗成本，如式(22)所示

式中，CTcbat(t,i)即为计及温度对放电容量影响的电池寿命损耗成本。

2.2 经济调度约束条件

可再生能源场站联合储能系统运行约束

式中，Ppv(i)为i时刻光伏电站实际出力；Pschedule(i)，Pvsell(i)为i时刻峰谷套利售电功率；Pcha(i)与Pdischa(i)分别为i时刻储能电池放、充电功率；Pab(i)为i时刻电站弃电功率；PN为电池额定功率；Ssoc(i)为i时刻电池电量；EU与L分别为电池电量上下限。式(23)建立了考虑储能系统及新能源场站的功率平衡。式(24)～(26)建立了储能电站的功率约束及容量约束。式(27)由第i+1个时刻以及第i个时刻得到了放电深度。

3 模型求解

上述调度策略模型的求解中存在两类非线性元素，一类为电池温度容量的非线性关系，另一类为式(22)。应用差分进化等智能算法虽然可以进行求解，但是其一难以满足调度策略的求解速度要求，其二难以保障所求解为最优解。为此，本文初步考虑第一类非线性元素以分段线性化处理，第二类非线性元素先转化为双线性项后利用精细化McCormick方案进行线性化。最后利用Gurobi求解线性问题。

（1） 将函数Tcap(t)取为倒函数Dc(t)后，进行分段线性化

针对电池温度容量的非线性关系，以铅炭电池放电容量与温度的关系为例，其函数取倒后的分段线性化过程如图3所示。函数取倒见式(28)。

图3 函数分段线性化示意图Fig.3 Schematic diagram of segmented linearization of a function

其温度容量的倒函数曲线表达式为

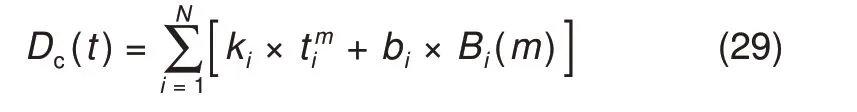
其中，各变量约束如式(30)～(33)所示

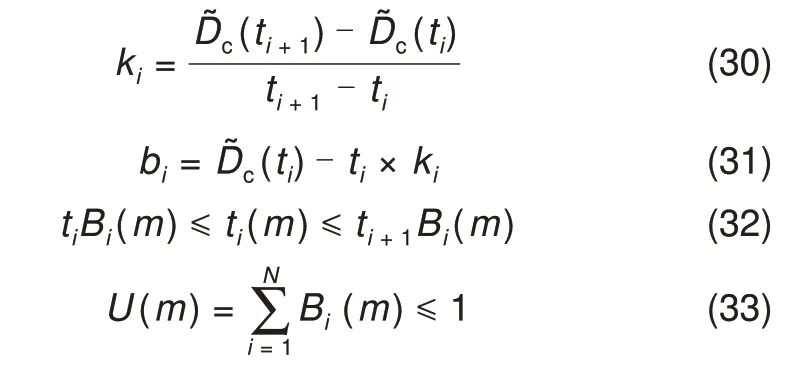
式中，D͂c(t)为电池温度容量倒函数；Dc(t)为温度容量倒函数的线性化函数；ki表示线性分段函数第i段斜率；bi为第i段的等效截距；ti为第i个分段点；t1和tN+1分别为电池的最低工作温度与最高工作温度，ti(m)表示第m个时刻的第i段温度；Bi(m)为标志位，表示电池的温度状态。

（2） McCormick线性化方法

针对式(22)中非线性因素，参考小节（1）可将式(22)变化为式(34)

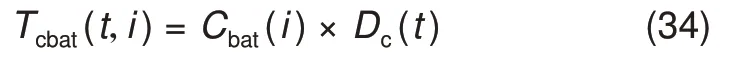
由此将非常规非线性元素变为较易处理的双线性项，但仍不能利用线性求解器直接求解，为此，利用McCormick方法对此进行处理，可将式(34)转化为如下约束

4 算例分析

本文对采用铅炭电池(advanced lead-carbon，ALC)和磷酸铁锂电池(LiFePO4，LFP)的混合储能系统的储能电站进行经济调度，价格源于《2020储能产业应用研究报告》，其中铅炭电池成本为1160元/(kW·h)，磷酸铁锂电池成本为2280元/(kW·h)，且充放电倍率分别为0.25 C 与1 C。上网电价参考文献[11]，如图4所示。

图4 典型场景的并网电价Fig.4 Grid-connected tariffs for typical scenarios

利用同步回代削减技术，分别由光伏电站与风电站得到一年内两个典型场景(场景1为光伏，场景2为风电)，如图5所示。

依据2.1节所提方案对计及DOD与总转移能量关系的电池寿命损耗模型进行线性化操作，分别得到铅炭电池与磷酸铁锂电池DOD 与寿命损耗的线性化关系如图6所示。

图5 新能源场站环境温度、太阳辐射强度与出力典型场景Fig.5 Typical scenarios of ambient temperature,solar radiation intensity and power output of new energy field stations

图6 电池总转移能量与DOD关系Fig.6 Total cell transfer energy versus DOD

同样地，对电池温度与容量模型线性化，得到 铅炭电池与磷酸铁锂电池温度容量模型见图7。

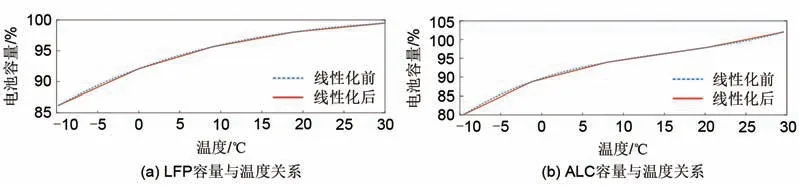
图7 电池温度与容量关系Fig.7 Relationship between battery temperature and capacity

4.1 考虑温度-容量关系的经济调度策略对比分析

为分析温度容量模型在储能电站经济调度中的应用效果，制定如下方案在不同场景中进行对比分析。

方案一：引用文献[12]的经济调度模型，该模型主要考虑了功率平衡、储能荷电状态约束以及电池寿命损耗，采用基于拉格朗日松弛与内点法的动态规划法求解模型。

图8 典型场景1的日内电池SOC、温度及损耗成本Fig.8 Intraday battery SOC,temperature and loss costs for typical scenario one

方案二：考虑电池温度容量关系的经济调度方案。

在如下场景下分别进行对比分析。

场景1：国内某50MW光伏电厂典型日；

场景2：丹麦某风电场实际数据典型日；

不同方案下电站SOC、温度及损耗成本与时间的关系如图8所示。

首先针对典型场景一进行分析，可以发现方案一中，铅炭电池与磷酸铁锂电池运行温度均处于安全限度内的较高水平，实现电池在安全温度内循环充放电的同时利用较高的温差达到了良好的自然散热效果。但是并未考虑温度容量关系。此外，结合电池损耗与SOC 的对比中可以看出，上午8：00—9：00，两个方案下LFP 的DOD 基本一致，但方案一的电池损耗较大。并且方案二能灵活调节电池温度，在电池充放电不频繁时采取更为经济的温度调节措施。

图9 典型场景2的日内电池SOC、温度及损耗成本Fig.9 Intraday battery SOC,temperature and loss costs for typical scenario two

而针对典型场景二分析可以发现，不考虑电池温度容量关系的方案一能够将电池温度维持在最低温度之上，但是电池充放电时的温度仍然较低，因虽然此温度调节系统成本较低，但是寿命损耗成本大大增大，降低了调度方案的经济性。相较而言，考虑电池温度容量关系的方案二在电池充放电时能够提供适宜电池充放电的环境温度，提高电池的充放电效率。在充放电速率较低时刻，为降低系统温度调节费用，将仅提供保障安全的电池运行温度。由此可知，方案二在兼顾温度调节系统功耗的同时也保障了电池充放电时处在适宜温度。

进一步分析可得储能电站的日净利润及电池寿命损耗成本，如表1所示。

综合分析可知，未考虑温度容量关系的调度方案虽然能根据天气实现储能电站的安全稳定运行，但难以保障电池在理想温度进行充放电。而综合电池温度容量关系的调度策略，能合理调节电站温度，明显降低电池寿命损耗，提高电站总体经济性。

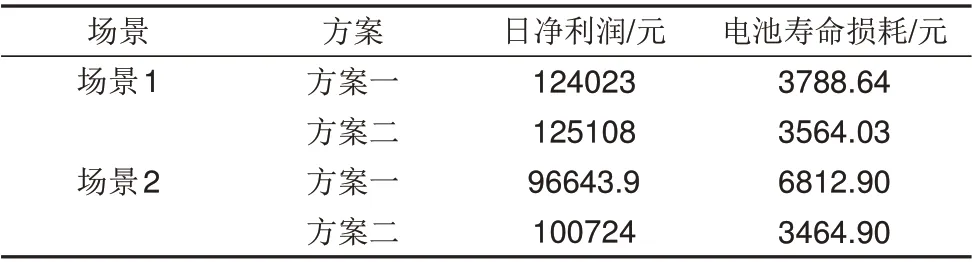
表1 储能电站日净利润与电池寿命损耗分析Table 1 Analysis of net profit and battery life loss in energy storage plants

4.2 考虑并网电价波动的模型分析

新能源场站分时并网电价与电力系统各运行时段的平均边际成本、新能源发电场站与火电厂实际出力以及用户负荷特性等因素有关，因此分时并网电价波动性较大。而分时电价作为日前经济调度需要考虑的重要因素，其波动性将直接影响生成的调度方案。在场景1中考虑并网电价的不确定性，将风、光出力的综合误差视为随机误差，以X～N(1,0.1)作为文献[11]所提上网电价的系数进行数据扩增。针对获得的30000种场景进行仿真分析，得到方案二下电站SOC、损耗成本及温度与时间的关系如图10所示。

图10 场景1考虑并网电价波动的日内电池SOC、损耗成本及温度Fig.10 Intraday battery SOC,loss costs and temperature considering fluctuations in electricity prices in scenario 1

图10中ALC包络线与LFC包络线表示ALC与LFC 日内电池SOC、损耗成本及温度的上下限，各部分透明线表示电池在各场景中实际运行情况，且颜色越深表示叠加的情况越多。分析图10 发现ALC在各场景下日转移能量均少于LFC，表明LFC单位转移能量成本低于ALC且在分时电价场景下盈利能力更强。针对图10 内LFC 的运行状况分析，可以发现8—10 时与12—18 时不同电价场景下电池运行情况差别较大。究其原因，一方面电池温度十分适宜于电池充放电；另一方面表明LFC储能系统对该时段电价十分敏感，可以有效针对电价波动调整调度方案。此外，在各电价不同的场景下，ALC 与LFC 充放电功率大小与电池温度依然存在较强耦合关系，若需实现大功率充放电则必须保证电池温度较为适宜以降低电池寿命损耗成本。

将以上并网电价数据应用于场景2，可以得到方案二下电站SOC、损耗成本及温度与时间的关系如图11所示。

图11 场景2考虑并网电价波动的日内电池SOC、损耗成本及温度Fig.11 Intraday battery SOC,loss costs and temperature considering fluctuations in electricity prices inscenario 2

与场景1不同，由于较低的环境温度将提高电池温度调节成本，场景2中温度调节系统仅在电池充放电能量较大时段主动升高电池运行温度。对比图10 与图11 分析可以发现，风电场因其本身出力波动相较光伏电厂更大，平抑波动需占用较高比例的储能资源，使得储能系统对于并网电价敏感性更高。

为验证本文所提考虑温度容量关系调度策略的有效性，进一步设置如下方案。

对比方案一：考虑温度容量关系与分时电价波动的光伏电站运行方案。

对比方案二：不考虑温度容量关系而考虑分时电价波动的光伏电站运行方案。

对比方案三：考虑温度容量关系与分时电价波动的风电站运行方案。

对比方案四：不考虑温度容量关系而考虑分时电价波动的风电站运行方案。

仿真运行结果如图12所示。

分析图12 可知，考虑温度容量关系的调度策略使得电池寿命损耗估计更加接近实际损耗，且能通过温度调节系统主动调控电池运行温度，便于针对不确定的分时电价灵活调整储能系统调度方案，可获得更高且更稳定的收益，验证了本文所提方案的优越性。进一步对比光伏电站与风电站，可知相对波动较小的光伏电站所配储能系统不需频繁抑制光伏电站波动，从而可有效利用分时电价产生的盈利空间。

图12 基于不同方案的电站日收益Fig.12 Revenue of plant based on different scheme

4.3 考虑混合储能单元价格变化的模型分析

随着化学电池技术发展以及原材料价格变化，LFP与ALC价格并非一成不变，分析价格变化对于模型结果的影响有助于新能源联合储能场站及时应对未来多变的储能市场。为此，以当前100 kW·h LFP与ALC 总价格作为变化后ALC 与LFP 总价格，分析LFP 与ALC 价格比值变化后光伏电厂的经济调度下两种电池的利用率，结果如图13所示。

经济调度下电池日运行损耗率与储能电池利用率正相关，结合图13 可知LFP 因其良好的高倍率充放电能力，即使LFP价格高昂时，仍然保持较高利用率，而ALC 价格过高时极易被LFP 代替。因此，LFP相对ALC具有不可替代地位。考虑到未来LFP 与ALC 价格进一步变化，若LFP 价格并非显著高于ALC，储能系统配备一定容量LFP 十分必要，而LFP 与ALC 价格相差不大时可以省去ALC的配备。

图13 储能单元价格变化与电池日运行损耗关系（注：1ppm=10-6）Fig.13 Energy storage unit price changes in relation to daily battery operating losses

4.4 线性化求解方法的用时及精度分析

为进一步分析采取分片McCormick 方案在3.1小节中方案二产生的效应，采用以下求解方法对比分析。

求解方法一：直接采用McCormick 策略的求解方法。

求解方法二：采用分片McCormick 策略的求解方法。

求解方法三：基于文献[12]所提动态规划模型的求解方法。

考虑到风、光出力的不确定性，将风、光出力的综合误差视为随机误差，以X～N(1,0.15)作为原来实际出力的系数，将场景1、2 分别进行数据扩增。针对扩展得到的2000种场景，开展测试验证，求解仿真结果如表2所示。

表2 不同求解方案性能对比Table 2 Performance comparison of different solution schemes

由于文献[12]所提方案具有较高求解精度，因此将该模型所求电站盈利作为最优解，不同求解方案所得电站盈利与其比较即得求解精度。由表2分析可得如下结论。①直接采用McCormick 方案用时最短，但是由于松弛过多，得出的最优解集对应的电站盈利值需要重新核算。而经过核算可以发现最优解对应的电站盈利值较低，调度方案经济性较低。②采用文献[12]所提动态规划求解方法经济性最高，但是用时过长，难以满足储能电站实时调度的需求。此外，将此方案用于更大规模的储能电站时将会需要更长求解时间。③采用分片McCormick方案用时较短，经济性也较高，能够实现电站日内实时调度，具有较高的实用价值。并且可以预见，继续增加分片数可以提高调度方案的精确性，提升电站运行的经济性。

5 结论

本文面向风/光储联合电站，建立了一种兼顾温度调节系统耗费与电池寿命损耗的经济调度优化策略。为实现储能电站日内实时调度，提高调度策略的经济性与求解速度，采用了分片的McCormick方法线性化模型中存在的大量双线性项。结论如下。

（1）计及储能系统热管理的调度策略可以实现储能电池在安全温度限度内稳定运行，保证储能电站应对各种极端天气时能够可靠地为新能源场站提供跟踪计划出力以及平抑波动等功能，同时也能为电网实现削峰填谷的服务。且为风/光新能源场站提供平抑波动服务并不会额外增大电池损耗，反而能够充分利用储能电池，增大新能源联合储能系统盈利。

（2）通过合理控制温度调节系统功率能在满足电池充放电所需适宜温度的同时降低温度调节系统费用。在储能电池充放电时提供更为适宜的电池温度以降低电池损耗成本，而在电池闲暇时刻节省温度调节系统费用，实现储能电站的经济、稳定运行。并且本文所提调度策略内电池寿命损耗估计更加接近实际损耗，且能通过温度调节系统主动调控电池运行温度，可以调整调度策略有效应对并网电价波动，最终实现电站日运行收益提高。

（3）LFP因其良好的高倍率充放电能力，即使LFP价格高昂时，仍然保持较高利用率，而ALC价格过高时极易被LFP代替。未来LFP价格并非显著高于ALC 时，储能系统配备一定容量LFP 十分必要，而LFP 与ALC 价格相差不大时可以省去ALC的配备。

（4）分片的McCormick 线性化方法既满足了电站实时调度的速度需求，也实现了高度经济的电站调度策略。并针对更大规模、更高时间精度要求的储能电站调度场景提出了增加分片数，以更严格的边界约束来保障调度方案经济性的策略。