结合高斯过程回归与特征选择的锂离子电池容量估计方法

韩云飞，谢 佳，蔡 涛，程时杰

（华中科技大学电气与电子工程学院，强电磁工程与新技术国家重点实验室，湖北武汉 430074）

锂离子电池以其高能量密度、高输出电压、低自放电率、低电压降、易于管理等优点被广泛应用于家用电器、智能手机、电动工具、储能系统、电动汽车等领域[1]。准确的锂离子电池容量和健康状态(state of health)估计对于确保系统的安全可靠运行至关重要。

目前针对锂离子电池的预测主要分为模型驱动(model-driven)方法和数据驱动(data-driven)方法[2]。模型驱动方法从实际的老化机制出发对电池进行建模， 例如固体电解质层(solid-electrolyte interphase，SEI)生长[3]、活性物质损失[4]等。然而锂离子电池的容量衰减与许多机制有关，如电极/电解液界面的副反应、活性物质的损失、电阻的增加以及与复合电极相关的问题，如集流体、孔隙率、黏合剂等的变化[5]，并且这些机制可能在电池内相互作用[6-7]。锂离子电池复杂的老化机制使得模型驱动的方法难以兼顾所有老化因素，因此受到了限制。

为了解决上述问题，数据驱动方法开始受到关注。数据驱动主要基于实时采集电池的运行数据，采用机器学习的模型将测量数据直接映射至目标值。这一方法不需要深刻掌握目标领域的背景知识。文献[8]使用循环神经网络实现电池的荷电状态(SOC)估计，文献[9]结合集成经验模态分解与门控循环神经网络对电池的剩余使用寿命进行预测。数据驱动方法的挑战在于选择合适的输入和模型。输入可分为原始数据和特征选择的数据。为了准确评估及预测电池的老化状态，模型的输入需要能充分反映电池的状态特征。文献[10]对电池使用容量增量分析(incremental capacity analysis，ICA)，建立了不同ICA 曲线与电池健康状态的映射。由于ICA 需要对电池进行特定倍率的充放电，且ICA 的微分操作对噪声十分敏感，因此不适合在线应用。文献[11]选择电池的阻抗谱(EIS)作为输入，建立高斯过程回归模型预测电池的容量和剩余寿命。虽然EIS 能较好地反映电池的老化状态，但EIS 测试缓慢复杂且需要特定的测试设备，难以在线应用。文献[12]选择原始的电压、电流、温度数据作为输入，采用深度学习分别进行电池的健康状态和剩余寿命的预测。虽然深层神经网络具有从原始数据中提取深层特征的能力，但同时也意味着多维的原始数据需要更大规模的网络去拟合。网络的规模越大，对训练数据的量和计算能力的要求也越高。

为了实现在线应用，需要从电池的在线可测量数据中进行特征选择。本文提出了一种结合高斯过程回归和特征选择的锂离子电池容量估计方法。具体而言，首先分析电池老化过程不同数据的演变模式，从电池的电压-放电容量曲线中进行特征选择，选择电池在片段电压上的累计放电容量作为特征，并将其作为高斯过程回归模型的输入，对电池的容量进行估计。

1 电池数据特征选择

数据驱动方法的成功与否不仅仅取决于算法本身，也取决于数据的表示方法，适当的特征选择能显著提升模型的性能。本部分结合领域知识介绍具有电化学意义的特征选择。

文献[13-14]提出了一种基于数据驱动的电池寿命预测方法。Severson等[14]对124个商用磷酸铁锂/石墨电池进行了全寿命周期的充放电测试。基于从电压-放电容量曲线中提取的特征建立弹性网络模型，由电池容量还未衰减的前100圈循环的数据即可预测出电池的循环寿命，误差为9.1%。图1展示了文献测试的放电容量随循环老化的变化曲线，可见不同电池的老化特性存在差异。图2展示了电池在不同循环的容量-电压(Q-V)曲线，可以发现随着循环老化电池的Q-V曲线遵循着一定的模式变化。

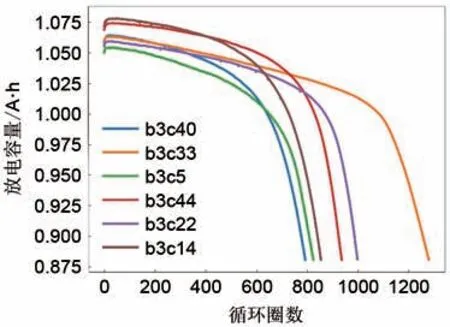
图1 不同电池的放电容量随循环变化Fig.1 Discharge capacity degraded with cycle number for different batteries

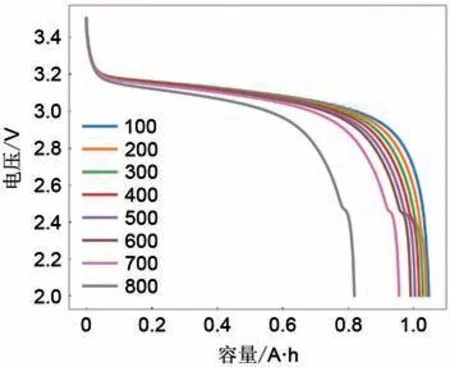
图2 电池不同循环的电压-容量曲线Fig.2 Evolution of voltage-capacity curves of battery with cyclic aging

从图1 和图2 可以看出，在早期循环中电池的退化模式并没有导致明显的容量衰减，但是在容量-电压曲线中有所表现。这可能是由于脱锂负极活性物质的损失导致Q-V曲线在容量不变的情况下发生变化。当负极相对正极过量时会出现这种现象，而这一种现象在商用锂离子电池中是比较普遍的。因此，脱锂负极的损失改变了锂离子储存的电位，而没有改变总容量[15]。从能量的角度来看，随着电池的老化Q-V曲线的变化表现为曲线下面积的变化，对于第N和M圈循环有

式中，∆EN−M表示第N和M圈释放能量的差值；∆QN−M表示在给定无穷小电压区间dV上第N和M圈循环累积容量的差值。这表明随着电池的老化，其可存储和释放的能量会减少。

该特征选择以电压作为自变量，因为电池的工作电压区间比较固定。而以电压为因变量时，该特征描述了电化学过电位的概念。过电位是电极的电位差值，为一个电极反应偏离平衡时的电极电位与该电极反应的平衡电位的差值。在等效电路中过电位为欧姆内阻和极化内阻的电压差之和。随着电池的老化，极化加剧，过电位发生变化，在容量-电压曲线上体现为曲线的偏移。由上述分析，电池的电压-容量曲线是进行电池状态预测及诊断的优秀数据源。如何从曲线中进行特征提取是建立高性能数据驱动模型的关键。

由于实际工况下电池通常不会进行完整的充放电循环，为了模拟实际的电池运行工况，选择电池的部分电压区间的容量数据作为选择的特征，如图3所示。具体而言，电池管理系统可以在线采集电池的电压、电流值。通过安时积分可获得电压和容量的曲线，采用样条函数插值后可以计算设定的电压点上的容量值，如图3 选择了3.2～2.75 V 的30个等间隔点，计算如式(2)所示。

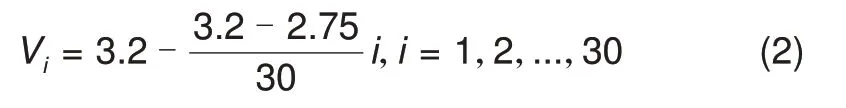
Vi点对应的特征记为Qi，则模型的输入为[Q1,Q2,…,Q30]。

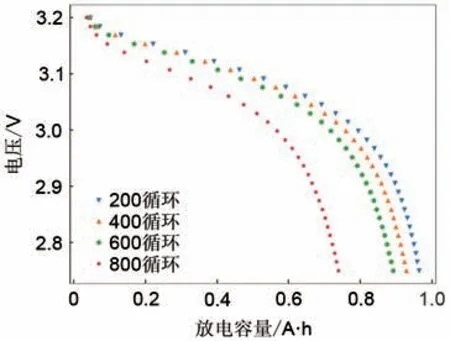
图3 模型的输入特征Fig.3 Input feature of the model

2 基于高斯过程回归的容量估计模型

本文提出的电池容量估计模型的流程如图4所示。首先从电池的电压-放电容量曲线上选择片段电压区间，并根据样条插值获得特征输入。模型的训练数据集表示为D={(xi,yi),i=1,2,…,n}，xi为特征输入，yi为电池的容量，n为样本数。根据训练数据离线训练GPR模型。对电池进行在线容量估计时，首先监测电池的运行电压范围是否覆盖了预先设定的电压区间。如果不满足要求，则继续对电池进行监测。如果满足要求，则从对应电压-容量曲线上提取特征，输入GPR模型中估计电池的容量值。

GPR作为一种贝叶斯方法可以产生具有概率上下界的置信区间[16]。这对于做出决策至关重要，因为在实际的诊断估计中不仅关注估计的值，也关心估计值的不确定性。同时GPR作为一种非参数方法(non-parametric)能根据训练数据的量调整模型的表达能力，而不像神经网络需要大量训练数据支撑。

定义函数f: ℝ→ℝ 为输入特征到电池容量的映射，输入特征与输出的关系表示为

其中εi～N(0,σ2)为独立同分布的高斯噪声，不同的样本服从多维联合高斯分布，无穷维的高斯分布构成高斯过程

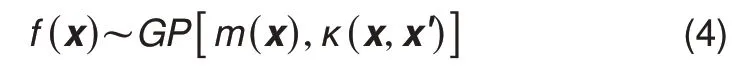
式中，m(x)为均值函数，κ(x,x')为方差核函数。假定输出服从联合高斯分布，给定训练数据，则训练数据和测试样本的联合分布也为高斯分布

由贝叶斯回归，可以求出y*的后验概率，均值函数为

协方差矩阵为

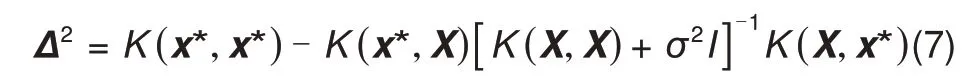
均值函数设置为0，核函数选择带有自动确定相关(automatic relevance determination，ARD)的径向基核函数(radial basis function，RBF kernel)

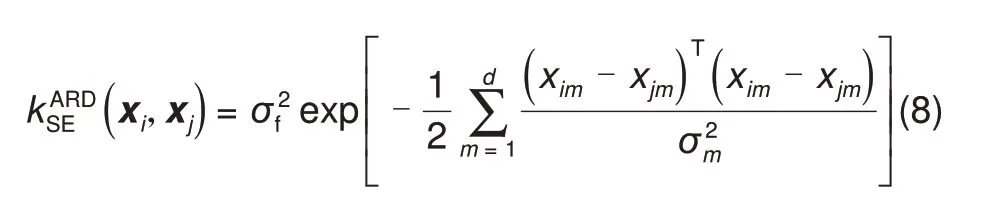
系数σm表示特征m的长度比例，σf表示特征的标准差。所有的超参数通过极大似然估计(MLE)进行优化。ARD类似正则化会让模型变得稀疏。

所有的输入数据采用训练数据的均值和方差进行了标准化，如式(9)所示，其中μ和σ分别为训练集输入特征的均值和方差

3 实验结果与分析

为了验证本文提出的特征选择结合数据驱动模型的预测性能，本节在两种不同的电池数据集上进行实验，并比较了该方法与采用阻抗谱作为输入的模型的性能。

3.1 锂离子电池测试数据集

本文使用的电池数据集包括Cambridge 数据集[11]和MIT-Stanford 数据集[14]。Cambridge 数据集包括了12 个钴酸锂/石墨电池的阻抗谱测试和容量测试数据。电池的充放电均为相同的恒流-恒压模式，其中8 个电池的测试温度为25 ℃，2 个为35 ℃，2 个为45 ℃。在电池进行完整的充放电循环过程中穿插阻抗测试。MIT-Stanford数据集包括了124个磷酸铁锂/石墨电池的循环测试数据。电池的额定容量为1.1 A·h，额定电压3.3 V。所有电池都被置于30 ℃的恒温箱内进行大倍率的充放电实验。电池采用备选的不同快速充电模式进行充电，并采用相同的放电模式。在测试过程中记录电池的电压、电流、温度等数据。当电池的容量衰减至额定容量的80%时终止测试。

3.2 Cambridge数据集

为了模拟实际的电池充放电状态，选择电池3.8～3.3 V的放电区间作为特征选择的区间。在区间内等间隔取50 个点，进行拟合后记录下对应电压点的容量值作为特征输入，即模型的输入为长度50的向量。由于Cambridge数据集只有6个电池的数据记录了电压，因此将6 个电池中的5 个选为训练集，剩下的1个为测试集。轮流选择电池数据作为测试集以验证模型的泛化能力。

图5为不同的电池作为测试集时的容量估计结果。其中实际容量值为红色三角形，估计容量值为绿色星形，橙色区间表示估计值的1倍标准差。决定系数显示在图的左下角。图6 为3 个电池的测量容量值与估计容量值的对比。虽然各个电池的循环寿命和容量衰减趋势各不相同，但模型的估计值基本可以追踪电池的实际容量变化。这一结果说明了选择的特征能有效反映电池的老化状态。选择均方根误差(RMSE)和平均百分误差(MAPE)评估模型的性能。

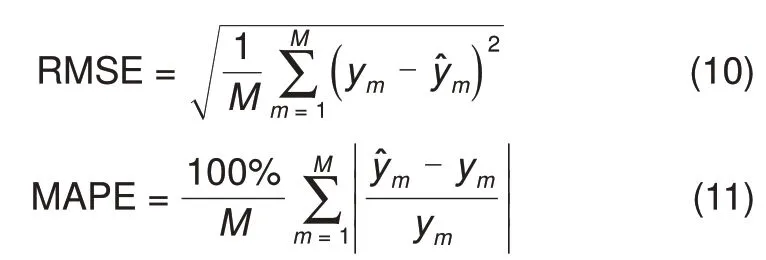
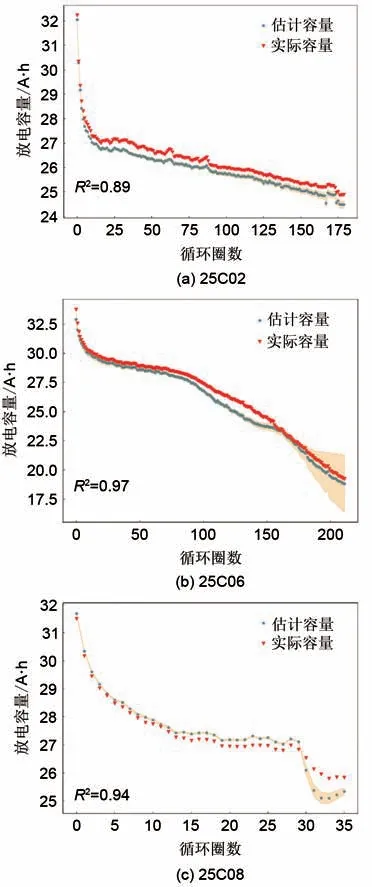
图5 Cambridge数据集的容量估计结果Fig.5 Capacity estimation result on Cambridge dataset

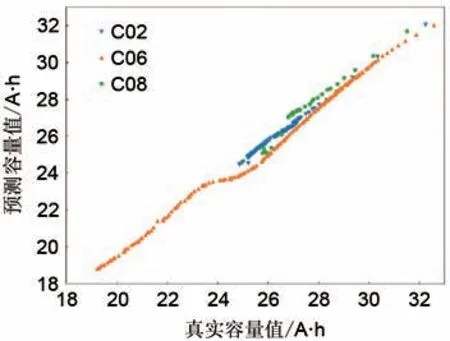
图6 测量容量与估计容量对比Fig.6 Measured capacity against estimated capacity

式中，ym为实际容量值；ŷm为模型的估计容量值；M为样本数。表1为以不同电池数据作为测试集时的模型性能。

表1 Cambridge数据集模型性能Table 1 Model performance on Cambridge dataset

为了验证该特征选择的性能，将文献[11]的方法与本文的方法进行对比。文献[11]采用阻抗谱作为模型输入，估计电池的容量。阻抗谱的输入包括60 种不同频率下测量的阻抗实部和虚部，即输入为长度120 的向量。同样建立GPR 模型，训练集和测试集的划分与上述实验相同，图7显示了其中一个测试集的容量估计结果。可以发现该估计结果存在较大的误差。

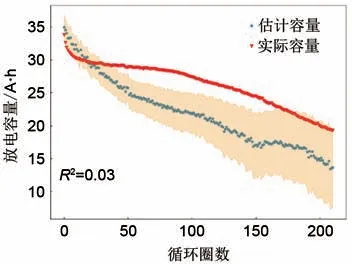
图7 阻抗谱作为输入的模型估计结果Fig.7 Capacity estimation result with EIS input

采用阻抗谱作为输入时的模型性能见表2。与表1 对比可见采用电压-容量曲线的特征估计容量能取得更好的性能。

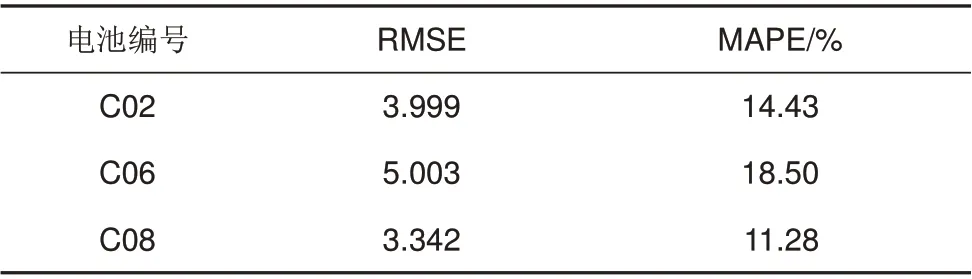
表2 阻抗谱作为输入时的模型性能Table 2 Model performance with EIS input

3.3 MIT-Stanford数据集

为了进一步验证该方法的泛化能力，在MITStanford 数据集上进行了实验。选择数据集中第3批次的电池c3～c7共5个电池的数据作为训练集训练GPR 模型。模型的输入特征选择电压区间2.75～2.3 V，等间隔选择30 个数据点，即输入向量长度为30。在剩下的电池中随机选择测试数据，容量估计结果如图8 所示。图8(a)和(b)分别为GPR 对两个电池的容量估计结果，可以发现该方法依然可以获得较好的估计结果。表3为模型在测试集上的性能评估结果。

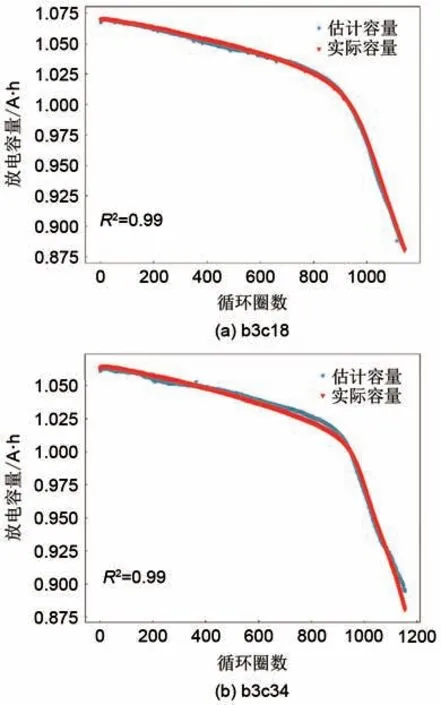
图8 MIT-Stanford数据集的容量估计结果Fig.8 Capacity estimation result on MIT-Stanford dataset

表3 MIT-Stanford数据集模型性能Table 3 Model performance on MIT-Stanford dataset

为了进一步研究不同电压区间对模型性能的影响，选择了3.5～3.275 V，3.2～2.975 V，2.75～2.525 V 区间内的特征作为输入，其中每个区间等分为15份，即输入为长度15的向量。不同电压区间的输入特征的模型性能见表4，可以发现在3.5～3.275 V 区间的模型估计误差明显大于其他两种模型。由图2 可知，随着电池的老化，3.5～3.275 V区间的Q-V曲线的变化并不明显，GPR模型难以通过该区间的电压-容量关系对电池的老化状态进行学习，因此导致该区间的数据作为输入时的模型性能下降。这一结果说明电压区间的选择对模型的性能有一定影响，如在线应用，需考虑计算和存储资源的限制，选择适当的电压区间进行特征提取。

表4 不同电压区间输入的模型性能Table 4 Model performance with different voltage interval input

4 结论

结合特征选择与高斯过程回归提出了一种数据驱动的锂离子电池容量估计模型。只需测量电池的片段电压和电流数据即可实现在线的容量估计，而不需要进行完整的充放电循环。从电池的电压-放电容量曲线上提取的特征作为模型输入，使用具备预测不确定性的GPR 作为回归模型预测电池的容量。在钴酸锂电池和磷酸铁锂电池数据集上的实验验证了该方法的有效性和泛化能力。与文献采用阻抗谱进行容量估计的方法相比，本文的模型性能较好。说明电池的电压-放电容量曲线是对电池进行状态评估及诊断的优秀数据源。采用不同电压区间提取特征的模型性能存在差异，表明不同的电压区间在反映电池的老化状态时所蕴含的信息量是不同的。未来的工作中我们会验证该方法在不同温度环境下的适用性，并优化特征提取的电压区间。