钠离子电池健康状态预测

冯一峰，沈佳妮，车海英,2，马紫峰,2，贺益君，谈 文，杨庆亨

（1上海交通大学化学化工学院，上海电化学能源器件工程技术中心，上海 200240；2浙江钠创新能源有限公司，浙江绍兴 312000；3上海派能能源科技股份有限公司，上海 201203）

近年来，随着储能、电动汽车和电子消费品的迅速发展，锂离子电池需求急剧增加，锂资源问题日渐凸显。相比于锂，钠盐储量丰富、提取工艺成熟，同时钠和锂作为同族元素具有类似的电化学特性，因此钠离子电池研究在近年逐渐成为新的热点，并在大规模低成本储能中展现出广阔的应用前景[1-6]。钠离子电池作为电化学存储器件，其工作过程中存在各类副反应。这些副反应的发生不仅会导致电池老化，还会引发安全事故。因此，针对钠离子电池特性，开发健康状态(state of charge，SOH)估计方法对于延长电池使用寿命，保证使用安全具有重要作用[7-8]。

SOH 是表征电池老化状态的指标，通常可定义为当前容量与初始容量之比。电池老化机理十分复杂，包括固体电解质界面膜溶解、电解液分解等多种电化学过程[9]，且受温度、电流和电压等多个因素影响。目前，钠离子电池老化研究仍处于初始阶段，机理尚未明确。考虑到钠离子具有较大半径，对电池相变行为和副反应影响更为显著，电池老化机理相较于锂离子电池可能更加复杂[10-11]，因此，准确构建钠离子电池机理模型非常困难。时间序列法是一种根据一定时间的数据序列对未来发展趋势进行预测的方法，计算速度快且能避免复杂的机理建模。针对锂离子电池，有研究提出从时间序列策略出发，通过建立可测参数与SOH 的复杂非线性关系，实现SOH 精准预测。考虑到钠离子电池工作机理与锂离子电池相似，本研究提出了钠离子电池SOH 时间序列预测方法，相关研究还未见公开报道。

常用SOH时间序列预测方法包括经验模型[12-14]和数据驱动模型[15-18]两种。经验模型利用指数、对数等函数模拟SOH 衰减趋势，简单直观。但由于电池特性在老化过程中持续变化，模型误差难以避免，需要结合状态估计算法进行模型参数更新。常用状态估计算法有粒子滤波类[19-20]和卡尔曼滤波类[21]算法，其中粒子滤波算法能够处理非线性、非高斯问题，适用于处理电池管理系统在线监测中存在的非高斯噪声，被广泛用于电池SOH 预测。Zhang等[12]建立了基于指数经验模型和粒子滤波的SOH 预测方法，实现了精准剩余使用寿命预测。Miao等[14]建立了基于双指数经验模型和无迹粒子滤波的SOH 预测方法。数据驱动模型从实验数据中训练获得SOH 时间序列的映射关系，包括人工神经网络[18,22]、支持向量机[16,23-24]和高斯过程回归[25-27]几类，其中高斯过程回归具有高效的非线性拟合能力和较高的预测精度，是常用的SOH 时间序列回归方法，Liu 等[17]建立了线性均值函数的高斯过程回归SOH 预测方法，实现高精度SOH 预测。此外，结合小波分析对SOH时间序列的多尺度解耦，高斯过程回归还能实现对SOH 全局退化趋势和局部波动的精准预测[28]。

为了系统比较经验模型和数据模型在钠离子电池SOH 预测中的有效性，本文选择双指数模型和高斯过程回归两种代表模型，分别建立了基于双指数模型的粒子滤波(DEM-PF)和基于小波分析的高斯过程回归(WA-GPR)方法，并在1 A·h 软包钠离子电池的1 C充放电老化测试下进行了验证。

1 健康状态预测方法

1.1 健康状态定义与问题描述

SOH 是评价电池老化状态的重要指标，基于容量的SOH定义为

式中，Cm为当前电池的最大可用容量；C0为新电池初始的最大可用容量。随着电池循环老化，SOH 呈衰减趋势。当SOH 退化到规定阈值时，可认为电池失效，本文选择电池的失效阈值为70%。从当前状态算起，到失效所剩余的循环圈数称为剩余使用寿命(RUL)。根据RUL可以对电池组的实际工况进行调整，在寿命终止前更换电池包，对延长电池使用寿命、保证安全具有重要意义。

基于给定SOH 时间序列D={(i, SOHi)|i=1,2,…,k}，i为循环圈数，SOHi为第i次循环对应的健康状态，可建立基于经验模型或数据驱动模型的映射关系f(·)∶i→SOHi，则从第k次循环算起，SOH预测问题可以表示为

式中，m为提前预测的步数。根据m取值的不同，SOH 预测问题主要分为两类：①单步SOH 预测：m=1，基于当前历史数据对下一次循环的SOH 进行预测，可为电池荷电状态的估计提供容量数据；②多步SOH 预测：通过单步预测递推实现多步预测，每次单步预测结果都被记入下步预测的历史数据。基于电池失效阈值，多步预测可以实现RUL预测。

1.2 DEM-PF方法

DEM-PF 方法利用双指数经验模型模拟SOH的衰减趋势，通过PF 算法对模型参数进行更新，以降低长期预测的误差累积，其计算流程见图1，主要步骤如下。

步骤1：离线模型构建。基于历史数据建立双指数模型，获取参数初值。

步骤2：在线参数更新。将模型参数作为PF算法状态变量，进行在线更新。离线模型的参数初值用于滤波粒子初始化。更新过程包括重要性采样、归一化权重计算、重采样和状态估计。

步骤3：健康状态预测。利用更新所得参数可进行单步SOH 预测，将单步预测值作为下步测量值，递推可实现长期RUL预测。

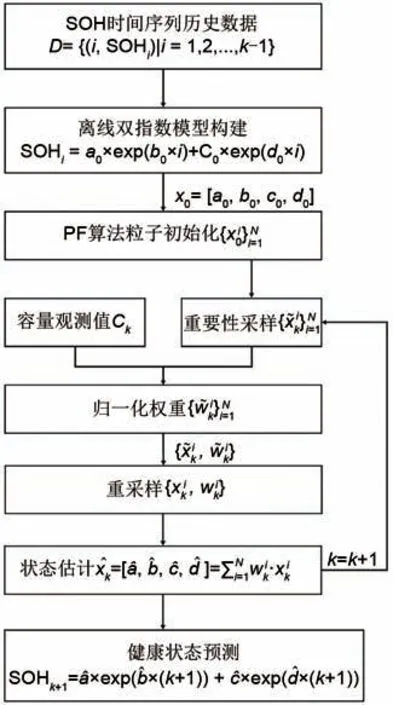
图1 基于双指数模型粒子滤波方法流程图Fig.1 Schematic of double-exponential model-based Particle filter method

DEM-PF方法中双指数经验模型表达式如下[29]

式中，k为循环次数，x=[a,b,c,d] 为模型参数，其初值x0=[a0,b0,c0,d0] 可以通过最小二乘法求解，结果列于表1。

表1 双指数模型参数初值Table 1 The initial parameter values of the double-exponential model

将模型参数作为PF状态变量，并利用表1中参数初值对PF粒子进行初始化，其状态转移方程为

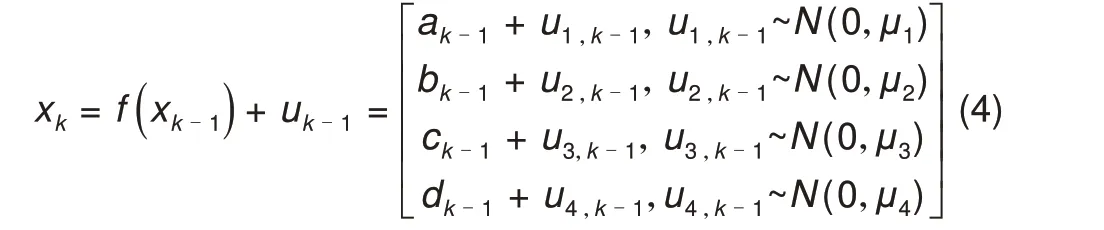
观测方程表示为

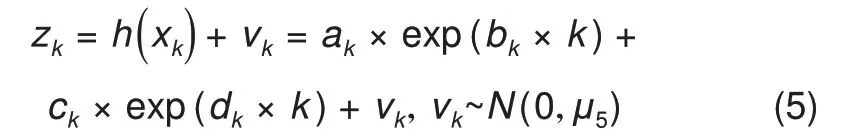
式(4)和(5)中，f(·)和h(·)分别为系统状态转移函数和观测函数。xk=[ak,bk,ck,dk]、zk、uk-1和vk分别表示状态变量、观测变量、过程噪声和观测噪声，uk-1和vk满足均值为0，方差为μ的高斯分布，其中方差根据对应变量绝对值的数量级选取，本文取变量绝对值的1.5倍。

根据贝叶斯理论，状态估计问题可以根据已有的后验知识z1∶k递推出当前状态xk的可信度p(xk|z1∶k)。PF基于贝叶斯理论，利用蒙特卡洛从后验概率中获取N个样本(粒子)解决后验概率计算积分难的问题，同时引入重要性采样方法进行后验概率未知情况下的采样，其中粒子数量会影响状态估计精度，粒子数量过多会导致计算量过大，本文选择粒子数量为1000。设重采样概率密度函数为q(x0∶k|z1∶k)，后验概率密度p(xk|z1∶k)可以根据各粒子权重计算[30]

以上采样过程存在粒子退化过程，即权重主要集中在少数粒子上，有效粒子数变少，算法的状态估计性能下降。因此，引入重采样替换权重小的粒子，一般复制权重大的粒子进行取代，其比例可根据粒子权重的占比进行分配。重采样后，各粒子权重均等，后验概率密度函数表示为

1.3 WA-GPR方法

WA-GPR方法先利用小波分析获取电池老化的主趋势信号与细节信号，然后利用GPR 分别建立各信号的回归模型，将各信号的预测值进行组合，实现SOH 预测，其计算流程如图2 所示，主要步骤如下。

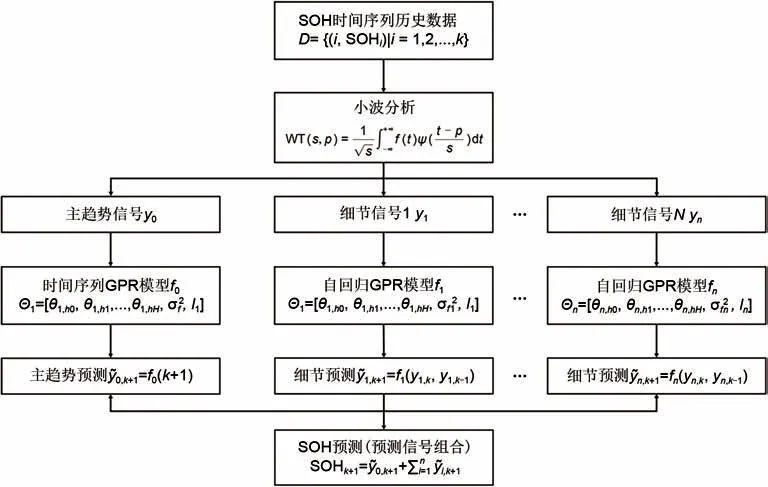
图2 基于小波分析的高斯过程回归方法流程图Fig.2 Schematic of wavelet-analysis-based Gaussian process regression method

步骤1：小波分析。利用小波分析将SOH时间序列解耦为主趋势信号与细节信号，细节信号的数量N表示小波分析的分解层数。

步骤2：GPR模型建立。①对主趋势信号建立时间序列输入的GPR 模型，使用线性均值函数和平方指数协方差函数；②对各个细节信号建立滞回向量输入的自回归GPR 模型，使用常数均值函数和平方指数协方差函数。

步骤3：各信号预测。利用所建立的GPR模型分别对主趋势和细节信号进行预测。

步骤4：健康状态预测，将预测值组合，获得单步SOH预测结果，递推实现RUL预测。

WA-GPR方法采用的小波分析是分析时序波动信号的有力工具[31]。电池SOH 的变化趋势可视为具有下降主趋势的波动信号，局部的再生与波动信号关联电池内部复杂的电化学过程，因此可以通过小波分析对SOH 信号进行多尺度解耦，以更准确地获取电池老化的趋势，提高SOH 预测精度。小波分析通过对母小波的位置平移和宽度缩放操作，获取信号的时间和频率特性，把原始信号分解为一系列小波。将信号序列f(t)在小波基函数下展开

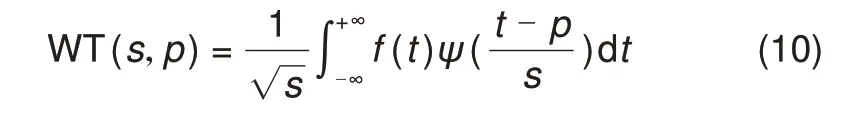
式中，Ψ(·)表示母小波函数；s为尺度参数；p为位移参数，分别控制小波函数伸缩和平移。上述小波分析中，s与p都是连续变化的，导致计算量巨大。为解决计算量问题，引入离散小波分析，采用离散的尺度和位移参数，常选用2j(j为正整数)的倍数。

GPR 为一种基于贝叶斯理论，使用高斯过程对数据进行回归分析的非参数模型[32]。对于给定训练集(X,y)={xi,，利用GPR可以建立训练集输入X与输出y之间的映射关系f=[f(x1),f(x2),…,f(xn)]

式中，m(X)为均值函数；K为协方差矩阵。在本文中使用线性均值函数来描述SOH 衰减的主趋势信号，可以表示为

WA-GPR 方法的函数和参数选择十分重要。在小波分析中，母小波函数选择多贝西四阶小波，分解层数选择5。在GPR 模型的超参数初值中，主趋势GPR 模型线性均值函数的斜率和截距分别设为0.5 和1，平方指数协方差的特征尺度和协方差均设为1。细节信号GPR 模型常数均值函数的初值以及平方指数协方差的特征尺度和协方差均设为1。

2 实验结果与讨论

实验测试对象为1 A·h 钠离子三元软包电池，其正极为NaNi1/3Fe1/3Mn1/3O2层状三元氧化物材料，负极为硬碳，电解液溶剂为碳酸乙烯碳酸酯与碳酸二乙酯，电解质为NaPF6，该电池体系可以表示为(+)NaNi1/3Fe1/3Mn1/3O2|NaPF6-EC/DEC|HC(-)。该电池的充电截止电压为3.8 V，放电截止电压为1.5 V。电池老化测试在25 ℃自然对流条件下进行，以1 C充放电循环测试至电池容量衰减到失效阈值70%。测试结果如图3所示，电池的使用寿命为635次循环，SOH 随着循环圈数增加呈现退化趋势，但仍伴随着局部波动，存在无规律的容量恢复和瞬降情况[33-34]。这些现象与钠离子电池内部复杂老化过程相关，涉及到固体电解质界面膜溶解、电解质分解、活性材料相变等多个过程。在电池老化过程中，SOH 的波动使模型的误差不断积累，模型难以预测真实的老化趋势。因此，DEM-PF方法利用PF 修正模型参数，WA-GPR 方法利用小波分析对时间序列SOH 进行多尺度解耦，都有助于提高SOH预测精度。

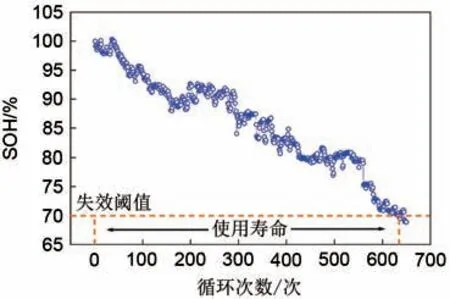
图3 钠离子电池SOH退化曲线Fig.3 The degradation curve of the sodium-ion battery

小波分析的结果如图4 所示，图4(a)表示近似的主趋势信号，图4(b)～(f)分别表示解耦所得不同尺度的细节信号。与原始SOH 时间序列相比，在去除高频和低频的波动后，提取的主趋势信号能够准确地跟踪电池的退化趋势，该信号可以在长期预测中帮助捕捉准确的SOH 退化趋势。但在第200 和500 次循环附近，该钠离子电池存在较为显著的容量再生或下降现象，对应区域的主趋势信号与原始SOH 的偏差相对较大。从细节信号图4(b)～(f)可见，细节信号1 和2 主要由高频的小振幅信号组成，这可能与电池内部复杂的电化学过程相关，受到电流、温度等因素的影响产生波动。容量的局部再生主要在较低频的信号3、4 和5 中出现，图中使用方框标出。需要指出的是，容量的再生或波动是共存的，与复杂的电化学过程相关，并不能够利用小波分析严格划分，但根据解耦获得细节信号能在一定程度上获取钠离子电池不同尺度的老化特性。

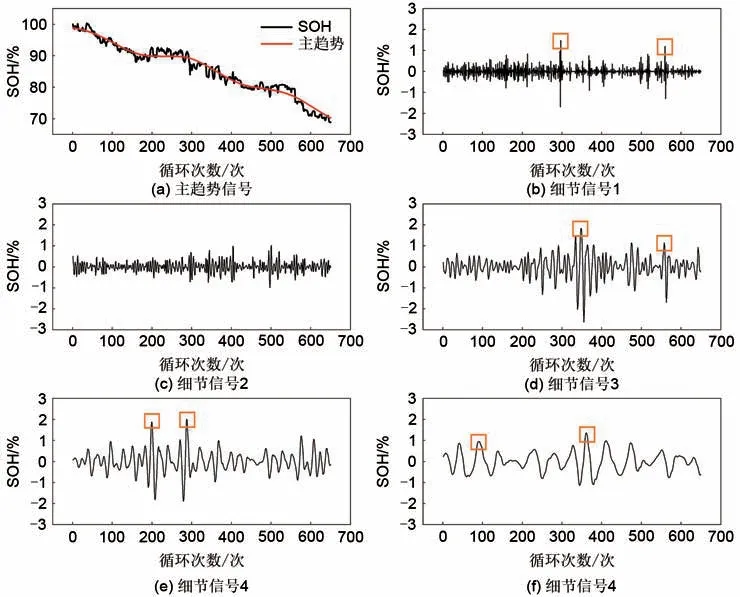
图4 钠离子电池SOH时间序列小波分析结果Fig.4 Wavelet analysis of SOH time series of the sodium-ion battery

单步SOH 预测结果如图5 所示。DEM-PF 方法和WA-GPR 方法的预测均方根误差(RMSE)分别为1.5%和0.8%。由图5(a)、(b)可知，DEMPF 方法虽能够获取SOH 的变化趋势，但由于双指数经验模型形式简单，即使通过PF 算法对模型参数进行更新，局部波动仍较大，对容量再生和波动不能准确描述，绝对值误差较大。相比之下，WA-GPR 方法通过对SOH 时间序列多尺度解耦，不仅能准确预测电池的退化趋势，还能通过细节信号的自回归基本还原局部的容量再生和波动，绝对值误差显著降低，实现精准的单步SOH 预测。

在RUL 预测中，分别设置预测起点为第100、200 和300 次循环，以探究不同历史数据对两种方法预测精度的影响，误差汇总于表2，结果汇总于图6，图6(a)、(c)和(e)分别表示起点为100、200和300 次循环的SOH 长期预测结果，图6(b)、(d)和(f)分别为对应的RUL预测结果图。由图可知，在多步SOH 预测过程中，DEM-PF 方法虽能一定程度反映电池的老化趋势，但是由于双指数模型形式简单，预测结果几乎为一条直线，无法对局部的容量再生和波动进行预测。WA-GPR方法通过解耦不同尺度信号，不仅能够准确预测电池老化主3.2%和2.5%，RUL预测误差分别为35、18和3次循环。相比之下，WA-GPR方法性能更优，能够实现更准确的RUL预测。

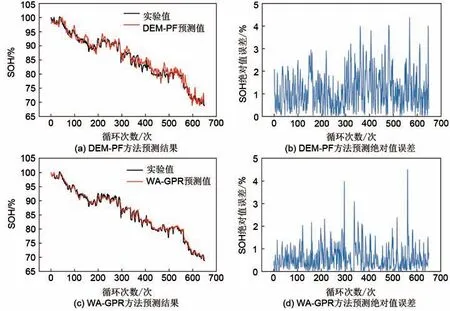
图5 钠离子电池单步SOH预测结果Fig.5 One-step-ahead SOH prediction for the sodium-ion battery

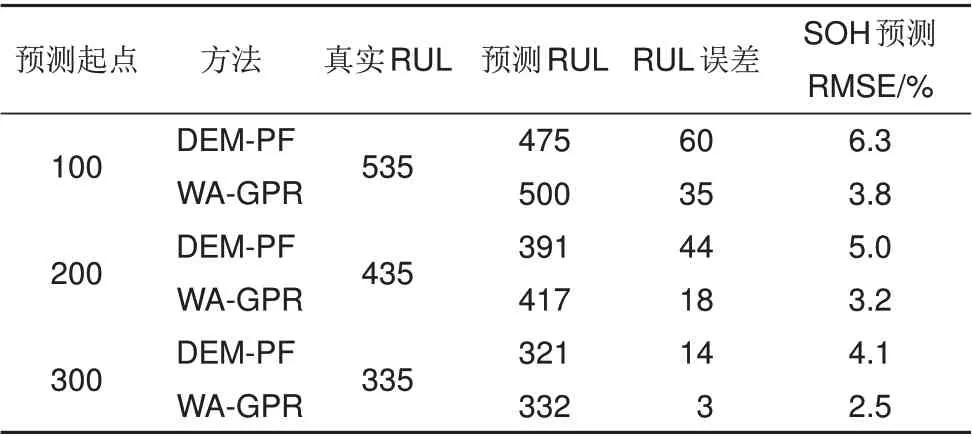
表2 不同预测起点下RUL预测误差Table 2 RUL prediction error with different starting points

3 结论

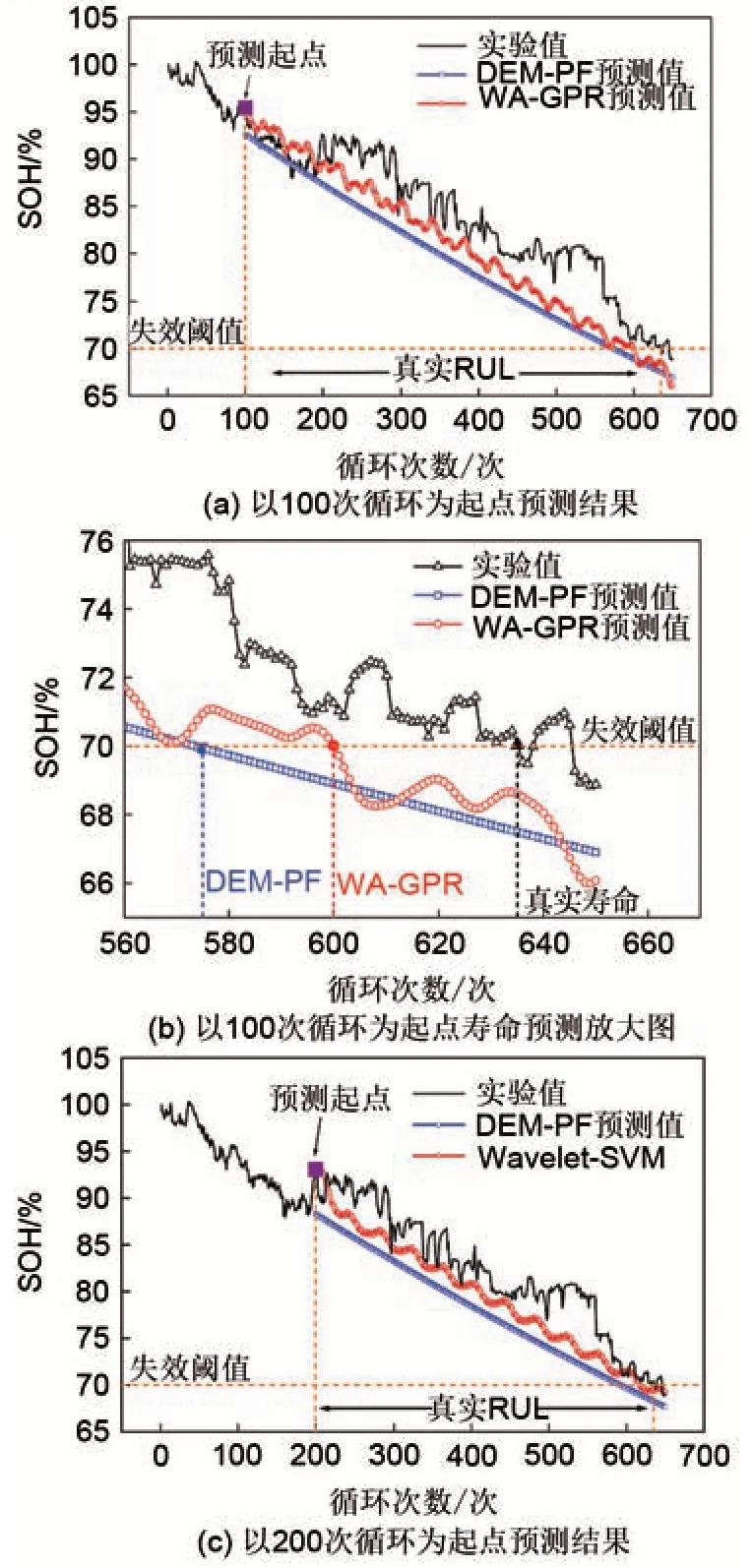
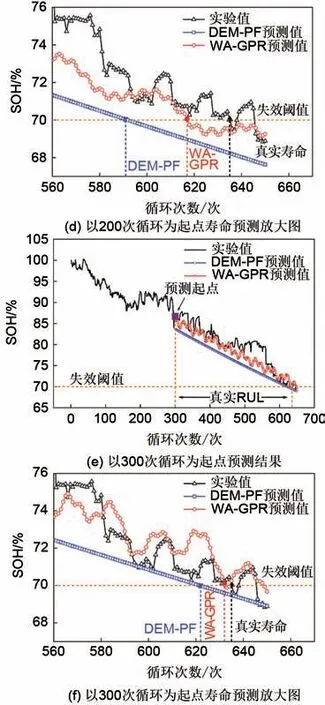
图6 钠离子电池RUL预测结果Fig.6 RUL prediction of the sodium-ion battery

本文针对钠离子电池，首次提出了两类基于时间序列策略的SOH 预测方法，即DEM-PF 法和WA-GPR法，并利用1 A·h 软包三元钠离子电池老化测试数据对两者性能进行了验证和比较。结果表明，DEM-PF 法单步SOH 预测RMSE 为1.5%，RUL 预测误差最小为14 次循环，WA-GPR 法单步SOH 预测RMSE 为0.8%，RUL 预测误差最小为3 次循环。在进行钠离子电池SOH 预测时，DEMPF 法由于采用双指数模型，形式较为简单，即使采用PF 算法进行参数更新，误差仍相对较大。相比之下，WA-GPR 法通过对SOH 时间序列多尺度阶耦和回归，可实现对全局衰减趋势和局部容量再生与波动精准预测，从而为钠离子电池全生命周期管理提供支撑。