基于Cuk电路的多交错对称式均衡方案
李 斌,许 磊,郑 征,胡丹丹,张国澎
(1河南理工大学电气工程与自动化学院,河南焦作 454000;2国网河南省电力公司焦作供电公司,河南焦作 454100)
为应对能源危机和环境污染,《新能源汽车产业发展规划(2021—2035 年)》指出到2035 年电动汽车将成为销售车辆的主流[1]。锂电池以能量密度高、循环寿命长和无记忆性等优势,受到电动汽车的青睐[2]。为满足电动汽车动力需要,锂电池常以电池组的形式出现,但由于制作工艺与使用环境的不同,导致电池组能量存在不一致性,影响电池组的使用寿命和能量利用率[3]。因此,电池均衡方案已成为新能源汽车领域研究的热点。
目前,国内外研究的电池均衡电路为能量非耗散型均衡,主要为电容式均衡[4]、LC均衡[5-7]、变压器均衡[8-10]和电感式均衡[11-16],其主要是通过储能元件实现能量的转移。而电感式均衡因均衡电流可控,体积小、控制方式简单成为国内外主要研究的方向。
电感式均衡拓扑结构以非隔离型DC/DC 变换器为主。传统的电感式均衡通过变换器实现能量在相邻电池间的转移,但是存在均衡路径长、均衡速度慢的问题。文献[13]针对这个问题,与开关矩阵结合实现了任意电池间的能量传递,但是由于仅有一个均衡模块,均衡速度慢;文献[14]采用Cuk 电路与开关矩阵结合的方式,延长电池的能量转移时间,但同样存在每次仅能在一对电池均衡的问题;文献[15]采用分层思想搭建了两级双向Buck-Boost均衡电路,缩短了均衡路径,提高了均衡速度,但同一级下仍然存在仅相邻电池间能量转移的问题。文献[16]搭建了多输入多输出的均衡电路,实现能量动态转移,但能量转移过程仅发生在开关管导通期间。因此,快速的均衡拓扑仍然是研究电感式均衡的主要方向之一。
本文结合Cuk电路和分层均衡思想[17],提出一种基于Cuk电路的多交错对称式均衡方案。该方案以串联电池组中的单体电池作为研究对象,建立单体电池均衡电流与均衡模块控制信号占空比的数学关系,根据单体电池荷电状态(state of charge,SOC)偏差,并通过引入中止参数进行均衡策略设计与优化,完成各均衡模块的占空比计算,最终实现电池组的均衡控制。该方案结构简单、易于扩展,同时缩短了能量转移路径,在均衡速度上有明显优势。最后通过仿真平台完成了对上述控制方案的验证。
1 均衡拓扑结构和工作原理
1.1 均衡拓扑结构
本文提出的均衡拓扑结构如图1所示。
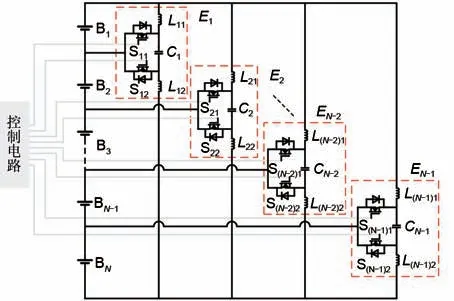
图1 均衡结构原理图Fig.1 Schematic diagram of the equilibrium structure
该均衡拓扑由电池组和均衡模块组成。电池组由N节电池串联构成,分别表示为B1、B2、……、BN;此外,拓扑具有N-1个均衡模块,分别表示为E1、E2、……EN-1。对于任意一个均衡模块En,它由储能电感Ln1和Ln2、电容Cn、开关管Sn1和Sn2构成,并形成双向Cuk斩波电路;通过控制均衡模块En中开关管Sn1和Sn2的通断,可实现前n个电池与剩余N-n个电池的均衡。
1.2 工作原理
均衡拓扑结构中第n个均衡模块En,如图2所示。
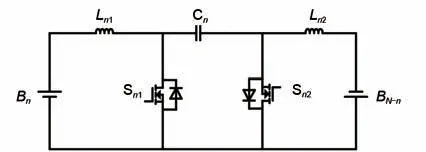
图2 均衡模块结构图Fig.2 Equalizing module structure diagram
在分析均衡模块的工作原理时,假定均衡模块中开关管Sn1和Sn2均具有理想特性。为了避免出现电感磁滞饱和的现象,均衡模块将工作在电流断续模式(DCM)。在DCM 模式下,设电池组Bn能量高于电池组BN-n的能量,此时均衡过程可分为三个阶段,其工作时序波形如图3所示。图中iLn1、iLn2为流过电感Ln1、Ln2的电流;uC为电容Cn两端电压;D1为开关管Sn1的控制信号占空比;D2为开关管Sn2的体二极管续流时的占空比。

图3 均衡模块工作时序波形图Fig.3 Equalization module working time sequence waveform
第一阶段(0~D1T):开关管Sn1闭合,Sn2断开,如图4 所示。电池组Bn通过电感Ln1放电,电感Ln1进行能量存储,电流iLn1增大。同时电容Cn释放能量,对电池组BN-n充电和电感Ln2储能,电流iLn2增大。该阶段电感Ln1、Ln2的电压和电流如式(1)所示。
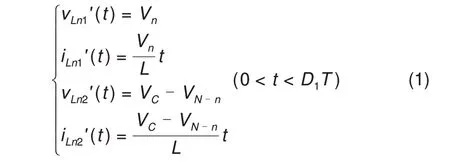
式中,Vn为电池组Bn的电压值;VN-n为电池组BN-n的电压值;VC为电容Cn的电压值。
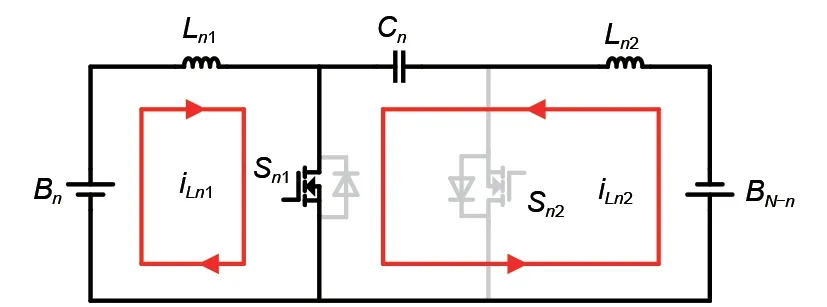
图4 第一阶段工作原理图Fig.4 Schematic diagram of the first stage
第二阶段[D1T~(D1+D2)T]:当t=D1T时,iLn1和iLn2均达到最大值,此时Sn1断开,Sn2的体二极管导通续流,如图5 所示。电池组Bn和电感Ln1释放能量给电容Cn,电流iLn1减小。同时,储存在电感Ln2的能量进行释放,电池组BN-n充电,电流iLn1减小。该阶段电感Ln1、Ln2的电压和电流如式(2)所示。
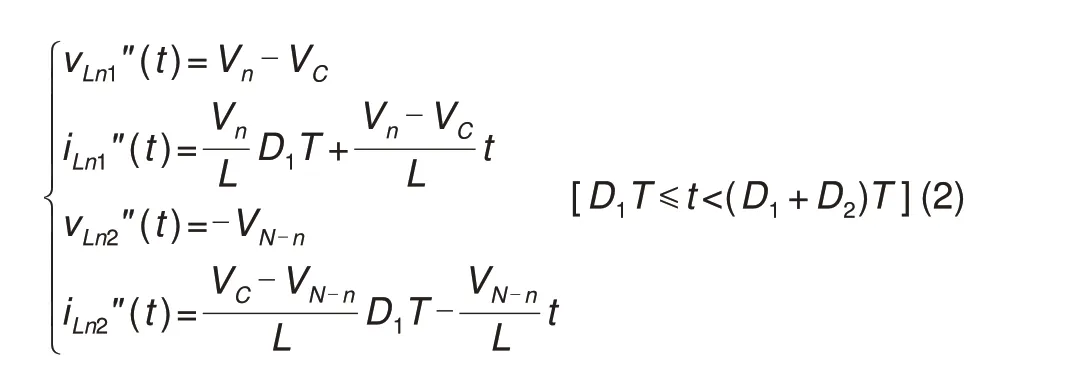
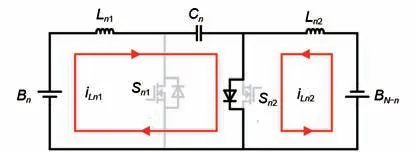
图5 第二阶段工作原理图Fig.5 Schematic diagram of the second stage
第三阶段[(D1+D2)T~T]:当t=(D1+D2)T时,iLn1和iLn2均减小到零,开关管Sn1和Sn2均闭合,电池间无能量转移,如图6所示。
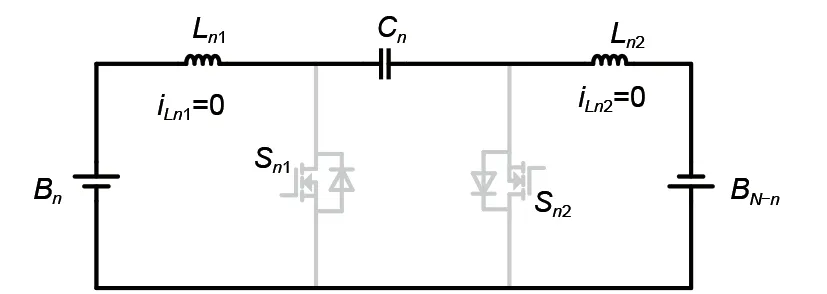
图6 第三阶段工作原理图Fig.6 Schematic diagram of the third stage
根据式(1)和式(2)可知,经过电池组Bn的平均均衡电流IEn为

依据电感伏秒平衡特性,可得
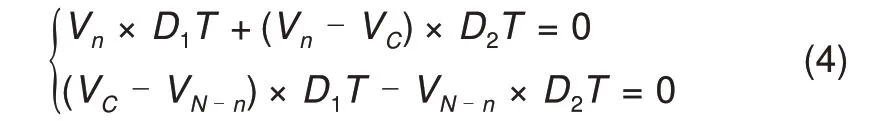
忽略均衡模块自身损耗,均衡模块两端电池组功率相同,即Vn×In=VN-n×IN-n,并结合式(4)可得

综上所述,均衡模块实现整个串联电池组的能量转移,并通过多个均衡模块分层工作,增大了均衡电流,提供了能量流动的多路径和克服了能量仅在相邻电池间传递的缺点。双向Cuk斩波电路通过储能电容的作用,延长了周期内能量转移的时间,避免了高能量电池仅在开关管导通期间进行能量转移的现象。
2 均衡控制策略
作为电池能量判别依据,SOC 是目前均衡变量的主流选择[18]。均衡电路工作时,流入电池的平均电流Ib可由式(6)表示

式中,Ic为平均充放电电流;Ie为平均均衡电流。

式中,SOCi为第i个电池的SOC;SOC0为SOC初始值;η为库仑效率,设置为1;Qn为电池额定容量;ΔSOCi为第i个电池的SOC与平均值的偏差。
为了实现电池组能量均衡,确保各单体电池的SOC 达到总电池的平均值。只需对电池Bi的均衡电流Iei进行控制,并使其满足式(10)
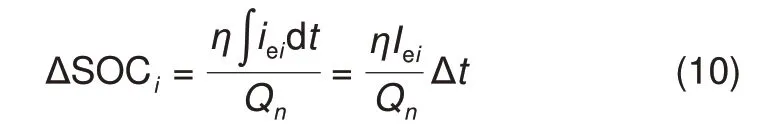
电池Bi的均衡电流Iei是各均衡模块共同作用的结果。为了便于分析各电池的均衡电流,本文假设电池的端电压相同并且设为VB。针对电池组中各电池的分布情况进行如下分析
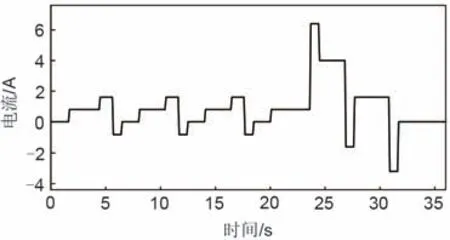
(1)电池Bi(1 a均衡模块En位于电池Bi上侧(n 均衡模块En工作时,通过图2分析可知,电池Bi处于图2 的电池组BN-n中。当开关管Sn1工作时,电池Bi处于均衡充电状态,经过电池Bi的平均均衡电流可由式(11)表示;当开关管Sn2工作时,电池Bi处于均衡放电状态,经过电池Bi的平均均衡电流可由式(12)表示 式中,Dn1为开关管Sn1控制信号占空比;Dn2为开关管Sn2控制信号占空比。 b均衡模块En位于电池Bi下侧(i≤n≤N-1)。 均衡模块En工作时,通过图2 分析可知,电池Bi位于图2 的电池组Bn中。当开关管Sn1工作时,电池Bi处于均衡放电状态,其平均均衡电流可由式(13)表示;当开关管Sn2工作时,电池Bi处于均衡充电状态,其平均均衡电流可由式(14)表示 (2)电池Bi位于串联电池组首端或者末端。此时,均衡模块仅分布在该电池一侧,故只需对一侧的均衡模块进行分析,如上述分析相同,此处不再重复分析。 综上所述,电池Bi的均衡电流Iei可用均衡模块的占空比表示,具体如式(15)所示 考虑到当相邻电池的SOC 相近时,两电池间的均衡模块仍持续工作,增加电路损耗。因此,本文针对各均衡模块,提出中止参数σ和中止阙值θ。如式(16)所示,当相邻电池的SOC 差值大于θ时,设置参数σ为1,均衡模块正常工作;而当相邻电池的SOC差值小于等于θ时,设置参数σ为0,均衡模块停止工作。同时,可取相邻电池的SOC 平均值代替原来相近的电池SOC值。 结合式(10)、(15)和式(16),并写出矩阵形式,可得电池SOC的偏差式(17) 为了确保均衡电路工作在DCM 模式下,必须满足D2<1-D1。根据式(5)可得,均衡模块En的控制信号占空比Dn1和Dn2可表示为 根据式(17)和式(18),在已知电池组各电池SOC 的条件下,可得到各均衡模块控制信号占空比,实现电池组的均衡控制。 本文以10节电池串联的电池组作为研究对象,基于MATLAB/Simulink 仿真环境搭建均衡系统仿真模型。为了缩短仿真时间并验证均衡电路效果,本文将电池容量设置为1 A·h,同时设置静置工况和动态工况进行仿真验证。仿真模型的其他参数设置如表1所示。 表1 均衡电路的参数表Table 1 Parameters of balancing circuit 为了对比验证,在静置工况下,除了搭建了本文研究的均衡方案外,另外搭建了文献[15]中的两级Buck-Boost均衡方案和文献[16]中的双向多输入多输出均衡方案。电池组中各电池的初始SOC设置及均衡后的变化情况见表2,静置工况下三种均衡方案的电池SOC 的仿真结果如图7 所示。由表2 可知,串联电池组在相同的电池SOC情况下,三种均衡方案都可以改善电池组的不一致性,使电池组的SOC极差从2.5%减小到0.5%。由图7可以看出,在均衡时间方面,文献[15]的均衡方案和文献[16]的均衡方案分别在213 s和41 s附近完成电池组均衡,而本文的均衡时间为18 s。相比较而言,本文所提的均衡方案在均衡时间上分别缩短了91.54%和56.1%。 表2 静置工况下不同均衡方案均衡前后电池SOC值Table 2 SOC values of batteries before and after different equalization schemes in static conditions 通过表2 和图7 的仿真结果可知,串联电池组中能量最高和最低的电池分别分布在电池组两端。对于文献[15]的均衡拓扑,虽然两级均衡结构可以一定程度上加快均衡速度,但当第二级模块的均衡过程结束后,第一级的均衡模块只能实现相邻电池间的能量转移,均衡路径长,均衡时间较慢;而对于文献[16]的均衡拓扑,多级均衡模块相互配合,均衡时间明显缩短,但能量传递仅发生在开关管导通期间,限制了均衡速度。而本文引入Cuk电路构成多级交错均衡系统,不仅能量传递路径灵活,而且均衡时间可以大幅缩短。 动应力测试(dynamic stress test,DST)工况作为一种典型的动态工况,其包含有放电、充电和静置三种工作状态。通过对该工况进行一定比例的设置验证均衡方案的有效性,如图8所示为DST工况的电流波形曲线图。 图8 DST工况下电流波形图Fig.8 Current waveform under DST condition DST 动态工况下,随机选取一组电池SOC 初始值进行本文均衡方案的仿真实验,其电池SOC均衡结果如图9所示。从图中可以看出,在该工况下电池组的能量持续减少,并在55 s附近均衡仿真结束,电池组的最大极差值从4%减少至0.5%,电池组的不一致性得到了极大地改善。通过仿真结果可以得出,本文提出的均衡方案在充电、放电和静置三种混合状态作用下可以保持较高的一致性,且均衡速度快。 图9 DST工况下串联电池组SOC仿真结果Fig.9 SOC simulation results of series battery pack under DST condition 综上所述,本文提出的均衡方案改善了文献[15]中能量在相邻电池间转移和文献[16]中能量仅在开关导通期间转移的缺点。通过静置工况和动态工况下的仿真,证明了均衡方案的可行性和有效性。此外,通过对比仿真验证,证明了本文均衡方案在均衡速度方面有明显优势,均衡时间可以大幅缩短。 针对串联电池组中电池间能量不一致问题,本文提出了一种基于Cuk电路的交错均衡方案,理论分析和仿真结果表明: (1)该均衡拓扑结构结合了Cuk电路和分层均衡优势,缩短了均衡路径,同时保证每个均衡模块都参与电池组的能量转移,增大了均衡电流,并延长了周期内能量转移的时间,加快了均衡速度。 (2)针对电池组中单体电池进行均衡策略设计,建立了均衡电流与控制信号占空比的数学关系,并引入中止参数进行优化。该均衡策略可以自适应调节均衡模块占空比,加快均衡速度,并改善了均衡效果。 (3)在不同工况下的仿真结果证明了本文均衡方案的有效性。此外,通过与不同均衡方案的对比验证,证明本文所提的均衡方案在均衡时间分别缩短了91.54%和56.1%,均衡速度更快,均衡效果更好。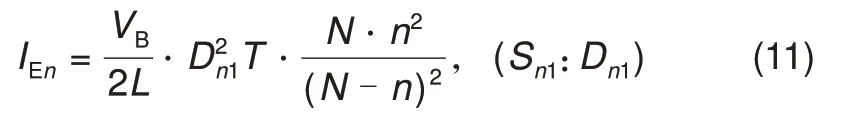
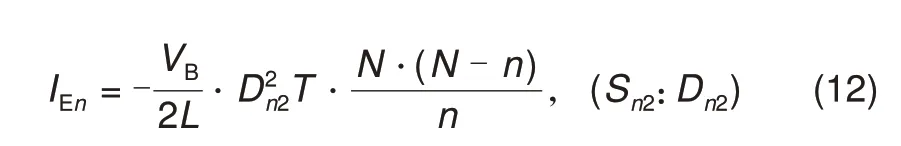
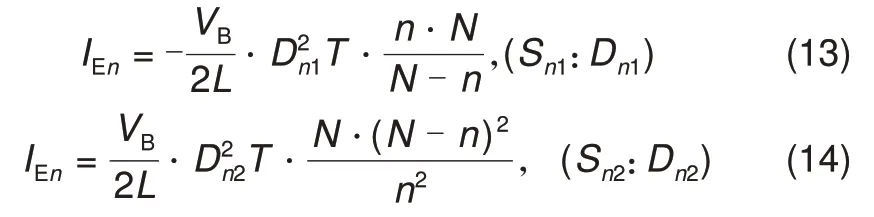
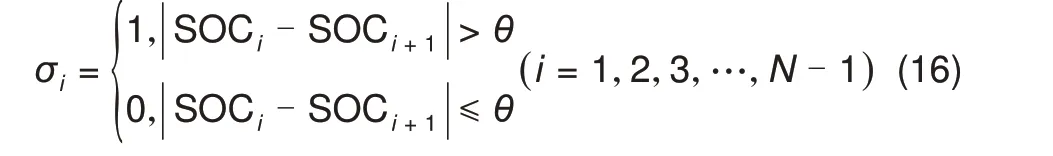
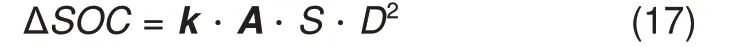
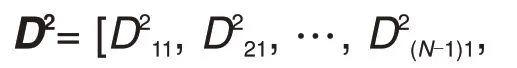
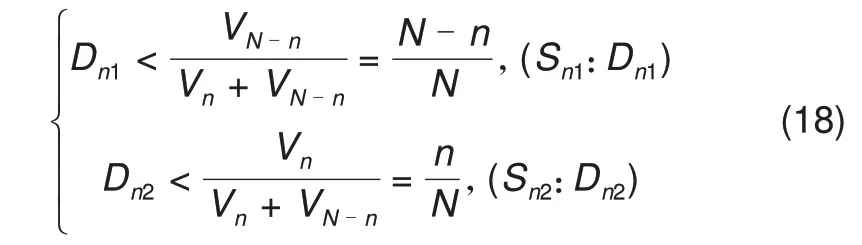
3 均衡仿真验证

3.1 静置工况仿真

3.2 动态工况仿真

4 结论

