全球供应链中残次品返工与多期延迟付款和部分延迟订购整合的协同效应

Wqs Ahmed , Muhmmd Mozzm , Biswjit Srkr *, Sif Ur Rehmn

a Department of Operations and Supply Chain, NUST Business School, National University of Sciences and Technology, Islamabad 44000, Pakista

b Department of Industrial Engineering, Yonsei University, Seoul 03722, Republic of Korea

c Department of Management Science, Lahore Garrison University, Lahore 54660, Pakistan

1. 引言

在一条全球性的供应链中，控制从供应商到最终客户的物料流是一个严峻的挑战。与从本地市场采购的公司相比，从全球市场采购的公司面临着更大的不确定性。采购提前期越长，其可靠性越低，并且会以管道存货的形式占用更多资金。瓶颈是显而易见的，也是每个供应链的固有部分。与库存管理相关的瓶颈之一是从供应商那里收到残次品。根据供应链委员会（Supply Chain Council）的说法，完美订单指的是在正确的日期和时间内将正确的产品送达正确的地点，且产品无缺陷、无损坏、数量正确、文档无误。当然，供应商不可能提供质量100%完美的产品，一定存在可能的误差范围。进行盘点时，买方必须检查整个批次的质量，挑出残次品。对于进口产品，把残次品退还给千里之外的供应商是不可行的。残次品将被送至内部维修点或当地市场进行维修，并在返修后进行部分延期交货。

供应链利益相关者协调并整合其业务流程，以尽可能低的成本实现卓越的客户价值。传统库存模型的付款是在供应商发货或客户收货后立即进行的。实际上，买方以延期（即在买方卖出产品后）付款的方式向供应商预付了贸易信贷。贸易信贷指的是允许在购买和结算之间存在一段时间的付款延迟，具体由买方和供应商共同商定。付款条件受双方之间的产品服务协议约束，不会中断物料流。贸易信贷是一种能使供应链合作伙伴双赢的策略。通常，贸易信贷由供应链层次结构中较高级别的伙伴（如供应商）提供给较低级别的伙伴（如买方）[1]。通过分别使用销售价格和购买成本进行计算可知[2]，买方的机会收益（赚取的利息）更好，而供应商的机会成本（付的利息）更差。除了由于延迟付款而带来的机会收益外，买方继续出售商品，获得客户的付款，但不偿还给供应商[3]。另一方面，供应商将贸易信贷视为一种竞争策略，以最大程度地提高销售额并减少现有库存。对于供应商而言，机会成本与财务收益之间需要权衡。库存管理就是要在相互矛盾的目标之间做出权衡。贸易信贷是一种非常成功的策略，通过这种策略，企业可以最大限度地提高销售额，进而获得利润。机会成本和机会收益被合并到利润计算模型中。

库存模型是围绕各种假设而建立的，并没有考虑这些假设的实际意义。Ahmed和Sarkar [4]指出，供应链的基础之一是管理从初始来源到最终客户的质量完美的商品。模型的假设之一是，一个批次内收到的所有产品都具有完美的质量。如今，企业希望能够保证供应、质量和安全性[5]。下一代制造业有望在生产中增加弹性，实现大规模定制，提高质量和生产率[6]。Khanna等[7]提出了一种针对残次品的最优补货库存策略。由于系统缺陷，所有零件均经过了100%的检查过程。据Tiwari等[8]的研究，绿色生产系统和返工过程通常是不完美的。此外，买方收到产品后立即向供应商付款。研究人员批评了这种不切实际的假设，敦促库存模型应以实际参数为基础[3]。本文提出的模型放宽了这些假设，以找到现实生活中问题的最佳解决方案。该模型扩展了以下内容：不合格产品的识别和修理、返工后的部分产品延期交货，以及多种贸易信贷政策。一种基于代数方法的算法被开发出来以实现利润最大化[3]。该方法提供了一个闭环的最佳解决方案。代数方法以最佳和最简单的方式解释了库存理论，同时最大程度地降低了出错的可能性。

本文旨在衡量将残次品返工并部分延期交付到物料流和利润系统中的影响，此外，也评估了多种贸易信贷对利润的影响。本研究为家用电器供应链（如日用电器）的管理人员提供了实用的见识。通常，这类公司会根据预期需求从海外供应商处获得库存，而任何超额需求都将被延期交付。但是，退回或更换损坏的产品并不划算。文章随后的内容组织如下：第二部分为文献综述；第三部分描述了所提出的数学模型的问题定义和假设；第四部分阐述了数学模型；第五部分用数值示例和结果验证模型；第六部分详细介绍了该模型的敏感性分析；第七部分提供了管理方面的见解；第八部分讨论了未来模型的扩展，作为结语。

2. 文献综述

现代库存模型是基于Harris [9]给出的经典经济订货量（EOQ）模型。基于某些假设，该模型可用于确定最佳订单的大小。库存管理领域的一些研究人员批评这些假设是不切实际的[3,10]。Goyal [11]通过引入一个允许延迟向供应商付款的库存模型，放宽了即时付款的假设。Porteus [12]认为批量生产过程可能会“失控”（out of control），从而导致出现残次品。Rosenblatt和Lee [13]发现产品质量和批次大小之间存在显著关系；他们认为缩减批次可以降低出现残次品的可能性。Salameh和Jaber [14]认为，残次品仍然具有价值，因此必须在返工后被重新使用。他们通过从批次中随机抽取残次品，扩展了残次品的经济生产量（EPQ）模型。通过在筛选总批次过程中研究残次品和缺货状况，Roy等[15]扩充了有关库存模型的文献资料。缺货可能由残次品引起，因此，一部分需求由部分延期交货满足。

随着时间的演变，关于生产和库存模型的研究文献也越来越多。研究人员通过放宽库存模型假设和整合库存管理的多个维度来扩大讨论范围，从而使库存模型更加实用。Eroglu和Ozdemir [16]引入了一种扩展的库存模型，他们假设所检查的每个批次都有残次品，以延期交付的形式应对缺货。后来，Sarkar等[17]提出了一个单阶段的经济生产模型，该模型认为残次品的不合格率是随机的。该模型引入了一种流程，用于对残次品进行返工或维修，并进行延期交付。Sarkar和Saren [18]引入了一种模型，该模型假设了一种筛选策略、筛选错误的数量以及非筛选产品的担保成本。他们发现，在100%检验的情况下，筛选成本会显著增加库存成本。Jaber等[19]也扩展了库存模型，用价格较高的本地应急采购品来替换残次品。Lashgari等[20]引入了一种库存模型，该模型在以下三种情况下向下游买方进行部分延迟付款，向上游供货商进行部分预付款：不缺货、完全延期交付和部分延期交付。通过对残次品使用经典优化技术， Sarkar等[21]提出了一种综合模型，该模型假设了两个阶段的检查、可变的运输成本和固定的返工成本。Ahmed和Sarkar [22]指出，以商业规模使用可再生产品，对于设计合理的供应链来说是必不可少的。因此，必须改进和规划经济的供应链。Kim和Sarkar [23]开发了一种多阶段去除器生产系统，通过在制造过程中去除所有残次品来提高质量。他们在单阶段制造过程中使用Porteus [12]的对数表达式来改进质量。

关于不完美的生产和库存模型的最新研究已经整合了库存决策的多个方面，如环境问题、预防性维护和不确定的需求。智能制造可能通过机会性过程计划以及复杂供应链的调度和控制进行无缺陷生产[24]。当然，有效的信息共享可以提高生产质量、产品可靠性、资源效率以及报废产品的可回收性[25]。但是，即使在当下，生产系统也无法提供100%完美的产品。Tiwari等[26]提出了一个单供应商/单买方系统的库存模型，该模型在运输、仓储和存储过程中存在残次品和碳排放。Taheri-Tolgari等[27]研究了生产系统中的残次品和预防性维护，以便在不确定的条件下建立筛选策略和最佳库存水平。Tayyab等[28]在多阶段生产模型中研究了残次品和产品需求不确定的影响，并且使用模糊理论和重心方法分别处理需求不确定性和消除目标函数的模糊性。Wook Kang等[29]提出了包含筛选、残次品、返工和计划延期交付的单阶段制造模型。这一分析方法用于找到最佳的批量大小和预估延期交货情况。Dey等[30]开发了一种用于两级生产系统的模型，以通过投资来降低缺陷率和安装成本。

供应链合作伙伴在其业务运营中进行协作，以获取或维持全球市场上的竞争优势。贸易信贷政策已成为国际上的最佳做法，也是维持伙伴关系的双赢策略。许多研究人员放宽了对即时付款的假设，并估计其对库存管理、销售和利润的最终影响，从而扩展了库存模型。例如，Soni和Shah [31]针对部分需求不变、部分依赖库存的零售商，以及提高多期贸易信贷的供应商制定了最优订购策略。Sarkar等[32]讨论了多层次贸易信贷的可持续性问题，并提出了一次准备多次交付的政策。他们的模型改善了三级供应链在经济和环境上的绩效。Yang和Tseng [33]提出了一种模型，即在可控制的交货期内，在允许贸易信贷和延期交付的情况下，实现多级供应链利润的最大化。近来，通过研究衡量质量缺陷、延期交货、返工、贸易信贷和多贸易信贷等多种实践的影响，将与库存模型相关的文献推向了新的高度。例如，Taleizadeh等[34]通过研究残次品、上游和下游贸易信贷以及延期交付需求的影响，改进了库存模型。Tiwari等[35]确定了在不同的允许延迟付款的情况下，库存模型中可能发生的潜在情况。Mohanty等[1]提出了一种集成残次品和贸易信贷的买方-供应商库存系统，以降低准备成本和缓解缺货情况。Taleizadeh等[36]开发了一种制造多种产品的单机系统，并假设存在残次品，允许贸易信贷。该模型可以为每种产品的周期长度、生产数量和延期交货数量求得全局最优解，从而使总成本最小化。Tiwari等[8]和Lashgari等[37]为非立即变质品制定了一种包含多期预付款和延迟付款时间表的订货策略。Zia和Taleizadeh [38]通过将延期交付与结合订单量的混合支付策略集成来刺激销量，进一步丰富了EOQ模型。Lashgari等[39]开发了一种易腐产品的库存控制模型，研究了在有限时间内与订单数量相关的贸易信贷的影响。表1总结了不同研究人员的研究成果，并将它们与本文提出的模型进行了比较[1,11-21,23,26-31,33,34,36-43]。

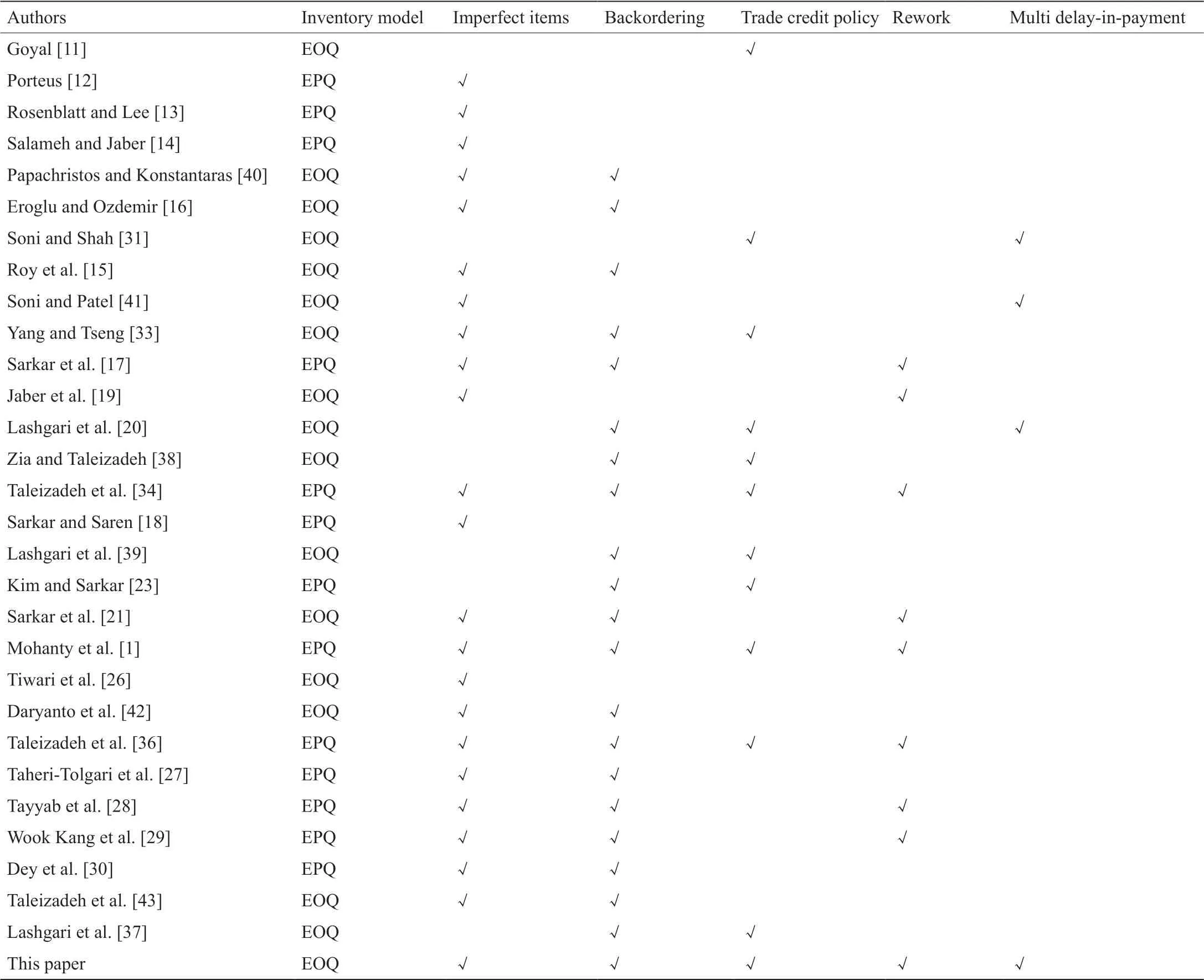
表1 库存模型的类型和综述

Taleizadeh等[43]开发的库存模型包含残次品和部分延期交货商品。在收到延期交货的商品时他们考虑了三种情况：第一种，刚好在库存水平等于零时收到；第二种，收到时交货数量等于残次品数量；第三，在仍然存在缺货时收到。Taleizadeh等[44]考虑了第四种情况，进一步扩展了库存模型，即当库存水平过高时收到延期交付的产品。Sarkar等[3]和Ahmad等[45]分别研究了由Taleizadeh等[44]在多信贷期限下提出的第二种和第四种情况。Taleizadeh等[46]开发的EOQ模型包含概率补货间隔和允许延迟付款的部分延期交货。Taleizadeh等[43]介绍了在部分延期交付情况下三种不同的残次品补货方案，并研究了它们对成本最小化的影响。没有一个系统是完美的，因此一个批次中将有一部分产品是残次品。当供应商的位置距离买方较远时，如在全球供应链中，此问题将变得更加严重。本研究的目的是衡量在多期付款延迟情况下第三种情况对利润的影响。

3. 问题描述和假设

这一部分阐述了本研究中的问题和假设。

3.1. 问题定义

在全球供应链中，买方管理者从位于数千英里之外的供应商处采购产品，想要得到100%完美的产品几乎是不可能的。产品在生产过程中也可能具有内置缺陷。同样，在全球运输过程中因处理不当也可能会造成损坏。在产品盘点过程中，买方会筛选出一定比例的不合格品。因为将有质量缺陷的产品退还给位于数千英里之外的海外供应商进行维修，既不可行也不划算，所以假定这些产品可以在当地维修。维修后的产品将通过部分延期交货的形式返回到初始库存中。在这里值得注意的是，原始库存的储存成本要少于返工产品。维修成本主要包括两个主要成本，即可变成本和固定成本。可变成本包括每个残次品的单位运输成本、原材料成本、工人费用以及返工产品在维修点的存放成本。固定成本包括本地商店的准备成本和运输成本。返工产品增加到初始库存中的时间会对库存产生重大影响，从而影响客户服务水平。在本研究中，假设返工产品会在库存短缺时重新进入买方库存，并且返工产品的数量等于缺货量。此外，假定供应商已允许买方执行多期付款延迟政策。换句话说，买方将在多个时期内收获不同水平的机会受益。需要设计一种有效的库存管理模型，该模型可以通过整合多期延迟付款和部分延期交货，用周期时间中乐观库存水平的比例（F）和周期时间（T）来优化批次大小（Q），从而最大程度地提高利润。残次品返工的库存系统流程如图1所示。

3.2. 假设

我们基于以下假设构建了数学模型：

（1）只涉及一种产品。

（2）收到的产品可能包含残次品。

（3）系统允许短缺，即只交付了部分产品。

（4）买方从全球供应商那里收到产品，将残次品寄回给供应商的成本高于在当地维修点修理的成本。

（5）筛选率和需求率是已知且恒定的。

（6）需求满足和筛选过程并行进行，但是筛选速度比需求速度更快（x＞D）。

（7）残次品有轻微缺陷，可以在当地进行维修。

（8）残次品率是已知的。

（9）买方采购成本Cu与买方出售价格P之间的相关性由P≥Cu给出。

（10）返工产品的持有成本高于完美产品的原始持有成本（hr＞h）。

（11）一旦缺货数量等于残次品数量，立即返还返工产品。

图1. 残次品返工的库存系统流程。

图2. 残次品库存情况以及返工产品返回库存。IMAX：最大库存水平。

4. 数学建模

本节将开发和解释一个总利润的同化库存模型，包括部分延期交货、残次品的维修和多次付款延迟，如图2所示。在时间的F部分，库存水平为正，等于F1+F2。其中F1= (1-β)F且F2=βF，β表示残次品的比例。系统的正库存水平为FT，其中T表示周期时间。Fi(i= 1,2)在[0, 1]。如果F等于0，那么所有需求将会失去，而如果F恰好等于1，则不会发生短缺。本研究中状态库存水平为FTD。初始批次在ts=FTD/x时以速率x接受筛选。筛选速度大于需求速度（x＞D）。在筛选期ts之后，从库存中取出质量为βFTD的残次品并运输至维修点。在间隔tR之后，返工的产品被返回买方的仓库。tR是运输和返工时间的累积时间。当地维修点的返工活动遵循控制协调。维修点的固定成本是sr+2A，其中sr是维修点的准备费用；A是运输的固定成本。残次品的可变成本由clm+ 2ct+hstR给出，其中clm是雇佣和材料成本；ct是运输成本；hs是维修点的持有成本；tR是总维修时间，包括运输、返还和修理。维修期限为tR=tT+FTD/R。当地维修点的总成本为sr+ 2A+βFTD(clm+ 2ct+hstR)。如果hr是返工产品的持有成本，而h是初始的单位持有成本，则h＜hr。随着残次品的返工，库存系统中出现短缺。假定当短缺水平等于返工产品的数量时，返工产品回到库存系统。最终，库存水平变为0。在提出的案例中，当短缺数量等于残次品数量时，每个周期的订货量为Q=F1TD+γF2TD+γ(1-F)TD=F1TD+γ(1-F1)TD，其中γ是延期交付的需求比例。

4.1. 订购成本

在单个周期T中，买方支出的单笔定购成本，用OC表示，其中O是固定订购成本。具体可表示为：

4.2. 筛选成本

整个批次的筛选成本SrC可表示为：

式中，单位检验成本为Cs；F是具有正周期的库存长度；D是需求率。

4.3. 持有成本

完美商品的持有成本和返修产品的持有成本的总和就是总持有成本HC，可表示为：

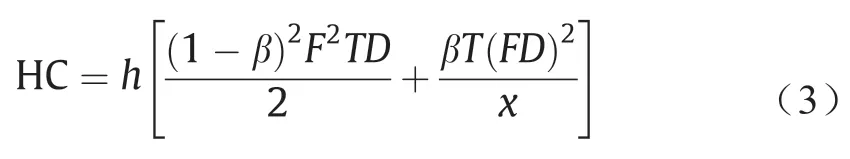
4.4. 维修成本

如果每单位维修费用的边际成本为m，则每单位的维修成本cR可表示为：

当短缺数量等于残次品数量时，就会返还返修产品，因此，库存变成βFTD个单位。随着周期的结束，系统的短缺水平变成(1-F)TD。对于给定的周期，订购的数量可表示为Q=FTD+γ(1-F)TD。

4.5. 短缺成本

短缺成本SC可表示为：

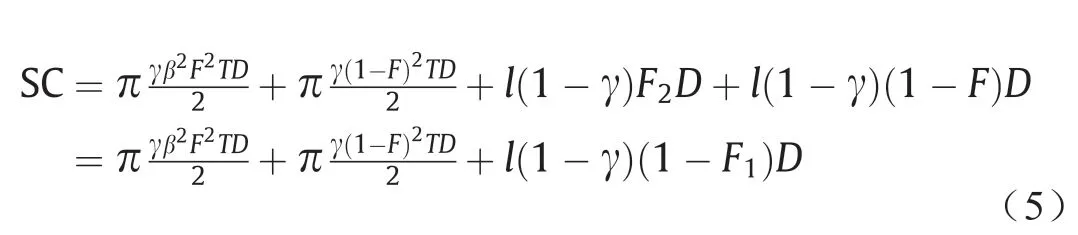
式中，π是延期交货成本；l是销售损失成本；γ表示延期交货需求的百分比。

4.6. 商誉惩罚成本

商誉惩罚成本GWC可表示为：

式中，w是交付给顾客的残次品百分比；v是退还产品的成本；g是商誉损失带来的惩罚性成本。

4.7. 收取和赚取的利息

在允许延迟付款的策略中，如果付款期限长于交货期限，那么买方会获得额外的利息收入。如果付款期限小于交货期限，那么买方获得的利息收入较少，需要支付更多的机会成本，而供应商只需支付更少的机会成本以获得利息收入。因此，供应商的模型有两个后续案例，分别由允许的付款时间和交货时间的长度确定。这两种预期情况的成本差异如下：

情况1：如果交货时间T等于或小于允许的付款时间M，则仅赚取利息收入，因为在这种情况下收取的利息为零。这种情况如图3所示，具体可以表示为：

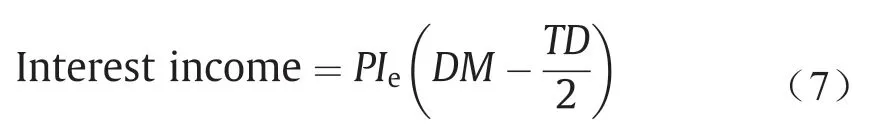
式中，P是销售价格；Ie是赚取的利息。

情况2：如果交货时间T大于初始允许的付款时间M，并且等于或小于随后允许的付款时间N，则将收取利息并赚取利息。这种情况如图4所示，可以写成：

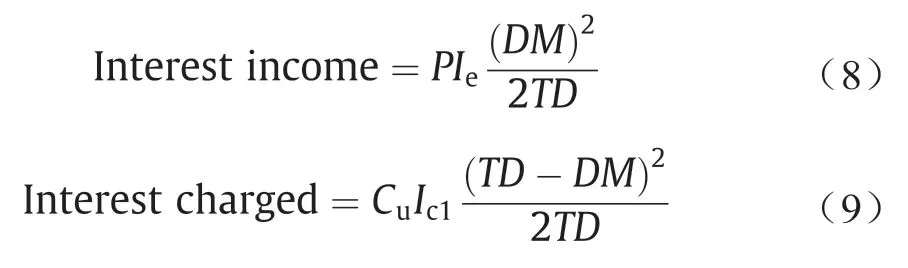
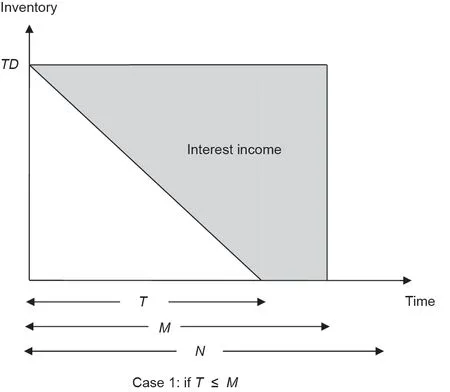
图3. T ≤M时的利息示意图。

式中，Ic表示收取的利息。

情况3：还有一种特殊情况，如果买方未能在初始允许的时间内支付所需的款项，则会被收取额外的利息。在这种情况下，交货时间T大于随后的可允许付款时间N。这种情况如图5所示，并可表示为：

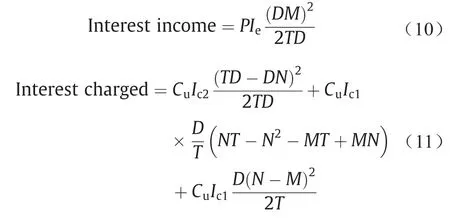
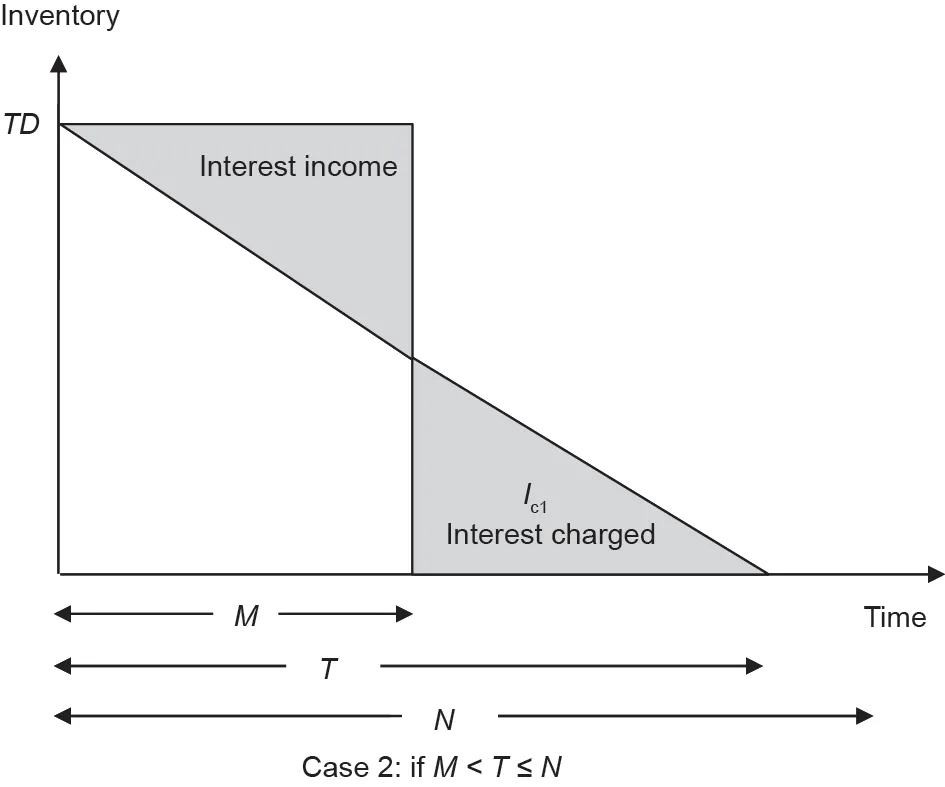
图4. M＜T≤N时的利息示意图。

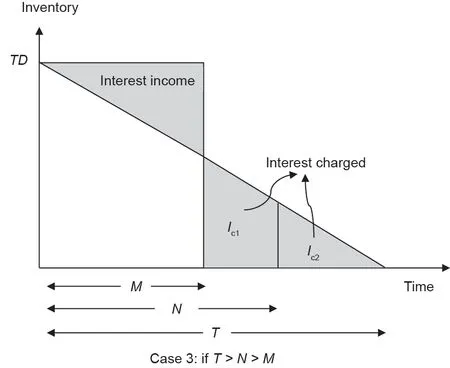
图5. T＞N＞M时的利息示意图。

利润总额函数：利润总额=销售价格-（订购成本+产品成本+筛选成本+持有成本+维修成本+短缺成本+商誉惩罚成本+赚取的利息+收取的利息）

在上述多期付款延迟的情况下，我们讨论了三种情况，这三种情况的总利润方程式为：

情况1：总利润公式将是公式（1）～（6）和公式（7）的组合，其中交货时间T等于或小于允许的付款时间M，从而导致赚取利息和收取零利息，即T≤M时，总利润TP1为：

式中，u是残次品的退款成本。

情况2：总利润公式将是公式（1）～（6）和公式（8）～（9）的组合，其中交货时间T大于初始允许付款时间M，等于或小于随后的允许付款时间N，导致收取和赚取利息，即M＜T≤N时，总利润TP2为：

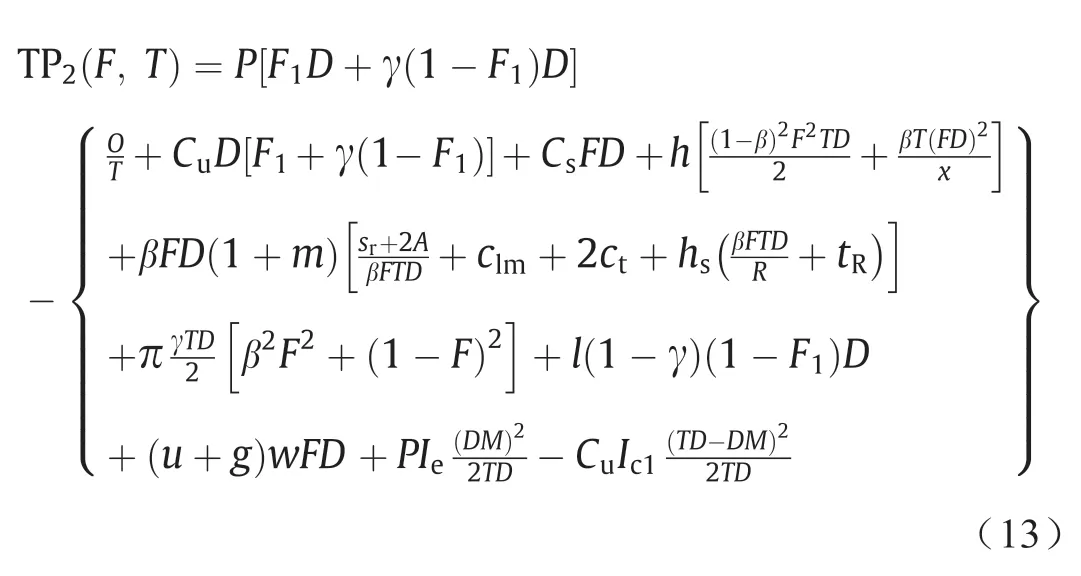
情况3：总利润公式将是公式（1）～（6）和公式（10）～（11）的组合，其中如果买方未能在最初允许的时间内支付所需的款项，则会被收取额外利息，即T＞N＞M时，总利润TP3为：

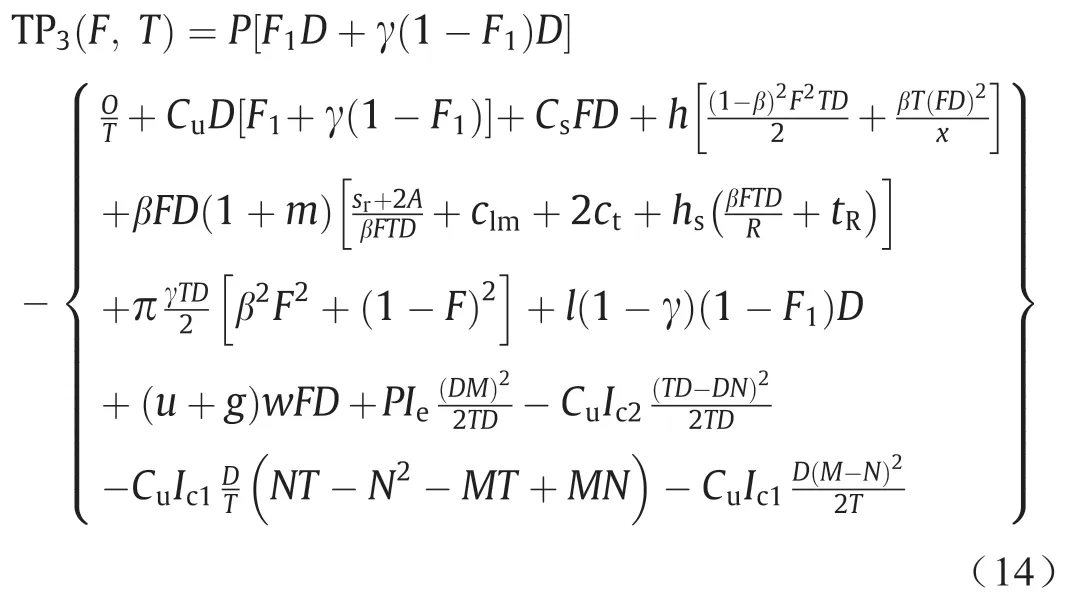
4.8. 具有最佳T值和F值的情况1

根据公式（12），情况1的利润公式可以表示为：

因此有F1+γ(1-F1) = 1 - 1 +F1+γ(1-F1) = 1 - (1-F1)(1-γ)，则利润函数可以被表示为：

代入Cz=P+l-Cu，总利润函数可表示为：

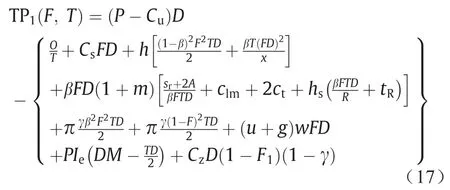
另外，公式可以被精简为：

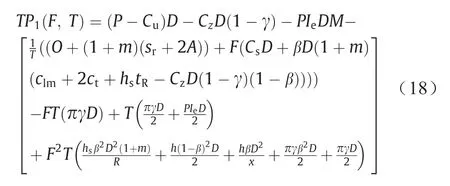
式中，D(P-Cu) -CzD(1 -γ) -PIeDM是常数项。如果总成本最小，那么总利润最大。如果考虑F1= (1-β)F，则Y(T,F)可以写成：

精简后的Y(T,F)公式可以写成：

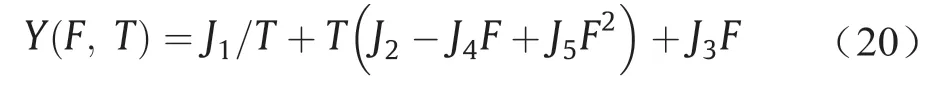
J1～J5的值请参见附录A中的第1节。

公式（20）可以重写成：

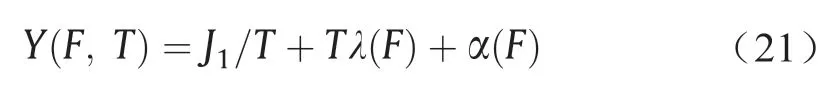
式中，λ(F) =J2-J4F+J5F2=J2- 2J2F+J5F2且α(F) =J3F。

当以下条件成立时，成本公式相对于T取最小值（详情参见[15]）。

如果在以下成本函数中替换T*，则总成本最低。

T的最优值可能取决于F。采用非微分方法得出F的最优值。已开发的公式结构仅处理包含决策变量的函数部分，并可表示为：

替换公式（24）中的J4、J3和J5，可知

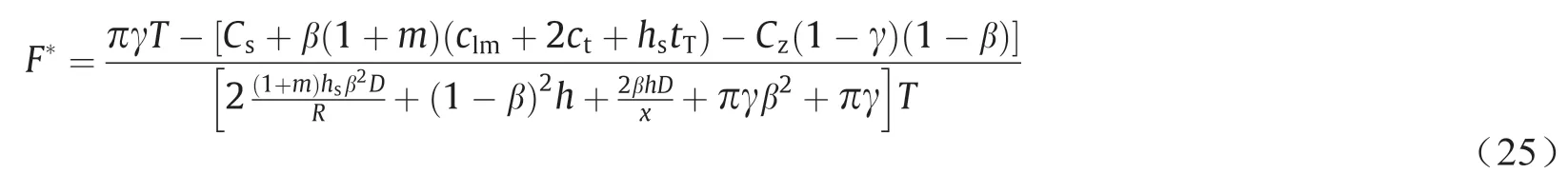
由公式（22）得

将最优的F值代入公式（26）得

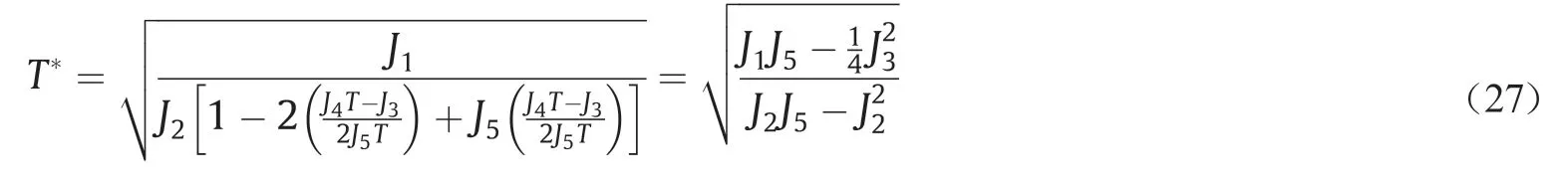
最后，将J4、J3和J5代入公式（24）得

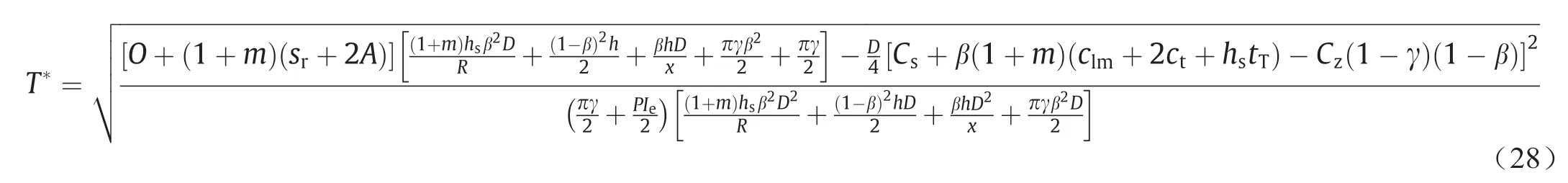
4.9. 具有最佳T值和F值的情况2

根据公式（13），情况2的利润公式可以表示为：

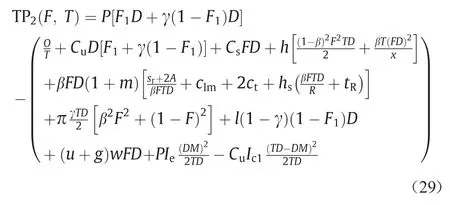
F*和T*采用最佳值（见附录A第2节）：

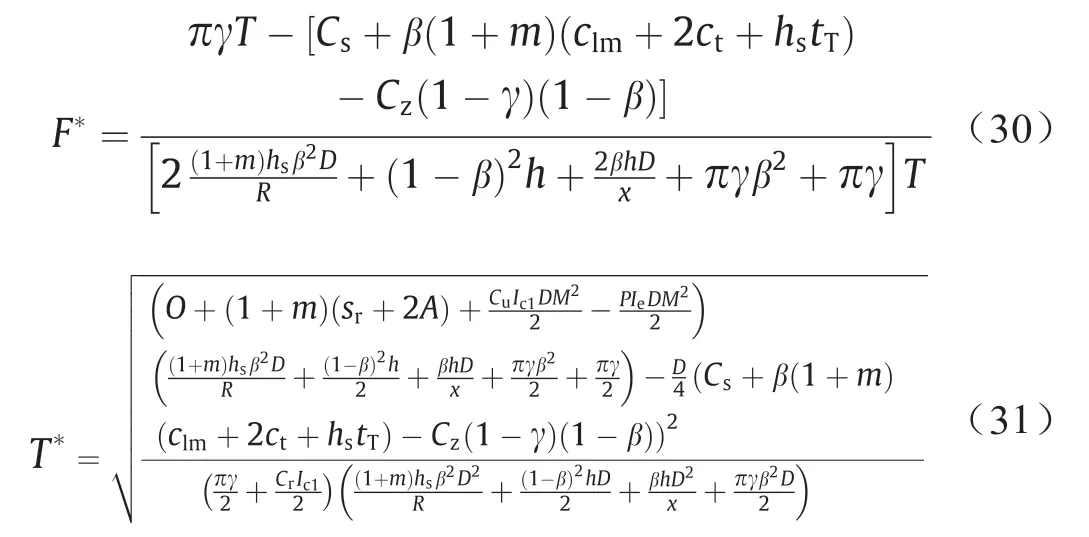
4.10. 具有最佳T值和F值的情况3

根据公式（14），加上订单数量+1和-1的情况，情况3的利润公式可以表示为：

F*和T*采用最佳值（见附录A第3节）：

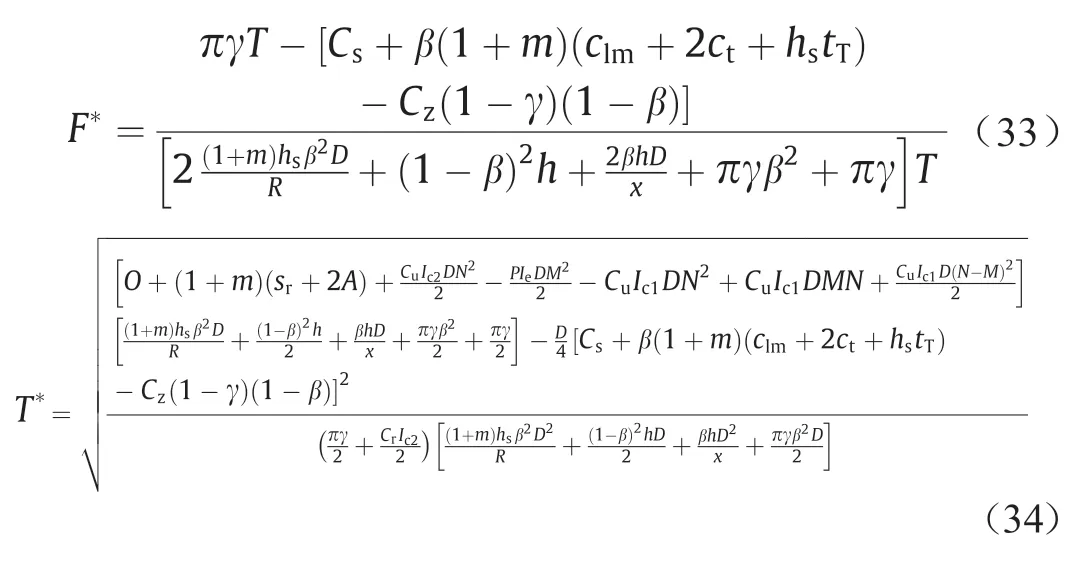
5. 数值实验

本节描述数值实验。表2和表3展示了实验数据和每种情况下最优解中每个利润变量和决策变量。数据来源于Taleizadeh等[36]的研究，并加入了Sarkar等[3]的销售损失、退货成本和延期付款等其他参数。图6展示了各种情况下的最佳解决方案。

表2 实验所用数值

表3 不同情况下的最优成本

该解决方案表明，当周期时间等于一年的0.050，乐观库存水平为0.68%，且订购的产品数量为2550时，情况1的最佳状态出现，此时总利润为1 204 220美元。在这种情况下，周期时间等于或小于第一允许的付款期限。对于情况2，当周期为一年的0.082时，达到最佳状态，该期间的乐观库存水平为0.73%，产品订购数量为4150，总利润为1 201 270美元。在这种情况下，周期时间大于第一允许的付款期限，并且小于或等于第二允许的付款期限。对于情况3，当周期时间为一年的0.124时，可达到最佳状态，该期间的乐观库存水平为0.75%，订购的产品数量为6250，总利润为1 194 630 美元。在这种情况下，周期时间大于第一和第二允许的付款期限。显然，情况3提供的利润最大，情况1提供的利润最少。

这些结果证明，如果供应商给买方的允许期限等于或大于周期时间，则利润较小；而如果小于周期时间，则利润较大。买方从销售商品和赚取利息中获利，并从中受益。周期时间的最佳结果是使用某些参数获得的，但是，乐观库存水平F可能会发生变化，并且必须维持在[0, 1]。如果F等于零，则将失去所有需求。相反，如果F等于1，则不会发生短缺。如图7所示，在所有情况下，延期交付需求的增加都会增加总利润。此外，值得注意的是，在所有情况下，增加单位持有成本都会降低总利润，如图8所示。如果单位持有成本过高，则无法满足最优解决方案的允许期限。下面进一步分析展示了多个波动因素对总利润的影响。

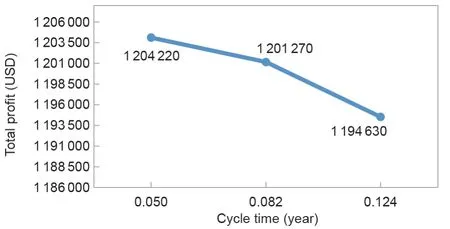
图6. 不同情况下的最大利润。

图7. 不同情况下延期交付需求的变化对利润的影响。

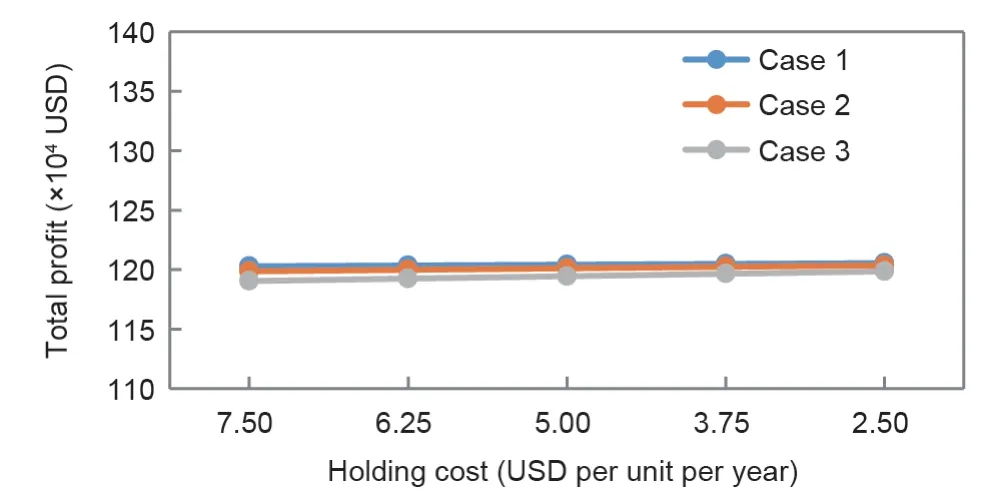
图8. 不同情况下持有成本的变化对利润的影响。

6. 敏感性分析

图7至图9和表4展示了案例中关键参数变化对总利润影响的敏感性分析。这些参数包括：持有成本h、运输成本ct、维修所需的人工和材料成本clm、残次品退还的百分比w、每年每美元赚取的利息Ie、第一期收取的利息Ic1、第二期收取的利息Ic2、延期交付成本π、延期交付需求γ、第一允许延迟期限M和第二允许延迟期限N。结果表明，持有成本h值的变化会导致每种情况下的TP产生较小的逆变化，以显示平衡状态。结果还表明，总利润对h的正负变化同样敏感。类似地，残次品往返于修理点的固定运输成本ct、维修所需的材料和人工成本clm以及残次品返还的百分比w，在三种情况下都对总利润产生微小但反向的变化。每年每美元赚取的利息Ie的变化导致三种情况下TP出现微小但正向的变化。结果表明，TP在平衡状态下与Ie显著正相关。收取的利息Ic1的变化对情况1无效，类似地，Ic2对情况1和情况2无效，因为在这些情况中不收取任何利息。变化模式中存在平衡状态。每种情况下，延期交付成本π的变化都会导致TP出现微小但反向的变化。每种情况下，延期交付需求γ的变化都会导致TP显著变化。第一允许延迟期限M值的变化仅导致情况1和情况2中的TP出现边际变化。因此，该参数没有显示出平衡状态。第二允许延迟期限N的变化仅导致情况2和情况3中的TP变化。

表4 关键参数的敏感性分析

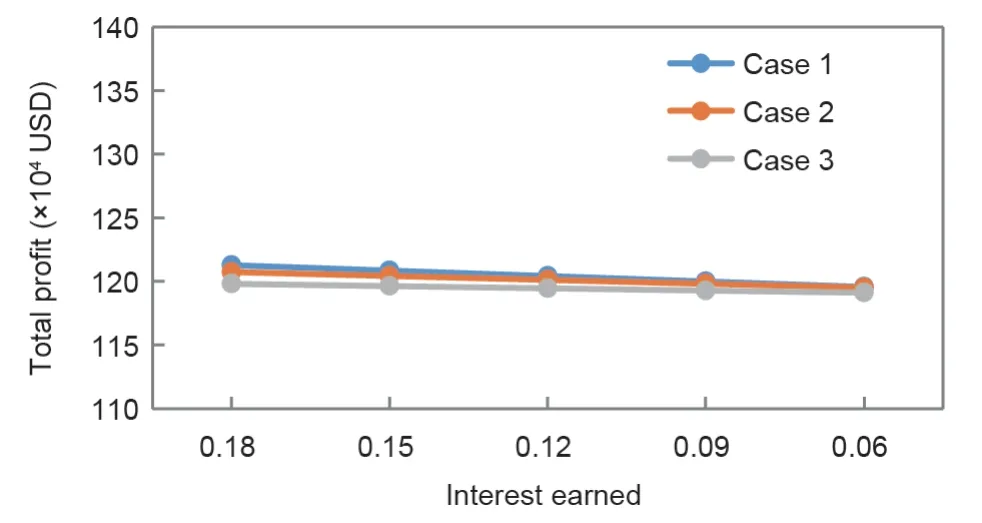
图9. 不同情况下赚取利息的变化对利润的影响。

7. 管理见解

本研究为残次品库存、当地商店中残次品的维修以及多贸易信贷期限框架下的行业经理提供了重要的见识。在周期时间大于供应商给予买方的多个延迟付款时间的情况下，可以使总利润最大化。公司经理必须决定乐观库存水平比例和周期时间。因此，参数之间的权衡对于获得持久的业务回报是必要的。这项研究还通过变动参数对总利润进行了深入分析，这些参数包括延期交付的部分需求、维修点的材料成本、支付的利息、赚取的利息、单位持有成本以及残次品的运输成本。

此外，如果卖方并非来自当地，这项研究也为企业处理不满意的产品提供了一条途径。这些残次品仍然很有价值并且可以被修复。为了获得最大利润，管理人员必须优先考虑可接受的延迟付款期限政策、周期时间和部分延期交付需求。管理人员必须通过衡量允许的延迟付款期限来提高销量，从而减少库存。通过系统地考虑主要参数的相互作用来控制它们可带来最大的收益。这项研究的结果为行业经理获得最佳方案提供了指导。

8. 结论

通过将部分延迟订购和多期延迟付款与库存结构整合，本研究引入了新的库存模型以适应残次品的维修。全球供应商的制造系统并不完美，并且会产生残次品。而且，维修好的批次也可能包含残次品。考虑到制造商的距离较远，买方必须使用逆向物流来替换残次品，但是这种方式既费时又需要花费较高的成本。事实上，这些残次品仍然很有价值，只需要在当地的维修点进行维修即可。与将产品寄回给全球供应商相比，本文所提出的解决方案还将对环境产生积极影响。在这种情况下，通过允许在本地维修点修复最终产品的缺陷，本项研究提出的框架扩展了包含残次品的库存模型的现有知识体系，从而最大程度地减少了销售损失，缓解了部分延期交付情况。返工后，已修复的产品将重新集成到初始库存系统中。当缺货需求等于从当地维修点收到的残次品数量时，返还已修复的产品。研究中提出的模型还将库存系统与贸易信贷的最佳实践（在多期延迟付款方面）集成。这种最佳做法将为买方提供短期财务援助，并通过增加销售量使供应商受益，最终获得多个周期时间和多期延迟付款设置的最佳结果。采用非微分方法开发库存模型，目的是获得封闭式的结果，该方法已在先前的研究中得到有效的使用和验证。此外，在数值实验的帮助下，建立并验证了所提出的模型，同时还对关键参数进行了敏感性分析以支持管理决策。

本研究通过创建具有多期付款的策略并将其用于标记推测结果，以利用整个利润函数的基本属性。为了获取最大利润，没有考虑公司之间相互了解的情况。该研究还可能影响公司的短期现金流。从业人员可以通过在所需结算金额与可用资源之间取得适当的平衡来增加公司的营业额。如果无缺陷产品的主要持有成本大于第二允许延迟期限，那么获得最佳解决方案是不可能的。该模型通过调整多贸易信贷期限部分延期交货情况下的正库存时间和周期时间的比例，来提高全球供应商的可持续库存管理绩效。未来的研究可以通过测试双产品和双买方案例来扩展这些发现。在此模型中，提供新的无缺陷产品来代替返工产品也是未来研究的另一个方向。

Compliance with ethics guidelines

Waqas Ahmed, Muhammad Moazzam, Biswajit Sarkar, and Saif Ur Rehman declare that they have no conflict of interest or financial conflicts to disclose.

Nomenclature

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.eng.2020.07.022.