遗传算法与分组数据处理神经网络相结合的人工智能预测盾构掘进过程中滚刀的寿命

Khali Elbaz ，沈水龙,*，周安楠，尹振宇，吕海敏

a Department of Civil and Environmental Engineering, College of Engineering, Shantou University, Shantou 515063, China

b Key Laboratory of Intelligence Manufacturing Technology, Ministry of Education, Shantou University, Shantou 515063, China

c Discipline of Civil and Infrastructure, School of Engineering, Royal Melbourne Institute of Technology, Melbourne, VIC, Australia

d Department of Civil and Environmental Engineering, The Hong Kong Polytechnic University, Hong Kong, China

e State Key Laboratory of Internet of Things for Smart City, University of Macau, Macau, China

1. 引言

随着城市化进程的加速，中国城市正在建设越来越多的地铁系统[1-5]。盾构隧道是在各种地质条件下均可以建造地铁隧道的一种经济有效的施工方法[6-9]。在混合地层或岩石地层条件下，滚刀向前推动并通过推力（TF）压入岩石。通过增加滚刀切入的压力，岩石裂纹会出现并扩大。然后，由于相邻滚刀之间的裂纹聚结贯通，岩石被切割碎裂，从而压碎岩石。滚刀与岩石-土体之间复杂的相互作用会导致其严重磨损，而这是很难预测的[10,11]。在一些隧道工程项目中，滚刀的消耗和更换约占项目成本和时间消耗的三分之一[12]。为了评估机械化掘进过程的开挖成本，正确估计滚刀的寿命至关重要[13,14]。

滚刀的消耗很大程度上取决于地层条件、盾构操作参数和切割条件。解决关键问题有助于降低建设成本和提高开挖效率，如确定造成滚刀消耗的主要原因、分析磨损机理以延长滚刀寿命。已有研究通过对施工过程的试验研究[15-19]和经验或理论分析[20-22]，研究了地层条件对滚刀消耗的影响。例如，基于统计分析和经验公式，Hassanpour [23]提出了滚刀寿命与地质参数之间的关系。Ren等[14]提出了基于总能耗理论的非均质地层磨损预测模型。Yang等[24]基于兰州建设项目的数据，分析了输水隧道的滚刀的故障和消耗。许多参数都会影响滚刀寿命，所以经验模型的预测结果与测量结果并不完全匹配。因此，有必要开发能够更准确地预测异质地层中滚刀寿命的模型。

近年来，人工智能（AI）技术[如回归、优化和分组数据处理（GMDH）型神经网络（NN）]已在广泛的岩土领域中成功应用[25-28]。分组数据处理是一种自组织技术，可用于解决具有高度复杂性的非线性系统中的问题。该技术的主要优点是可以通过二次多项式估算解析方程。此外，分组数据处理技术提供了一种便利的工具，可以处理短而杂乱的数据[29,30]。但是，分组数据处理这类人工模型常常会陷入局部最小值问题，因此无法找到全局最小值。因此，必须使用主流的优化算法来避免此类缺陷。遗传算法（GA）是受达尔文理论启发的进化方法，可以增强人工模型的泛化性能[31-33]。

本研究的目的是通过AI技术以及地质和操作参数的输入数据，为滚刀的使用寿命提供可靠的预测模型。本文提出的混合模型首先用于预测滚刀的寿命。因此，本文建立的模型填补了非线性系统与机器学习技术之间的空白。为预测滚刀寿命，本文使用统计回归方法（线性和非线性）进行详细的试验分析。随后，本文开发了一种基于分组数据处理型神经网络与遗传算法集成的数学模型，以评估其滚刀寿命预测的性能。以中国的广深城际铁路项目为例，本文论证了该模型的可行性及其应用潜力。此外还对建立的方法进行了敏感性分析，以确定每个输入参数对模型输出的影响并促进评估程序。

本文的组织如下：第2节展示了研究背景，其中包括影响滚刀寿命估算的因素；第3节介绍了基本的分组数据处理型神经网络，并描述了模型的开发；在第4节中介绍并分析了项目概况、滚刀消耗和数据准备；第5节展示了结果和有关预测滚刀寿命的讨论；最后一节对本文进行了总结。

2. 背景

在隧道工程项目中，基于性能分析的滚刀使用寿命的预测至关重要，因为整个项目的成本和进度都是根据掘进效率确定的。这在大型隧道项目中尤其必要，由于盾构隧道施工是一个复杂的机-土之间相互作用的过程，并受各种参数的影响。因此，研究这些参数很重要，以避免在施工过程中产生许多不必要的损失和麻烦[34]。滚刀寿命的有效参数应视为建立精确模型的输入变量。

通常，在开挖隧道之前应事先对地质条件进行调查。盾构掘进效率与土体的性质和类型有关。单轴抗压强度（UCS）是反映岩石材料的强度特性的参数，文献[23]将UCS作为反映地质条件最具代表性的输入参数。盾构切入速率（PR）表示开挖过程中掘进距离与掘进时间之比，是盾构施工参数的关键输入参数之一[12,35,36]。在另一项研究中，Ren等[14]研究了推力对滚刀寿命的影响。推力表示施加于刀盘的荷载，是影响岩石破碎和刀具磨损的主要参数之一。掘进过程中施加在刀具上的推力表示为切入速率和岩石材料特性的函数[37]。由于作用于滚刀的力可通过操作参数估算，因此切入速率不仅取决于岩石材料特性，还受到切割条件的影响，切割条件同时直接影响滚刀的使用寿命[38-40]。比能（SE）是指开挖单位体积的土体所消耗的能量。Namli和Bilgin [41]指出，可以利用比能来评估隧道掘进机的切割效率。此外，刀具的旋转速度反映了切割过程中的岩石破碎状态，这直接影响掘进效率，进而影响切割性能。基于上述参数，值得注意的是，滚刀的寿命是受多个地质和操作参数影响的极其复杂的系统的输出。而且对盾构切割性能的分析仍然主要依赖于经验以及统计分析和理论分析。因此，系统分析方法可以利用盾构监测数据对盾构切割性能进行全面了解。

3. 人工智能方法预测滚刀寿命

3.1. 分组数据处理型神经网络

分组数据处理型神经网络是解决AI问题的最佳方法之一，如识别和预测复杂施工问题中随机过程的短期和长期预测。分组数据处理型神经网络是分层结构；每层包含独立的神经元，独立的神经元成对组织，每对神经元通过二次多项式积分。在所有网络层中，新神经元都是通过与前一层的独立变量交叉而形成的。因此，产生了新一代的神经元。Anastasakis和Mort [42]提出了一种分组数据处理方式，它基于选择最佳二次多项式公式来使用一组输入和输出变量对非线性模型进行建模。对于输入向量X= (x1,x2,x3, …,xn)，预计输出（）接近于实际输出（yi）。因此，观察到的多输入单输出数据对的M个指示如下[43]：

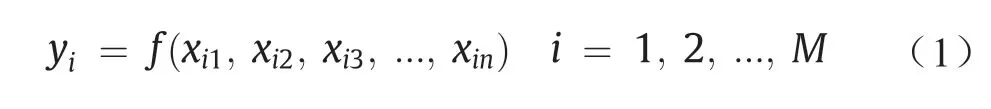
为了根据给出的输入向量X= (xi1,xi2,xi3, ...,xin)预测所需的输出（），预测的输出如下：

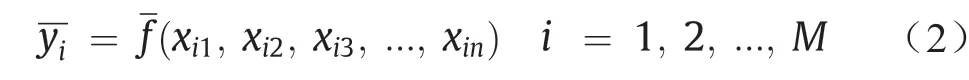
将实际输出与估计输出之间的平方方差相减以确定分组数据处理：

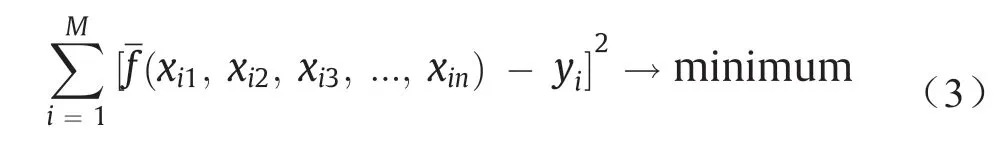
分组数据处理提供了输入和输出参数之间的全面映射，这些参数以非线性函数的Kolmogorov-Gabor函数形式表示[44]：

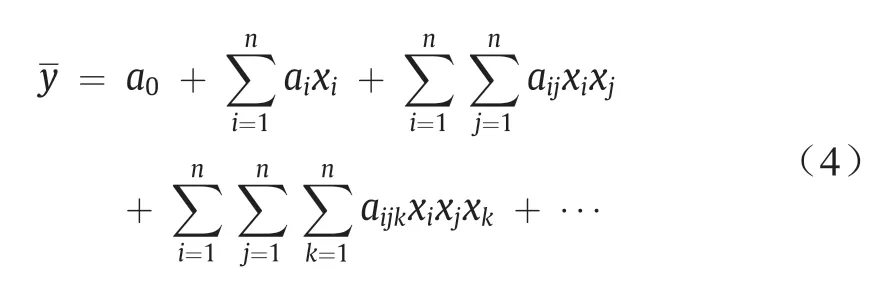
给出的公式是指Kolmogorov-Gabor公式，可以通过二次多项式形式表示：

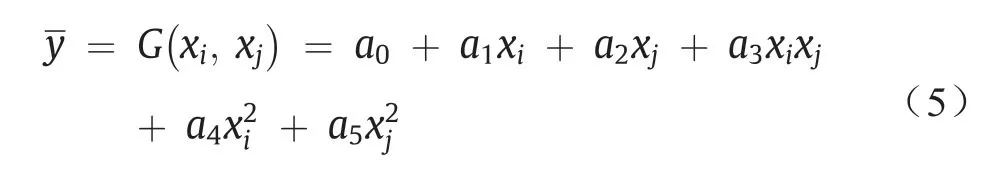
通过使用回归分析来最小化每组(xi,xj)作为输入参数的实际输出与估计输出之间的差异[45,46]，分组数据处理型神经网络可以用于估算方程式中的系数ai(i= 1, 2, …, 5)。

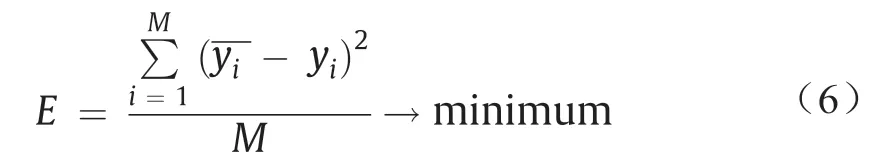
要显示分组数据处理方法的主要形式，即方程式的矩阵形式。式（5）可以重写如下：

式中，Y= {y1,y2, …,ym}T和a= {a0,a1, …,a5}，它表示二次多项式矢量的系数。根据各种p和q(∈{1, 2, …,n}）估计A：

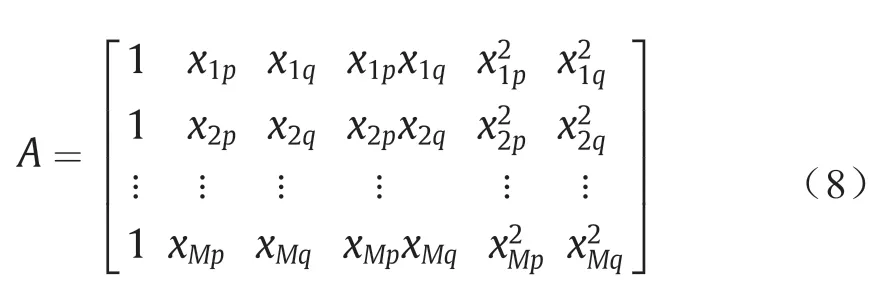
多元回归分析的最小二乘公式可求解一个正态方程：

等式（5）的最佳系数向量是根据M数据的三元组计算的。尽管分组数据处理模型提供了克服短数据和含噪声数据的便利工具，但它通常难以克服局部最优问题，因此无法找到全局最小值。

在计算部分描述系数后，根据目标函数（OF）调整选择标准，以消除得到较差结果的神经元。为执行选择步骤，将数据库分为训练数据集和测试数据集。每个输出的OF计算如下：

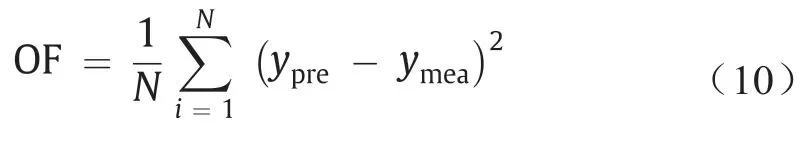
式中，ypre,ymea和N分别是预测数据集、测量数据集和总数。

根据测试数据进行选择步骤，并将每个输出的OF应用于评估过程。分组数据处理过程包括增加层次、计算部分特征系数以及消除引入最差结果的神经元。在训练阶段，最近网络层的输出将转换为下一层的输入。在选择阶段之后，如果存在一个神经元的现有层残差，或者添加新层的训练不会提高整个网络性能的情况，则此过程将中断。获得最佳行为的神经元保留在前一层中，其他神经元则被消除。最终，执行修整阶段以实现最终的网络结构。图1显示了分组数据处理过程。图中已移除的神经元以浅色显示[46]。参考文献[46]中提供了与分组数据处理型多项式网络有关的详细的数学推导以及其他背景信息。

3.2. 遗传算法

遗传算法是一种自适应启发式搜索技术。最初由Holland [47]提出，Goldberg [48]对其拓展以优化复杂问题，该算法是以达尔文进化论为基础建立的。根据此概念，适应性较低的种群往往会消失，而最适者会生存并产生新的后代。遗传算法以其简单、弹性和自适应的特点著称。遗传算法会针对个别解决方案反复调整种群。会随意选择近代的父母作为下一代生育子女的父母，直到种群达到最佳为止。对于每一代种群，根据强壮等级形成新的近似值集合。在每次迭代过程中，遗传算法会重复执行，直到满足终止标准（如预定义的迭代次数）。文献[48]提供了遗传算法的更多相关详细信息。尽管遗传算法广泛地应用于神经网络设计的不同阶段，但是它的本地搜索能力很差[28,49,50]。因此，有必要提出一种精度更高的模型，该模型通过在实现设计过程的同时调整设计参数来降低OF。本文提出了一种混合分组数据处理型神经网络模型，以解决上述模型的缺点，并在预测中产生协同效应，这已成为近年来的主要方法。

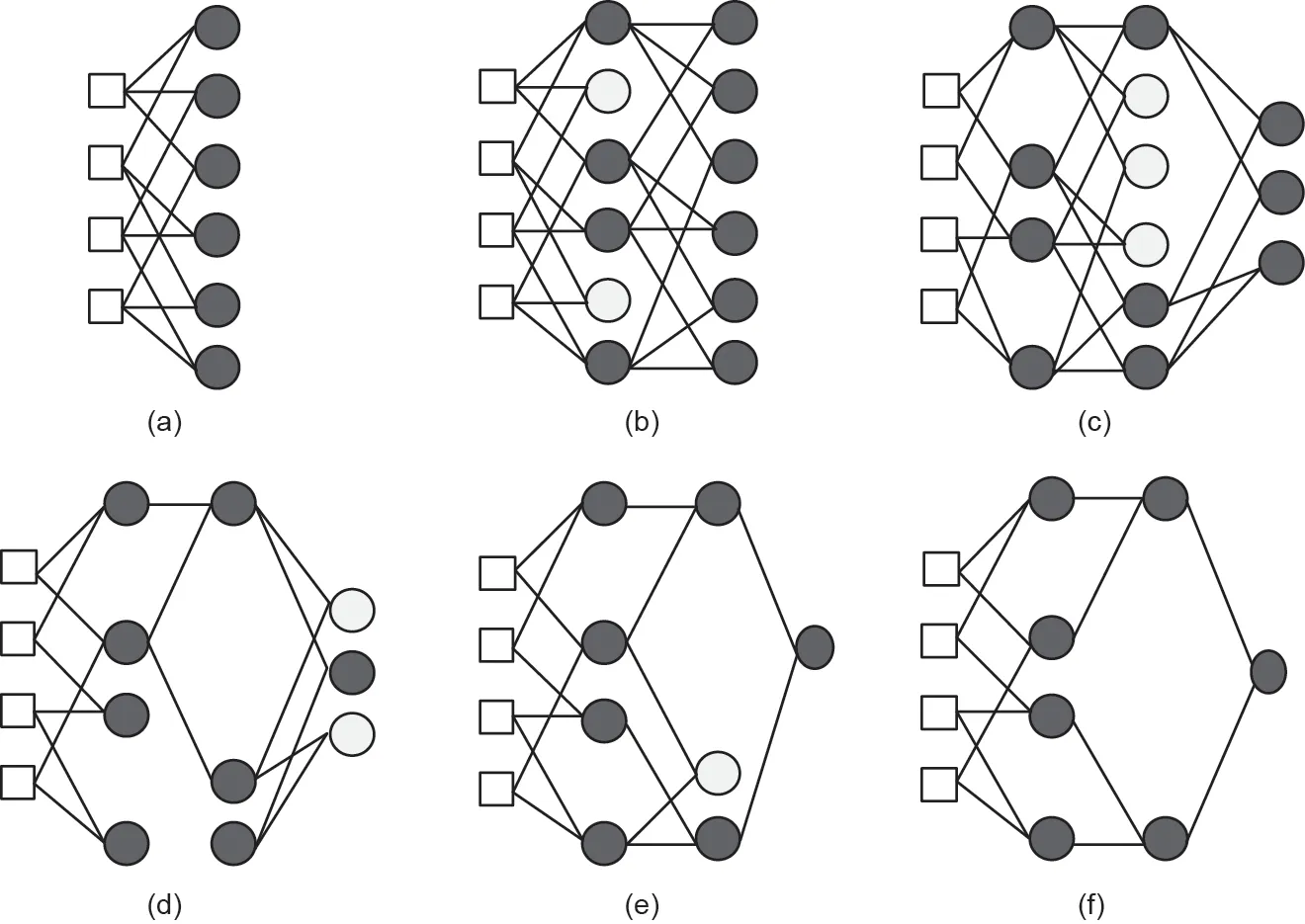
图1. 分组数据处理过程的图形示例。（a）由四个输入组成的网络层；（b）计算所有神经元的系数后，消除的神经元以浅色显示；（c）在新层上选择的神经元；（d）在选择过程结束之后，当任何一层都只剩下一个神经元时，训练停止；（e）和（f）删除所有不参与网络的神经元。在Elsevier Ltd.的许可下转载自参考文献[46]，©2012。

3.3. 基于遗传算法的分组数据处理型神经网络设计

为了更准确地预测滚刀寿命，本研究引入了一种混合型分组数据处理-遗传算法模型。在此混合模型中，上述遗传算法用于优化数据处理型神经网络的整体结构（即每个隐藏层的神经元数量及其相关性的形成，结合个体值分解以检测适当的最优系数）。图2为将数据处理与遗传算法模型集成在一起以预测滚刀寿命的流程图。该模型的实施步骤如下：

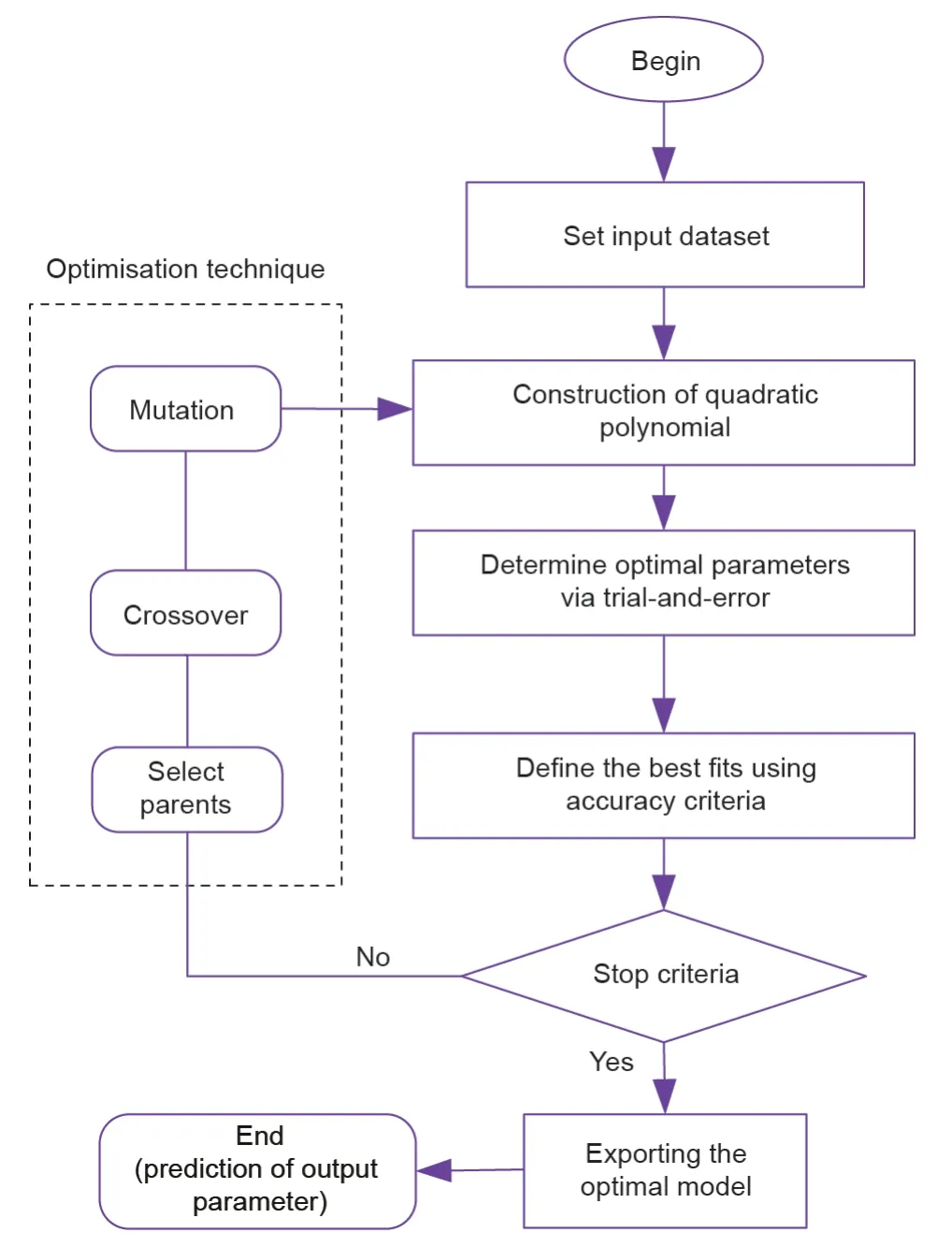
图2. 分组数据处理-遗传算法模型的广义结构流程图。

步骤1：对输入参数X= {x1,x2, …,xn}和相应的输出Y= {yn}进行预处理，以获得适合训练模型的数据集。

步骤2：将分组数据处理-遗传算法混合模型中使用的数据分为训练集和测试集。训练集用于训练神经元，而测试集用于评估神经元对数据预测的准确性。

步骤3：初始化种群，并生成遗传算法算子以优化分组数据处理参数。

步骤4：在选择阶段，根据适应度，识别出代表最佳解决方案的两条优选染色体，并将选定的染色体作为父代来创建子代、染色体和新生代。

步骤5：在交叉阶段，染色体以产生子代的特定概率随机杂交。

步骤6：通过变异，调整种群多样性，增强搜索能力，以克服局部最优解的收敛性。

步骤7：通过迭代处理，应用遗传算法直至达到预设条件。由于没有明确的方法或公式来选择最佳的遗传算法参数，因此本研究使用试错法估算遗传算法参数。以这种方式，在逐渐增加相对适应度函数的情况下进行了混合模型的试验，直到没有进一步的改善为止。

4. 案例描述

4.1. 项目总结

广深城际铁路位于中国广东珠江三角洲沿海地区，隧道全长22 km。该项目连接广州北站和深圳宝安国际机场。隧道段位于机场3号航站楼区域，宝安机场北站和宝安机场站之间。图3为本文研究案例位置，隧道长约3.3 km。利用土压平衡（EPB）盾构机施工。盾构机刀盘直径为8.85 m，拖尾护罩的直径为8.78 m。管片宽度为1.6 m，厚度为0.4 m。每环预制混凝土衬砌环（六个节段和一个键块）竖立在屏蔽体内，其内径和外径分别为8.10 m和8.50 m。对推力（TF）、刀盘转速（RPM）、螺旋机转速（SC）、扭矩（CT）、注浆压力（GP）、切入速率（PR）、埋深（H）、土体掌子面压力（SP）和比能（SE）进行实时监测。表1列出了EPB盾构机的规格。

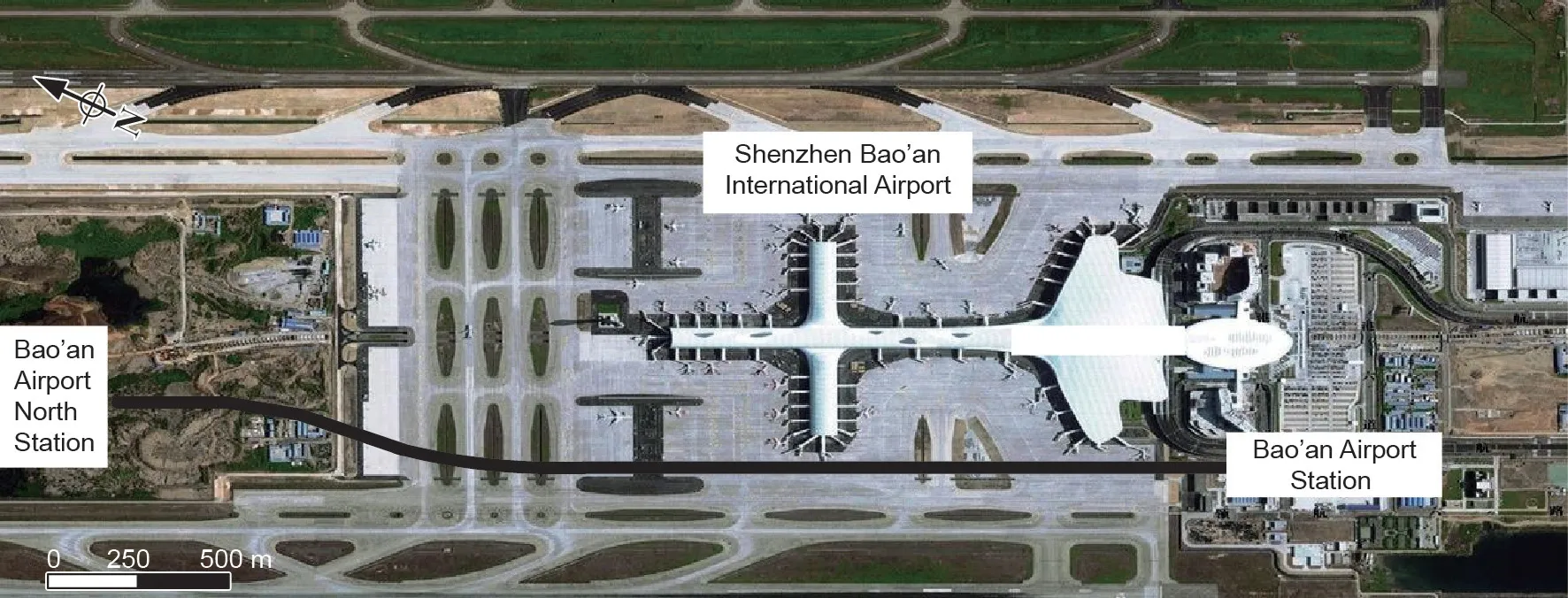
图3. 施工现场位置（基于Google Earth）。

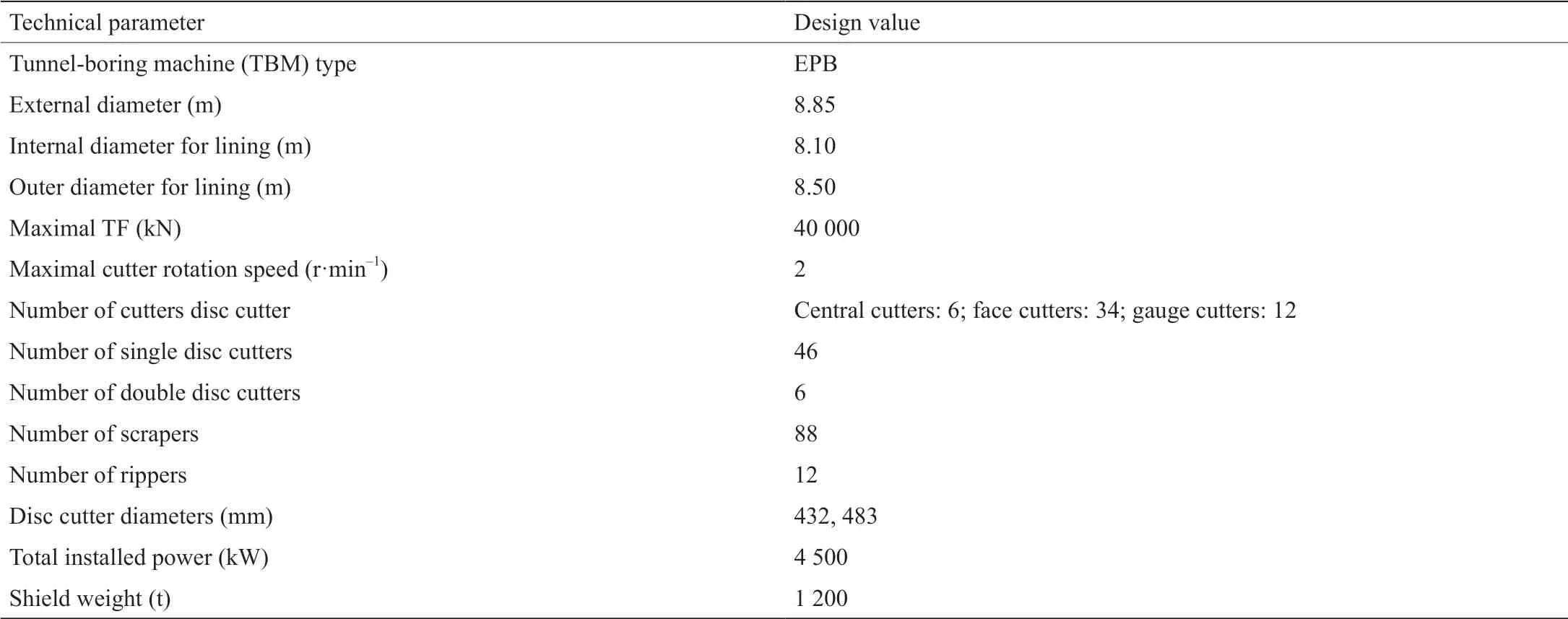
表1 本研究中EPB盾构机的主要规格

4.2. 地质条件

在开挖隧道之前，利用钻孔信息揭示地质条件。在本研究中，沿隧道每50～70 m钻几个深度约为45 m的地质孔。对岩心样品进行测试以确定土体内摩擦角和黏聚力等参数。这些参数用来区分土体特征和隧道沿线地层。土体的可塑性指数从11.90到25.10不等。此外，土体样品的稠度指数低于1。地下水位在地表以下1.63～3.63 m之间变化。根据初步地质调查结果，隧道沿线地质构造主要由回填土、粉质黏土、风化岩石和中度至高度风化花岗岩组成。表2列出了每种地层的性质。本研究的重点是盾构机在土岩复合地层中的掘进性能。对于土体软土地层，使用以下两种方法[50-53]计算了土体的不排水抗剪强度：①改进的Cam-clay模型（MCC）[53-55]；②拉德的经验公式[56]。对于MCC模型，根据以下公式确定土体的不排水剪切强度：

表2 隧道的地质描述

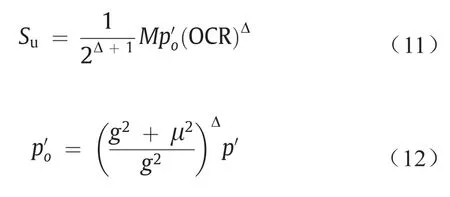
式中，Su是不排水的抗剪强度；p′是初始有效平均应力；μ=q′/p′（q′是初始偏斜应力）；OCR是过固结率；p′o是等效平均压力；g为破坏线斜率；Δ= 1 -k/λ，k和λ分别表示e-Inp′曲线和压缩线中的回弹线的斜率；e是空隙率。对于拉德的经验公式，Su估算如下：

式中，是垂直有效应力；S和k是常数，是根据Ladd的理论[56]改编的，其中，S的值为0.162～0.25，k为0.75～1.0。

对于岩层，σc值是根据以下方法计算的[57]：

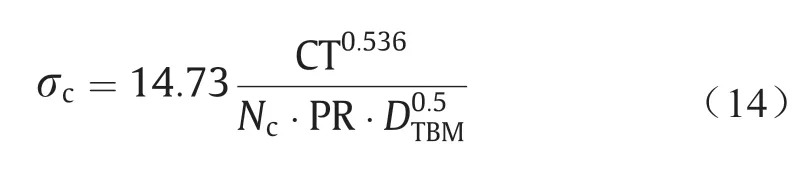
式中，σc是围岩的UCS；CT是刀盘扭矩；Nc是滚刀编号；PR是切入速率；DTBM是TBM的刀盘直径。

图4为隧道沿线地质剖面图，并介绍了岩石分类[58,59]。如图4所示，考虑了从现场提取的关键数据，如岩石质量指标（RQD）、石英含量（Qc）、节理表面状况和UCS。根据水力发电工程地质勘察规范（GB50287—2016）确定研究段的岩体分类，可用于指导开挖设计和地下工程[60]。ET-1、ET-2和ET-4区域的工程地质（ET）为软岩，如图4所示，而ET-3为硬岩[61]。

岩石的磨蚀性对于估算滚刀的使用寿命至关重要，Cerchar磨蚀指数（CAI）是一种快速、简单且经济的测定岩石磨蚀性的方法[62]。根据Cerchar的定义，变质片岩的CAI值从2.0到3.3不等。因此，地层可以定义为中等至高度磨蚀性的材料。当盾构机遇到粉质黏土时，地层为CAI值为0～1.2的轻微至中等磨蚀性材料[63]。

4.3. 滚刀磨损分析

滚刀用于切割全断面岩石地层或复合地层[64]。图5为盾构机刀盘和滚刀布置。为了确定滚刀所处位置对消耗数量的影响，根据滚刀位置对滚刀进行编号（图5）。滚刀磨损可分为两类：正常磨损和异常磨损。正常磨损是指刀圈径向均匀磨损，如图6（a）所示。异常磨损是指偏磨磨损、轴承损坏、刀圈崩坏和刀圈松动。检查滚刀时，如果滚刀刀圈发生异常损坏，应立即更换滚刀。在隧道掘进过程中异常磨损（偏磨以及崩坏或刀圈断裂）的情况下，滚刀的磨损示例如图6（b）～（d）所示。在开挖过程中，共更换112把滚刀。图7为滚刀安装位置滚刀消耗总数，大多数磨损的滚刀（超过70%）为正常磨损。根据图7（a），由于中心刀的安装半径比直径小，中心刀没有正常磨损。刀盘外边缘的滚刀消耗量增加。此外，滚刀的消耗速率表明，在标尺区域内，滚刀47～56的滚刀更换频率极高（在整个隧道掘进过程中，其更换频率比平均值高3倍）。滚刀消耗量的显著增加是因为滚刀安装角度的不同。1～46平行于隧道开挖方向且垂直于隧道工作面。而对于47～56号滚刀，刀具（弧段）的方向与开挖面之间大约呈7°～8°角。在切割过程中，在轴向推力作用下，角度越大，滚刀承受的横向力就越大。该观察结果与之前的结论一致[65,66]。正常磨损率为74.11% [图7（b）]。图8（a）展示了用于异常磨损的滚刀替换件的分布。结果显示，滚刀的消耗数量与刀盘位置的异常磨损无关，可能与复合地层的对比有关。此外，异常磨损与护罩驱动器的工作水平和岩体的破损等级有关[14,67,68]。偏磨比例为89% [图8（b）]。单把滚刀的磨损率是根据滚刀径向损失量衡量。图9为不同安装位置滚刀磨损情况的分析结果。可以推断出，面刀和边缘滚刀的磨损量随刀盘中心的距离的增长而大大增加。

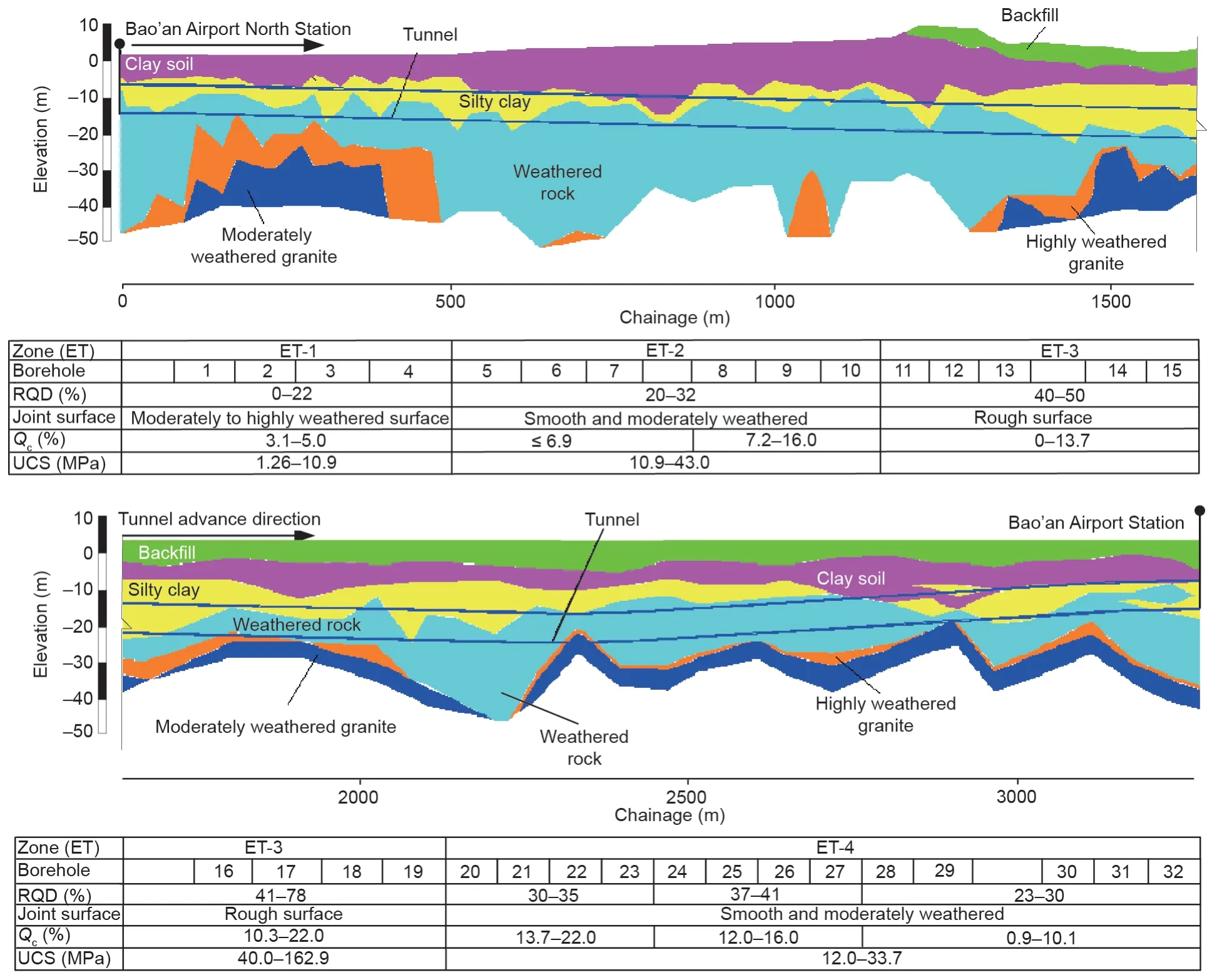
图4. 施工现场沿纵向隧道方向的地形。

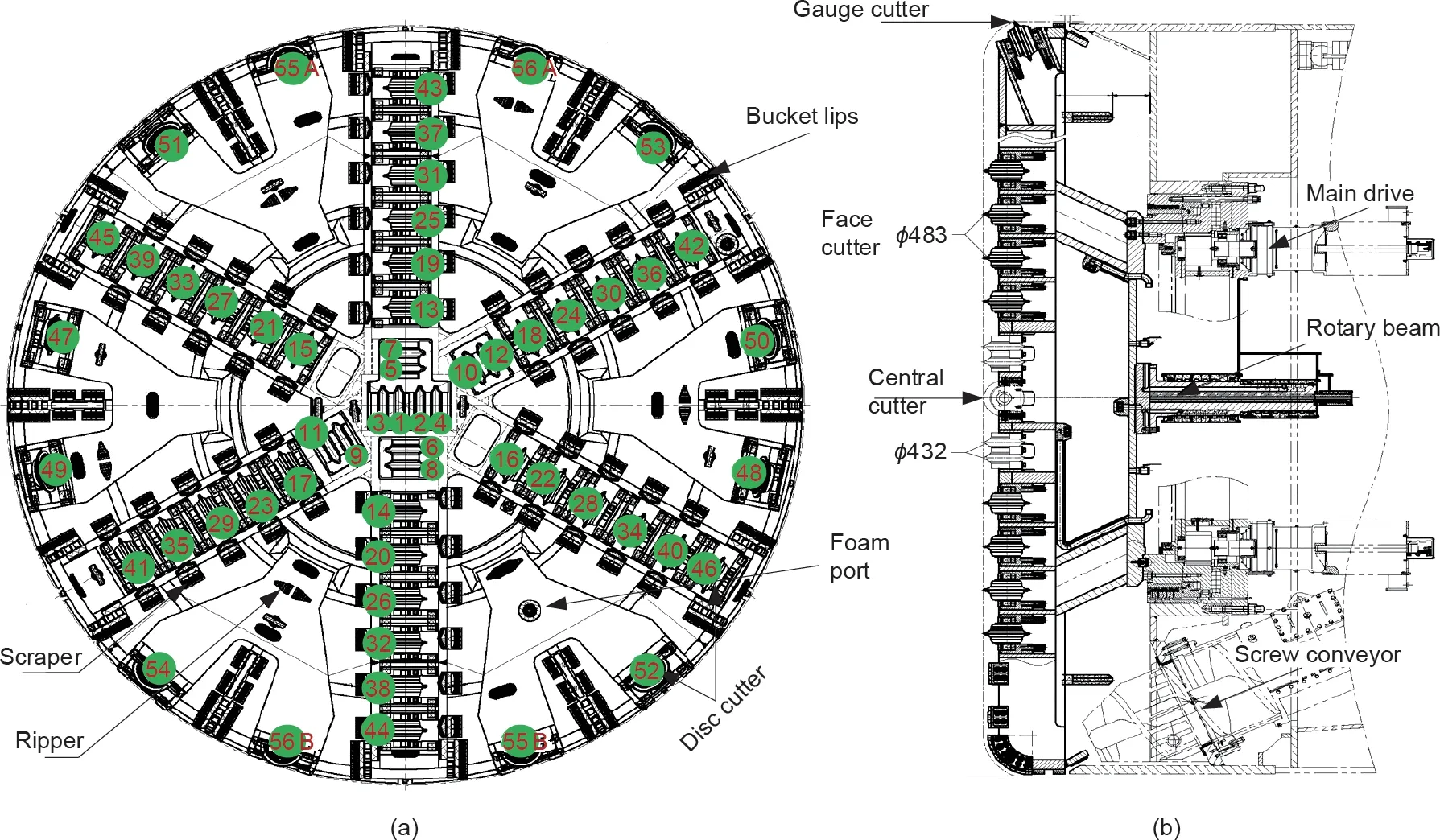
图5. EPB盾构刀盘组件。（a）带有各种挖掘工具的切刀轮；（b）机器组件。φ：刀具直径（单位：mm）；1～12号是中心滚刀；13～46是正面刀；47～56为边缘滚刀。

滚刀寿命是指滚刀需要更换之前工作的时间。Bruland [69]使用三种不同的方法表示滚刀寿命：Hm、Wm和Hf。滚刀寿命可以定义为每把滚刀的隧道开挖长度（Hm，单位为m·滚刀-1），或者通过滚刀的磨损来表示，其表示为每米挖掘土体滚动距离所改变的滚刀数量（Wm，单位为滚刀·m-1）。最后，滚刀寿命可以定义为每把滚刀的土体开挖量（Hf，单位为m3·滚刀-1）。使用下式计算：

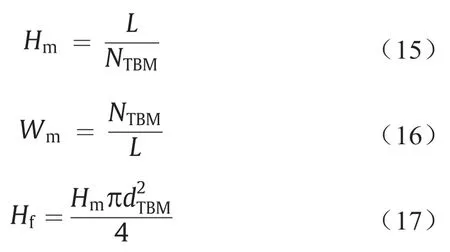
式中，NTBM、L和d分别是更换滚刀数量、开挖长度（m）和刀盘直径（m）。表3列出了本研究案例中滚刀寿命和磨损估计值。结果表明，平均滚刀寿命为29.46 m，对应于1820 m3的开挖量。在上述三个参数中，Hf是估计滚刀寿命的最合适的参数[23]。因此，Hf被用作预测滚刀寿命参数。

表3 本案例滚刀寿命和滚刀磨损计算值

图6. 滚刀磨损。（a）正常磨损；（b）偏磨磨损；（c）刀圈崩坏；（d）严重损坏。

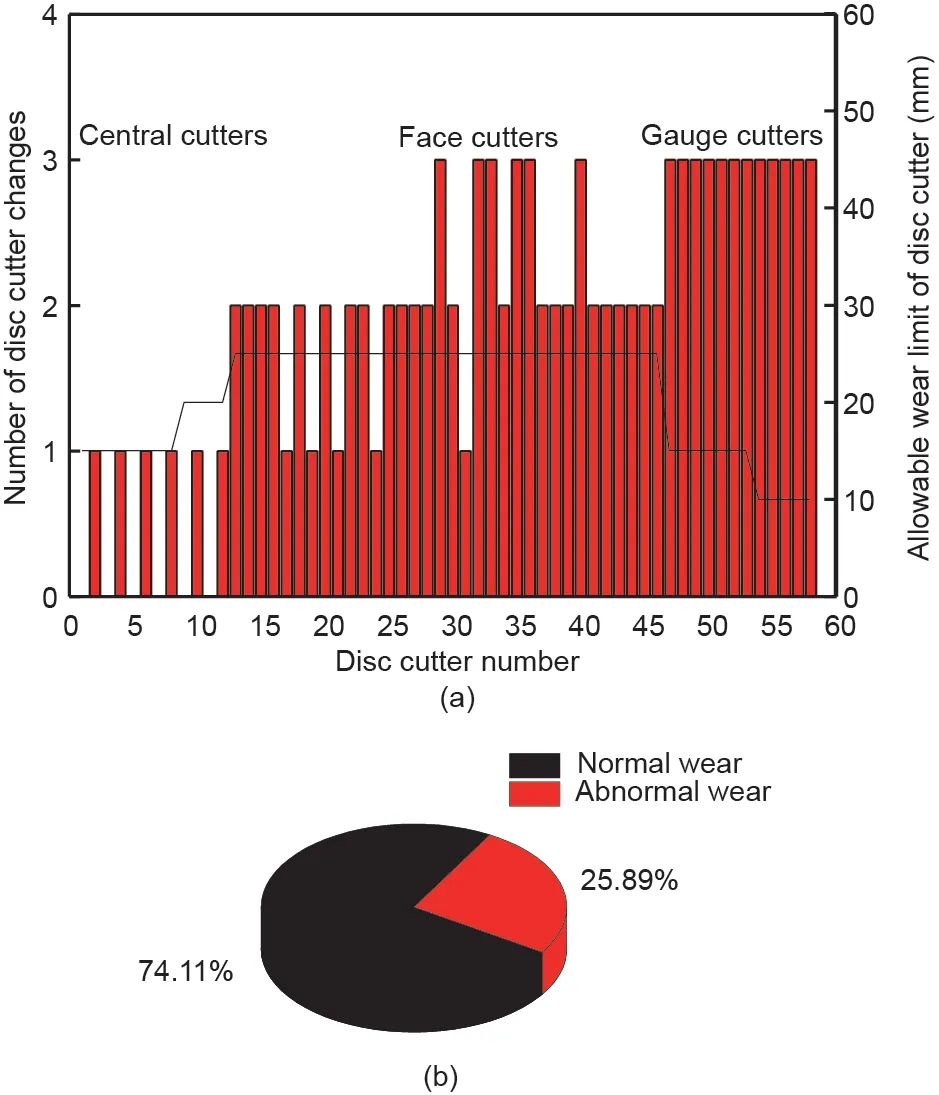
图7. 研究案例不同位置的滚刀更换（a）以及滚刀正常磨损和异常磨损的比例（b）。（a）中的实线表示磨损极限。

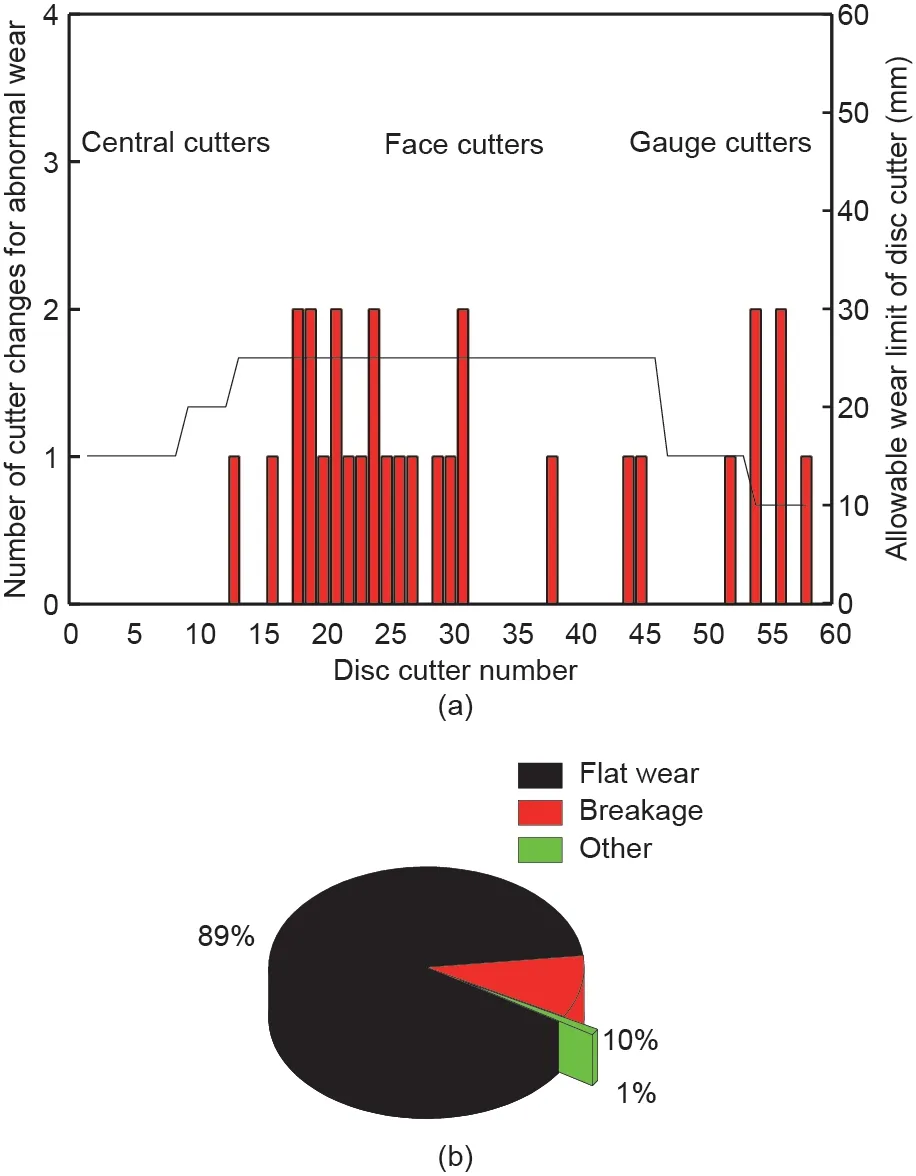
图8. 研究案例中，异常磨损滚刀消耗数量（a）以及滚刀偏磨、刀圈崩坏和其他损坏的比例（b）。（a）中的实线表示磨损极限。

4.4. 数据准备

为考虑地质条件，本研究采用钻孔和工程地质勘察报告中的数据。从提取的岩心样品中分析地质特征（4.2节）。完整的岩石特性和岩体参数用于量化地层性质。对于每个隧道分段，参数值是通过数据库中的不同测试集计算得出的[23,61,66]。然后利用这些参数的平均值来检测指定工程地质集的岩土特性。为了建立一个完整的数据库，将隧道分为具有统一地质特征的32个部分（图4）。该数据库分为两个主要类别。第一类包括地质条件，如完整的岩石特性（UCS和Qc）和岩石质量指标（RQD）。UCS的变化范围在1.26～162.9 MPa之间，Qc和RQD的最优值分别为22%和78%。第二类包含盾构操作参数，如PR、TF、GP、SP和SE。表4对输入和输出参数进行了统计分析。在本案例中，使用了由Bruland [69]提出的建议方法来估算在掘进过程中滚刀的寿命。通过收集每把滚刀更换部分的滚刀磨损和寿命来估计每把滚刀的瞬时寿命。隧道沿线滚刀寿命的变化表明，每把滚刀的寿命大多在600～2700 m3之间。此外，最大值约为最小值的4.5倍。表5列出了研究范围内滚刀寿命平均值和盾构部分操作参数。

表5 隧道沿线的开挖性能统计

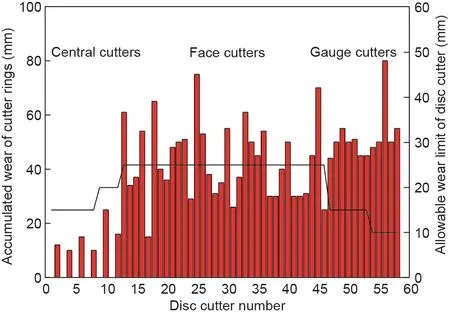
图9. 研究案例滚刀累计磨损量的直方图。（a）中的实线表示磨损极限。

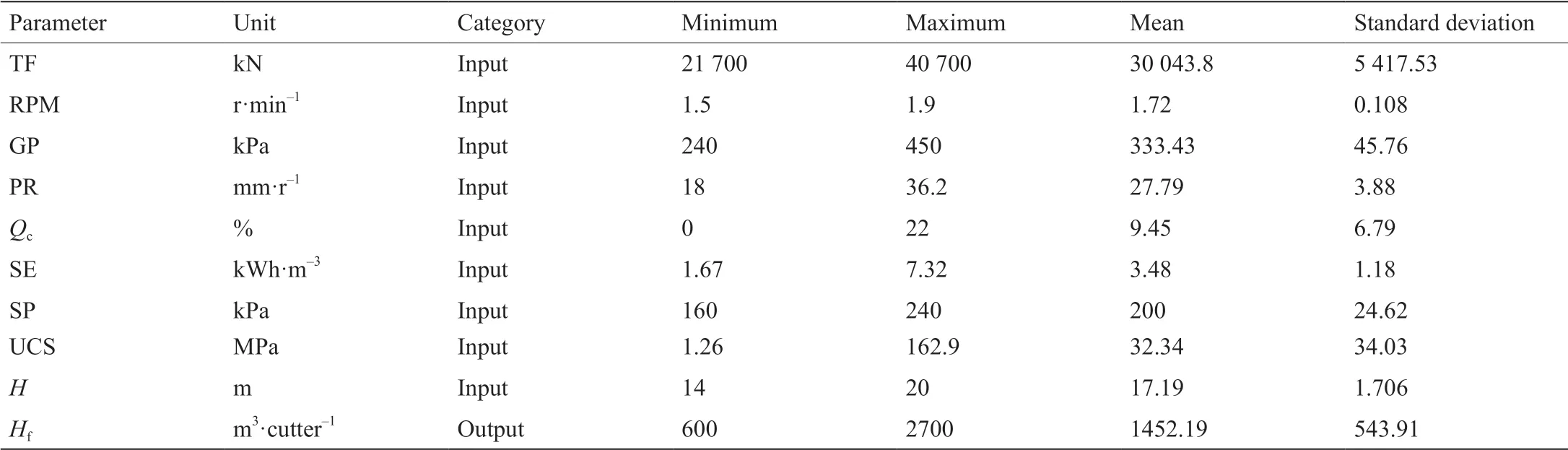
表4 本案例数据库参数统计

5. 模型开发

基于地质条件的几个经验方程用于预测岩土工程应用中的滚刀寿命[23,67]。本研究旨在发展不仅基于地质条件，同时包含盾构运行参数的经验模型，以预测滚刀的寿命。因此，利用两种统计方法（即简单回归模型和多元回归模型）建立滚刀寿命与影响因素之间的关系。

5.1. 简单回归模型

本研究中，使用刀具寿命作为目标变量分析了不同的简单回归模型。对SP、UCS、刀具转速和石英含量等不同参数对刀具寿命预测的影响进行了研究。通过线性和非线性回归模型显示滚刀寿命与某些地质和操作参数之间的相关性，如图10所示。与其他参数相比，UCS是最适合预测滚刀寿命的参数。回归系数和相关方程的结果在表6中列出。

表6 不同输入和输出参数的回归系数结果

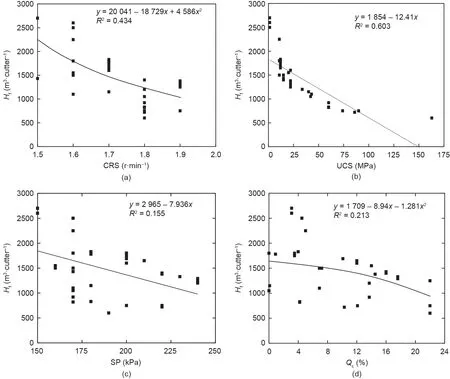
图10. 记录的滚刀寿命（Hf）与不同的操作参数和地质参数之间的关系。（a）RPM；（b）UCS；（c）SP；（d）Qc。

5.2. 非线性回归模型

刀具磨损受许多参数影响[10,14,65]。非线性多元回归模型可用于组合多个在隧道掘进过程中影响刀具寿命的参数（独立参数）。因此，采用多元回归模型来确定对现有数据进行最佳拟合的非线性解。在进行一系列拟合之后，对于PR、RPM和UCS参数[根据等式（20），最适合R2= 0.84]，获得了用于预测刀具寿命的地质参数和操作参数的最佳相关性。图11为刀具寿命的实际结果与预测结果之间的关系。表6中将提出的模型与已有模型进行了比较。显然，本文所提出的模型比已有模型能更好地预测刀具寿命。需要注意到的是，多元回归模型的结果在统计学上是有意义的。但是，为了获得更好的性能，应该开发更高级的模型。

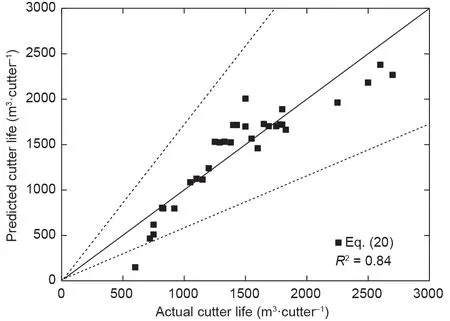
图11. 通过多元非线性回归分析比较刀具实际寿命和预测寿命。

5.3. 使用GMDH-GA评估刀具寿命

遗传算法用于优化二次函数参数，从而获得GMDH网络的最佳结构。混合GMDH-GA的实施流程如图2所示。第一步包括选择适当的输入参数。我们参考已有研究，从而确定用于预测滚刀寿命的最有效参数。预测模型的精确度依赖于经验数据的包容性和输入参数的恰当选择。如上所述，使用研究隧道分段的拓展数据范围进行模型开发。为选择最佳GMDH-GA模型结构，提出了四个模型。为确定所开发模型的预测能力，将数据随机分成两组：训练集和测试集。在本研究中使用的32 个数据集中，整个数据集（训练组）的70%用于确定方程（5）中的系数。而其他30%（测试组）用于评估训练后的模型。混合GMDH-GA的模型结构涉及几个参数（如种群大小、隐藏层数、交叉和变异的概率以及子代数量）。参数选择可能会影响模型的泛化能力。为了将GA应用于GMDH结构设计中，在300次迭代中种群数量为100，交叉概率设定为0.95，变异概率设定为0.01，其他参数没有改进。通过模型结构和模型GMDH-GA-1至GMDH-GA-4的相关方程式获得的相应多项式如表7所示。为每个模型提供了基于式（5）的这些多项式。使用具有两个变量的偏二次多项式系统。例如，在GMDH-GA-1中，Y1是根据PR和UCS估算的；Y2是根据TF和PR确定的；Y3不是独立的，而是与Y1和Y2有关。然后根据Y3和PR估算Hf。这些数学方程式及其系数可从四个不同的模型中获得，以预测盾构掘进过程中的滚刀寿命。图12显示了针对四个GMDH-GA模型开发的双隐藏GMDH层结构。选择双隐层以避免过度拟合并获得更简单的方程式。插入更多隐藏层大大增加了已建立模型的复杂性，但没有取得实质性的改进。

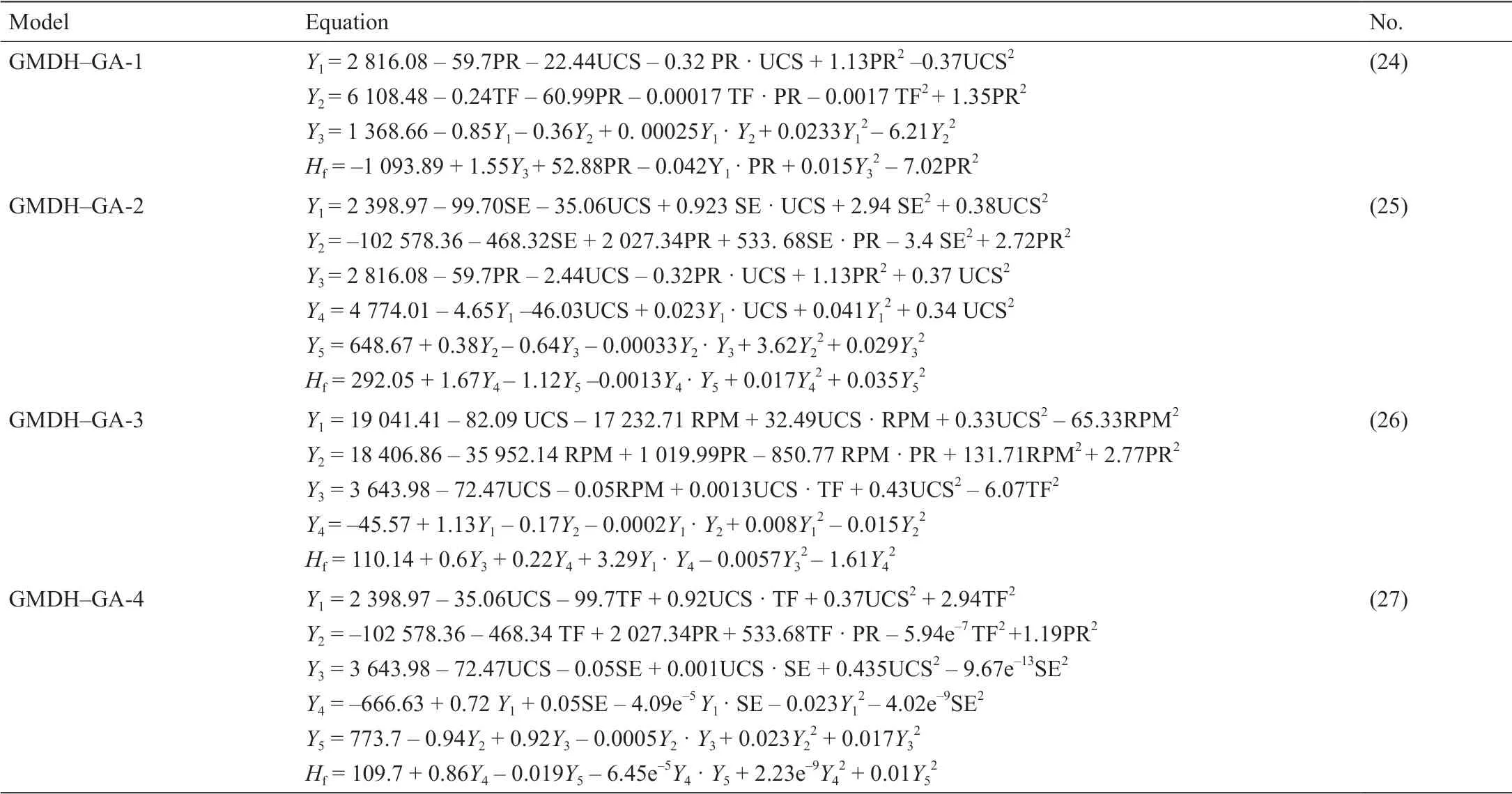
表7 神经元方程式中使用的参数和系数

应用均方根误差（RMSE）和相关系数（R2）评估GMDH-GA的预测结果与现场数据之间的偏差：

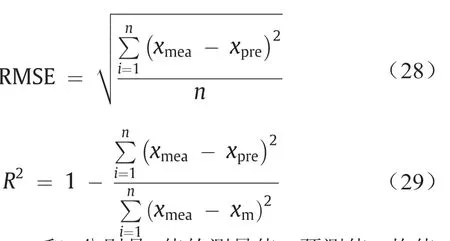
式中，xmea、xpre、xm和n分别是x值的测量值、预测值、均值以及数据的总数。

图13为刀具实际寿命和预测寿命间的关系。根据图 13，来自四个GMDH-GA模型的刀具预测寿命对于训练和测试数据集均显示出较好的相关性。此外，滚刀寿命预测值在对应于±20%的曲线上，这表明在隧道掘进过程中，混合模型在刀具寿命预测中具有很高的准确性。预测Hf的最佳二次多项式模型由UCS、PR、TF和RPM组成，并在模型GMDH-GA-3中给出，如表8所示。该模型误差相比于其他模型低得多。通过最小化RMSE和最大化R2可以实现更好的精度。此外，将最佳混合GMDH-GA模型与从多元非线性回归[方程（20）]获得的方程式进行比较，以评估其准确性。结果显示该混合模型可以通过地质参数和操作参数有效地预测刀具寿命，即与R2= 0.84和RMSE = 218的经验方程相比，相关系数R2= 0.967和RMSE = 97.22。

表8 进化GMDH-GA模型的统计结果

图12. 用于预测Hf的双隐藏GMDH层的演化结构。

5.4. 敏感性分析

对提出的模型进行敏感性分析，以确定每个输入参数对模型输出的影响。通过以恒定速率改变每个输入参数并保持其他输入变量不变，对GMDH结构的双重隐藏层进行分析。利用余弦振幅模型进行分析[49]：

5.5. 讨论

根据上述经验模型，滚刀的使用寿命基本上取决于地质参数和操作参数。为获得更准确的结果，将遗传算法应用于GMDH模型以优化二次函数参数，从而提高模型准确性。四个参数（UCS、PR、TF和RPM）与刀具磨损密切相关，因此被用作预测滚刀寿命的因素。GMDH-GA-3模型的结果证实，使用这四个参数有助于准确地预测滚刀的使用寿命（图13）。为了评估每个输入参数对模型输出的影响，进行了敏感性分析。利用本研究的结果，现场施工人员可以对滚刀寿命的预测有更深入的了解，并可以在不同的预测模型之间做出合理的选择。值得注意的是，UCS对滚刀的寿命有明显的影响。可用来分析滚刀的使用寿命，以评估和推测地质条件的变化。考虑到盾构操作参数的重要性，本研究的方法对于因素导向方法的创建很有必要。此外，混合模型GMDH-GA-3中使用的参数反映了现场条件，并且随刀具磨损的变化而不同。因此，该模型可以及时可靠地预测滚刀的寿命。

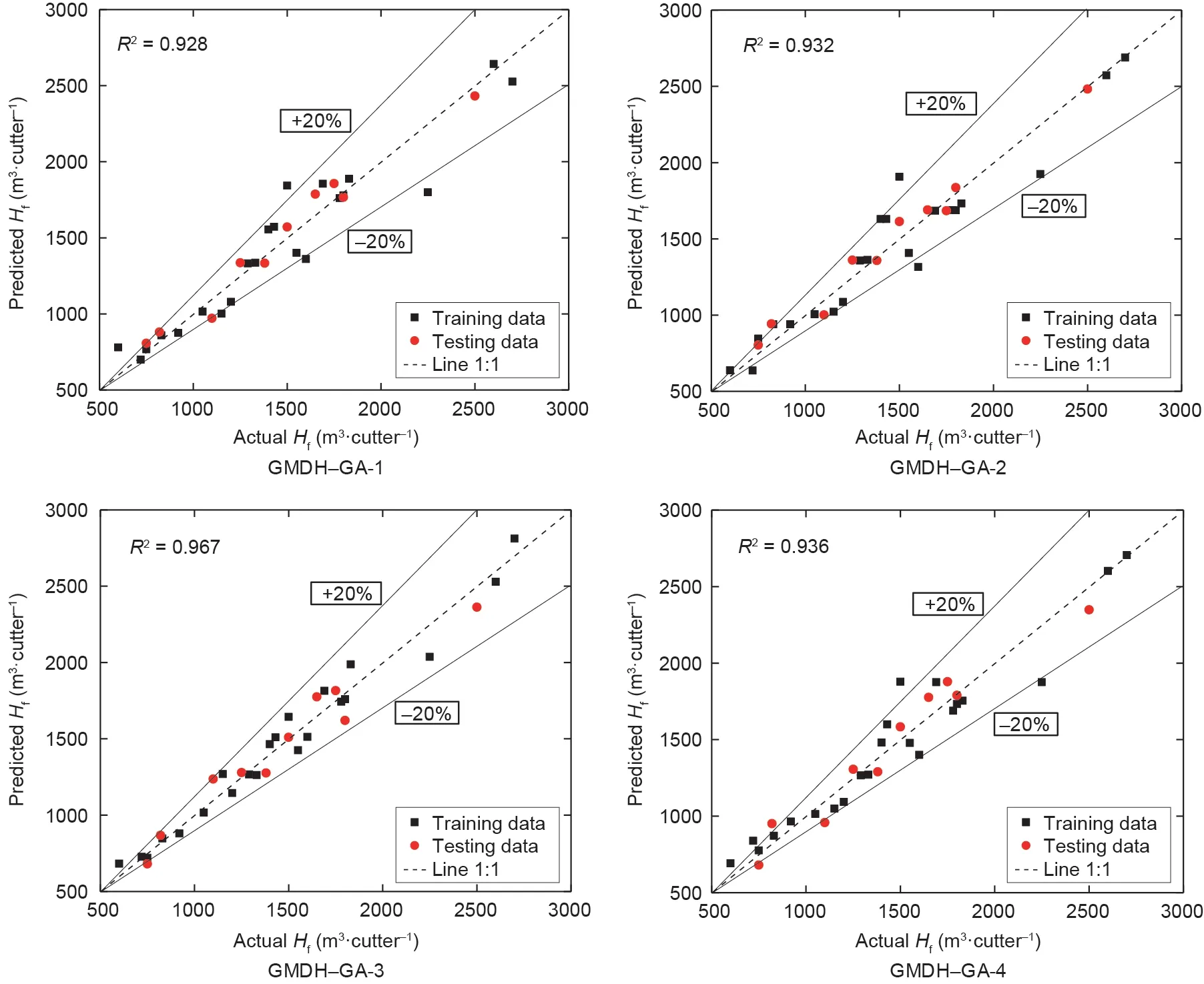
图13. GMDH-GA（1）～（4）模型实际Hf和预测Hf比较。

最后，必须指出的是，盾构掘进通常在岩石-土体复合地层中进行，因此受益于刀盘及刀盘设计和制造技术的改进。本文研究的EPB盾构机已用于许多隧道工程中，尤其是在中国，例如，在珠江三角洲的穗莞深（广州—东莞—深圳）城际铁路[8]、广州南站城际铁路项目、湖南长沙的铁路隧道项目[70,71]以及广州和佛山之间的城际隧道项目（建设中）。但是，对于具有不同刀盘的情况，可能需要作出调整。

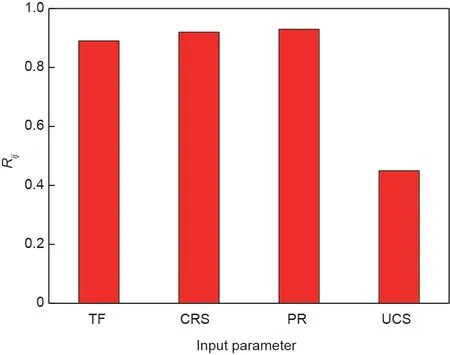
图14. 每个输入参数对双重隐藏层模型的输出的影响。

6. 结论

本研究提出了一种基于人工智能的岩石-土体复合地层盾构掘进过程中滚刀寿命预测方法。为了提高模型准确性，对数据集进行整理并进行统计分析，以预测滚刀寿命并提高盾构机掘进性能。所提出的模型不仅包含地质参数，还包括盾构运行参数。本文结论 如下：

（1）结果表明，正常磨损会严重影响滚刀的使用寿命，并且滚刀的累积磨损量会随着离刀盘中心距离的增大而增加。

（2）所提出的经验模型可以快速评估施工参数和结果验证，从而可以将刀具寿命预测精度控制在可接受范围内（R2= 0.84）。

（3）GMDH-GA模型可以准确预测滚刀寿命，与经验模型相比，预测准确性显著提高。为评估输入参数对模型输出的影响，进行了敏感性分析。结果表明，使用双隐藏GMDH层所预测的PR会显著影响滚刀的使用寿命。

（4）在模型应用中，提出的GMDH-GA模型可以使用盾构操作参数（TF、PR、RPM）和地质参数（UCS）作为输入，以预测隧道掘进过程中的滚刀寿命。所提出的模型是通用的，可用于分析其他相似地质和环境条件隧道施工。最终，所提出的模型有望提供有效的建议，从而帮助现场施工人员预测滚刀的使用寿命。它可以作为在计划和施工阶段均可使用的滚刀寿命智能预测方法。

致谢

本研究工作由广东省“珠江人才计划”引进科技创新类领军人才项目（2019CX01G338）、汕头大学引进教师启动基金项目（NTF19024-2019）资助。

Compliance with ethics guidelines

Khalid Elbaz, Shui-Long Shen, Annan Zhou, Zhen-Yu Yin, and Hai-Min Lyu declare that they have no conflict of interest or financial conflicts to disclose.