基于可控参数的前馈神经网络出水总氮预测模型研究

赵子豪，王子昊，袁家洛，马骏，何哲灵，徐一兰，沈晓佳，朱亮,b,c,*

a Institution of Environment Pollution Control and Treatment, Department of Environmental Engineering, Zhejiang University, Hangzhou 310058, China

b Zhejiang Province Key Laboratory for Water Pollution Control and Environmental Safety, Hangzhou 310058, China

c Zhejiang Provincial Engineering Laboratory of Water Pollution Control, Hangzhou 310058, China

d Haining Water Investment Group Co., Ltd, Haining 314400, China

e Haining Capital Water Co., Ltd, Haining 31440, China

1. 引言

近年来我国工业化城镇化进程不断加快，污水排放量攀升至每年669.6亿t以上[1]。为削弱污水排放所带来的环境不利影响，我国陆续采取新建或改扩建污水处理厂、修订污水排放标准等一系列措施。截至2018年年底，我国共有5370座污水处理厂处于正常运行状态，日处理能力达2.01×108m3，总用电量达1.972×1010kW·h-1[2]。据调查，目前我国多数城镇污水处理厂存在出水水质难以稳定达标、运行药耗能耗偏高、自动化控制程度较低等问题，亟需科技支撑予以解决。

序批式活性污泥工艺（SBR）因其工艺简便、操作方式灵活、抗负荷性能优异等特点，已成为我国应用较为广泛的污水处理工艺之一[3]。然而，SBR工艺对系统操控自动化水平要求较高，极易产生出水水质指标（尤其是总氮）波动大、运行能耗过高等问题[4]。而在SBR工艺中，脱氮是十分复杂的，包括好氧条件下的硝化反应及缺氧条件下的反硝化反应[5]。已有研究表明，溶解氧（DO）控制是实现污水处理系统总氮（TN）有效去除的重要因素，充足的DO可保证有机物降解及硝化反应顺利进行，但过量的DO则会导致污水处理能耗过高、反硝化效率降低、污泥性能恶化[6]。同时，根据现有工程运行情况来看，污水处理系统DO难以实现精准控制，主要与DO监测设备准确度低、响应慢，传统拟合模型和控制理论相对落后有关[7,8]。在大多数污水处理厂，操作人员往往根据经验调整表面气速、缺氧段时长等控制参数，从而实现体系DO浓度的相应调控，这样的操作方式也比DO精准控制更为简便。

鉴于污水生物处理系统参数众多、过程复杂，传统的生化模型难以拟合其高维的非线性数据，进而难以应用到实际污水生物处理工艺中[9,10]。而人工神经网络（ANN）作为一种自学习算法模型，理论上能够拟合任意非线性函数，因而其可作为预测污水生物处理这种复杂非线性系统的有效工具[11-13]。从神经元拓扑结构来看，ANN可分为反馈神经网络和前馈神经网络（FFNN），其中，FFNN模型理论上可以任意精度逼近任意连续函数，具有较强的分类和模式识别能力[14-19]。为进一步提高FFNN的预测效率与能力，研究者陆续提出了Levenberg-Marquardt (L-M)、贝叶斯正则化（BR）、量化共轭梯度（SCG）、动量和Nesterov加速梯度等多种优化算法，显著提高FFNN模型的预测能力和效率[20-22]。

本文以序批式活性污泥工艺为研究平台，构建了一种基于可控参数的前馈神经网络出水总氮预测模型。与已有预测模型相比，本模型具备以下两个特点：①采用可控参数（表面气速与缺氧段时长）代替溶解氧作为模型主要输入参数，明显提高模型可用可控性；②采用算法优化的FFNN构建模型，显著提高模型预测精准度。本文的研究目的主要在于评估优化后FFNN模型的SBR工艺出水TN预测准确性，明确合理地运行参数控制策略以实现污水处理厂污染物高效去除与系统节能降耗。

2. 材料与方法

2.1. SBR工艺长期仿真实验

本研究设置两组平行运行的SBR反应器（R1、R2），开展持续两个月的长期仿真实验。反应器活性污泥取自浙江省某城镇污水处理厂，进水模拟该污水处理厂的实际进水。反应器结构及模拟废水组成如附录A中的图S1、表S1所示。

参考该污水处理厂SBR工艺的实际运行模式，每组反应器的运行周期设为4 h，包括进水（5 min）、缺氧与曝气期（210 min）、沉降期（5 min）、出水（5 min）、闲置（15 min），体积交换比设为50%。配置进水时，随机控制主要水质指标浓度为预设值的75%～125%，模拟实际进水水质波动情况。分别设表面气速与缺氧段时长作为控制变量，其设计值如表1所示。每个周期分别对进出水进行取样，采用标准方法分析进出水的总氮（TN）、氨氮（NH4+-N）、化学需氧量（COD）和总磷（TP）浓度[23]。经两个月的仿真运行后，从控制变量的16种组合中获取124组数据供后续建模使用。

表1 SBR工艺控制变量的设计值

为拟合更复杂的运行状况，本研究引入缺氧段后进水占比并设置范围更广的控制变量后开展扩展实验，共收集91组数据，其设计值如表2所示。同时为仿真实际运行中的极端情况，本研究分别设置表面气速为3.6 cm·s-1、4.8 cm·s-1，缺氧段时长为0、150 min，并从其组合中收集11组数据。

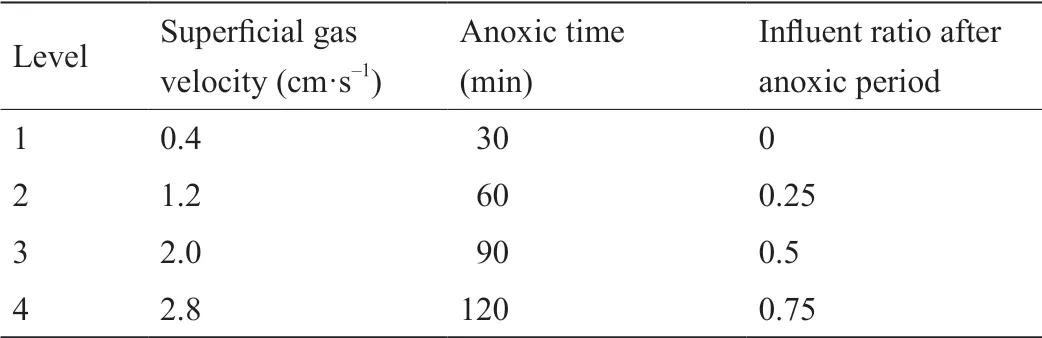
表2 扩展实验中引入缺氧段后控制变量和进水比的设计值

2.2. FFNN建模

基础FFNN模型及其优化算法均在Matlab R2016a中搭建并运行。建模前，将长期仿真得到的数据集归一化至0.001～0.999，以消除数据间不同量纲的影响。FFNN模型在构建过程中根据模型预测值与实际值的误差不断优化权值网络[式（1）] [24]，其网络结构包括输入层、隐藏层及输出层三部分，其中进水水质（COD、TN、NH4+-N、TP）与运行参数（表面气速、缺氧段时长）6个变量作为模型的输入变量，出水TN则作为模型的输出变量，建模示意图如图1所示。由于实验数据维度较低，设置FFNN模型隐藏层数为1层以缩短运算时长，提高效率，同时防止过拟合现象发生。而模型隐藏层最佳结点数则参考经验方程进行计算[式（2）]。

式中，a为输出变量；W为权值矩阵；d为输入变量；b为偏置。

式中，h为隐藏层结点数；i为输入层结点数；o为输出层结点数；c为常数，一般选在1～10之间。

2.3. FFNN模型优化

基础FFNN模型参照传统的反向传播（BP）神经网络进行构建。在训练阶段，BP神经网络根据预测值与实际值误差的反向传播不断调整其权重网络，使误差最小化。梯度下降法则是模型调整权重的最常用算法，即沿梯度下降的方向调整权重并最小化误差[25]。但在实际训练过程中，梯度下降法在迭代求解时容易最小化误差至局部极小值而不是全局最小值，因而降低了模型学习效率与预测准确度[26]。为提高模型的学习效率与预测准确度，本研究采用三种优化算法（L-M、BR以及SCG）对FFNN模型进行优化，对比三种优化算法得到最适合SBR工艺的优化FFNN模型。同时，为进一步提高模型的泛化能力，采用更复杂的数据集（即包括扩展实验数据集）训练模型，缺氧段后进水比将代替进水TP作为模型的输入参数。

2.3.1. L-M算法

L-M算法结合高斯-牛顿算法以及梯度下降法的优点，能有效避免局部最小值并提高全局最小值的收敛速度，其算法如下。

若将BP神经网络中各层间的权值用向量W表示，其误差平方和（E）为

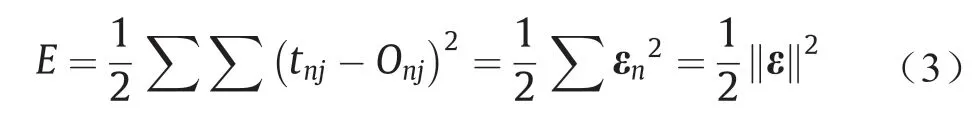
式中，n为样本编号；tnj为样本n在输出层j结点的期望输出；Onj为该结点实际输出；ε是以εn为元素的向量。

在式（4）中，k代表迭代次数（即权重更新的次数）。在计算Wk+1的过程中，如果移动量Wk+1-Wk很小，则可将ε展开成一阶泰勒级数：

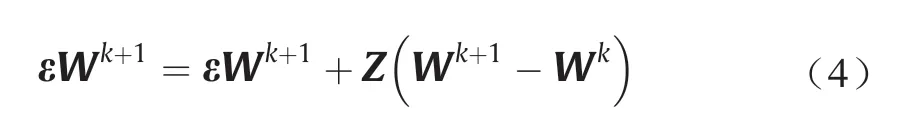
式中，Z是ε的雅可比矩阵，Z的元素为

由此，误差函数可改为

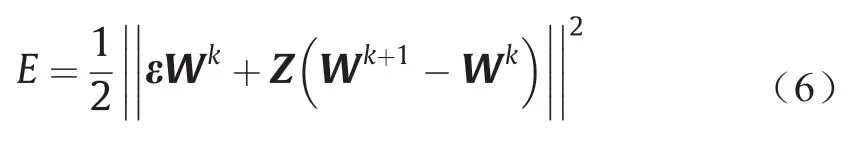
要使误差函数最小，可对Wk+1进行求导，得到如下高斯-牛顿迭代公式：

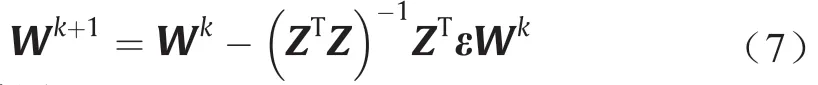
式中，T代表转置。

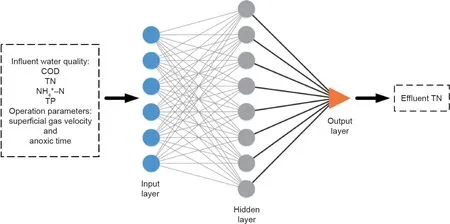
图1. 出水总氮预测FFNN模型的网络结构。

为克服高斯-牛顿法中经常出现的雅可比矩阵奇异现象，把误差函数改写为

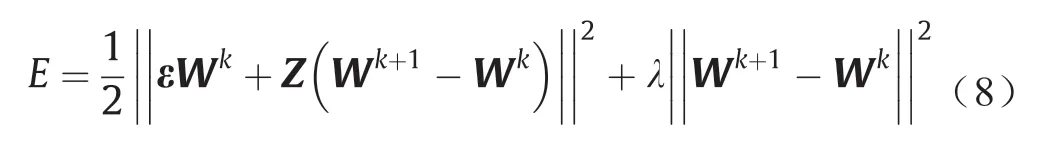
式中，λ为阻尼系数。

此时对E求导，便可得到基于高斯-牛顿法的L-M迭代公式：

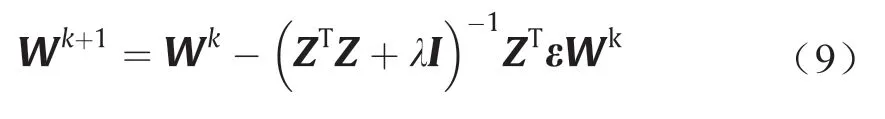
式中，I为单位矩阵，为迭代变量。在迭代过程中搜索方向与训练步长受λ变化影响。在计算初始阶段λ可取较大值，这时ZTZ与λI相比是可以忽略的，于是上式可写为

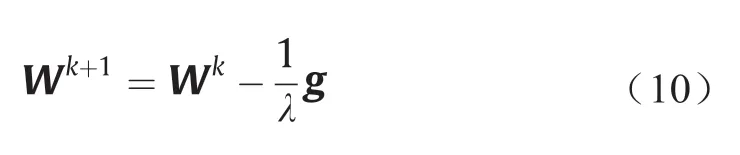
式中，g为梯度。若令λ趋于零，则该表达式可变为高斯-牛顿迭代公式。

2.3.2. BR算法

BR算法指贝叶斯方法正则化神经网络。所谓正则化是指训练阶段为神经网络添加惩罚项来限制网络的复杂度。经正则化后，神经网络可有效避免过拟合现象的发生，提高模型的泛化能力。通常来讲，神经网络的性能函数可表示为

经过添加惩罚项EW后，其性能函数转变为

α和β的相对大小决定了惩罚项所占比例。如果α＜＜β，则近似于无正则化条件，侧重于最小化训练误差，但可能过拟合。若α＞＞β，则侧重于限制网络权值规模，但可能降低模型预测性能。因此，如何确定α和β值是非常重要的。在贝叶斯分析的框架下，MK推导出[27]：

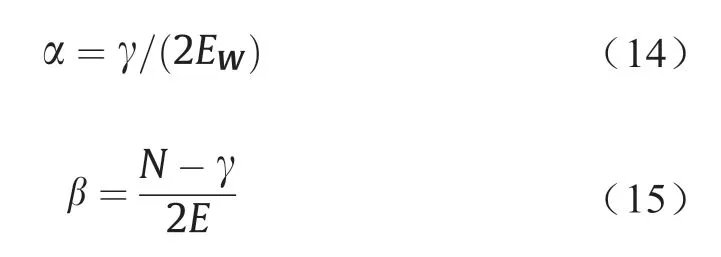
式中，γ=N-2αtr(H)-1表示有效权值数，N为样本总数；H是F的海森矩阵：

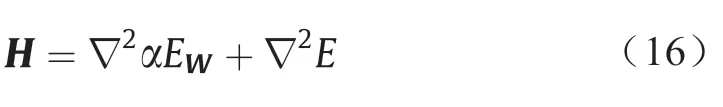
但海森矩阵计算量很大，Foresee和Hagan用高斯-牛顿法近似计算海森矩阵，大大降低了计算量[28]：

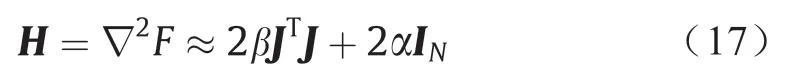
式中，J是训练误差的雅可比矩阵。

2.3.3. SCG算法

SCG算法是一种标准BP神经网络的改进算法。在神经网络训练中，传统的梯度下降法只能沿负梯度的方向进行收敛，并不一定会正确收敛到全局极小点。共轭梯度法则可将负梯度方向与上一次搜索方向结合起来，计算出新的搜索方向。但该算法每次迭代时都需要重新确定搜索方向，进而导致其计算量巨大。Moller [29]提出的SCG算法将模型置信区间法与共轭梯度法结合起来，成功解决了上述问题。SCG算法的权值调整方法转变为

式中，wk为Wk中一点；pk为第k次迭代时的搜索方向；θk为第k次迭代时的搜索步长。

式中，gk为第k次迭代时的梯度；Hk为第k次迭代时的海森矩阵。

令sk=Hkpk,δk=pkTsk,uk= －gkTpk，则有θk=uk /δk。同时为了保证δk＞ 0，令δk=pkTsk+λk|pk|2。

最后可得到步长θk：

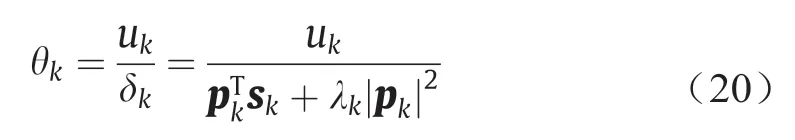
2.4. 模型性能评价指标

本研究采用相关系数（R）[式（21）]评估各个模型的预测能力，采用均方误差（MSE）[式（22）]评估训练过程中各模型的拟合能力。R与MSE均在Matlab R2016a中计算完成。

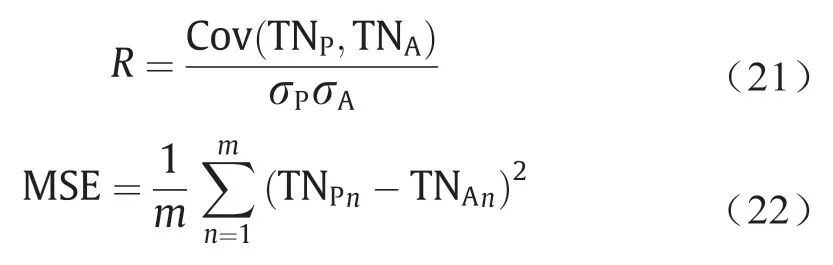
式中，Cov (TNP,TNA)代表出水TN预测值与实际值的协方差；σp、σA分别为出水TN预测值与实际值的标准差；m为数据集样本量；Pi为第i个样本的出水TN预测值；Ai为第i个样本的出水TN实际值。

3. 结果与讨论

3.1. 采用运行参数作为主要输入变量构建FFNN模型的可行性

建模时首先确定神经网络隐藏层结点数。在其他参数不变的情况下，根据式（2）计算可得，隐藏层结点数q应取在3～12之间。训练完成后，不同结点数模型的均方误差如图2所示。对比发现，神经网络隐藏层结点数为8时，MSE最小，因而确定基础FFNN模型的网络结构为6-8-1。

为训练和评估基础FFNN模型，本研究将SBR工艺长期仿真实验中所收集的数据随机分为训练集（104组）和测试集（20组）。图3为模型对整体数据集的拟合程度，可见其左侧（训练集）的预测值与实际值较为接近（R= 0.91973），表明采用可控参数（如表面气速、缺氧段时长）代替DO作为输入构建模型是可行的。但右侧测试集中预测值与实际值相差甚远（R= 0.5057），说明该模型仍存在过拟合或陷于局部极小值等降低模型预测性能的问题。针对这些问题，本研究采用L-M、BR和SCG三种算法对神经网络模型进行优化。同时采用更复杂的数据集对模型进行训练，并针对不同的算法建立更合理的训练模式，找出最适合模型的算法。

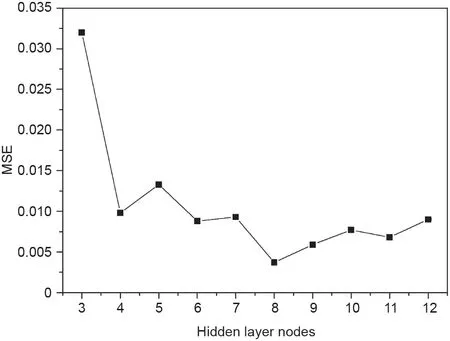
图2. 具有不同隐藏层结点数的FFNN模型的均方误差。

3.2. 采用L-M算法优化FFNN模型

将数据集随机分为训练集（80%）和验证集（20%）。通过尝试法优选后，设置隐藏层结点数为30，最小失败次数为100，隐藏层与输出层间传递函数为tansig。训练113步后，因验证集失败次数超过设定值，停止训练，共用时1.0 s，其拟合结果如图4所示。由图可知，该模型的MSE为0.00200，在训练集、验证集与全集中的R值分别为：0.93603、0.92316、0.93392，表明该模型对出水TN的预测性能良好。L-M算法优化后的模型比之前的基础FFNN模型具有更高的R值和更快的收敛速度，不仅有效避免了局部最小值，而且提高了收敛到全局最优的速度。

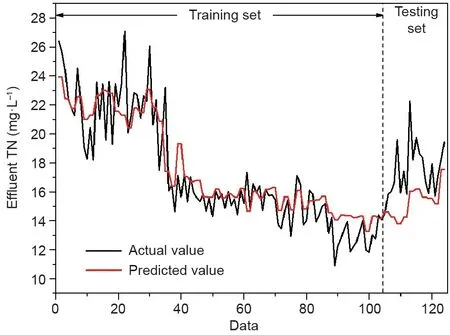
图3. FFNN模型预测值与实际值的比较。

3.3. 采用BR算法优化FFNN模型

BR算法不需要验证集，因此将数据随机分为训练集（80%）与测试集（20%）。模型调试过程发现，当隐藏层结点数小于20 时，预测值与实际测量值之间的相关系数低于 0.6，表明模型拟合程度较差；随着隐藏层结点数逐渐增加至30，R值逐渐升高，结点数超过30后R值升高不明显，但训练时间大幅增长，故选取隐藏层结点数为30。选取Tansig作为传递函数，设置训练步数上限为1000后，该模型训练用时19 s。如图5所示，训练集的R值为0.90232，而测试集的R值为0.83000，说明该模型的预测性能优于基础模型，但弱于L-M算法优化的模型。BR算法通过限制网络的复杂性提高了模型性能，使得R值比基础模型更高。尽管如此，正规化可能会使得模型丢失一些输入输出之间的关系，特别是在模型结构复杂性中等的情况下。

3.4. 采用SCG算法优化FFNN模型

与L-M算法相似，数据集被划分为训练集（80%）和验证集（20%）。隐层结点数选为30，以保证与三种算法模型结构一致。选择Tansig作为隐藏层与输出层之间的传递函数，最小失败次数设为100。因失败次数超过预设值，该模型在训练156步后停止，其训练时间接近于零。如图6所示，其训练集的R值为0.916，验证集的R值为0.962。验证集R值高于其训练集R值表明该模型不存在过拟合现象且具有良好的预测性能。

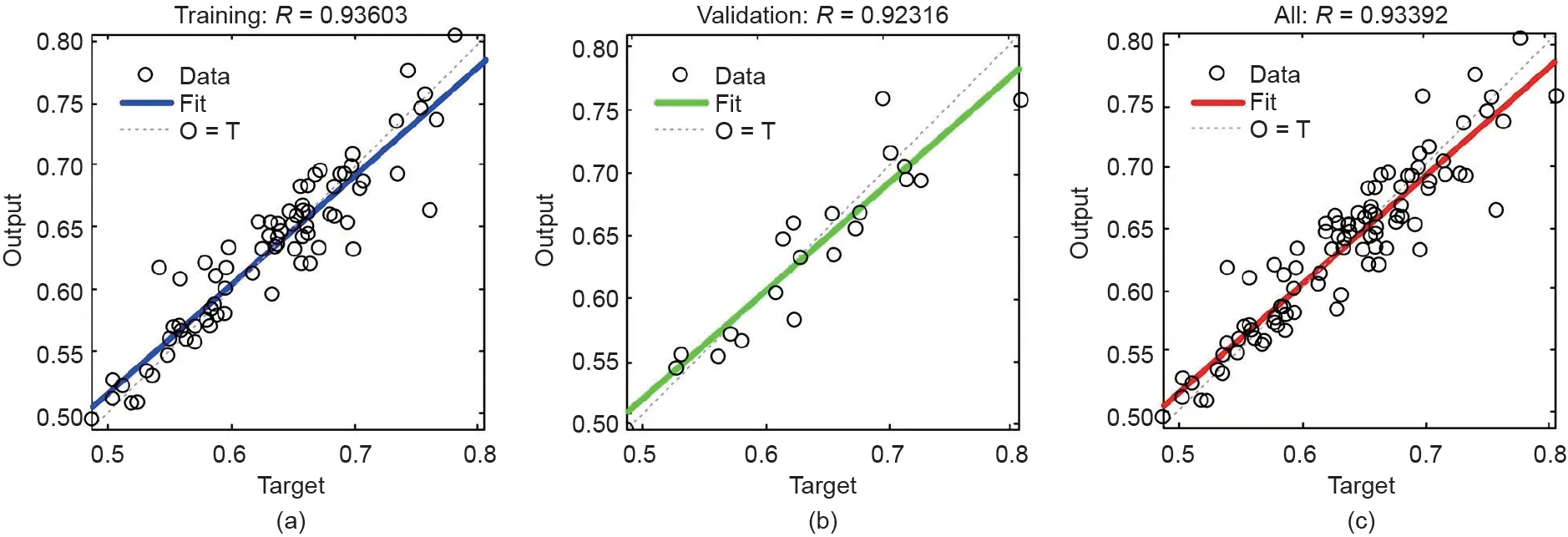
图4. 基于L-M算法的FFNN模型仿真结果。（a）训练集（输出≈0.88×目标+0.075）；（b）验证集（输出≈0.88×目标+0.074）；（c）全集（输出≈0.88×目标+0.077）。“Fit”一行表示目标和输出之间的关系；“O=T”一行表示目标等于输出。

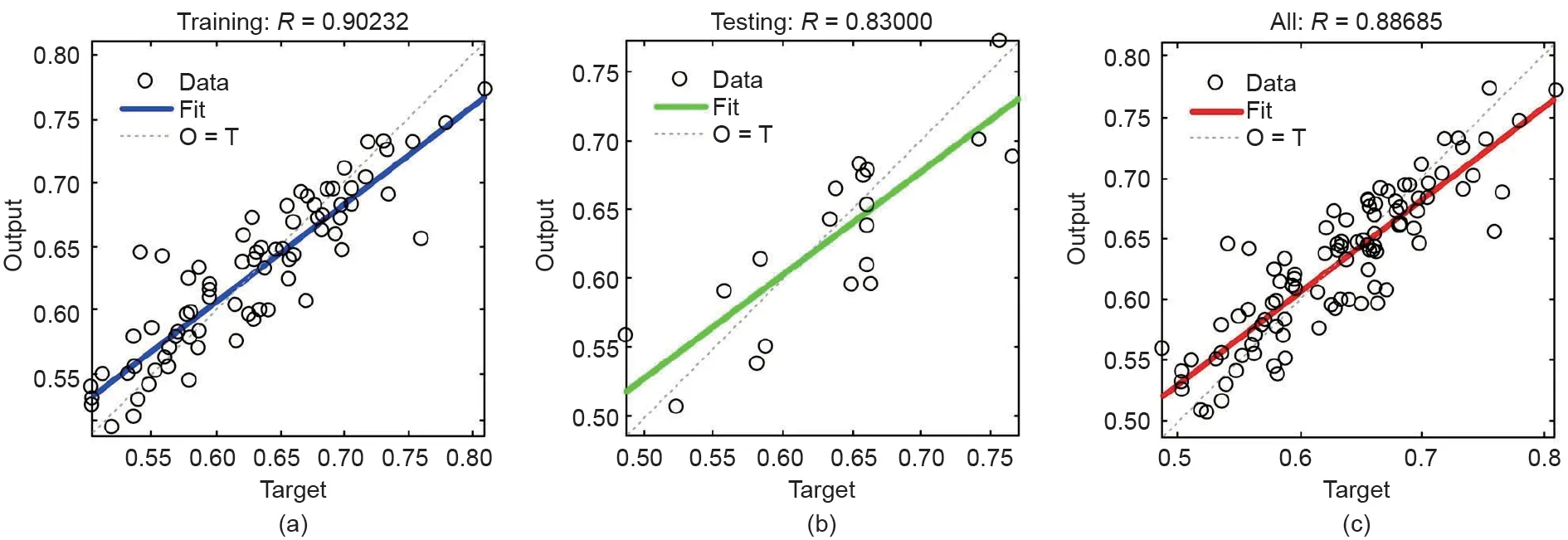
图5. 基于BR算法的FFNN模型仿真结果。（a）训练集（输出≈0.76×目标+0.15）；（b）测试集（输出≈0.75×目标+0.15）；（c）全集（输出≈0.76×目标+0.15）。

3.5. 三种优化算法的比较

基于不同优化算法的FFNN模型训练参数如表3所示。由表可知，训练期间三种算法优化后的FFNN模型的MSE均较低（＜ 0.001），表明其拟合能力均优于基础模型（MSE = 0.0037）。其中，SCG算法的训练时间最短。

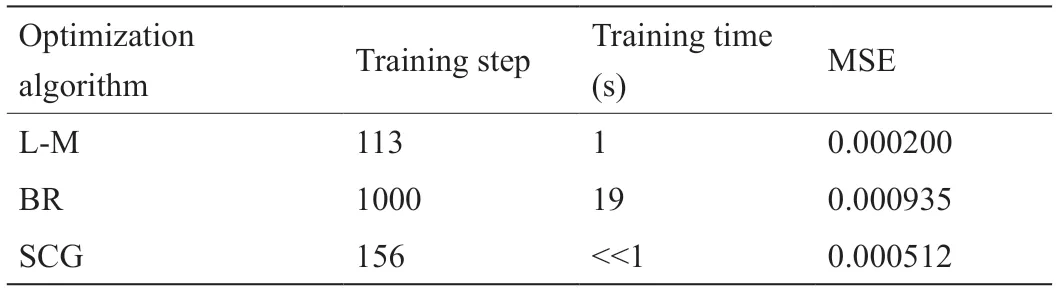
表3 基于不同优化算法的FFNN模型训练参数

基于各优化算法所构建的FFNN模型R值如表4所示。训练期间三种模型的R值分别为0.936、0.902和0.917，说明模型训练集的输入（进水水质和运行参数）和输出（出水TN）相关性较强。在预测阶段，所有FFNN模型的R值均高于基础模型，表明优化算法大大提高了FFNN神经网络模型对出水总氮的预测性能。其中，基于SCG算法的模型R值最高并高于其训练集的R值且训练时间最短，表明SCG算法能够使模型获得最快的计算速度和出色的预测能力，是最佳的优化算法。

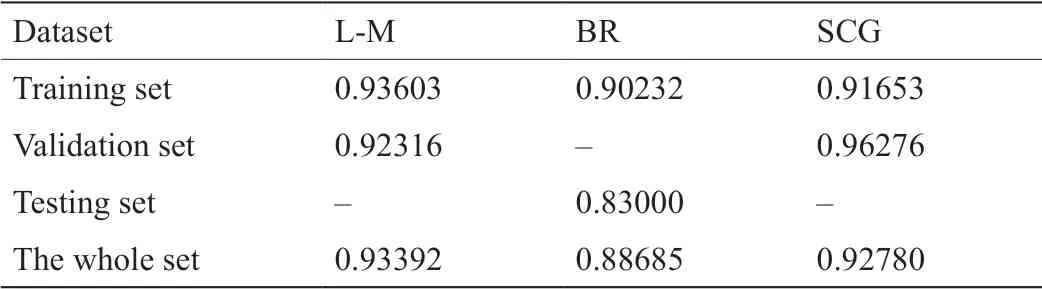
表4 基于各优化算法所构建的FFNN模型R值

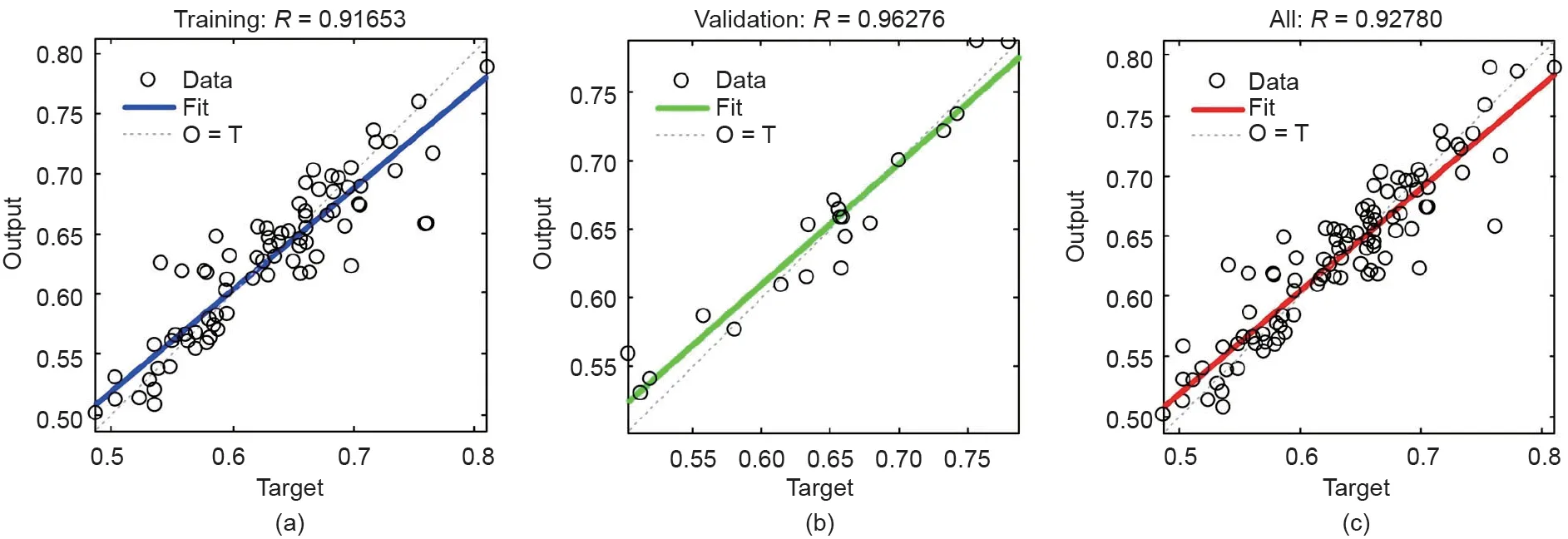
图6. 基于SCG算法的FFNN模型训练结果。（a）训练集（输出≈0.84×目标+0.1）；（b）验证集（输出≈0.88×目标+0.079）；（c）全集（输出≈0.85×目标+0.092）。

3.6. 与其他模型的比较

针对厌氧-缺氧-好氧工艺（A2/O）、SBR和氧化沟等不同的污水处理过程，研究者陆续提出了各种适合于特定环境仿真模型用来预测出水水质。如为预测屠宰场废水中NH4+-N的去除率，Kundu等[30]构建了基于进水水质和DO的BP神经网络模型。基于进水参数构建的ANN模型可预测好氧颗粒污泥的TN去除效率[31]。Ebrahimi等[32]提出了多变量回归模型预测氧化沟的出水生化需氧量（BOD）、TP浓度。然而，上述研究选择的输入参数主要为DO与进水水质，具有不可控性。与以往研究相比，本研究从仿真模型的可控性与预测精度两个方面出发，首次证实FFNN模型可采用实际可控参数（如表面气速和缺氧时间）代替不可控的DO实现出水总氮预测。为提高预测精度，采用多种算法对FFNN模型进行优化，SCG优化后的模型预测精度最高。在此基础上，将构建的模型与多种机器学习模型对比（表 5），结果表明经SCG算法优化的FFNN模型预测性能最佳，具有最小的RMSE和最高的R值。总的来看，研究构建的模型可根据进水水质变化调节可控运行参数，以保证出水TN处于稳定达标状态，同时有效避免过度曝气 [33]，降低系统运行能耗。

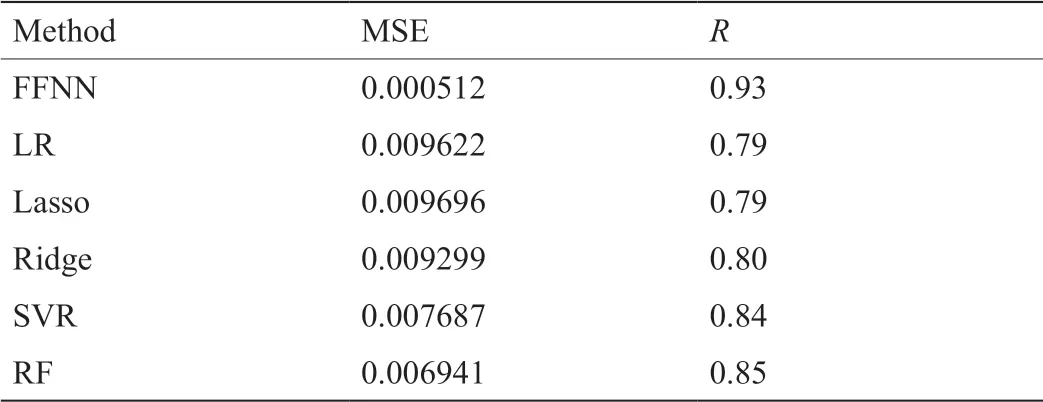
表5 不同预测方法的性能比较（R值四舍五入为小数点后两位数）

4. 结论

本研究基于主流SBR工艺构建了一种基于可控参数的前馈神经网络出水总氮预测模型，选择表面气速与缺氧时长代替DO作为FFNN模型的主要输入参数，运用长期仿真数据提高了模型可用可控性；选择SCG作为FFNN模型优化算法，实现出水TN及最佳运行参数的精准预测，可为污水处理系统的稳定运行及节能降耗提供有价值的解决方案。

致谢

本文得到了国家水体污染控制与治理科技重大专项（2017ZX07201003）、国家自然科学基金（51961125101）、浙江省重点研发计划（2018C03003）的大力支持。

Compliance with ethics guidelines

Zihao Zhao, Zihao Wang, Jialuo Yuan, Jun Ma, Zheling He, Yilan Xu, Xiaojia Shen, and Liang Zhu declare that they have no conflict of interest or financial conflicts to disclose.

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.eng.2020.07.027.