考虑材料微观结构的滚动接触疲劳寿命研究
黄彦彦,占煜村,杨建平,骆孝武,祝晋旋
(1.成都大学 机械工程学院,四川 成都 610106;2.东方汽轮机有限公司,四川 德阳 618000;3.四川大学 空天科学与工程学院,四川 成都 610065)
0 引 言
作为旋转机械的关键零部件,滚动轴承广泛应用于人造卫星、空间机械臂等航天装备中,其服役寿命对航天装备整体服役性能具有重要影响.疲劳失效是滚动轴承主要失效形式[1],对于安装正确、润滑良好的滚动轴承,其损坏形式一般为疲劳失效.根据Lundberg-Palmgren滚动接触疲劳寿命理论[2],接触应力是滚动接触疲劳寿命预测的重要参数.选取合适的材料模型,获取更为准确的应力分布,对于疲劳寿命分析结果具有显著影响.张若凡等[3]从疲劳强度、疲劳裂纹萌生与小裂纹扩展的微结构敏感性3个方面,对近年的研究成果进行了阐述,分析了金属材料在微结构性质、形态及分布等特征下的超长寿命疲劳行为与失效机理.因此,开展材料表征方法对滚动接触疲劳寿命预测影响的研究具有重要意义.
滚动轴承接触疲劳失效研究一直以来都是国内外研究者关注的热点问题.谢俊杰等[4]建立了考虑裂纹扩展的滚动接触有限元分析模型,对裂纹的扩展过程进行了模拟分析.蔡森等[5]基于Hertz接触理论,结合接触疲劳寿命曲线,对不同载荷和速度下的高铁轴承疲劳寿命进行了求解分析.金燕等[6]基于L-P疲劳寿命理论和Hertz接触理论,开展了温度对滚动轴承疲劳寿命影响规律的研究,得到了温度对轴承寿命具有显著影响的结论.孙玉凤等[7]结合ANSYS和Fe-Safe软件确定了滚动轴承最易发生疲劳失效的部位,并探究了残余应力深度对疲劳寿命的影响规律.然而,上述研究均基于材料的各向同性假设,而忽略了金属由许多细小的晶粒组成,在微观上具有各向异性力学行为这一基本事实.近年来,相关学者们从模拟轴承材料真实微观组织结构入手,开展滚动轴承疲劳寿命研究,得到了许多有益的成果.Raje等[8]利用Voronoi多边形对轴承钢多晶结构进行表征,分析了滚动轴承疲劳寿命具有统计学效应的微观机理.Paulson等[9]基于Voronoi多边形表征晶粒结构,结合弹流润滑(EHL)和有限元仿真,对EHL状态下的滚动轴承寿命进行了分析研究.Slack等[10]建立了基于Voronoi多边形的显式有限元模型,利用连续损伤理论对滚动轴承裂纹扩展行为进行了模拟仿真,并对轴承的寿命进行了预测.上述研究虽然引入了材料晶粒结构对滚动轴承接触疲劳寿命进行分析,但均基于晶体弹性假设,未对晶粒塑性的影响进行考虑.
本研究从微观角度出发,以Voronoi多边形表征马氏体轴承钢晶粒结构,采用ABAQUS有限元软件分别建立基于各向同性材料假设和考虑晶体学属性的滚动接触疲劳寿命分析模型,对两种材料表征方法下滚动轴承相对疲劳寿命进行预测分析,探究晶体学属性的滚动接触疲劳寿命分析模型的特性.在此基础上,开展晶粒尺寸分布对接触疲劳寿命分布的影响研究,评估晶体学属性滚动接触模型的疲劳寿命预测能力.
1 建模方法
1.1 晶体塑性本构

(1)

(2)
(3)
式中,hαβ为硬化模量,/MPa;qαβ为描述潜硬化行为的矩阵;h0为初始硬化模量,/MPa;τs为饱和临界分解剪切应力,/MPa;n为硬化系数.
1.2 晶体塑性有限元建模
1.2.1 赫兹接触建模
滚子与滚道的接触符合赫兹接触方式.为降低模型规模,减少模型的计算时间,本研究将滚动轴承模型简化为赫兹力加载的线接触模型.本研究所建立有限元模型晶粒总数为5 000个,且平均晶粒大小为10 μm[8],如图1(a)所示.模型中各组成晶粒其取向各不相同,晶粒取向通过Python随机数函数生成,共5 000种不同的晶粒取向,所建立有限元模型网格分布如图1(b)所示.模型采用平面应变单元CPE4,共222 111个单元,223 112个节点.模型边界条件根据轴承实际运行状态进行设置,即对AB、BC、CD 3条边自由度进行完全限制;AD边为自由接触表面,不限制其自由度.轴承钢主要成分为马氏体,本模型假设轴承钢完全由马氏体组成,不考虑残余奥氏体等组成成分的影响.马氏体力学性能参数如表1所示.滚道与滚动体的接触载荷P如图1(a)所示,可由式(4)计算得到,

表1 马氏体力学性能参数

(a)有限元网格分布
(4)
式中,Pmax为最大接触应力,为0.5 GPa;b为接触半宽,设为25 μm.
轴承钢晶粒尺寸发生变化,其强度和韧性将随之改变.总体而言,对于晶粒尺寸大于100 nm的金属,常温下晶粒尺寸越小,其强度越高、疲劳性能越好[13].本研究以平均晶粒尺寸为10 μm的马氏体轴承钢为研究对象,引入晶体塑性开展滚动轴承疲劳寿命研究,并与基于各向同性材料假设的模型分析结果进行对比分析.弹性模量和屈服强度为各向同性材料模型建模时的必要参数,为准确确定上述材料参数,建立了平均晶粒尺寸为10 μm的马氏体薄板拉伸试验有限元分析模型.所建立有限元模型网格分布如图2所示,模型共有85 330个单元,104 904个节点,单元类型为C3D8.采用一端固定,一端以1.125 μm/s的速度移动的方式进行拉伸试验.

图2 马氏体多晶拉伸试验模型
有限元分析得到的加载端力—位移曲线,经过一定的换算可以获得相应的应力—应变曲线,如图3所示.通过对应力—应变曲线弹性变形阶段斜率的计算,得到马氏体薄板弹性模量约为362 GPa,计算值与文献[14]实验测得值一致,说明了模型的有效性.由图3可知,通过模型得到的应力—应变曲线没有明显的屈服点.因此,本研究采用工程上常用的σ0.2对材料屈服强度值进行估算,屈服强度约为1 350 MPa.
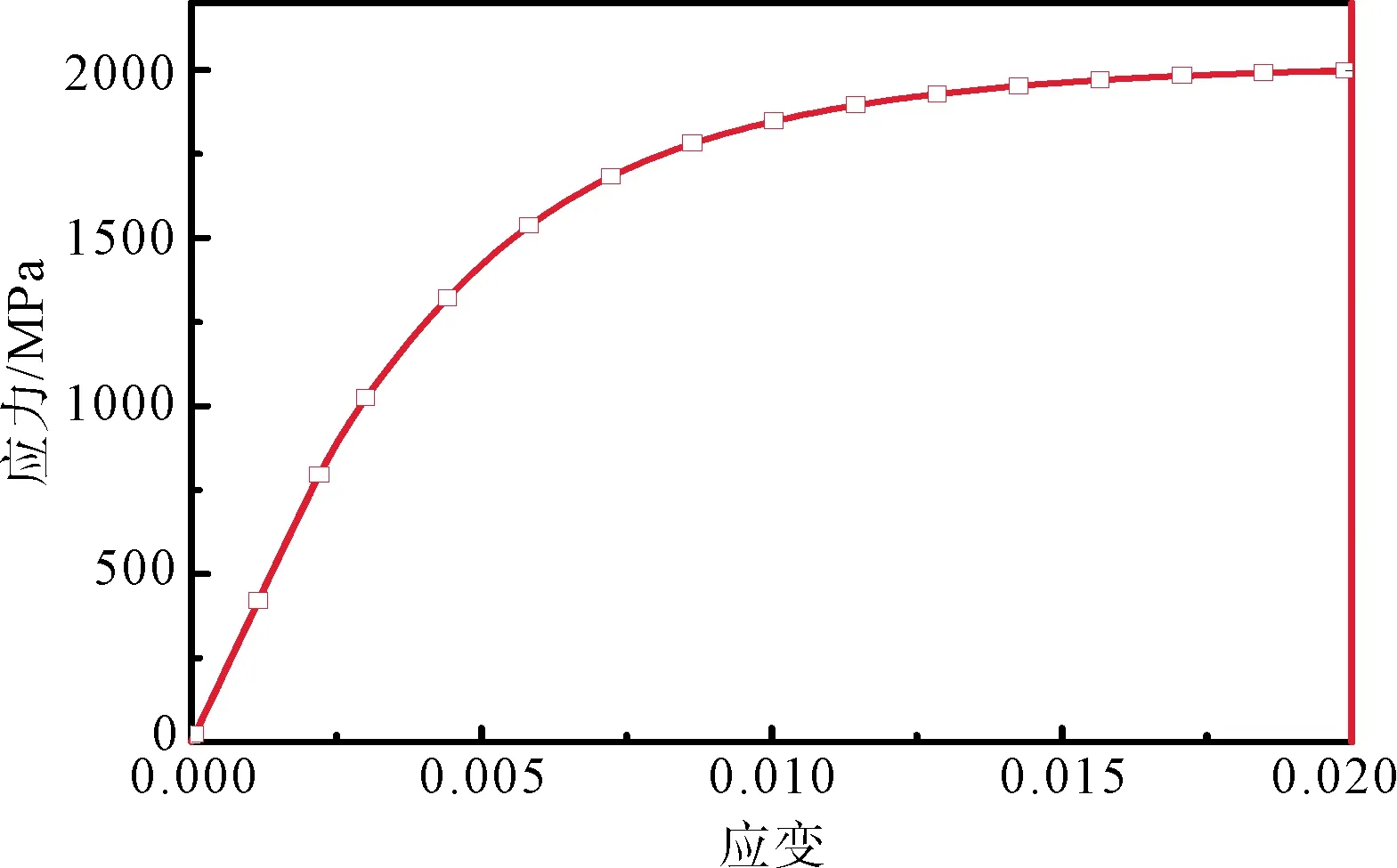
图3 拉伸试验应力—应变曲线
2 结果与讨论
2.1 应力分布
图4所示为Pmax为0.5 GPa时,基于各向同性材料假设和考虑轴承钢晶体学属性模型的下表面等效(Eguivalent)应力分布情况.由图4可知,两种情况的应力分布趋势基本一致,最大von Mises应力均出现在下表面某处,而不是位于接触表面.同时,基于各向同性材料假设的模型其应力过渡十分平滑,而对于考虑晶体学属性的模型,其应力分布呈现出一定的离散性.由于组成材料各晶粒取向各不相同,当受力方向相同时,每个晶粒将表现出不同的应力状态,最终导致整体应力表现出一定的离散状态.此外,从图4中还可以看出,考虑晶体学属性的模型其最大von Mises应力值要高于基于各向同性材料假设的模型,这主要是由晶界处所产生的应力集中造成的.
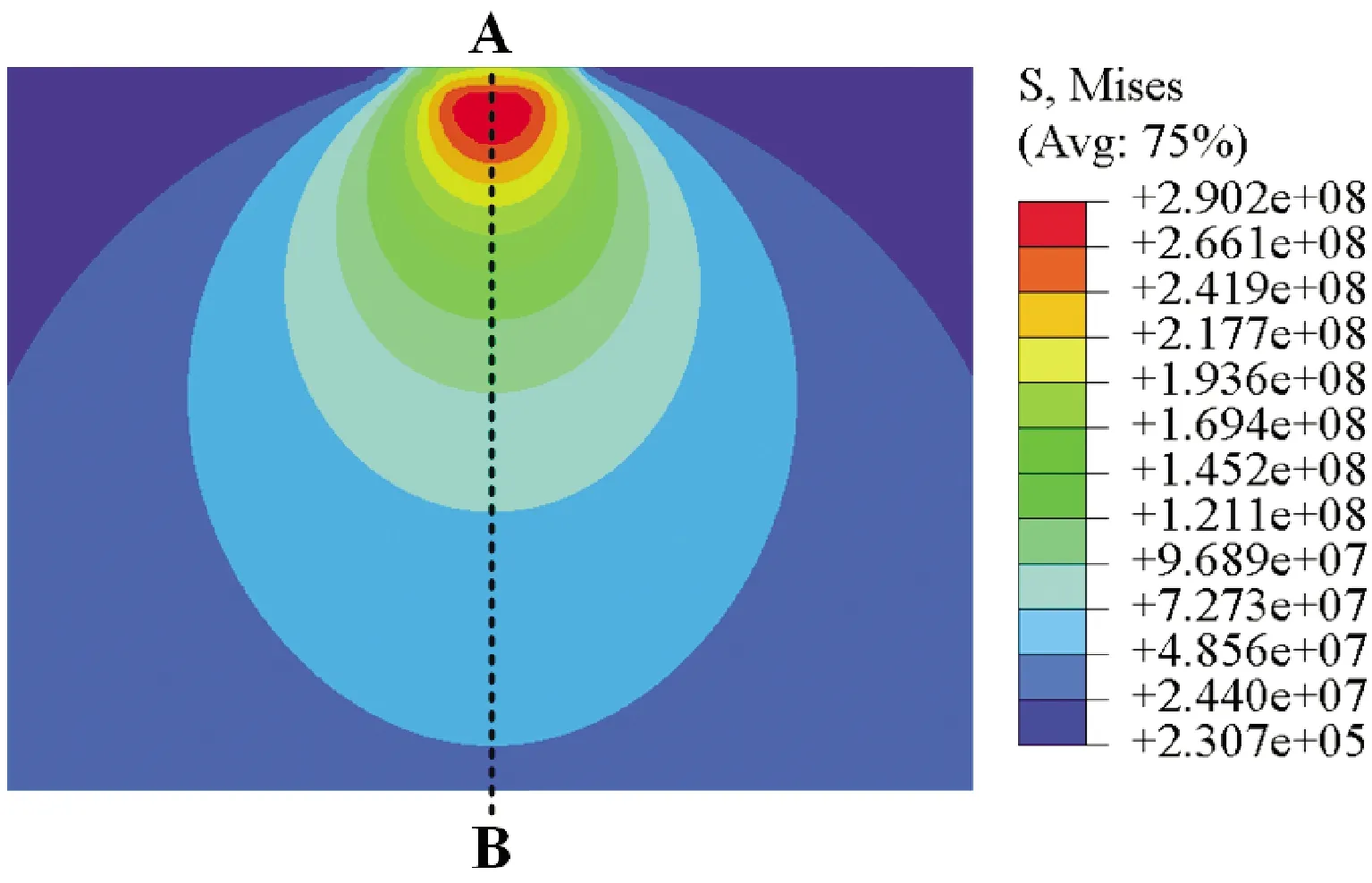
(a)各向同性材料
图5给出了von Mises应力沿赫兹接触中心线AB、CD的变化情况.由图5可知,对于基于各向同性材料假设的模型和考虑晶体学属性的模型,两者的von Mises应力值均呈现出迅速增大到最大值,然后逐渐减小的规律,且二者应力最大值发生位置基本重合.此外,AB、CD线上相应位置处的整体应力值并无明显差别,说明考虑晶体学属性的模型,整体上同样满足赫兹接触应力分布.对于基于各向同性材料假设的模型,其von Mises应力变化十分平滑,而对于考虑晶体学属性的模型,由于晶粒取向不同的影响,应力变化呈现出剧烈振动的现象.
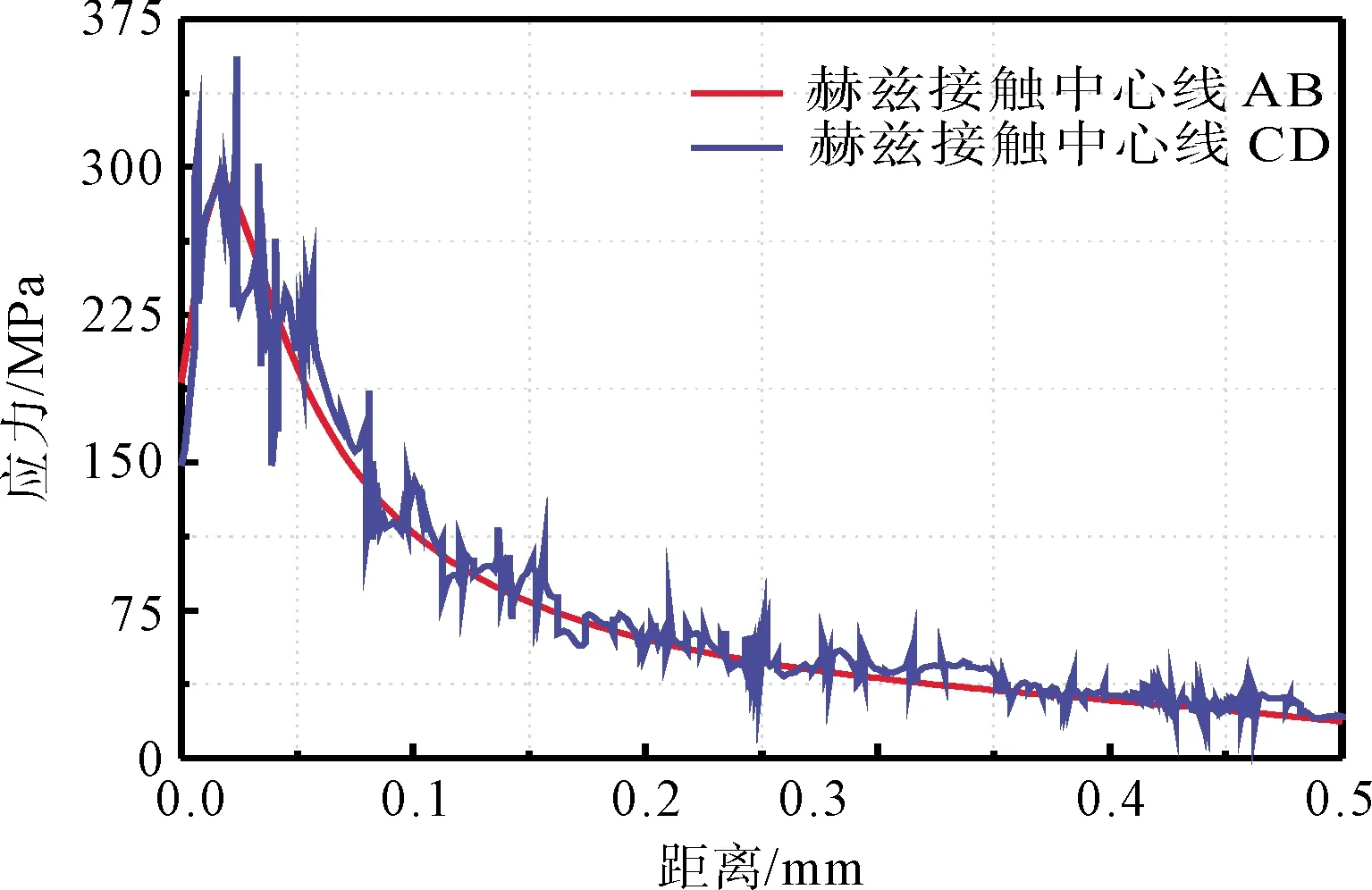
图5 赫兹接触中心线von Mises应力
2.2 寿命分布
滚动轴承寿命存在多种预测方法,如Lundberg等[2],Ioannides等[15],Zhou[16]和Zaretsky[17]等提出的方法.其中,Lundberg等寿命预测模型应用最为广泛,且其有效性已被大量实验所验证.因此,本研究选取Lundberg方法对滚动轴承接触寿命进行评估.Lundberg滚动接触疲劳寿命预测模型如下,
(5)
式中,S为材料生存概率;N为疲劳寿命循环数,/次;e为Weibull斜率;c为应力指数,τ为临界剪切应力,/MPa;z为最大应力发生位置深度,/mm;V为体积应力,/MPa;A、c、h为由实验确定的材料常数.对于轴承钢,c和h分别取为10.33和2.33.由上式可知,生存概率S与临界应力值成反比,与出现最大应力的深度成正比.因此,式(5)可简化[8]为,
N∝zr/τq
(6)
式中,∝表示两个变易为正比例关系.为方便起见,假设指数q和r与c和h相同,即r为2.33,q为10.33.
建立9个考虑晶体学属性的赫兹接触模型,对其应力分布进行提取,并利用式(6)对接触疲劳寿命进行预测.为便于与基于各向同性材料假设的模型进行对比,本研究以相对寿命表征滚动轴承疲劳寿命.图6为基于各向同性材料假设模型与考虑晶体学属性模型预测的滚动轴承相对疲劳寿命.由图6可知,对于考虑晶体学属性的模型,其预测的轴承平均寿命不到基于各向同性材料假设模型的三分之一.由于基于材料各向同性假设的模型未考虑晶粒间的应力集中效应,所以其预测的疲劳寿命相较考虑晶体学属性的模型偏大.从图6中还可以看出,9个考虑晶体学属性模型预测的相对疲劳寿命并不完全一致,这是由于材料具有不同的微观结构,应力分布不均匀造成的.相较于基于各向同性材料假设的模型,考虑晶体学属性的模型具有能够分析寿命统计性分布的优点.

图6 滚动接触相对疲劳寿命
2.3 累积塑性剪切应变
对于各向同性材料模型,当外力不足以使材料产生大于屈服强度的应力时,塑性变形便不会发生.本研究的马氏体屈服强度为1 350 MPa.显然,采用Pmax=0.5 GPa不足以使马氏体轴承钢产生塑性变形.图7(a)为Pmax=2.0 GPa时考虑晶体学属性模型的累积剪切应变状态.由图可知,当Pmax为2.0 GPa时,材料内部会产生一定的塑性应变,最大累积剪切应变值为1.030×10-3(应变为形变量与原尺寸比,无量纲).当Pmax为0.5 GPa时考虑晶体学属性模型的累积剪切应变状态如图7(b)所示.与基于各向同性材料假设的模型不同,即使外力大小未达到能使材料产生塑性变形的程度,材料内部仍有极小(相对于2.0 GPa的情况)的累积剪切应变产生.

(a)Pmax=2.0 GPa
综上所述,相对于基于各向同性材料假设的模型,考虑晶体学属性的模型能够更好地对材料塑性变形行为进行分析.
2.4 晶粒尺寸分布对接触疲劳的影响
晶粒的尺寸分布具有随机性,但总体上符合正态分布规律.本研究将讨论晶粒尺寸分别在N(0.01 mm,1×10-8mm2)、N(0.01 mm,2.5×10-7mm2)、N(0.01 mm,1×10-6mm2)、N(0.01 mm,2.5×10-5mm2)和N(0.01 mm,1×10-4mm2)5种正态分布情况下马氏体钢的疲劳寿命分布情况,以进一步说明考虑晶体学属性的滚动接触疲劳模型在分析疲劳寿命离散性上的优势.
将上述5种晶粒尺寸分布下得到的21个临界应力及位置深度带入式(6)中,得到相应的相对寿命,并将其拟合得到Weibull寿命曲线,如图8所示.由图8可知,晶粒尺寸分布的方差越小,对应的Weibull斜率越大,马氏体钢的寿命分布范围越小,说明晶粒的均匀分布程度与疲劳寿命密切相关.晶粒分布越不均匀,晶界处产生较大应力集中的可能性越大,在很大程度上将降低材料的疲劳寿命.
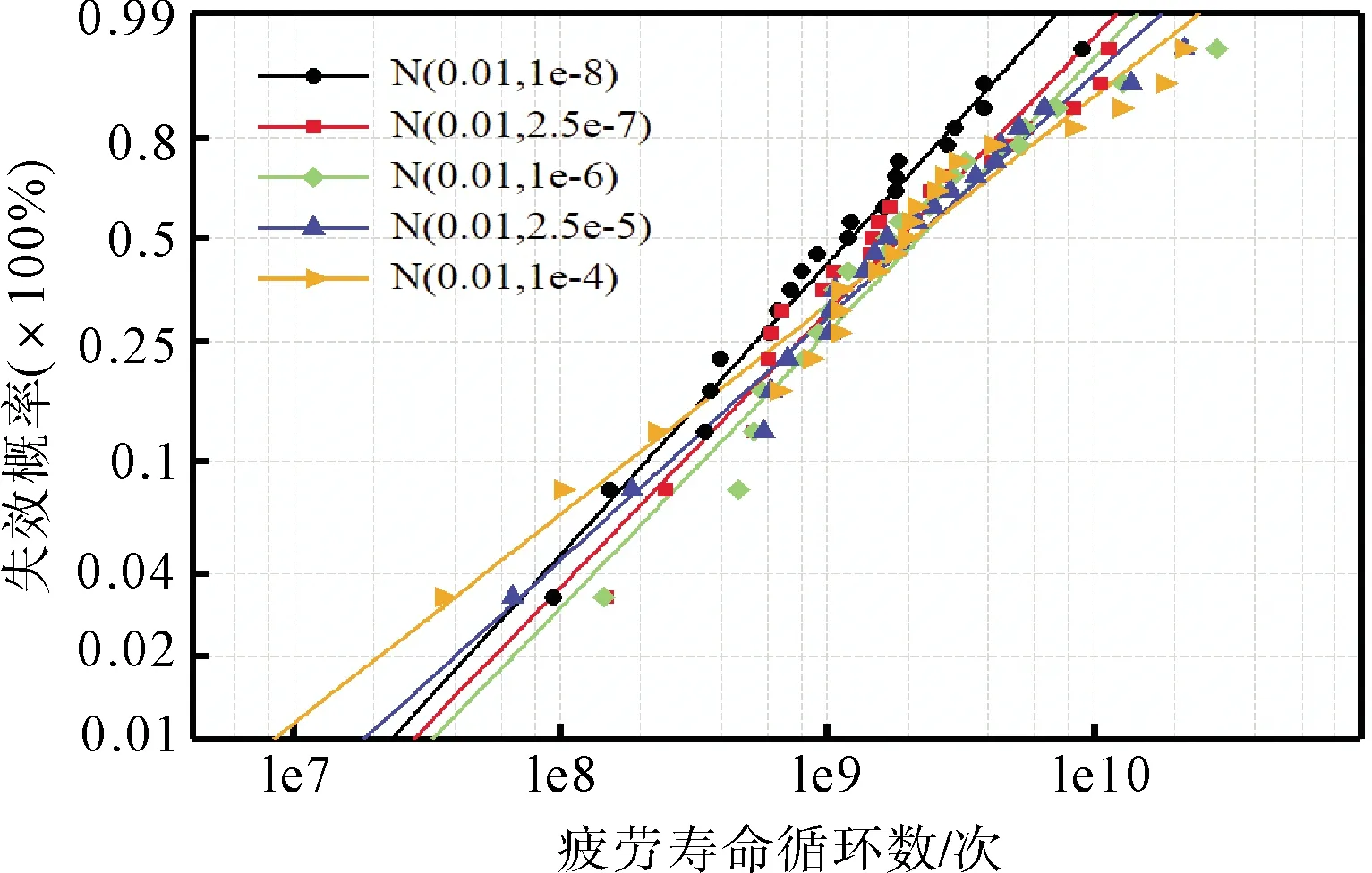
图8 不同晶粒尺寸分布下马氏体钢的接触疲劳寿命分布
3 结 论
1)考虑晶体学属性的模型计算出的von Mises应力要大于基于各向同性材料假设的模型的应力,且von Mises应力分布的离散性要高于基于各向同性材料假设的模型应力分布的离散性.
2)考虑晶体学属性的模型其预测的接触疲劳寿命不到基于各向同性材料假设模型疲劳寿命的三分之一,且能够对滚动轴承寿命分布的统计性进行模拟表征.
3)在外力引起的应力小于材料屈服强度时,考虑晶体学属性的模型仍能产生一定的塑性变形.
4)晶粒尺寸分布离散性越大,威布尔斜率越小,即接触疲劳寿命具有更大的分散性.

