平动非惯性质心参考系动力学规律的应用

刘传跃

(邹平市第一中学,山东 滨州 256200)

1 平动非惯性质心参考系的动力学规律

如图1所示,建立固连于地面的静止惯性参考系S,以质点系统的质心为原点建立质心参考系S′.当质心参考系S′具有平动加速度aC时,则该系称为平动非惯性质心参考系.

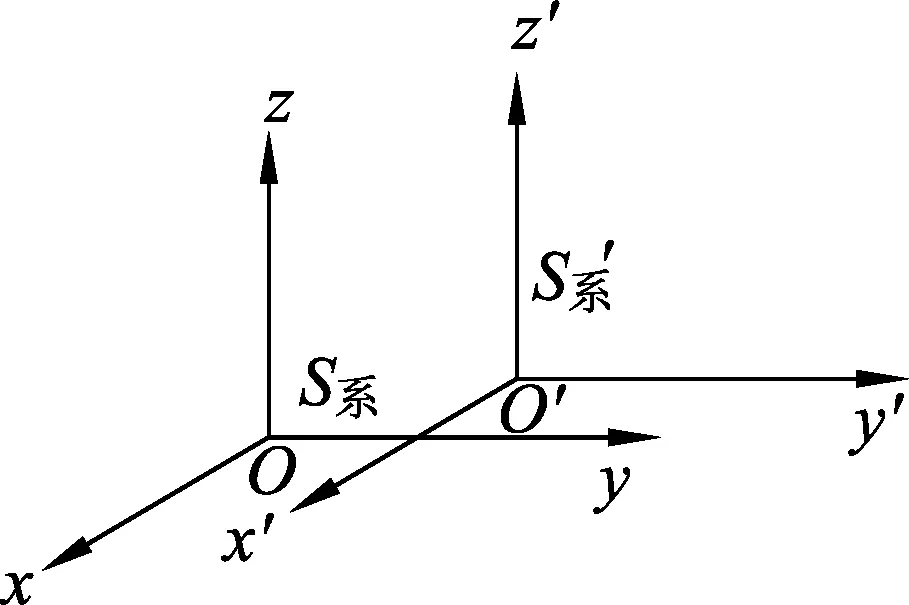
图1 平心非惯性质心参考系

下面讨论在平动非惯性质心参考系中的动力

学规律.

1.1 质点的动力学方程

对质点系统中第i个质点,设其质量为mi,则该质点在质心参考系中的动力学方程为

(1)

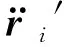
1.2 平动惯性力对质心的力矩和作用点

第i个质点受到的平动惯性力为fi=-miaC,其中aC为系统质心的加速度.由此可知,每个质点受到的平动惯性力的大小与其质量成正比,方向均与质心参考系的加速度aC反向.在质心参考系中各质点所受平动惯性力对以质心为参考点的力矩矢量和为

MC′=∑(ri′×fi)=-∑(miri′)×aC=0,

即有

MC′=0.

(2)

该式说明,在平动非惯性质心参考系中各质点受到平动惯性力的合力矩为0.平动惯性力的合力f=-∑miaC不为0,其作用点为质心,但并不意味着各质点受到的惯性力矩不做功.

1.3 质点系统的动能定理

在惯性参考系中对质点系统考虑柯尼希定理,由动能定理,得

∑Fi外·dri+∑Fi内·dri=

(3)

dri=drC+dri′,

(4)

式中dri′为第i个质点在质心参考系中的位移,将(4)式代入(3)式,得

∑Fi外·drC+∑Fi内·drC+∑Fi外·dri′+

∑Fi内·dri′=

(5)

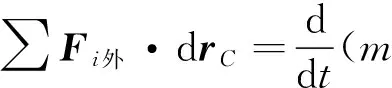
利用该式消去(5)式左侧第一项和右侧第一项.若系统内任意一对内力作用点的相对位移为0,则会使该对内力所做总功为0.因(5)式中左侧第二项为系统内力对质心做功的代数和,故在任意参考系中该值为零.则(5)式最终为

∑Fi外·dri′+∑Fi内·dri′=

即有

∑Ai外′+∑Ai内′=∑ΔEk′.

该式说明,在质心参考系中质点系统总动能的增量,等于所有外力对各质点所做的功与所有内力对各质点所做的功之和.这就是质心参考系中质点系统的动能定理.该式与惯性系中的系统的动能定理在形式上保持一致.

1.4 质点系统的角动量定理

在惯性参考系中,系统相对于固定参考点O的角动量为

(6)

第i个质点相对质心的关系有

(7)

将(7)式代入(6)式,得

(8)

将(8)式对时间求导,得

mrC×aC.

(9)

系统中各质点受到的外力相对参考点O的力矩

∑Mi外=∑ri×Fi外=∑ri′×Fi外+

∑rC×Fi外=∑ri′×Fi外+mrC×aC.

(10)

由惯性参考系中的系统角动量定理

(11)

联立(9)-(11)式,得

即有

(12)

该式表明,质点系统对质心的角动量的变化率,等于所有外力对质心的合力矩.这就是质心参考系中质点系统对质心的角动量定理.尽管质心参考系不一定是惯性系,此式在形式上却与惯性系中的角动量定理形式一样.

2 平动非惯性质心参考系的应用

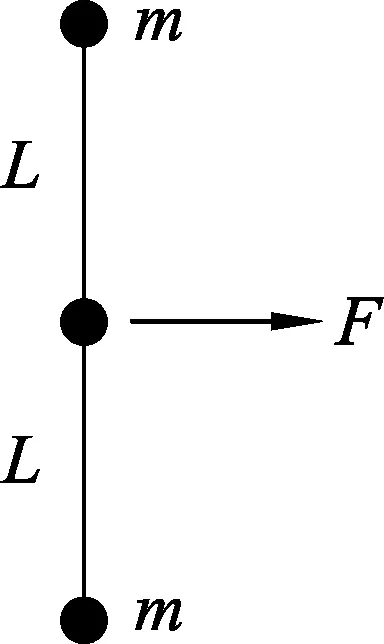
图2 初始状态

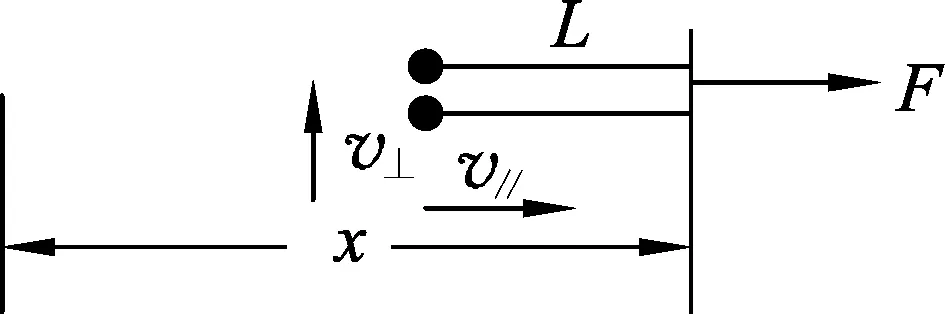
图3 第1次相碰前瞬间

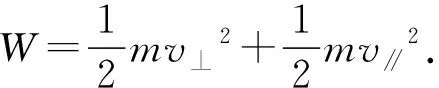
以上两式涉及4个未知量,故求解需要寻找其他关系.又轻绳对两小球做功W和冲量I在静止参考系中不易求出,可考虑在平动非惯性质心参考系中讨论问题.

图4 过程中的某个状态

解答:以系统质心C为原点建立平动非惯性质心参考系,如图4所示.设在过程中的某个状态,轻绳与竖直方向夹角为φ,在质心参考系中质心始终处于两小球连线中点,由于质心参考系为零动量参考系,故图4中两小球的速度等大反向.

以轻绳中点O′为研究对象,因其质量为0故所受合力为0,有2Tsinφ=F,小球到质心距离h=Lcosφ,取微分有dh=-Lsinφdφ,轻绳对两小球的元功dW=2Tcosφdh,联立以上各式得dW=-FLcosφdφ,对整个过程积分有

得轻绳对两个小球做的总功为W=FLsinφ.

在质心参考系中,对系统应用动能定理,得

(1)

则有

(2)

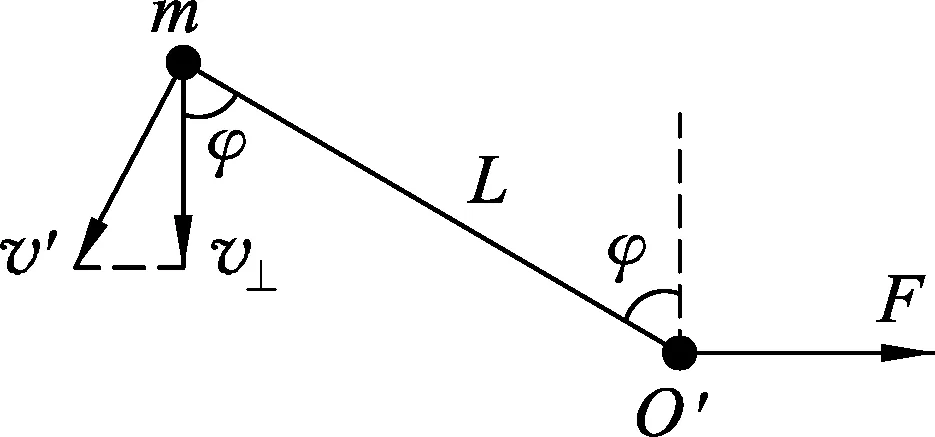
图5 小球绕轻绳中点O′转动

第1次相碰时φ=π/2,则有

(3)

如图5所示,小球绕轻绳中点O′逆时针转动,设夹角为φ时小球速度为v′,在质心参考系中由速度合成定理,得

v′sinφ=v⊥，

(4)

在dt时间内小球绕轻绳中点O′转过角度dφ,则有

v′dt=Ldφ，

(5)

联立(2)、(4)、(5)式,得

对整个过程积分,得

(6)

在静止参考系中,对系统应用动量定理,则有

Ft=2mv∥.

(7)

联立(6)、(7)式,得

(8)

点评:解题的关键是在平动非惯性质心参考系中的讨论,一方面解决了轻绳对小球拉力做功的问题,另一方面将小球和轻绳中点O′之间的部分视为刚体,构建小球绕中点O′的转动模型,得出绕行过程的微分方程,通过积分得到整个过程的时间,为应用动量定理提供了条件.

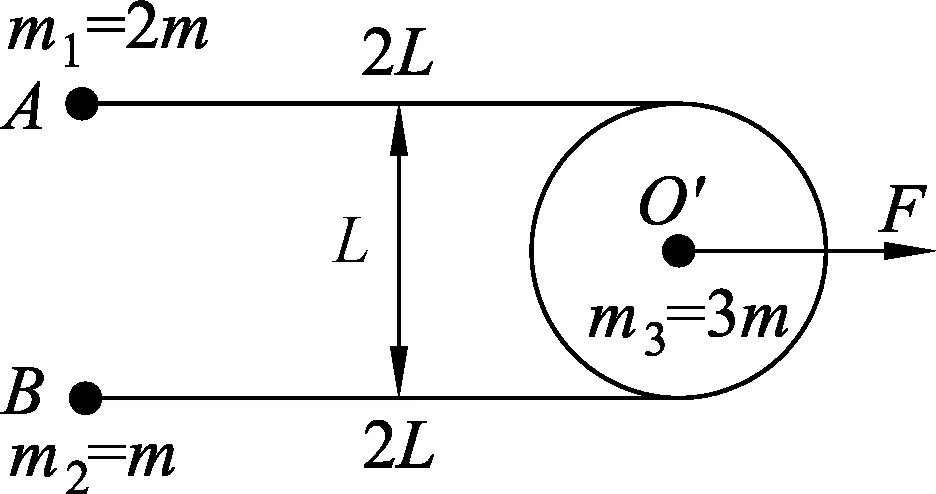
图6 初始状态

例2.如图6所示,在光滑水平面上放置质量分别为m1=2m、m2=m的小球A和B,以及直径为L、质量为m3=3m的平放着的匀质圆盘,两个小球和圆盘边缘部位用长为2L的两根平行轻杆固连在一起,组成一个刚体系统.开始时系统静止,在圆盘中心O′处施加一个与轻杆平行的水平恒力F,不计一切摩擦.

(1) 说明此刚体系统将会发生摆动,并求摆动的最大夹角φ0；

(2) 若考虑φ0较小的情况,试求刚体系统的摆动周期T0.

分析:题目描述的是质量分布不均匀的刚体系统,外力F的作用线并不通过系统质心,若选择在静止参考系中完全分析刚体的运动较为困难,不过考虑到刚体系统的质心在水平恒力作用下做匀变速直线运动,选择非惯性质心参考系讨论该问题不失为一种思路.

解答: (1) 以A和B两球连线中点为原点,x轴正方向通过圆盘中心水平向右,建立坐标系.设刚体系统质心C的位置如图7所示.由质心定义,得系统的质心坐标为

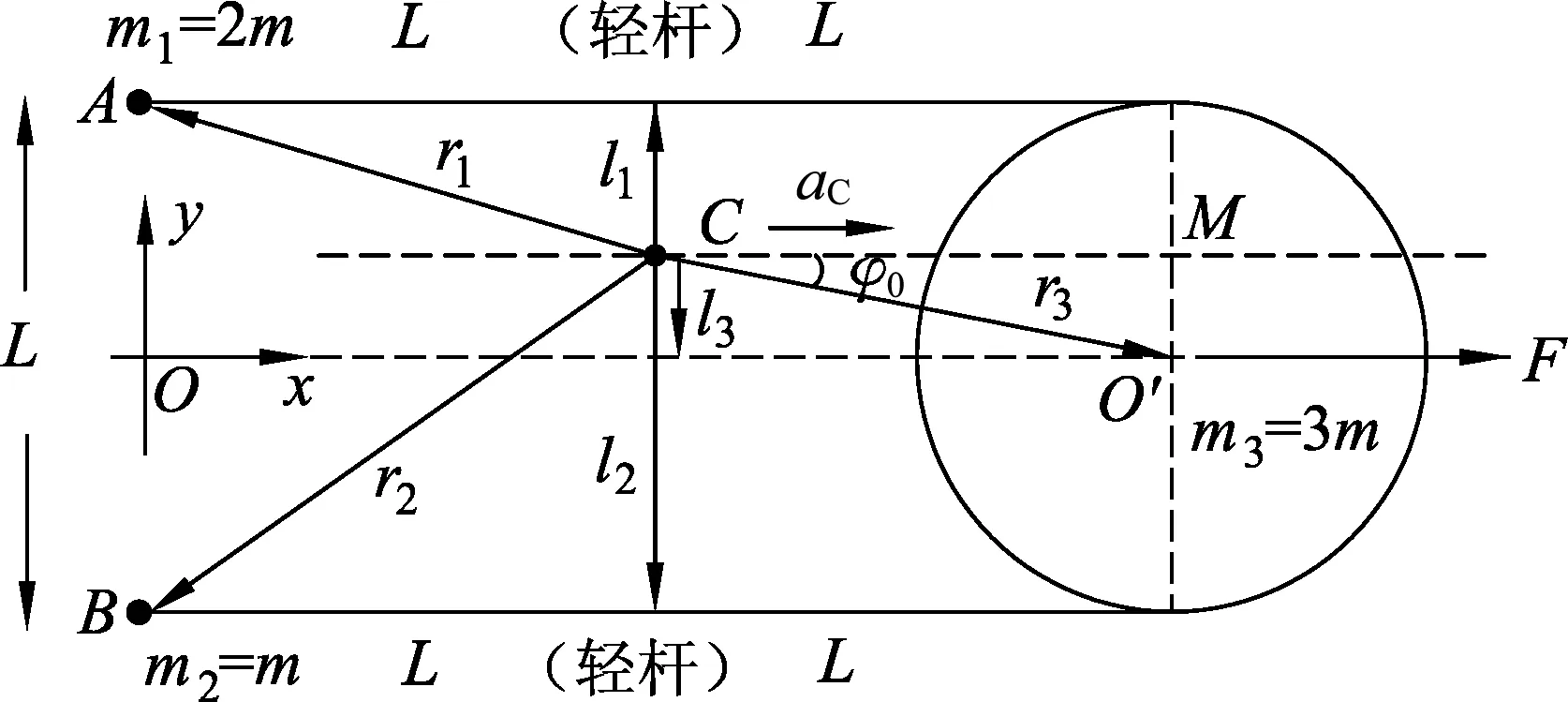
图7 质心位置

(1)

(2)

在静止参考系中,对刚体系统应用质心运动定理,得

(3)

即系统质心C沿着水平向右的方向做匀加速直线运动,且始终位于CM直线上.

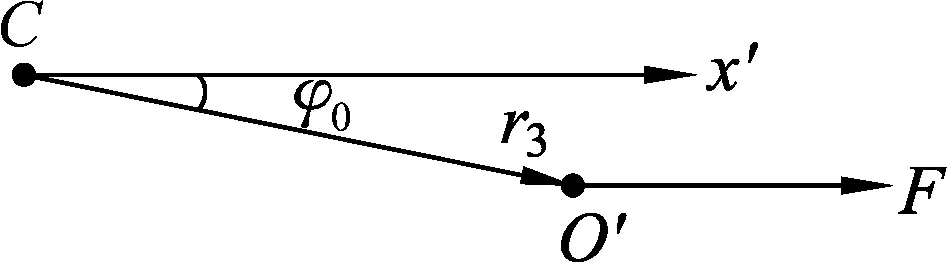
图8 圆盘中心O′绕质心C摆动

以质心C为坐标原点,x′坐标轴与x坐标轴平行,建立随系统质心运动的非惯性质心参考系.设O′C与x′轴的夹角为φ0,以顺时针为夹角正方向.如图8所示.

在质心参考系中,外力F作用于圆盘中心O′,相对质心C产生力矩,对刚体系统应用角动量定理可知,初始时F的力矩为逆时针,使系统绕质心C逆时针加速转动,夹角φ0减小,角速度逆时针增加,当夹角φ0减为0时,由于角速度不为0圆盘中心将越过x′坐标轴,之后F的力矩变为顺时针,使系统逆时针减速转动直至角速度为0.对刚体系统应用动能定理,可知在该过程中外力F先做正功后做负功,其值等大异号,故此时O′C与x′轴的夹角大小仍为φ0.与以上过程类似,之后系统顺时针先加速转动再减速转动,直至角速度为0回到图8状态.之后再重复上述过程.

综上所述,系统将发生摆动,摆动的最大夹角为

(2) 在质心参考系中,设摆动过程中任意夹角φ,对刚体系统应用角动量定理,得

(4)

式中IC为刚体对质心的转动惯量.

如图7所示,质心C到上方轻杆、下方轻杆和直线OO′的距离为

(5)

由几何关系,得质心C到小球A、B和圆盘中心O′的距离为

(6)

由转动惯量定义和平行轴定理,联立(6)式,得

(7)

考虑到最大夹角φ0为小角度,故刚体系统的摆动可视为绕质心C的简谐运动,联立(4)、(7)式,得简谐运动方程

(8)

式中圆频率

摆动周期

点评:静止参考系中刚体的复杂运动,在非惯性质心参考系中看来却如此简单,正是质心参考系中质心静止不动这一独特性质的反映.在应用角动量定理、动能定理等动力学规律时不需要考虑惯性力的影响也源于此.