GeoGebra软件在物理可视化教学中的应用

刘健智 程 婷

(湖南师范大学物理与电子科学学院，湖南 长沙 410081)

1 GeoGebra软件与可视化教学

GeoGebra软件可以代替传统板书呈现一些无法板书或板书不清的复杂情境，甚至呈现3D效果，训练学生的空间思维能力；可以呈现动态变化的过程，构建物理模型，加深学生对物理规律的理解；亦可以展示科学推理的过程，使得思维方法更加形象、具体……这些都有利于解决物理学科的抽象性问题，利用视觉思维提升学生的感性认识，增强物理教学的可视化.[1-3]

2 在平抛运动中的具体应用

平抛运动是学生在高中阶段接触的第一种曲线运动，也是后面分析带电粒子在电磁场中运动的基础，在高中物理体系中具有重要地位.利用GeoGebra软件辅助平抛运动的可视化教学主要可体现在数据处理、规律推导以及临界过程分析3个方面.

2.1 数据处理的可视化

2017年版课程标准要求“通过实验，探究并认识平抛运动的规律”.[4]在2019新人教版高中物理教材的平抛运动实验中，只涉及平抛运动水平和竖直方向运动规律的探究，未提及平抛运动的轨迹特点.[5]笔者利用GeoGebra软件的拟合功能丰富数据处理，探究平抛运动的轨迹特点.

利用传感器和计算机获得平抛运动的水平位移和竖直位移如表1所示.[5]打开GeoGebra软件(笔者使用的版本为GeoGebra classic 5)，在表格区输入数据.其中，数据小数位或有效数字可通过精确度进行设置.需要说明的是，如果最后一位或几位小数为0，系统会自动舍去，无法实现数据格式的统一，但并不影响拟合结果.

表1 传感器获得的平抛运动的轨迹数据

将数据创建为点列，粗略还原平抛运动的实际轨迹.猜想其为抛物线，则应满足一元二次函数的解析方程.考虑抛出点为坐标原点，解析形式应为f(x)=ax2.利用“fit”指令将点列拟合成f(x)同样形式的函数g(x).由于g(x)只是软件计算出的最匹配点列的函数，因此并不是所有的点都会满足该函数方程.从图1可以看出，点列与二次函数图像基本吻合，说明猜想合理.

图1 GeoGebra软件y-x拟合函数图像

为了进一步提高结论的可信度，利用“rsquare”指令计算点列与g(x)的相关系数为r=0.986.说明在误差允许的范围内，平抛运动轨迹确实是一条抛物线.用同样的方法也能计算点列与一次函数(r=0.925)、三次函数(r=0.866)甚至其他函数的相关系数，但从数值上看只有二次函数的相关系数最高，从侧面反映点列最符合二次函数关系，使学生养成严谨的科学态度.

在此基础上，利用GeoGebra的代数运算功能，可直接计算初速度的大小.如果是利用频闪照相的方式探究平抛运动规律，保证每两个点间隔时间相同，还能实现平抛运动y-x到y-t、x-t图像的转化，渗透运动的合成与分解思想；若再利用多项式拟合，就能直接从y-t、x-t图像中分析出竖直和水平方向的运动规律，十分方便.

2.2 规律推导的可视化

平抛运动有两条重要推论，一是速度偏向角的正切值为位移偏向角正切值的两倍，二是速度延长线一定过水平位移的中点.日常教学多是从代数关系入手讲解，过于抽象枯燥.利用GeoGebra软件，一是比黑板作图更加规范；二是能直接显示如水平位移中点、速度延长线与x轴交点的位置坐标，更加直观；三是能将规律动态化，证明这两条规律在平抛运动的任何位置都成立，趣味性更强.下面是利用GeoGebra软件进行规律推导的具体操作.

图2 平抛运动的两条推论

输入函数“f(x)=ax2/(x≥0)”，表示平抛运动轨迹.a值与初速度有关，决定抛物线的弯曲程度.构建x、y轴，并在抛物线上描出一点(D点)，作为研究对象.过该点表示速度、位移，并构建速度矢量图.利用工具栏做出水平位移中点及速度延长线与x轴的交点.通过属性设置，隐藏一些不必要的点或线，并对颜色、线型、线径、是否显示等进行修改，突出主要信息.如图2所示，移动D点，可发现水平位移的中点J与速度延长线与水平位移的交点K始终重合，位置坐标也保持一致，说明速度延长线确实过水平位移的中点.

在此基础上，进一步探究速度偏向角与位移偏向角正切值的大小关系.如图2示，符号b表示速度偏向角与位移偏向角正切值的比值.移动D点，可见b值始终为2，说明速度偏向角正切值始终为位移偏向角正切值的两倍.

2.3 临界过程分析的可视化

平抛运动的临界值问题主要存在于斜面及乒乓球、羽毛球等球类运动过网模型中，分析清楚整个运动情境，找到运动过程的临界条件，往往就是解题关键.下面以2015年理综全国卷Ⅰ第18题为例，谈谈如何利用GeoGebra软件构建物理模型进行可视化分析，更好抓住解题关键.

图3 乒乓球过网模型

一带有乒乓球发射机的乒乓球台如图3所示.水平台面的长和宽分别为L1和L2，中间球网高度为h，发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距台面高度为3h.不计空气的作用，重力加速度大小为g，若乒乓球的发射速率v在某范围内，通过选择合适的方向，就能使乒乓球落到球网右侧台面上，则v的最大取值范围是

图4 临界条件1-不触网情形

本题容易出错的地方是对临界条件2的判断，学生容易误认为临界条件是轨迹过J点.[6]这是因为学生缺乏空间想象力，没有意识到v0方向的任意性.利用GeoGebra的3D视图使物理情境立体化、直观化，能够帮助学生顺利突破这一误区.在此基础上，还能改变题给条件，给出L1、L2、h的具体值，要求计算v0的范围，或是探究L1、L2、h变化对v0和轨迹的影响.GeoGebra软件能对学生的计算结果进行检验，并直观呈现某条件改变后的影响，强化学生对这一类问题的理解.

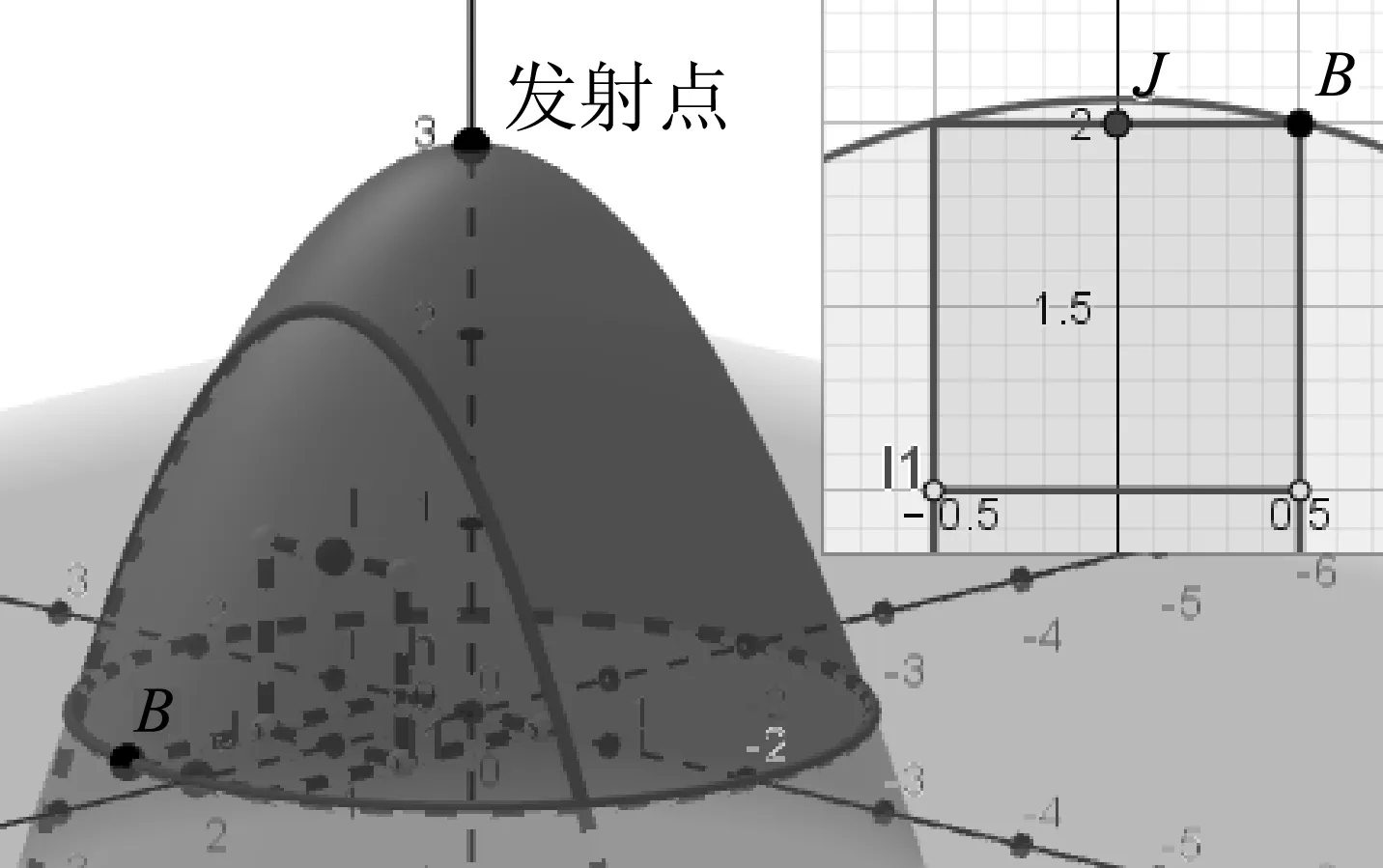
图5 临界条件2-不出界情形

3 在其他教学中的应用

3.1 用于抽象概念的形象化

相对于初中阶段，高中阶段的物理更加抽象，学生在学习过程中存在很多的认知困难.如果不能及时解决这些问题，就会导致学生越学越不懂，渐渐丧失学习兴趣.利用GeoGebra软件能将抽象概念的推导或者理解过程用图像、动画等方式呈现，增强学生对抽象概念的形象认知，帮助理解.

例如在电势的教学中，两个电荷周围电势的叠加是教学的难点，这时可利用GeoGebra软件的3D绘图区，通过输入两电荷周围的电势在空间满足的方程，呈现电势的分布情况，使学生获得感官认识.选择不同的视图可观察不同方向上电势的分布特征，而对滑动条进行设置还能实现参数的动态调节，显示如等量同种、异种电荷的三维电势分布，使电势具象化.[7]由于z轴代表电势，则“z=某一具体值”的平面与电势分布面的交线即为等势面，还能强化学生对于等势面的理解.

3.2 用于复杂规律的直观化

物理规律的教学应着重体现规律背后的思维方法，而这往往较为抽象，且当中可能包含复杂的数学推导，加大了规律教学的难度.这时可以考虑利用GeoGebra软件将思维方法具体化、数学推导简单化，使物理规律变得更加直观.如在匀变速直线运动位移与时间关系的推导中，微元法和极限思想是教学的重点，可以利用GeoGebra软件展示科学推理的过程，增强思维的可视化.

做出匀变速直线运动的v-t图像，选定研究区间并划分为n段.已知匀速直线运动中矩形面积可以表示位移.将每小段视为以该段初速度运动的匀速直线运动，利用“lowersum”指令计算下和值，可粗略表示研究区间的位移.由于每段的实际速度大于或等于该段的初速度，下和值相对于实际位移值应偏小.将每一小段视为以该段末速度运动的匀速直线运动，利用“uppersum”指令计算上和值，同理该值相对实际值应偏大.实际位移总介于上和值与下和值之间，采取二者逼近的方法计算实际位移.[8]

增大n值，下和值增大，上和值减小，均更接近实际位移.当设置的n值较大，两种矩形构成的图形几乎就是梯形，则梯形面积可代表矩形面积，进而代表位移.利用“integral”指令计算图像面积进行验证，可见图像面积始终介于上、下和值之间，且n值较大时三者几乎无差别，说明匀变速直线运动的位移确实可以用梯形面积表示.

输入的初速度、加速度及矩形数量均可通过滑动条进行设置，表明该结论具有普遍性，适用于所有的匀变速直线运动.而通过同样的方法也能对非匀变速直线运动进行探究，弥补实际教学中不规则图形面积暂时无法计算的遗憾，加深学生对v-t图像面积含义的理解.

除此之外，像力的合成与分解，重力与万有引力的关系，两电荷周围场强的叠加等复杂规律，也都能利用GeoGebra软件辅助讲解，简化、直观.

3.3 用于物理过程的动态化

物理过程往往具有动态性，这时仅通过文字、语言，亦或是图片难以准确描述其特征，而学生也需要一定的想象力才能理解并还原整个过程，具有一定难度.利用GeoGebra软件的动态交互功能能对物理过程进行动态模拟，增强情境的真实性.

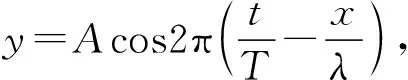
例如双星系统的运行.双星系统是指两个相距较近，只在彼此引力作用下做圆周运动的恒星组成的系统.前面学生接触到的都是围绕中心天体的星体转动，无法理解像双星系统这样围绕连线上某一点的转动.利用GeoGebra制作动画直观呈现双星系统的运行机制，便于学生突破这一难点.

除此之外，像追及相遇问题、带电粒子在电磁场中的运动，甚至是复杂的交流电的产生，也都能利用GeoGebra软件制作动态变化的效果，帮助理解.

3.4 用于实验探究的可视化

物理是一门以实验为基础的学科，物理中概念规律的建立或多或少都有一定的实验基础.利用GeoGebra软件增强实验探究的可视化，主要可以表现在以下2个方面.

一是上述提到的数据处理的可视化.除了探究平抛运动的轨迹特点外，利用GeoGebra的多项式拟合功能也能直观探究两个不同物理量间的定量关系，如小车速度随时间变化的规律、自由落体运动的规律、弹簧弹力与形变量的关系等等.后续从拟合函数、图像斜率等进行分析，能深入理解物理规律，还能得到如加速度、劲度系数等物理量的值，让学生体验完整的探究过程，并体会到信息技术的便利及高效.

二是进行模拟仿真实验，主要针对实际教学不好开展或者是实验现象不明显、不直观的实验.例如波的叠加，利用GeoGebra软件的绘图功能动态呈现两列波叠加之后的波形图，甚至探究相关物理量的变化对叠加结果的影响；[9]又如光的干涉，利用GeoGebra软件以波动的形式动态、立体地展示光的传播及干涉过程，使整个场景更加鲜活,加深学生对于光的波动性的理解.[10]