基于投资者不同风险偏好的风险评估与预警体系调查研究

马丽敏

(河北省农林科学院 农业资源环境研究所,河北 石家庄 050051)

随着金融危机爆发，保护投资者合法权益已成为全球金融市场监管的首要问题。因此，对投资者适当性管理是新规则和监管的要求，例如美国的《金融行业监管局规则》的 2111条或欧盟的《金融工具市场指令》。适当性管理包含了财务顾问的义务，即只推荐适合客户个人需求和情况的投资策略，从而避免不当销售。因此，财务顾问需要合理的信息来评估其适用性，例如财务状况、投资目标、投资的时间范围以及客户接受风险的意愿(即风险偏好)。因此，确定适当性在很大程度上取决于评估投资者的能力，尤其是风险偏好问题。有效和可靠地衡量风险偏好是成功进行财务咨询以提高客户满意度的关键因素。

本文目的在于测试一种工具，通过使用真实投资者的样本，将调查数据与真实的投资组合联系起来，从而满足当今的法规要求和科学标准。在本文的分析中，使用来自银行客户数据库的不同投资组合风险度量作为因变量，以测试工具的可靠性和有效性,并进一步分析其与投资者人员统计特征的关系。所获得的结果主要针对投资资本超过2万元的部分咨询客户。研究还包括客户执行，但他们在银行的客户数据库中所占的比例却不足，因此在样本中所占的比例也较低。

一、研究方法

(一)问卷设计

为了选择问卷，本文根据法规要求和科学标准采用了以下6条标准：(1)特别关注兴趣的领域(投资)。(2)衡量风险偏好，不要混淆不同的概念，例如投资目标或风险承受能力。(3)问题和答案选项的措词必须清晰易懂。(4)不应基于数量。排除了基于前景理论问题、赌博任务或彩票选择的问卷。(5)问题不应要求过于具体的投资知识。(6)问卷应在有效性和可靠性方面达到高标准。

(二)受访者

为了评估不同风险偏好并分析其在实际投资组合层面的影响，我们对持有投资组合的某银行的随机样本客户进行调查。问卷是实名的。受试者被告知，他们的答案将与证券公司内部数据相关联，经过梳理之后采用。本文随机抽取了7,963个样本(投资组合中的最低金额为2万元)，并邀请他们参与在线或通过发邮件；1200个客户做出了回应，其中1，194个客户回应有效。

(三)因变量

为了测试问卷的有效性和预测实际投资行为的能力，我们从数据库中提取了3个标准变量，以获得每个受访者其投资所承担的风险。在进行调查的同时对数据进行观察。

1.投资组合中股票百分比

主要使用投资组合中股票的百分比作为因变量。假定股票占总资产的比例高反映了投资者对风险的厌恶程度较低，反之亦然。为了支持我们的结果与其他研究的可比性，本文还研究了风险偏好与客户投资组合中股票比例之间的关系。与其他研究不同的是，因变量是基于实际的投资组合数据。对于包含多资产基金的投资组合(投资于不同资产类别的基金)，使用基金拆分数据来提取正确比例的股票。股票在投资组合中的比例计算如下：设E表示给定的n个工具集合对m个资产类别的矩阵，E=[eij]∈n×m，其中eij∈,i=1，…,n,j=1,…,m并且对所有i有投资组合的权重

关于m个资产类别，有

X=w′E=(x1,…,xm)∈m.

因此，从客户投资组合中属于n种工具的资产类别mstocks的总和可得到投资组合中股票的百分比。

2.投资组合波动性(3年)

为了将投资者的投资组合作为一个整体来考虑，将波动性作为衡量财务风险的一个指标。这里的投资组合波动率是从调查开始3年之内算起的 (月回报率)。投资组合波动性定义为

其中rt=第t个月的客户投资组合收益。

3.整体投资组合风险指标

最后，使用整体投资组合风险指标作为因变量。它基于调查时相关的风险承担分配(与投资组合的波动性相比，反映了三年内承担的风险)。该指标是基于投资者投资组合中的工具分配到8个风险类别中的1个。这些类别的范围从0(低风险)到7(高风险)，每个类别都由一个上下波动边界来定义。将单个工具分配给其中一个类别是基于其长期历史波动性，并通过独立于本研究的投资专家的定性审查进行验证。客户投资组合中的少量投资工具不属于风险类别，因此没有被整体风险指标考虑在内。平均而言，该指标反映了投资组合中93.7%的资产。投资组合整体风险指标的权重为

每种工具的风险分类

是通过整体投资组合风险指标(OPRI)=w′RC得出。

这样的分类符合欧盟金融工具市场法规(MiFID)要求的适当性测试的最佳实践标准。我们的指标是数量加权指标(即投资者投资组合中的每种金融工具均按其百分比份额加权，得出一个单一的分数)。因此，该措施忽略了根据现代投资组合理论的投资组合多元化原则。

二、调查研究

(一)衡量不同风险偏好

对问卷中使用的项目进行了范围和适用性的分析。通过因子分析确定股票投资意愿和不同风险偏好两个维度，并尽可能排除不相关的项目。KMO(Kaiser-Meyer-Olkin)抽样充分性测度(=0.82)和巴特利特球形检验(p< 0.00)证实了项目足以进行因子分析。表1给出了使用主轴分解的最终旋转因子矩阵。

表1 项目的因素和可靠性分析

这两个维度都通过因子分析得到了证实，因子权重得分范围为0.66至0.87。这两个因素解释了总方差70.0%(分别为35.9%和34.2%)。如果使用量表，这两个维度都显示出较高的克伦巴赫α水平，即股票投资意愿为0.87，不同风险偏好为0.86。因此，股票投资意愿和不同风险偏好这两个维度可以分别用3个项目可靠地衡量。因此在Keller和Siegrist[3]的原始不同风险偏好量表中加入该附加项目是正确的，因为它显著提高了原始量表的克伦巴赫α值。

此外，用于比率表的所有项目的失误值都非常低，(只有1.3～1.9%的参与者选择了答案选项“我不知道”)(参见表2)。这表明，对于我们样本中的所有投资者而言，这些项目都是可以理解的，并且似乎不需要深入的金融知识。

表2 所有项目的描述

为了达到设计一种实际使用工具的目的，我们还计算了一个不同风险偏好指数，包括前面提到的两个风险等级。我们假设，股票投资意愿规模不仅反映了作为特定资产类别的股票投资意愿，而且总体上也反映了投资金融市场的意愿。换句话说，这个子量表可以用来衡量金融投资的风险偏好。因此，应该有可能将其与不同风险偏好量表结合起来以形成不同风险偏好指数。为了计算该指标，对不同风险偏好量表的项目进行了重新编码。然后将指数计算为所有6个项目的总和，其中每个比例点都有相应的点数。因此，指数从6点到30点不等。其均值为17.35，标准差为5.33。表3给出了不同风险偏好指数的可靠性分析结果。不同风险偏好指数的克伦巴赫α值为0.88。

表3 不同风险偏好指数的可靠性分析(n=1153)

(二)风险偏好测量的有效性

在确定了衡量投资者风险偏好的可靠量表后，我们计算了回归模型来评估这些测量的有效性。作为客户实际投资组合风险的指标，使用了从银行客户数据库中提取的因变量部分中描述的3个测量值：投资组合中的股票百分比、投资组合波动性(3年)和总体投资组合风险指标。

所有指标均用作回归模型中的因变量，作为实际投资行为的预测指标来评估风险偏好测量的有效性。

回归模型表明，这两个量表与实际投资行为之间存在非常密切的关系。

当以投资组合中的股票比例作为因变量时，股票投资意愿和不同风险偏好这两个预测因子解释了37%的方差(R=0.61，调整后R2=0.37)。股票投资意愿的相对影响(标准β值为0.44)明显高于不同风险偏好的影响(标准β值为0.24)。此外，两个尺度解释了24.0%的客户的投资组合波动性(R=0.49，调整后R2=0.24)。

最后，总体投资组合风险指标模型显示了最佳结果： 可以解释风险指标方差41%(R=0.64，调整后的R2=0.41)。两种量表的标准化β评分均有显著性差异(p < 0.01)。表4中的结果表明，投资股票的意愿对投资组合风险水平的影响要大于不同风险偏好(分别为β=0.46和β=0.26)。这与使用投资组合中的股票百分比作为因变量的回归模型的结果非常相似。

表4 投资组合中的股票百分比，投资组合波动率(3年)和总体投资组合风险指标的回归模型

比较这三个模型，似乎总投资组合风险指标比投资组合中的股票百分比或投资组合波动性更能代表个人风险偏好。使用我们的不同风险偏好指数作为整体投资组合风险的一个预测指标，也会导致该指数与实际承担的风险之间的高相关性 R=0.63，这是通过整体投资组合风险指标来衡量的。风险偏好指数解释了投资组合风险方差40%。

如表5所示，不同风险偏好指数的回归模型得出的结果与表5所示的结果非常相似：投资组合中股票的百分比(R=0.61，调整后的R2=0.37)和投资组合波动性(R=0.49，调整后的R2=0.24)的方差小于整体投资组合风险指标的方差。因此，不同风险偏好指数将作为所有进一步分析的因变量。

表5 以不同风险偏好指数作为实际行为预测指标的回归模型

(三)性别、年龄和财富

人口统计学特征已被广泛用作风险偏好分类的鉴别因素。为了深入了解该量表，我们将调查范围扩展到了风险偏好和人口统计之间的关系(例如，关于性别、年龄和财富)。大多数已发表的与财务决策相关的研究发现，男性的风险偏好要高于女性。此外，不同风险偏好随着年龄的增长而降低。Rolison等人发现，男性的年龄呈二次趋势，女性的呈线性趋势，风险偏好上的性别差异在年轻人中更为明显，并且随着年龄的增长而减小。最后，风险偏好与财富呈正相关。

1.性别差异

男性在不同风险偏好的所有衡量指标上的得分都明显高于女性，在实际投资方面的得分也明显高于女性。如表6所示，男性比女性表现出明显更高的股票投资意愿(M=3.61，SD=1.04，t=-7.03，p≤0.01)，以及较高的风险偏好(M=2.58，SD=0.92，t=-10.44，p≤0.01)和不同风险偏好指数(M=18.57，SD=5.20，t=-9.75，p≤0.01)。看看他们的实际投资行为，可以发现同样的结果：根据从银行内部数据得出的总体投资组合风险指标，男性得分明显更高(M=3.11，SD=1.30，t=-6.40，p≤0.01)，持有的股票明显多于女性(t=-5.67，p≤ 0.01)，他们的投资组合在过去三年中表现出明显更高的波动性(M=6.86%，t=-6.97，p≤0.01)。

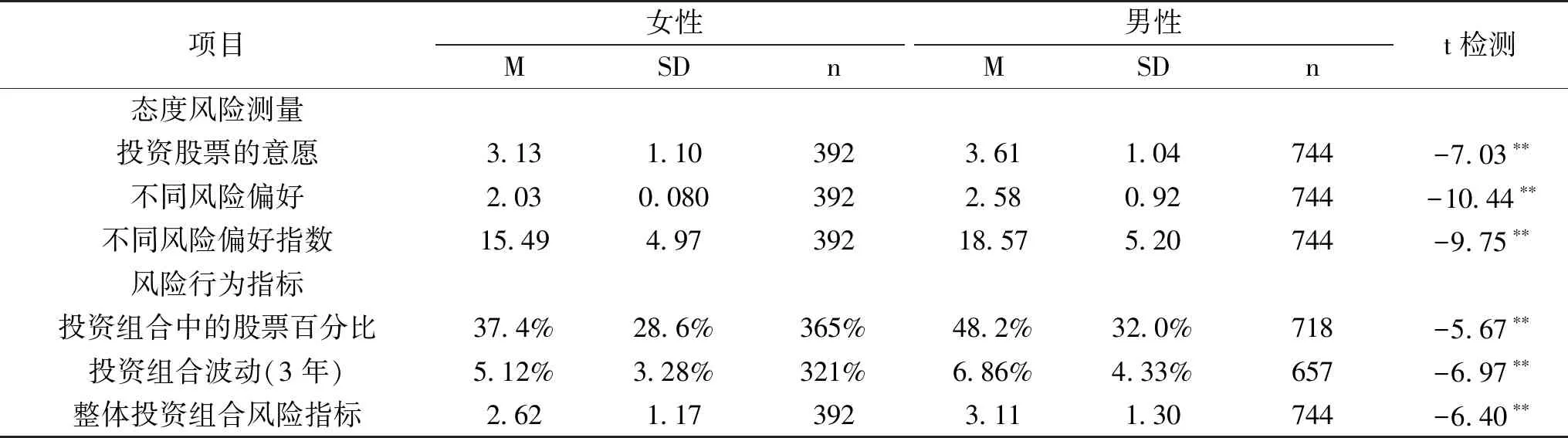
表6 态度风险指标和风险行为方面的性别差异

2.年龄

我们的不同风险偏好指数所反映的风险承担意愿在投资者的生命周期中不断变化。年龄与不同风险偏好指数的相关关系明显呈倒u型，男性在50岁左右达到顶峰，女性在55岁左右达到顶峰(R2=0.02，F=11.82, p≤0.01的二次函数模型相关性略优于R2=0.01，F=17.25, p≤0.01的线性函数)(见表7)。

表7 不同风险偏好指数(因变量)与年龄(因变量)之间的相关性

这一观察结果对男性和女性投资者均适用(见图1)：尽管对于女性而言，线性模型显示年龄与风险偏好之间无显着相关性(R2=0.01，F=2.37，p>0.05)，但二次函数确实存在相关性(R2=0.02，F=3.02，p≤0.05)。对于男性，两种模型都可以使用，但二次函数显示的相关性(R2=0.03，F=10.52，p≤0.01)比线性模型(R2=0.02，F=16.78，p≤0.01)略好。

图1 生命周期中性别和年龄的风险偏好差异

对于男性，这些结果与Rolison等人的发现相一致，但与他们关于女性的研究发现相矛盾，因为女性的线性趋势不显著，而二次函数明显。

3.财富

随着财富的增加(以包括银行中存储的现金在内的资产总额衡量)，承担风险的意愿也随之提高。我们发现风险偏好指数与客户财富之间存在r=0.22(p≤0.01，n=1,153)的适度相关性。从不同的财富值来看，风险偏好指数存在明显差异(见表8)。

表8 按财富值划分的风险偏好差异

为了评估对风险行为的影响，我们在回归模型中逐步引入了人口统计学变量。结果见表9。

表9 以不同风险偏好指数和人口统计变量作为预测整体投资组合风险指标的回归模型(n=1129)

尽管在我们的研究中，男性的投资组合平均风险水平高于女性，但在个人层面上，他们似乎都是根据各自的风险偏好进行投资的。性别作为实际风险承担的额外预测因素没有显著的解释力，也不能解释额外的方差(ΔF=0.18，p>0.05)。年龄也是如此：年龄不考虑回归模型中的其他方差(ΔF=0.09，p>0.05)。因此，不同风险偏好指数似乎已经考虑到了性别和年龄差异。

另一方面，客户的财富可以作为预测指标，显着但仅略微提高了模型的解释能力(ΔF=20.99，p≤0.01)。客户的财富越多，越有可能投资于风险更高的投资组合。财富额外增加了1.0%的方差。

三、讨论

本文对个人意愿及其风险偏好的测算得出以下结论:它表明不同风险偏好可以使用6个项目可靠地测量(不同风险偏好指数的克伦巴赫值=0.88)。这些发现与Weber等人的研究一致，他们表明4-8个项目在可靠性方面是足够的。

此外，我们的结果表明，以投资环境中的风险偏好为重点的可理解的陈述可以用作投资者在金融市场投资时承担的实际风险的有效预测指标。使用财务风险指标，可以解释总投资组合风险的方差40%，存款股票百分比37%和投资组合波动性22%。与风险研究的其他发现相比，我们的指数似乎提供了有效的结果，并解释了实际投资者行为的大量差异。