基于离散单元法的发射装药挤压破碎模拟实验*

张瑞华，芮筱亭，赵宏立，王琼林，靳建伟

（1.西安近代化学研究所，陕西 西安 710065；2.南京理工大学发射动力学研究所，江苏 南京 210094）

随着国防现代化的不断推进，对武器性能提出了大口径、远射程、大威力的发展需求，高能量高安全是弹药发展的永恒主题。目前，形成共识的发射装药引起膛炸的机理为：“低温发射装药-挤压-破碎-增面-增燃-增压-膛炸”，即发射药破碎极易导致膛炸事故[1-2]。因此，如何准确描述相应装药结构下发射装药的挤压破碎过程，成为高能量高安全发射药研究的技术瓶颈问题。

学者们通过试验或数值模拟对发射药及发射装药挤压破碎进行了研究。Gazanas等[3]利用落锤和高速液压伺服装置研究了M30、JA2发射装药的压缩和撞击力学性能，用7.8 mL 小型密闭爆发器测量破碎药粒的燃烧规律，得出破碎药粒的燃面是未破碎药粒的6 倍。陈言坤等[4]综述了用于发射药和发射装药力学性能研究的落锤冲击试验、空气炮试验、分离式霍普金森压杆试验和动态挤压物理仿真试验等，但是对发射装药的破碎模型和仿真还需进一步研究。离散单元法（discrete element method, DEM）是Cundall[5]于1971年分析岩石等散体的力学行为时提出的，已被广泛应用于结构工程、岩土工程、散体力学以及爆炸力学等领域。Jiang 等[6]建立了基于离散单元法的发射装药挤压破碎程序，模拟了发射装药动态破碎过程并给出了三维动画显示；王燕等[7]对不同初始堆积发射装药开展了挤压破碎实验，并运用离散单元法进行了实验验证；以上研究采用弹簧-球单元破碎模型，为发射装药挤压破碎模拟提供了研究手段。弹簧-球模型简化了接触力的计算和程序的编制，但是模型中弹性系数的确定较大程度上依赖于实验值和经验值。EDEM软件在计算颗粒破碎方面精确且高效，具有接触模型参数由材料物性给定（如密度、弹性模量、泊松比等）、对实验值和经验值依赖较少、易于确定等优点。目前采用专业的离散单元法模拟软件如EDEM[8]以及Hertz-Mindlin 黏结接触破碎模型[9]等对发射装药挤压破碎开展的模拟研究较少。

国内外大部分膛炸事故发生于中大口径火炮，其主装药普遍采用花边十九孔发射药，因此，探究花边19孔发射药的动态力学性能对于研究火炮发射装药的发射安全性至关重要。本文中，以硝胺花边十九孔发射药为研究对象，运用EDEM 软件对低温下硝胺发射装药挤压破碎和破碎发射装药密闭爆发器进行模拟，结合硝胺发射装药动态挤压破碎实验和密闭爆发器实验，对比模拟和实验情况下的底部挤压应力、破碎发射装药燃气生成规律和起始动态活度比，实验验证数值模拟系统和参数选取的正确性。

1 发射装药挤压破碎数值模拟系统

1.1 离散单元法

20 世纪90年代以来，各种离散单元法商业软件相继出现，如美国Itasca 公司开发的基于球形的PFC3D软件、英国DEM-Solutions公司开发的商业化三维离散元EDEM 软件等。相比之下，PFC软件主要通过程序语言实现命令，使用较复杂。EDEM 软件中的API 颗粒替换技术[8]对计算冲击破碎更有优势。

API颗粒替换技术中的大颗粒是为了给替换的小颗粒群占据位置和提供中心坐标，替换成功后该颗粒快速离开计算区域；小颗粒群以大颗粒模型的中心坐标为相对位置进行颗粒替换，由若干个同种材料的小球黏结形成需破碎颗粒的形状，并在指定时刻形成黏结键，该颗粒具备2种接触模型：Hertz-Mindlin无滑动接触模型以及Hertz-Mindlin 黏结接触模型，通过小球之间的黏接键断裂来表征物料的破碎。

在发射装药挤压破碎模拟过程中，如果离散颗粒太大，将难以表征真实发射药破碎的小颗粒，若离散颗粒太小，则计算耗时过长。因此本文中将花边十九孔发射药离散为由95颗直径相同的小球颗粒组成的离散单元模型，小球颗粒半径为1.1 mm，输出其坐标作为API 颗粒替换技术中的小颗粒模型，替换前后的颗粒以及黏结模型如图1所示，共形成286个黏结键。

图1 发射药颗粒替换黏结过程Fig.1 Replacement and forming bond process of propellant particle

1.1.1 Hertz-Mindlin 无滑动接触模型

E D E M 软件中默认使用的接触模型为Hertz-Mindlin 无滑动接触模型，如图2所示，该模型用于颗粒与颗粒之间、颗粒与装置之间的接触力计算，在颗粒计算方面精确且高效。

图2 Hertz-Mindlin 无滑动接触模型Fig.2 Hertz-Mindlin non-sliding contact model

法向力Fn为法向弹性力Fne和法向阻尼力Fnd之和；切向力Fτ为切向弹性力Fτe和切向阻尼力Fτd之和；库伦摩擦fsFn限制切向力，其中fs为静摩擦因数。具体表达式分别为：

其中：

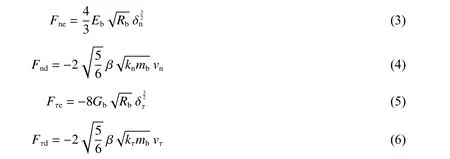
式中：δn、δτ分别为法向和切向重叠量，vn、vτ分别为相对速度的法向和切向分量，kn、kτ分别为法向和切向刚度，β 为恢复系数e的表达式，Eb、Gb、Rb、mb分别为等效杨氏模量、等效剪切模量、等效半径、等效质量。具体表达式为：

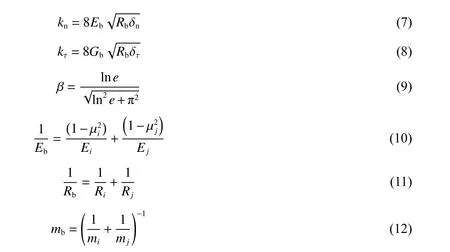
式中：Ei、Ej分别为颗粒i和颗粒j的杨氏模量，µi、µj分别为颗粒i和颗粒j的泊松比，Ri、Rj分别为颗粒i和颗粒j的接触球体半径。

通过在接触表面施加一个力矩来计算非常重要的滚动摩擦，表达式为：

式中：fr为滚动摩擦因数，Rt为接触点到质心的距离，ωt为物体在接触点处的单位角速度矢量。

1.1.2 Hertz-Mindlin 黏结接触模型

Hertz-Mindlin 黏结接触模型如图3所示。Hertz-Mindlin 黏结接触模型运用一个有限大的“胶粘剂”黏结在接触范围内的颗粒，该黏结键可承受切向和法向位移，传递黏结颗粒之间的力和力矩，直到黏结键承受的应力达到最大的临界切向和法向应力，即黏结键断裂点，此后颗粒作为硬球互相接触作用[9]。这个模型基于Potyondy等[9]的工作，特别适用于模拟混凝土和岩石结构。该模型无法描述发射药破碎后局部能量聚集、热点形成过程。

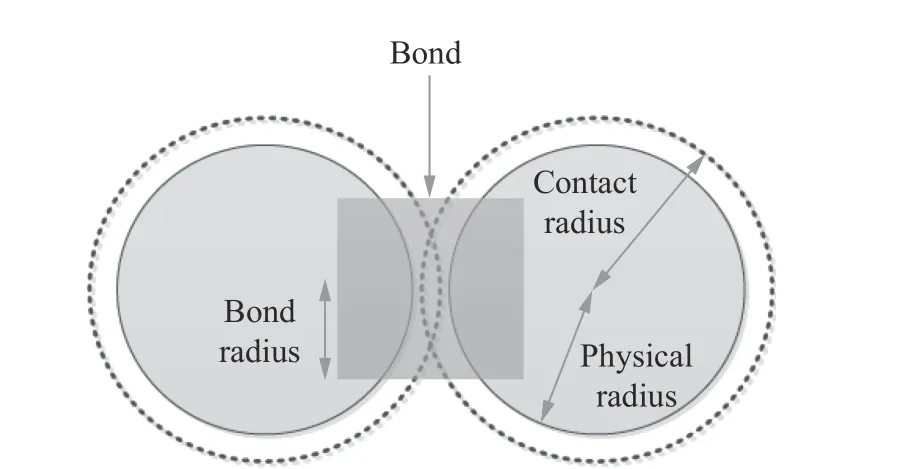
图3 Hertz-Mindlin 黏结接触模型Fig.3 Hertz-Mindlin bonding contact model

颗粒在黏结生成时间tbond黏结在一起。黏结以后，颗粒上的黏结力F¯n、F¯t和力矩M¯n、M¯t设置为零，并在每个时间步通过下式逐步调整：

其中：

式中：Rbond为黏结半径，S¯n、S¯τ分别为法向和切向黏结刚度（单位面积上的法向和切向刚度，单位为N/m3），Δt为时间步长，vn、vτ分别为颗粒法向和切向速度，ωn、ωτ分别为颗粒法向和切向角速度。

当法向和切向剪切应力超过某临界值时，黏结键断裂。定义法向应力和切向应力的最大值如下：

以上黏结力、黏结力矩是另外加到Hertz-Mindlin 无滑动接触力中的。该模型只能用于颗粒与颗粒之间，且可以在颗粒没有实际接触时起作用，因此接触半径的设置应大于实际半径。

Hertz-Mindlin 黏结接触模型中参数的计算公式如下[9]：

式中：E¯b为黏结键弹性模量；Sn/Sτ为法向刚度与切向刚度的比值，与泊松比相关。

1.2 建立发射装药挤压破碎数值模拟系统

1.2.1建立发射装药挤压破碎力学模型

应用EDEM 软件，首先生成69个大球颗粒，在重力作用下进行自然堆积，堆积稳定后进行API颗粒替换，颗粒替换的同时形成黏结键，替换后的发射装药模型进一步进行自然堆积，当发射药颗粒不再运动时，则认为发射装药堆积密实。堆积密实的发射装药离散单元力学模型如图4所示，将图5的燃烧室压力曲线作为冲击载荷加载到图4中的上盖板，进行发射装药挤压破碎数值模拟。

图4 发射装药离散单元力学模型Fig.4 Discrete element mechanical model of propellant charge

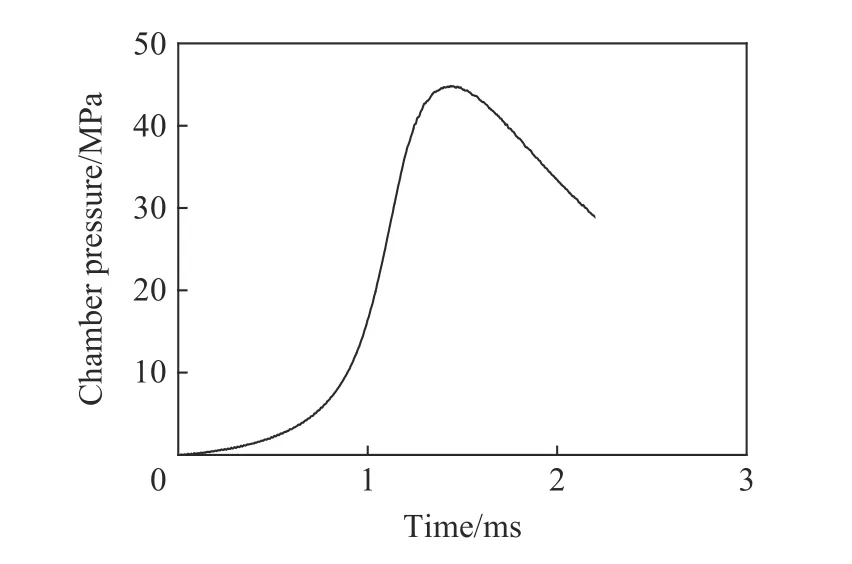
图5 上盖板压力时间曲线Fig.5 Pressure-timecurve of upper cover plate

1.2.2数值模拟参数选取

对保温到低温（–40℃）下的单颗硝胺发射药进行落锤冲击试验，试验前将发射药粒加工成轴向均匀、两端面垂直轴向的试样，试验获得的弹性模量为899.1 MPa、压缩强度为98.5 MPa。

对图1所示的单颗发射药离散单元模型进行落锤冲击模拟，模拟边界条件均与实验相同，目的是寻找合适的Hertz-Mindlin黏结接触模型参数，使得单颗发射药落锤冲击模拟结果与单颗发射药落锤冲击试验结果符合较好[10]。依据Potyondy等[9]提出的黏结模型参数选取原则，令黏结键弹性模量E¯b与实验获得的发射药粒弹性模量相同，（Sn/Sτ）与泊松比相关，选取的黏结半径为1 mm。则由式(22)、式(23)计算得到低温下黏结模型的法向黏结刚度和切向黏结刚度，令其保持不变；法向临界应力和切向临界应力的比值也与泊松比有关，改变法向临界应力σc和切向临界应力τc的值，以符合最合适的黏结接触模型参数，使得发射药颗粒输出的压缩强度与落锤实验获得的一致。本文中选取6组Hertz-Mindlin黏结接触模型参数，分别进行单颗发射药落锤冲击模拟。

模拟参数和获得的最大应力如表1所示，其中序号4模拟获得的最大应力98.24 MPa与落锤冲击试验获得的压缩强度98.5 MPa最接近，选择序号4的一组参数作为低温下参数符合结果，用于进一步进行发射装药挤压破碎数值模拟。发射药颗粒的泊松比µ=0.3[11]，密度与真实发射药密度1 650 kg/m3相同。

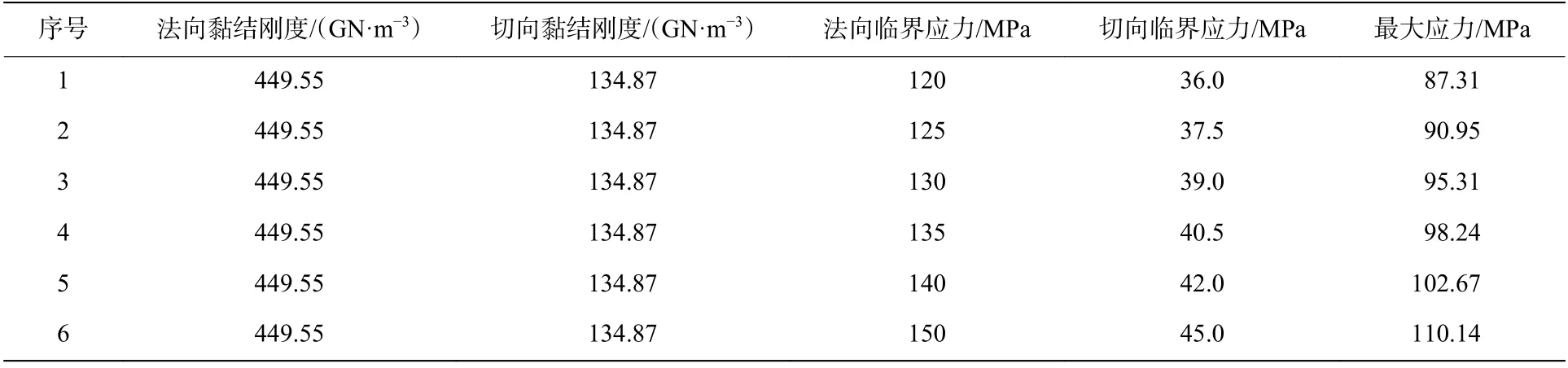
表1 数值模拟参数与结果Table 1 Model parameters and simulation results

2 发射装药挤压破碎模拟实验验证

2.1 发射装药动态挤压破碎实验

发射装药动态挤压破碎实验装置[2]如图6所示。实验原理为：在燃烧室中加入点火药，燃烧生成高压气体推动活塞向下运动，高速运动的活塞冲击模拟药室中的发射装药试样，用以模拟火炮发射过程中弹底发射装药的挤压破碎过程以及发射药床受到的挤压应力，PVDF应力传感器[12]测试发射装药底部挤压应力时间历程。取图7所示的69颗硝胺花边十九孔发射装药为研究对象，实验前将发射装药保温到–40℃，对相同质量的发射装药分别开展不同燃烧室压力下的发射装药动态挤压破碎实验。

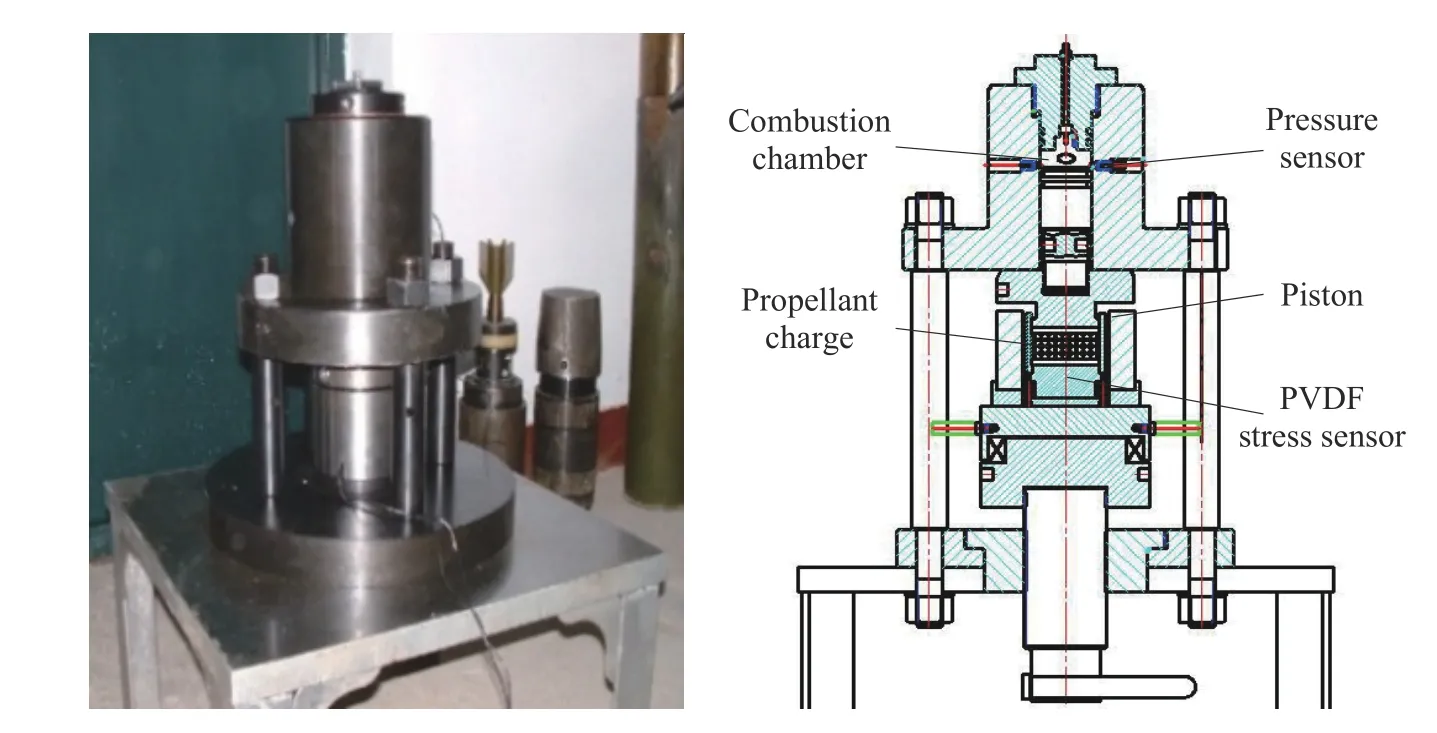
图6 发射装药动态挤压破碎实验装置及原理图Fig.6 Experiment deviceand schematic diagram of the dynamic compression and fracture of propellant charge

图7 实验发射装药Fig.7 Experiment propellant charge

发射装药动态挤压破碎实验条件和结果如表2所示，实验获得的3发破碎发射装药如图8所示，可以看出：在第2发和第3发实验中发射装药出现了粉末状破碎，燃烧时极易引起压力异常现象；且在第3发实验中几乎每颗发射药粒都发生了破碎，破碎形状各异、大小不一。

表2 实验条件和结果Table2 Experiment conditionsand results

图8 低温下实验获得的破碎发射装药Fig.8 Fracture propellant charge obtained by experimentsat low temperature

2.2 发射装药挤压破碎模拟结果

在图4所示的发射装药离散单元力学模型的上盖板分别加载图8中对应实验的燃烧室压力，分别进行发射装药挤压破碎模拟。模拟结果如表3所示，模拟获得的3发破碎发射装药离散单元模型和黏结键模型分别如图9、图10所示。随着模拟的进行，发射装药发生破碎，发射药粒破碎形状各不相同，但是模拟发射装药的体积总量没有发生改变，通过统计模拟结束时刻的总体黏结键断裂情况来描述发射装药破碎程度。发射装药初始黏结键个数为286×69=19 734，3 发模拟黏结键断裂比例分别达到6%、23%、38%，加载的燃烧室压力越大，模拟结束时发射装药黏结键连接个数越少、挤压应力峰值越大，发射装药破碎越严重，与实验现象一致。

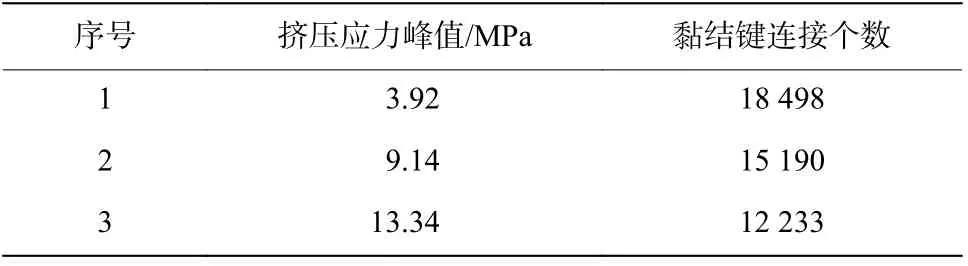
表3 数值模拟结果Table 3 Simulation results

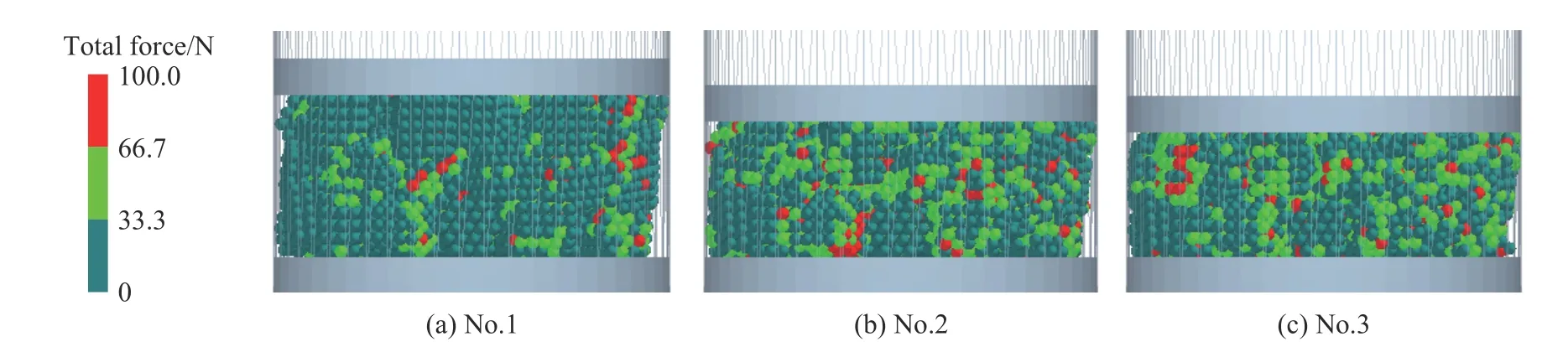
图9 采用离散单元法模型获得的挤压破碎模拟结果Fig.9 Compression and fracture simulation results with thediscrete element model

图10 采用黏结键模型得到的挤压破碎模拟结果Fig.10 Compression and fracture simulation resultswith the bond model

2.3 发射装药挤压应力实验验证

不同燃烧室压力下模拟与实验获得的发射装药底部挤压应力对比曲线如图11所示。由图11可知，加载的燃烧室压力越大，挤压应力曲线脉宽越窄，曲线到达峰值前的上升速度越快；数值模拟与实验获得的挤压应力时间对比曲线存在少许误差，这是由于发射药的离散单元数值模拟模型不具有小孔，与真实花边十九孔发射药存在差异；且实验与数值模拟的发射装药都是随机堆积的，存在随机误差。在加载相同燃烧室压力下，模拟与实验获得的底部挤压应力时间曲线总体吻合较好，但模拟与实验获得的破碎发射装药的破碎程度和燃气生成规律需进一步验证。

3 破碎发射装药燃气生成规律实验验证

运用密闭爆发器实验系统对图8中的3发破碎发射装药分别进行起始动态活度比实验，测试获得相应破碎发射装药的燃气生成规律，依据起始动态活度比理论[1]处理得到起始动态活度比R0。起始动态活度比等于相同压力下破碎发射装药与原未破碎发射装药被点燃时刻的面积比，即表征发射装药的破碎程度。将图9所示的3发破碎发射装药分别进行密闭爆发器实验模拟，运用基于离散单元法的破碎发射药燃烧函数[13]模拟获得破碎发射装药的燃气生成规律及起始动态活度比。

数值模拟与实验获得的破碎发射装药密闭爆发器压力时间对比曲线如图12所示，起始动态活度比如表4所示。可以看出，对应的压力时间曲线吻合较好，起始动态活度比误差最大值为6.05%，误差较小。这说明建立的发射装药挤压破碎模型和拟合研究获得的黏结接触模型参数具有较好的适用性。同时发现，第2发和第3发破碎后的压力时间曲线前半段实验的燃气生成规律大于数值模拟，而后半段则相反，且破碎程度越严重，曲线差别越大。这是由于数值模拟获得的破碎发射装药的最小颗粒半径大于实验获得的粉末状破碎发射药，这些细小的粉末会导致密闭爆发器实验初始阶段燃气生成量较大，实验获得的发射装药破碎程度越严重，细小的粉末越多，实验与模拟获得的压力时间曲线误差越大。当实验获得的细小粉末燃烧完后，剩下的大块实验破碎发射装药的燃烧面积将小于模拟获得的破碎发射装药，因而实验的燃气生成规律后半段曲线小于数值模拟。当R0<2.0时[2]，压力时间曲线吻合较好，说明本文的离散元小球颗粒半径满足计算要求。

表4 数值模拟与实验起始动态活度比对比Table 4 Comparision of initial dynamic vivacity ratios in simulation and experiment

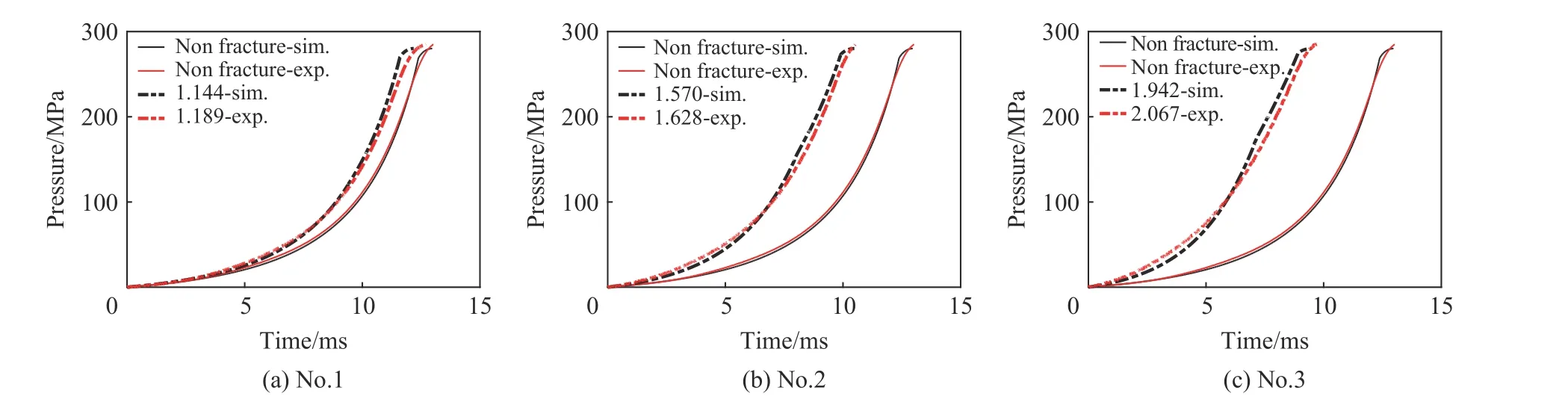
图12 密闭爆发器数值模拟与实验压力时间对比曲线Fig.12 Comparison of simulated and experiment pressure-time curves in the closed bomb

4 结 论

（1）加载不同燃烧室压力下发射装药挤压破碎模拟获得的黏结键断裂比例分别达到6%、23%、38%，与发射装药动态挤压破碎实验现象定性一致，且模拟与实验获得的底部挤压应力时间曲线总体吻合较好。

（2）在不同破碎程度的发射装药密闭爆发器模拟与实验中，对应破碎发射装药的压力时间曲线吻合较好，起始动态活度比误差最大值为6.05%，误差较小，验证了破碎发射装药燃烧规律的一致性。当数值模拟破碎发射装药的起始动态活度比R0<2.0时，离散元小球颗粒半径满足计算要求。

（3）对比实验和数值模拟情况下的底部挤压应力、破碎发射装药燃气生成规律和起始动态活度比，实验验证了数值模拟系统的正确性和黏结接触模型参数拟合的合理性，研究结果为再现由发射装药破碎导致的膛压异常奠定了理论和模拟基础。