有限元模拟分析金属切削加工

陆芳

编者按：在这篇文章中，作者采用有限元法模拟分析金属切削加工过程，建立金属切削加工有限元模型，研究分析切削速度、背吃刀量、进给量对切削力的影响，并通过研究优化切削加工工艺。

前言

有限元法模拟切削加工主要集中在模拟分析切削参数对已加工表面残余应力、切削力以及切削温度刀具磨损等方面的影响，从而优化切削参数，同时也分析模拟切屑形状以及形成的过程。孔虎星等[1]主要建立钛合金的切削有限元模型，分析了切削温度、表面应力、切削力分布情况，优化加工工艺。芮执元等[2]主要研究不同切削参数条件下切削力的情况，分析切削速度、进给量、背吃刀量对切削力的影响情况。Hongtao Ding等[3]将有限元应用于模拟分析难加工材料的磨削加工，模拟切屑的形成同时分析温度对刀具磨损的影响。本文综合有限元模拟金属切削加工的优势，用有限元模拟切削加工过程，分析各切削参数对切削力的影响，从而优化切削工艺。

有限元分析

材料本构模型

确定材料的本构模型是有限元分析中至关重要的因素之一。以往研究表明材料的应变受应变率以及温度的双重影响，应变率高则在应变值一定的情况下应力就大，而温度高则材料一定程度上软化，导致应力小，而温度越高，材料的过应力会更加明显[4]，因此精确确定材料的本构模型是个至关重要的难题。对于已经确定的材料的本构模型大致可以分成以下两种：一种就是经验本构模型;另一类为基于物理学的本构模型。本研究采用经验本构Johnson-cook模型，因为这种模型不仅能够反映材料的应变率强化作用，而且还可以反映温升软化作用效果，同时还能反映出材料加工硬化作用，这种本构模型也大量地应用于金属加工的有限元模拟分析中。

Johnson-cook模型如下式所示：

刀—屑接触与摩擦有限元模拟模型的确定

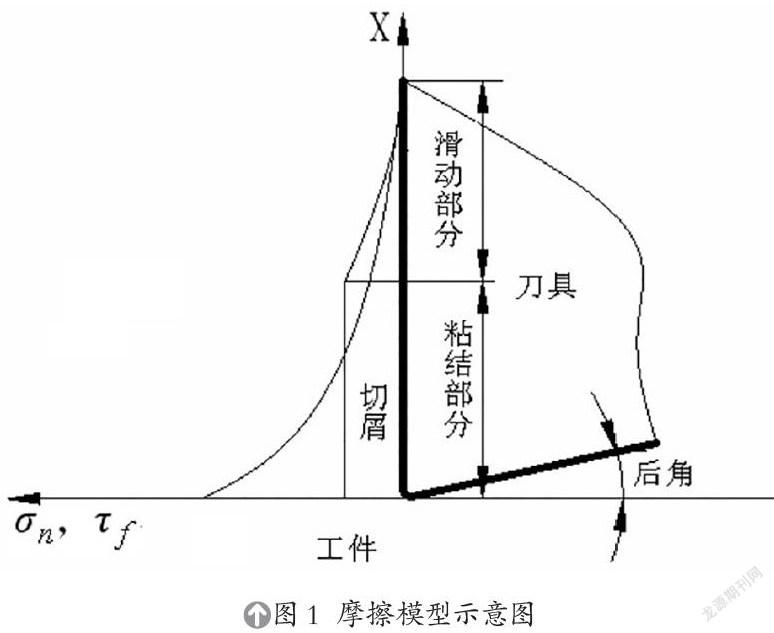
在金属切削加工中，切屑对刀具前刀面的摩擦以及工件对刀具后刀面的摩擦对刀具的使用寿命以及加工的质量有决定性的作用。切屑的形成过程是：刀具对切削层的挤压以及摩擦作用，在第一变形区内变形层沿刀具的前刀面流动，然后前刀面的压力及摩擦作用使得切屑层的变形更为严重，形成了第二变形区位于刀具的后刀面处，在第二变形区内切屑变形更为严重因摩擦产生的热量也很高，从而导致切屑-刀具接触区域温度很高，对第一变形区的应力应变也会产生一定的影响。如何准确地定义刀-屑之间的接触与摩擦是有限元模拟是否准确的关键。根据刀屑接触区域剪应力的大小将刀屑接触区域分为粘结区以及滑动区，刀屑未完全分离区域段定为粘结区，完全分离的区域段则为滑动区。Zorev[5]加入考虑剪切应力的基础上，建立了包括剪应力在内的应力模型，如图1所示。

切屑分离准则

金属切削加工中，工件被刀具切削分为切屑层以及已加工表面层，切屑层沿着刀具的前刀面流出，本文的有限元模拟切屑分离准则使用的是剪切失效模型准则。对于切屑分离准则[6]主要有两种：一种是物理分离准则，即切屑的分离与材料的物理参数有联系，當材料的某些物理参数如等效塑性应变、应变能密度、应力等[7-8]这些参数到达相应的临界值时材料就分离;另一种则是几何分离准则，该准则采用的依据是所分析物体的几何尺寸变化情况，比如工件相应节点与刀尖节点之间的距离，这个分离准则更准确的描述即为在刀尖加工途径上，刀尖距离与其最近的工件上节点之间的长度不大于一定值时，这个定值是设定的，切屑就脱离基体沿前刀面流出[9]。几何分离准则相对于物理分离准则会比较容易判定，但是节点之间的距离的计算结果有时候难以收敛，而且需要建立一条切屑与工件相分离的分离线。此次研究的有限元模拟切屑分离准则使用的是剪切失效模型准则。

热传导分析

金属加工过程会产生很多热量，尤其是在切削加工硬质合金的过程中。因此，在用有限元分析切削加工时采用的都是热力耦合模型。有限元模拟中切削模拟的传热的能量方程如下：

二维有限元模型建立

本文所用的有限元模拟软件为ABAQUS，对Sialon陶瓷刀具切削加工GH4169镍基高温合金进行二维的模拟仿真。有限元模拟方案为单因素模拟，主要是分析背吃刀量、切削速度、进给量对于刀具切削力的影响。

如图2所示为刀具工件的有限元模拟模型，模型中工件几何尺寸为3mm× 1mm，工件采用均匀划分网格的方式，网格为四节点平面应变热力耦合单元;切屑分为两层分别划分网格，一层为切屑也采用四节点热力耦合单元网格均匀划分，一层为分离层，网格类型与切屑一致。而刀具在网格划分时，刀具距离刀尖位置网格划分较密，网格单元采用四节点热力耦合单元，模拟的初始温度为300K。切削运动的实现是通过给刀具施加一定的速度于刀具网格，速度的方向为沿X轴负方向。预应力的加载是通过固定工件的右边X方向的位移，将一定大小的预拉应力加载至工件的左边界节点上，背吃刀量的不同则是通过采用改变切屑层的厚度来实现的。

切削过程仿真

在本文中关于有限元模拟切削加工过程分析可主要研究三方面内容：等效塑性应变PEEQ，切削温度以及Mises应力。以下即是对这几方面模拟过程及结果的分析。

PEEQ等效塑性应变分布

将刀具的整个加工流程分成四个阶段，约束阶段即将各部件进行约束加载，但还没进行切削的阶段，此时PEEQ值均为零;将刀具开始切入工件时定义为初始切削阶段，当进入这个阶段时，加工层初始成为切屑，是因为加工层受到了刀具的挤压以及剪切作用，使加工层逐渐变成切屑沿剪切面流动，这个阶段的切屑上的PEEQ值最大;当切削进行一段距离或时间后，切削力较为平稳，将这个阶段定义为稳定切削阶段，这个阶段会形成较为稳定的剪切滑移带，这个阶段PEEQ出现最大值，最大值出现在切屑表面上;当切削过程结束时将此阶段定义为切削完成阶段，此时刀具已经脱离工件，已加工表面出现。

切削溫度分布情况

对于切削加工来讲，切削温度是影响其切削加工质量的一个至关紧要的因素，因此，在本文研究模拟切削加工必然会加入温度场的分析。在此模拟中，刀具以及工件的原始温度均设定成300K;到刀具开始切入工件，切削温度在刀具与工件的挤压以及摩擦作用下上升得非常快;当进入稳定切削过程，切屑的流动，刀具与切屑间的摩擦以及刀具后刀面与已加工表面的摩擦，刀具与工件的挤压使得切削温度继续上升，刀屑接触面即前刀面上接近刀尖的区域切削温度达到最大值;在最后切削加工完成阶段，最终的切削段直接被刀具推挤掉，因此大大降低了刀具与切屑之间的磨损，从而降低了切削温度。

Mises应力分布

关于Mises应力分布情况同样也可将其分为四个阶段来进行分析，刀具切削过程可以由以下四阶段组成：（1）刀具即将但还未接触工件，即初始约束阶段，Mises应力大小是零;（2）刀具开始切入工件，即初始切入阶段，此时工件材料初始切离;（3）跟以上两个稳定切削阶段的定义一样，稳定切削阶段切屑与工件产生分离，并且沿刀具的前刀面流动，因为已加工表面对刀具后刀面的相互作用力使得刀具后刀面上接近刀尖处所受应力最大，而Mises应力最大值出现在工件的剪切区中间位置;（4）刀具脱离工件，切削完成，即完成切削阶段。

切削模拟结果的分析

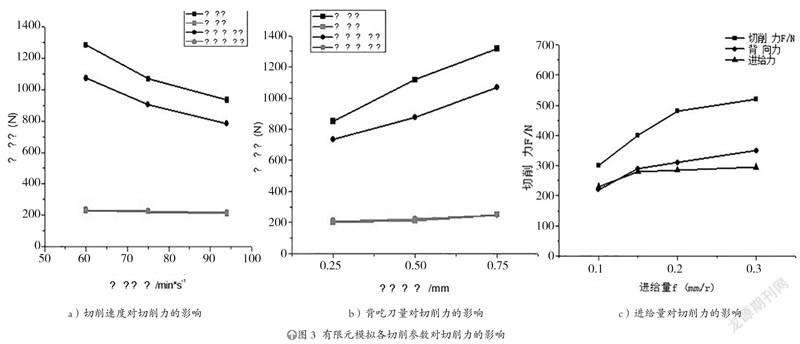
图3（a）所示为切削速度对各切削力的影响情况，指定范围内加大切削速度有利于减小切削过程中的切削力，这主要是由于当切削速度在指定大小内时，速度增大会减小刀具前刀面的磨损，加大剪切角从而导致减小了切屑的变形，切削过程所受的切削力也相应变小。图3（b）所示为不同背吃刀量条件下对各切削力的结果值，随着背吃刀量的增加切削力上升较快，而且综合对比背吃刀量对切削力的影响最大。图3（c）所示为不同进给量条件下对各切削力的结果值，随着进给量的增加切削力上升较快。从关系图中可以看出，对切削力的大小的影响，背吃刀量排第一，切速以及进给量次之。因此，通过模拟可以得出，切削加工若想降低切削力则应采取的切削方案是较大的切速、较小的进给量及背吃刀量。

参考文献：

[1]孔虎星，郭拉凤，尹晓霞.基于ABAQUS的钛合金切削有限元分析[J].机电技术，2011，34（04）：22-23，30.

[2]芮执元，李川平，郭俊锋，等.基于Abaqus/explicit的钛合金高速切削切削力模拟研究[J].机械与电子，2011（04）：23-26.

[3]Ding H，Shen N，Shin Y C.Thermal and mechanical modeling analysis of laser-assisted micro-milling of difficult-to-machine alloys[J].Journal of Materials Processing Technology，2012，212（3）：601-613.

[4]Shih A，Yang H T Y.Experimental and finite element model for rate dependent metal forming processes[J].International Journal for Numerical Methods in Engineering，1991：345-367.

[5]Mosnier C，Agabriel J，Lherm M，et al.International Research in Production Engineering[J].American Society of Mechanical Engineers，1963：42.

[6]Behrens A，Westhoff B.Finite element modeling of high speed machining processes[C].The 2nd International German and French Conference on High Speed Machining，Darmstade，1999.

[7]Iwata K，Osakada K，Terasaka Y.Process modeling of orthogonal cutting by the rigidplastic finite element method[J].Journal of Engineering Materials and Technology，1999：132-138.

[8]Lin Z C，Lin Y Y. A study of an oblique cutting model[J].Journal of Materials Processing Technology，1999，86（1-3）：119-130.

[9]Li K，Gao X L，Sutherland J W. Finite element simulation of the orthogonal metal cutting process for qualitative understanding of the effects of crater wear on the chip formation process[J].Journal of Materials Processing Technology，2002，127（03）：309-324.