算法练习——寻找神秘钥匙

陈新龙

究竟什么是“算法”？“算法”有什么用处呢？算法是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法解决问题的策略机制。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度和时间复杂度来衡量。比如穷举法（1-1000）依次递增循环，能够保证准确率，但是时间上会比较浪费。所以好的算法能够帮助我们更快地解决问题。

寻找神秘钥匙：你说出一个数字n，请根据这个数字n找出一个数k（神秘钥匙），数k必须满足四个要求：一、数字k必须是一个奇数;二、数字k能够被5整除;三、数字k所有因数和为n;四、k小于1000。例如当我们输入数字48后，输出的神秘钥匙就是35，因为35是一个奇数，还能够被5整除，并且小于1000，35的因数为1，5，7，35，四个数字相加等于48。

题目分析：在解决问题前一定要整理思路，题目中提到了两个数n和神秘钥匙k，n是用户输入，k需要满足四个条件：一是可被5整除，那么可以得出k数字的尾数是0或者是5。二是一个奇数，前两个条件合并，k的末位只能是5;在程序中可按5，15，25，35，45递增，以5为基础每次递增10，根据条件四上限是1000。最重要的条件三是所有的因数和为n，所以只需要通过穷举法，依次计算5，15，25，35的因数和，当因数和等于输入数字n时就找到了k（如图1）。

添加两个变量“因数和”“k”“i”。设置“因数和”的初始值0，k的初始值5。询问用户输入一个整数。重复执行直到用户输入的数等于“因数和”或者k>1000。在循环中将k的值每次增加10保证k是奇数和5的倍数（如图2）。

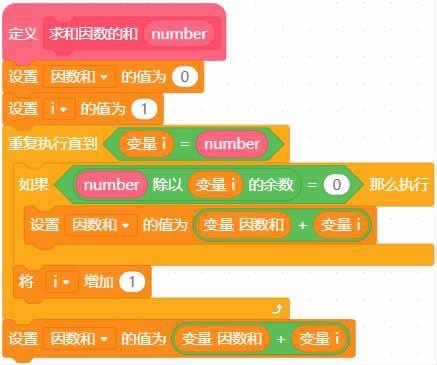
新建积木“求和因数的和k”（自制积木添加输入选项），重复执行到变量i等于数字number（number相当于本次循环的k）。在循环中添加判断如果number除以变量i的余数等于0，能整除说明i为k的一个因數;将其累加入“因素和”;在结尾之处不要忘记数字本身也是一个因数，要把本身也添加到“因素和”里面（如图3）。

当某个数字满足以上的条件的时候，会输出到舞台，如果没有找到钥匙则提示没找到钥匙。