将超表面融入大学物理课堂教学的探索

翟世龙，冀若楠，侯泉文，尹剑波，庞述先

(西北工业大学 物理科学与技术学院，陕西 西安 710129)

在国家大力推行新工科建设的时代背景下，各高校本科基础教学迫切面临着传统模式的深化改革。随着科学研究的不断创新发展，新理念、新方法、新技术不断涌现，因此探索将前沿的科技成果融入教学中，是实现教学改革、推动新工科建设的一种直接且有效的方法[1-3]。

大学物理作为我国工科院校中普遍开设的一门低年级公共课，为学生后续学习其他学科专业课程打下了坚实的理论基础，并且在培养学生科学素养和原始创新能力方面具有重要意义。但是，传统大学物理教学仍然以经典物理为主要内容，往往忽视了经典理论与学科前沿的联系，从而导致教学与科研出现脱节，使学生对大学物理教学产生内容陈旧的不良印象。实际上，随着科学研究的不断深入和人类对科学认知的不断提升，我们所熟知的知识体系往往并不是一成不变的，前人总结出的科学论断在当今或未来社会并不一定能够继续完全成立。若能将前沿的科学研究融入大学物理教学当中，那么学生将会对大学物理的学习产生浓厚的兴趣，从而提高自身的科学素养和创新意识。笔者近年来一直从事超构材料的研究。超构材料是通过将人工功能基元进行空间有序排列而筑成的一类新材料[4]。其核心思想在于利用具有亚波长微结构的重构常规材料来实现天然材料所不具备的反常效应，其中最具鲜明特色的当属反常反射和折射。该理论于1968年由苏联理论物理学家Veselago提出[5]，最早实现于微波领域。随着研究的不断深入，其相关研究范畴迅速扩大，目前已经涵盖了光学、声学、热学、力学等诸多领域，同时催生出了种类繁多的新奇效应，诸如波的定向发射、高效吸波、隐身等[6]。因此，超构材料被普遍认为能够对未来功能器件的构型产生颠覆性影响。正是由于其具有非凡的发展潜力和卓越的应用前景，美国《科学》杂志曾多次将其列入年度十项重要科学进展之一。本文希望以超构材料中的一个重要分支——超表面——的反常反射和折射作为引玉之砖，尝试将前沿的科研成果融入课堂教学，扭转学生对大学物理课程内容陈旧的不良印象，激发学生的批判意识和原始创新能力。

1 费马原理与反射、折射定律

在大学物理课程中，我们学到了费马原理，该原理指出波总是沿着行程或所需时间为极值的路径传播，一般情况下为极小值，因此又被称为“最短时间原理”。根据这一原理，结合数学中的微分知识，我们就可以推导出波在不同介质界面处的反射和折射定律。

设折射率分别为n1和n2的两种介质(介质1和介质2)分别处在X轴的上下两侧，如图1所示。若波从介质1中的A点出发，经过两介质界面上的B点反射后传播至C点，则波传播的总行程S1应为AB和BC的行程之和。设A、B和C三点的坐标分别为(xA,yA)、(x,0)和(xC,yC)，则总行程为

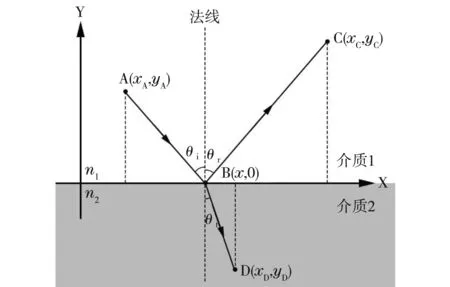
图1 各向同性均匀介质界面处的反射、折射原理示意图

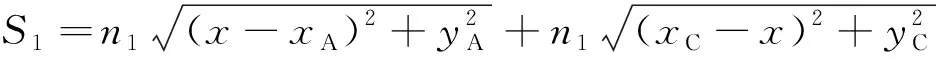
(1)

根据费马原理，必须使S1取极值，因此将S1对x求导并取其导数为0，即可求出B点所在的位置。公式如下：

=0

(2)

此处，若设入射角和反射角分别为θi和θr，则公式(2)可变换为：

sinθi=sinθr

(3)

即反射角等于入射角，公式(3)为波的反射定律。

若波从介质1中的A点出发，经过B点后传播至介质2中的D点(其坐标为(xD,yD))，则波传播的总行程S2应为

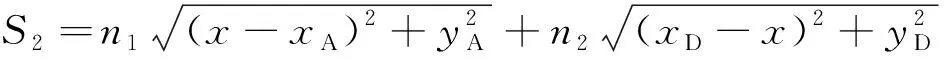
(4)

将S2对x求导并取其导数为0：

=0

(5)

此处，若设折射角为θt，则公式(5)可变换为：

n1sinθi=n2sinθt

(6)

公式(6)为折射定律。

根据反射和折射定律，学生们可以总结出如下规律：入射波和反射波一定会处在法线的两侧，且反射角等于入射角；入射波和折射波也一定处在法线的两侧，且折射角由入射角和两介质的折射率共同决定。需要指出的是，以上规律成立的前提是介质1和介质2必须是各向同性的均匀介质，即界面上的每个点对入射波的响应都是完全一致的。但是，如果在界面处人为铺设一层非常薄的人工材料，且该材料上的每个点对入射波的响应均不相同，那么界面对入射波的反射和折射规律将会发生颠覆性的变化。由于这种人工材料的厚度通常只有入射波长的几分之一至几十分之一，可以近似认为其厚度远小于波长，因此又被称为超表面。

2 超表面的反常反射、折射定律

超表面由特殊设计的不同人工功能基元在空间上有序排列而成，它能使波入射到表面之后，形成的反射波或折射波有一个额外的相位延迟，而且这个相位延迟量φ与位置x有关，如图2所示。下面我们根据费马原理重新推导超表面的反射和折射定律。

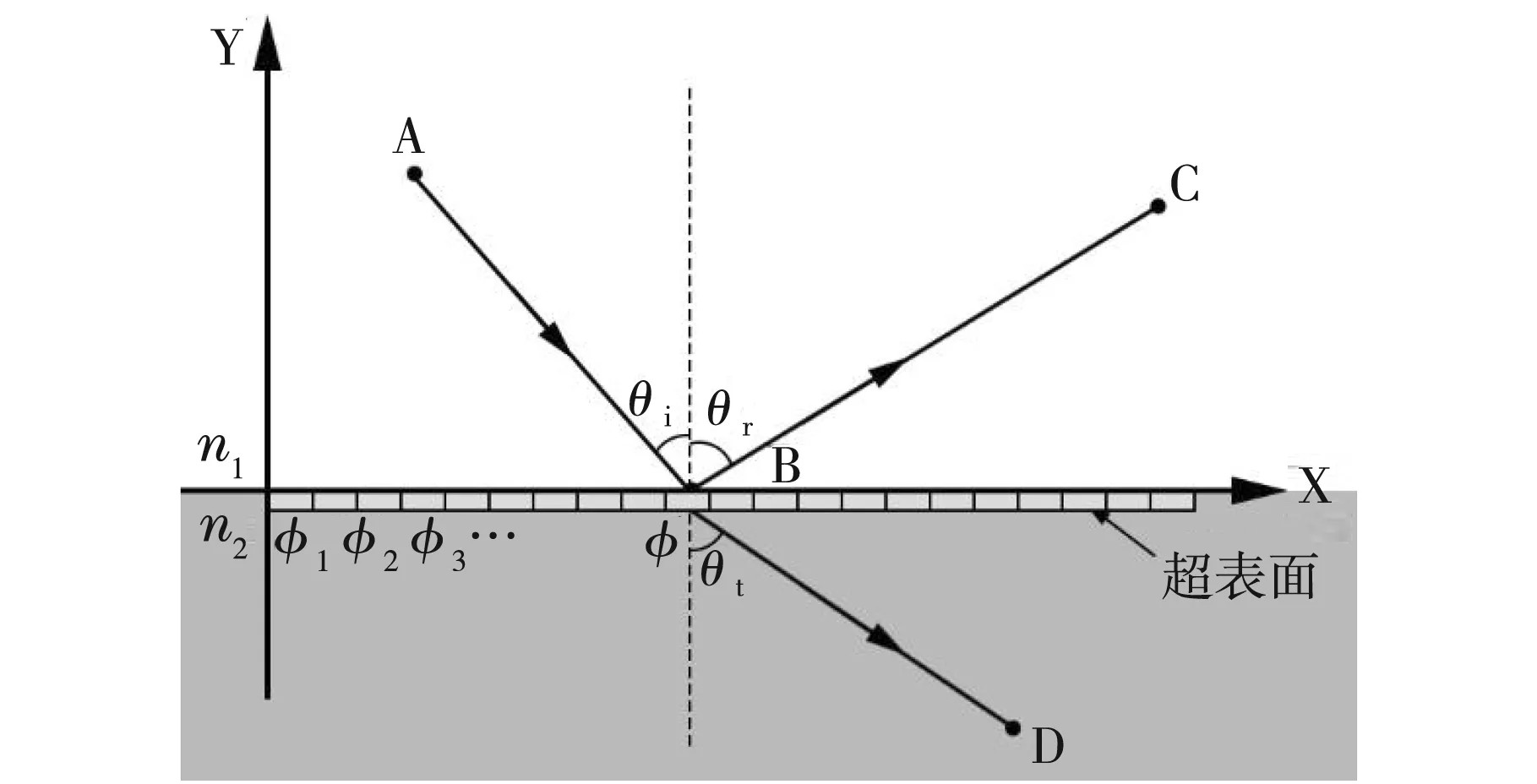
图2 超表面的反射、折射原理示意图

从波动的角度分析，波的传播过程反映的是相位的变化，因此“最短时间原理”也可描述为波传播的真实路径应使其相位变化取极小值。由于此时超表面上的B点本身就引入了一个额外的相位延迟φ，因此根据公式(1)，波从A点出发，经过B点反射到C点的过程中，总的相位变化应为：

Φ1=k0S1+φ

(7)

其中，k0为波数。将Φ1对x求导并取其导数为0得[7]：

(8)

(9)

由公式(9)可以看出，此时的反射角不仅和入射角有关，还和波数、介质折射率和超表面所引入的相位延迟在X轴上的梯度分布情况有关。这里我们通常设定波数和介质折射率为常数，那么当超表面上的相位延迟沿X轴等间距递增或递减时(即dφ/dx为一定值)，超表面上每一点处的反射角均能保持一致且为一定值；而当dφ/dx为一变值时，超表面对入射波的反射将呈现复杂多变的形式，此处关于这部分内容不再详述。需要指出的一点是，我们所熟知的半波损失并不会对超表面的反射结果产生影响，因为各点由于半波损失而产生的相位差值都是相同的，并不会在X轴上产生梯度变化。

下面我们通过举例简单介绍dφ/dx为一定值时的反射情况。不妨设波的传播介质为空气，即折射率n1=1。超表面的相位延迟在X轴上等间距递增的同时，将以2π为单位进行周期性变化，这里设定相位延迟改变一个周期对应在X轴上前进的长度为Γ=2λ0，λ0为入射波长，则dφ/dx=π/λ0，根据公式(9)，反射角可表示为：

θr=arcsin(sinθi+0.5)

(10)

根据公式(10)，我们可以绘制出超表面在上述相位延迟条件下的反射角与入射角的关系图。

图3分别给出了常规表面和超表面对不同入射角的反射情况。其中，右下角的插图为入射角和反射角的符号标注原则示意图，当入射波在法线的左侧时为正，右侧为负；当反射波在法线右侧时为正，左侧为负。从图中可以直观地看出，超表面的反射角不再和入射角相等。例如，当波垂直于超表面入射时，产生的反射角为30度；当波为-30度入射时，反射却垂直于超表面出射；当入射角大于30度时，反射波只能沿着超表面传播，而不能向远场辐射。尤其值得注意的是曲线在第二象限中的灰色部分，在此区域内，反射波和入射波处在法线的同侧，即出现了负反射现象。这些规律和我们熟知的常规表面反射规律截然不同，因此老师们在讲课中通过这部分内容的渗透，能够极大地激发学生对这些新奇现象的探索热情和对新理论的学习兴趣，并且能够使学生对所学知识产生更深刻的认识和见解。

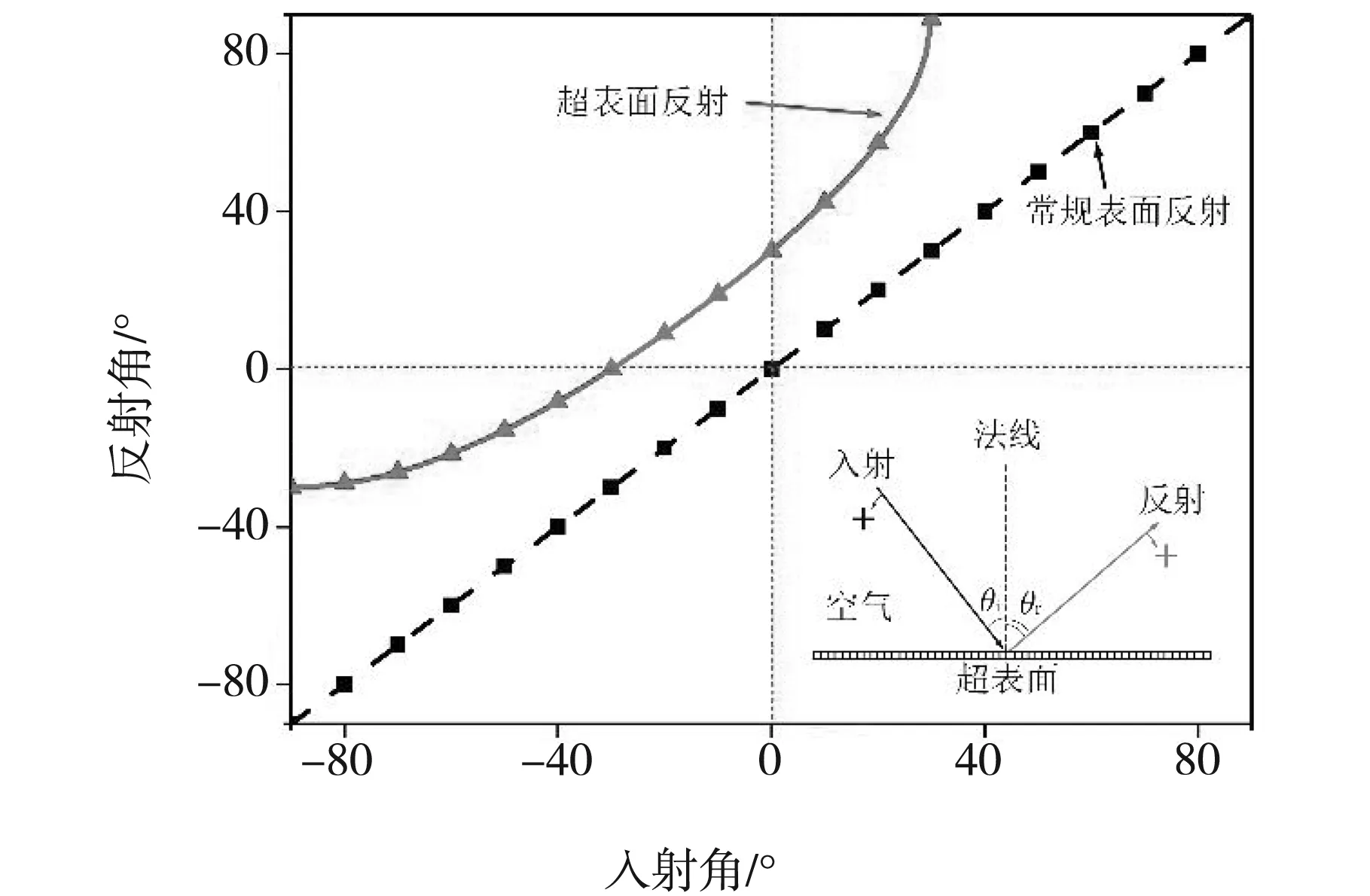
图3 超表面和常规表面的反射角与入射角的关系图

超表面对入射波的折射规律推导原理与上述过程类似，在此不再赘述。推导出的折射角公式如下[7]：

(11)

3 超表面的构建方法

3.1 超表面中人工基元的设计原理

我们可以利用等效电路的知识对超表面人工基元的设计原理进行定性分析[8]。当波在各向同性的均匀介质中传播时，该介质可以被等效成为一个具有恒定阻值的电阻，同时入射波可以被等效成为一个交变电压，则经过该介质的波与入射波之间不会产生相位延迟。但是，如果我们将均匀介质替换成为具有特定形状和结构的人工基元，由于构成人工基元的材料与其周围的介质之间存在边界效应，那么该基元不能再被简单地等效成一个电阻，而应该被看成是电感和电容的耦合，并最终产生一等效阻抗，此时的等效阻抗将会导致经过该基元的波与入射波之间产生一定的相位延迟。基元的结构、形状和尺寸的差异将会导致相位延迟大小的不同，因此可以通过优化基元的结构参数来实现其相位延迟从0到2π的变化。通常情况下，单个人工基元的结构尺寸是远小于波长的，因此可以把由这种单层基元有序排列而成的介质近似地看作是均匀介质表面，只是其等效阻抗与常规介质存在差异而已。

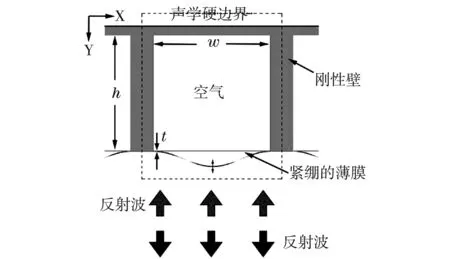
需要指出的是，虽然在大学物理中，反射和折射定律出现在了几何光学部分，但是这些规律对所有类型的波均适用，包括电磁波、声波和机械波等。由于声波是纵波，相对于电磁波而言不涉及极化、偏振等问题，以声波为案例来进行超表面基元的讲解将更能突出问题的重点，并且更容易被学生所理解和掌握，因此我们选取了一种典型的声学超表面模型为例来详细讲解基元的设计思路，如图4所示[9]。其中，图4(a)展示了基元的二维模型示意图，它是由一个下端开口的空腔和一个用来封住开口部分的橡胶薄膜组成的。其中，入射声波波长λ0=92.7 mm。空腔的高度h=10 mm，空腔宽度w在6.5 mm至10 mm之间取值。薄膜厚度t=0.07 mm，薄膜的质量密度、杨氏模量和泊松比分别为920 kg/m3、6.9×109 Pa和0.36。当声波从下向上入射到该基元上时，基元可以被等效为多个电感与电容的耦合[10]，因此基元会由于存在等效阻抗而对入射波产生相位延迟。通过改变基元内空腔的宽度w，即可改变其阻抗，进而在0至2π之间实现不同的相位延迟，如图4(b)所示。

(a)

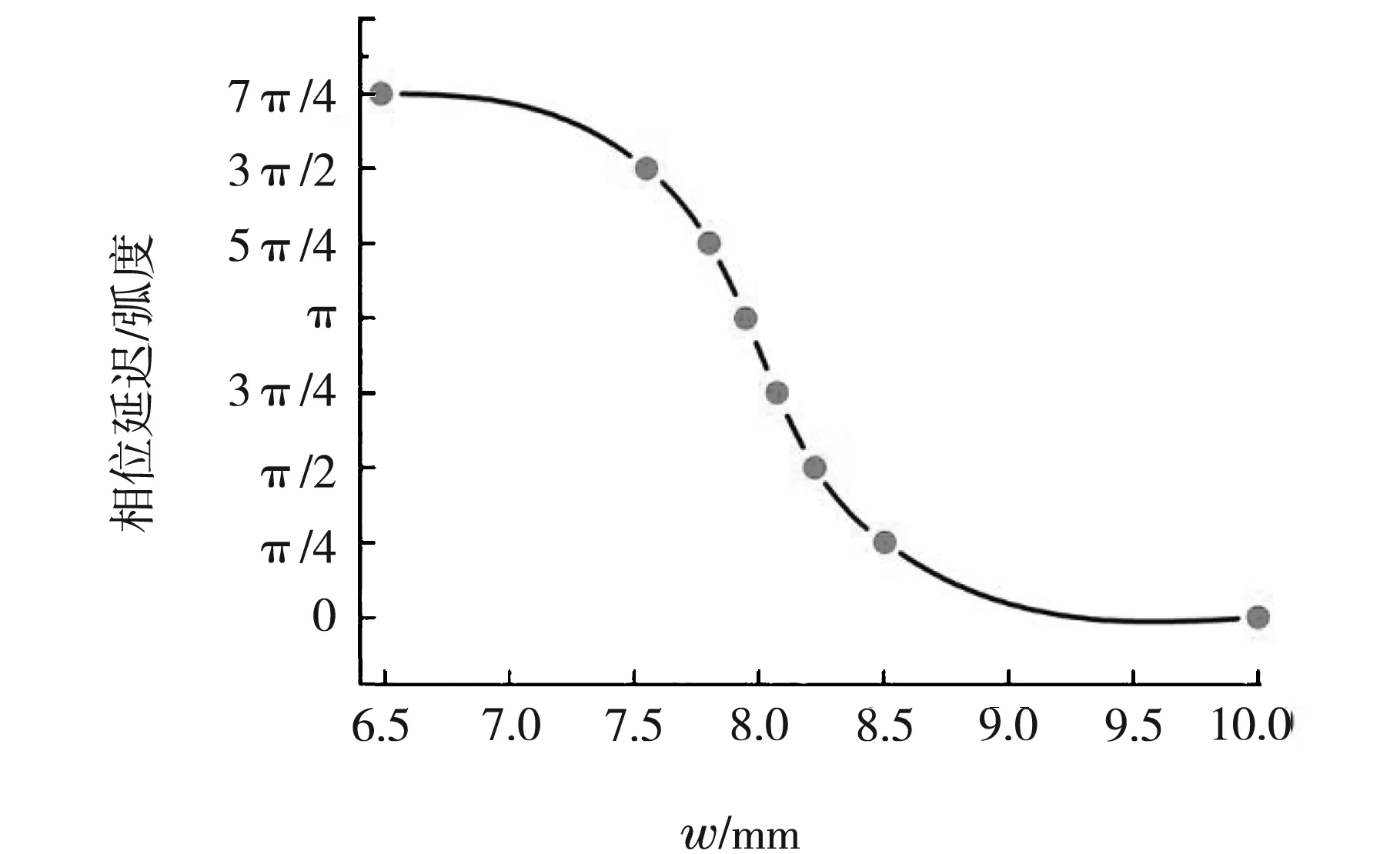
(b)图4 声学超表面基元模型结构示意图及其反射相位延迟与w的变化关系[9]

3.2 基元的有序排列

在图4(b)中，虽然我们可以得到相位延迟与w之间的连续变化关系，但是考虑到每个基元的宽度并不是无限小量，因此实际构建超表面的时候只能选取有限个离散的基元来实现相位延迟在0到2π之间等间距的变化。通常情况下选取8个基元分别实现0、π/4、π/2、3π/4、π、5π/4、3π/2和7π/4的相位延迟，在此模型中对应的w取值分别为10 mm、8.504 mm、8.224 mm、8.072 mm、7.947 mm、7.801 mm、7.549 mm和6.485 mm，在图4(b)中的曲线上以圆点表示[9]。下面我们就结合该基元模型，以周期长度Γ=2λ0=185.4 mm为例来说明如何将不同基元进行有序排列来实现超表面上的梯度相位延迟，如图5所示。由于在8个选定的基元中，最大的基元宽度也没有超过10 mm，而每隔Γ/8(此处为23.175 mm)的距离上就应产生π/4的相位延迟，因此为了充分利用空间，我们在每个Γ/8区间内放置两个相同的基元。随着位置不断向右推进，依次摆放两个所需基元即可，直至将本周期排满，下一周期按此规律循环往复。通过基元的这种有序排列，我们就成功构建出了具有图3所示性质的超表面。

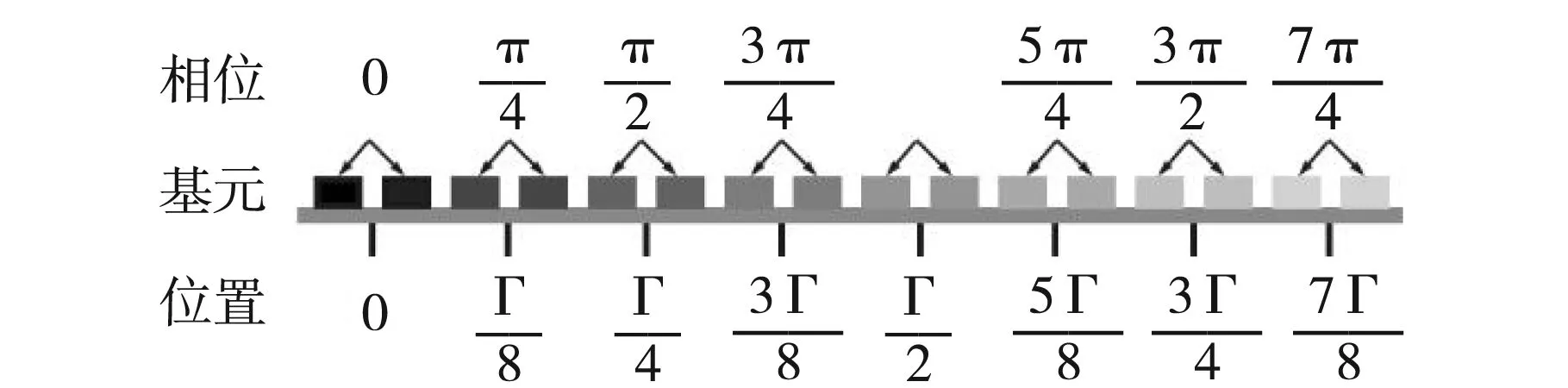
图5 声学超表面基元有序排列方法示意图

由此可见，超表面的设计原理并不复杂，因此老师可以引导学生在课下进行深入探索，利用科学的手段自行设计基元模型，构建超表面，研究其反常反射或反常折射性能，这一过程既有助于激发学生们的创新能力，也有利于提高他们的科学素养。

4 结 语

在新工科建设的背景下，基础教学与前沿科学的有机融合已迫在眉睫。本文希望通过对超表面反常反射和折射规律的简要介绍，将物理学前沿的科研成果融入大学物理的授课内容中，使学生在掌握基础物理学知识的基础上，开拓自己的科学视野，打破对物理知识的常规理解，培养科学严谨的思维方式，增强原始创新能力，为将来在各学科中从事科学研究打下重要的基础。也希望通过本文对超表面理论的浅显讲解，能够有助于丰富课堂内容，激发学生的学习兴趣，同时为大学物理的授课老师提供新颖的教学素材。