SRC柱纤维单元塑性铰长度的计算分析

刘中欢，吴梓楠

（华南理工大学土木与交通学院，广州 510640）

基于性能的抗震设计依赖于准确的结构非线性分析模型［1］，纤维单元因其高效的计算效率被广泛运用到结构非线性分析模型中.根据计算方法的不同，纤维单元可分为基于刚度法的纤维单元和基于柔度法的纤维单元两大类.基于刚度法的纤维单元利用线性Lagrange插值构造轴向位移场，利用Hermite插值构造切向位移场，单元内部存在常值轴向应变和线性曲率问题.基于柔度法的纤维单元则利用线性插值来求取截面弯矩，再通过截面柔度矩阵来求取截面变形，因此可有效避免线性曲率问题.但当模拟强度软化的构件时，柔度法纤维单元由于塑性无法扩散而存在明显的塑性局部化问题，导致数值模拟难以收敛.

为解决柔度法纤维单元塑性局部化的问题，Coleman等［2］提出修正混凝土断裂能的方法，其修正公式中包含端部积分点的权重项，对于积分点权重值不同的构件，需要分别对其混凝土本构进行修正，因此该方法在使用上较为困难.Scott等［3］则通过使用Gauss-Radau积分来解决柔度法纤维单元塑性局部化问题，该方法在实际工程中更具可操作性.Gauss-Radau积分固定了端部积分点的权重，即事先指定了塑性铰长度，因此塑性铰长度的选取将直接影响到柔度法纤维单元的求解结果.

国内外学者对钢筋混凝土构件的塑性铰长度计算方法均有研究.如Priestley和Park［4］在1987年提出了考虑框架柱高和纵筋直径的塑性铰长度计算方法，随后Paulay和Priestley［5］通过考虑不同强度等级的纵筋影响，对Priestley和Park提出的塑性铰长度计算表达式进行了修正.沈聚敏等［6］通过钢筋混凝土梁的试验得出弯曲和压弯构件的塑性铰长度在0.2～0.5倍梁高之间.袁必果［7］提出了考虑偏心距影响的压弯构件塑性铰长度计算公式.此外，还有部分学者分别在塑性铰长度计算公式中考虑了配筋率、钢筋类型和剪应力密度等因素的影响［8-10］.但现有公式大多是针对钢筋混凝土构件提出的，在型钢混凝土柱中的适用性依然有待研究.王斌等［11］根据试验结果通过推导塑性转角的方法获得了适用于型钢混凝土柱的等效塑性铰长度计算公式，该公式与试验结果匹配较好，但由于计算参数较多，所以将其直接运用于柔度法纤维单元的计算中尚有一定难度.

型钢混凝土柱作为典型的强度软化构件，塑性铰长度的合理选取将直接影响柔度法纤维单元的数值模拟精度.本文基于44个型钢混凝土柱的试验数据，回归适用于型钢混凝土柱柔度法纤维单元的塑性铰长度计算公式，并基于该回归公式探究了轴压系数（试验轴压比）、体积配箍率和含钢率对型钢混凝土柱延性的影响.

1 柔度法纤维单元

1.1 基本理论

基于柔度法的纤维单元是假定在节点力的作用下，单元内部的轴力和剪力均为常值，并利用线性插值来求取各积分点处的截面弯矩.柔度法纤维单元的插值函数如式（1）所示，通过该插值函数可使单元力转化为截面力，再利用上一迭代步的截面柔度矩阵f(x)来求解截面变形e(x)，如式（2）所示.然后通过数值积分（如式（3）和式（4）所示）分别求解单元柔度矩阵和单元变形.最后，根据单元柔度矩阵和单元变形求解单元抗力，抗力与外力之间的不平衡力将重新插值到截面中进行迭代，直至满足容差要求.

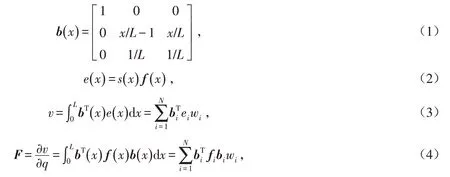
式中：b(x)为柔度法纤维单元的插值函数；L为单元长度；x为单元中插值函数的计算位置；e(x)为截面变形，s(x)为截面内力；f(x)为截面柔度矩阵；v为单元端部位移；wi为积分点权重系数；F为单元柔度矩阵；q为广义节点力.

1.2 塑性局部化问题

对于强度软化的构件，由于受到插值函数的影响，当柔度法纤维单元端部积分点发生强度软化时，其余积分点处的截面弯矩值也将随之减小，即发生了卸载现象.随着构件强度的逐步软化，仅有端部积分点的曲率增加，而其余积分点的曲率将逐渐减小，如图1所示.此时，构件的塑性将集中在端部积分点，端部积分点的权重等同于塑性铰长度的概念.因此，对于强度软化问题，端部积分点的权重将直接影响着构件强度的软化速率，需选择一个合理的端部积分点权重（即塑性铰长度lp），以提高柔度法纤维单元的模拟精度.

图1 柔度法纤维单元的塑性局部化问题Fig.1 Plastic localization of fiber element based on flexibility method

2 基于试验的塑性铰长度分析

2.1 分析方法

为更好把控端部积分点的权重值，将通过Gauss-Radau积分方法来进行型钢混凝土柱的推覆分析.Gauss-Radau积分方法固定了端部积分点的权重值，使该权重值不随着型钢混凝土柱长度的增加或积分点数目的增加而变化.由于端部积分点的权重（即塑性铰长度）直接影响构件强度的软化速率，因此以软化刚度Ksoft为指标，通过试验数据来确定数值分析模型的塑性铰长度值.软化刚度Ksoft计算公式如式（5）所示.

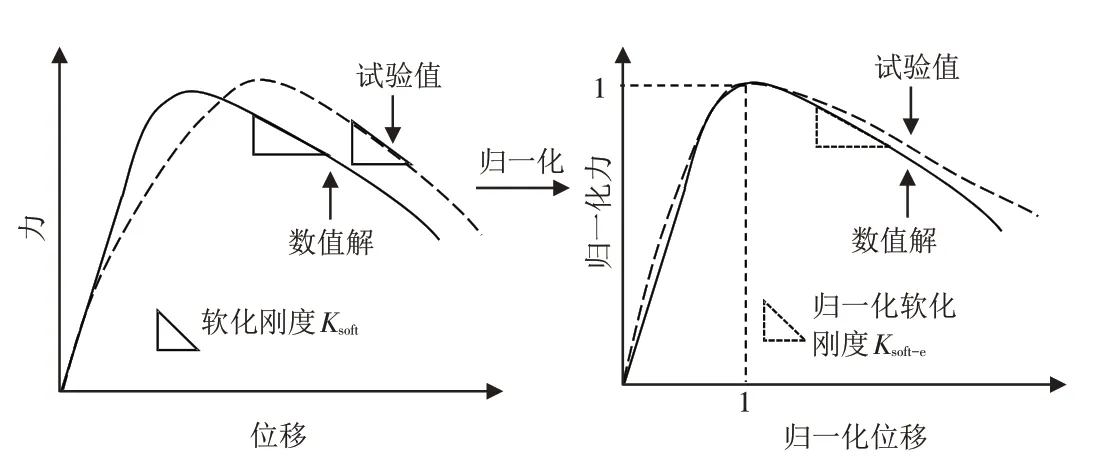
图2 骨架曲线软化刚度示意图Fig.2 Sketch of the softening stiffness of the skeleton curve

式中：Fmax为峰值承载力；Fu为极限承载力，取值为0.8倍的Fmax；Dmax为峰值承载力对应的位移值；Du为极限承载力对应的位移值；R为软化刚度与峰值承载力割线刚度的比值.

试验值与数值解在峰值承载力和峰值位移上会有所偏差，这种偏差会直接影响软化刚度Ksoft的值.为使软化刚度更具客观性，将骨架曲线的峰值承载力和峰值位移进行归一化，如图2所示.此时归一化软化刚度的计算公式Ksoft-e如式（6）所示.

为更直观地反映归一化软化刚度Ksoft-e，本文提出软化角θsoft概念.软化角θsoft为归一化软化刚度Ksoft-e的反正切值，其量纲为rad，计算公式如式（7）所示.本文将以软化角θsoft为指标来衡量柔度法纤维单元模拟的准确性，进而确定与试验软化角θ最为相符的塑性铰长度值.

2.2 基于试验的数值分析

本文共收集44个型钢混凝土柱的试验数据，试验构件参数如表1所示.根据试验骨架曲线，经归一化后可得到试验软化角θ，其变化范围一并列入表1.

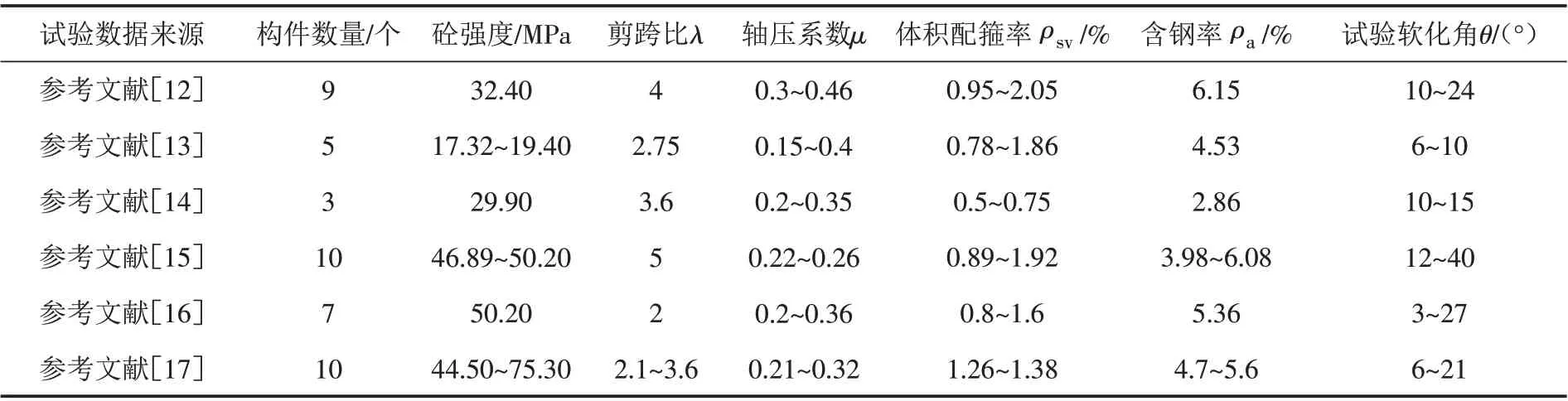
表1 44个型钢混凝土柱的试验参数及试验软化角Tab.1 Test parameters and test softening angles of 44 steel reinforced concrete columns

以型钢混凝土柱SRC1-2为例，通过单元塑性铰长度的增量改变，基于OpenSees平台进行推覆分析以确定各个塑性铰长度下构件的力-位移曲线，进而可确定软化角θsoft，从中挑选出与试验软化角θ最为接近的θsoft，其对应的塑性铰长度值即为该构件柔度法纤维单元数值模拟的合理塑性铰长度.不同塑性铰长度下SRC1-2构件的力-位移曲线如图3所示，当柔度法纤维单元的塑性铰长度为60 mm时，其软化角θsoft与试验软化角θ最接近，即60 mm为该构件数值模拟的合理塑性铰长度.

44个型钢混凝土柱的合理塑性铰长度计算结果如图4所示，曲线与试验点重合的位置为θsoft等于θ的位置，此时曲线对应的横坐标即为该构件数值模拟的合理塑性铰长度，44个型钢混凝土柱数值模拟的合理塑性铰长度变化范围为25～75 mm.

图3 SRC1-2构件在不同塑性铰长度下的力-位移曲线Fig.3 Force-displacement curves of SRC1-2 member under different plastic hinge lengths

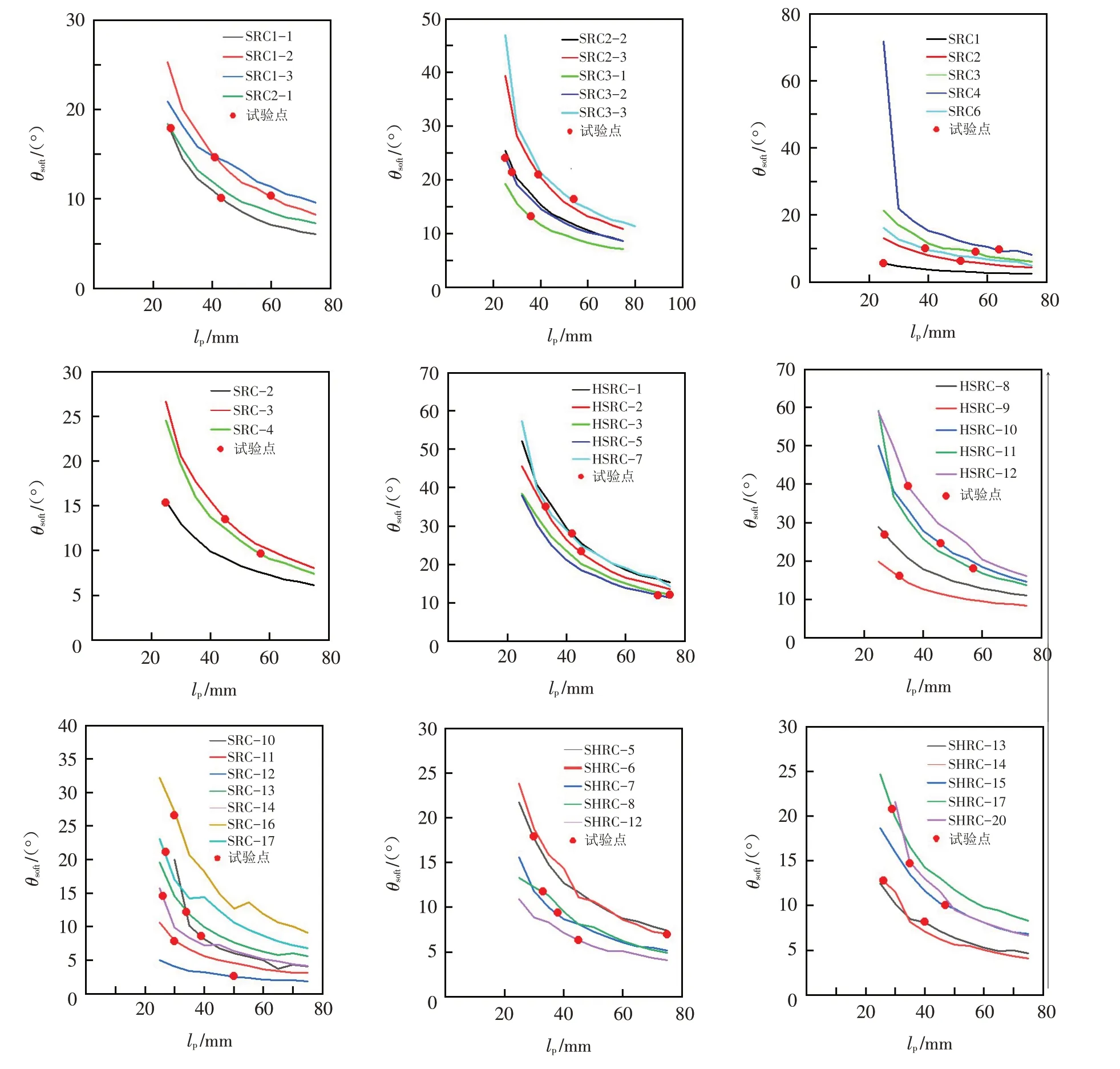
图4 44个型钢混凝土柱数值模拟的合理塑性铰长度Fig.4 Reasonable plastic hinge length of 44 steel reinforced concrete columns in numerical simulation

3 塑性铰长度计算公式的回归

3.1 确定回归公式的基本参数

国内外常用的钢筋混凝土构件的塑性铰长度经验公式如表2所示.提取表2中量纲与塑性铰长度量纲相同的参数于表3中，并将与钢筋混凝土构件相关的变量转化为型钢混凝土构件相关的变量，作为回归塑性铰长度计算公式的基本参数.其中，将剪应力密度r（MPa）转换为无量纲参数剪压比v，剪压比计算公式如式（8）所示.

式中：fck为混凝土轴心抗压强度标准值，MPa.

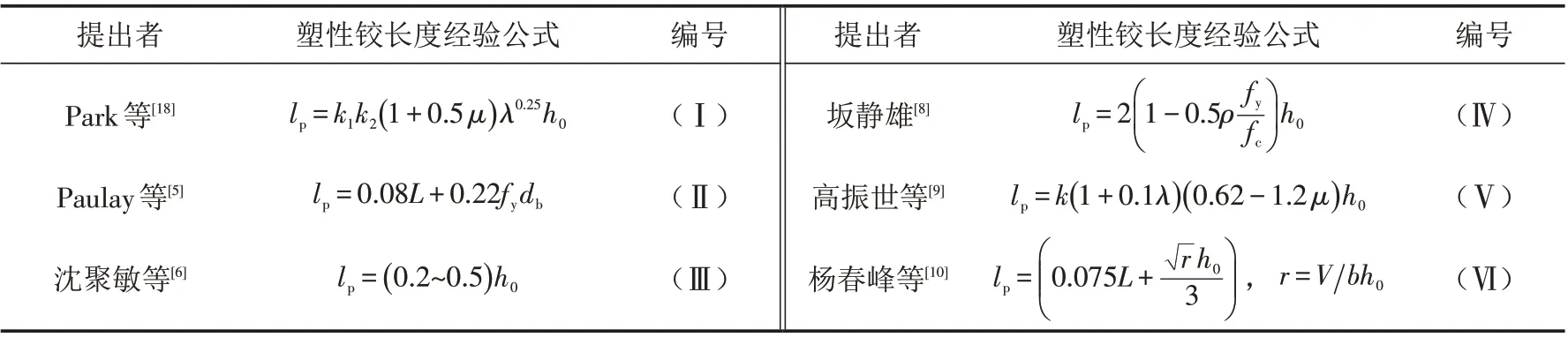
表2 常用钢筋混凝土构件的塑性铰长度公式Tab.2 Commonly used plastic hinge length formulas of reinforced concrete members

根据前人的试验结果可知，构件的延性随着轴压系数的上升而减弱.为保证柔度法纤维单元在数值模拟时能满足上述规律，对含轴压系数的参数进行适当调整，调整结果列于表3中.其中，参数6的取值区间较小，不具备统计意义，因此在回归分析中，不考虑参数6对塑性铰长度计算公式的影响.

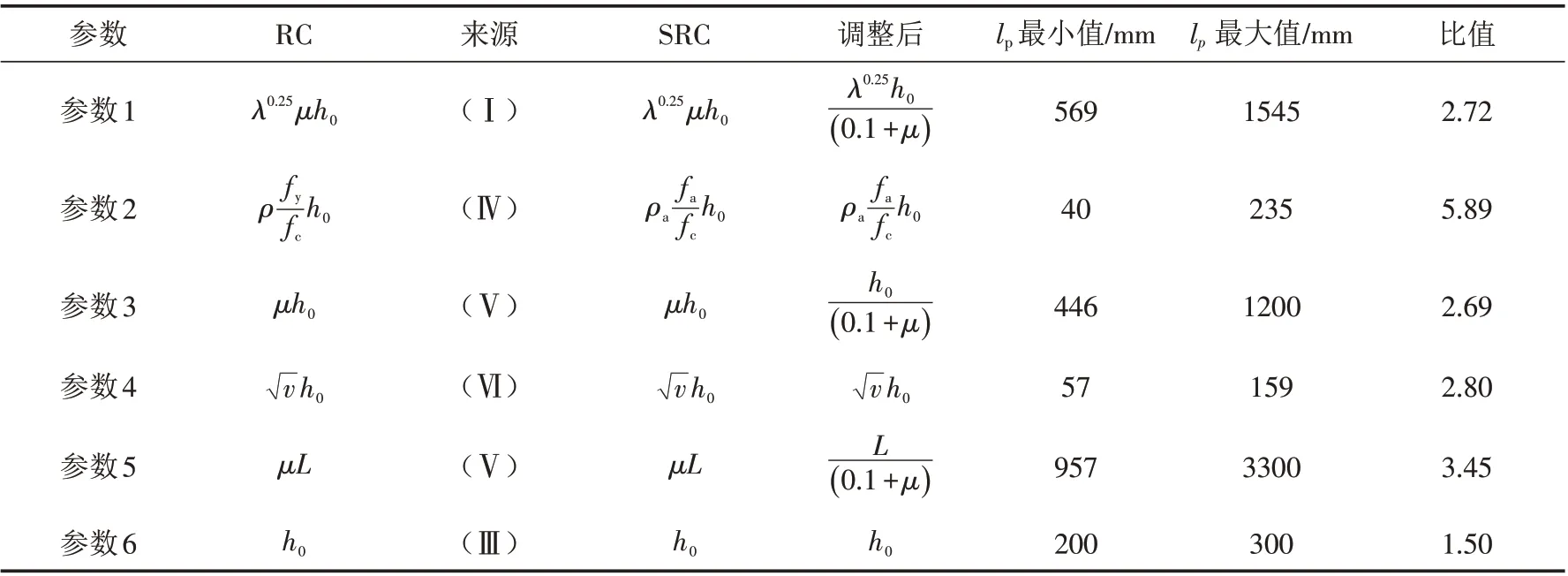
表3 SRC柱塑性铰长度计算公式的基本参数及其取值区间Tab.3 Basic parameters and value intervals of calculation formulas for plastic hinge lengths of SRC columns

3.2 塑性铰长度计算公式的回归

利用前文3.1小节提出的5个基本参数，回归基于柔度法纤维单元的双参数型钢混凝土柱塑性铰长度计算公式.将5个基本参数两两进行组合，回归确定各参数的系数项和各组合的相关系数R，回归结果如表4所示.由表4可知，组合10的相关系数R值最大，回归效果最优，因此提出基于柔度法纤维单元的塑性铰长度lp计算公式如式（9）所示.

式中：v为剪压比；λ为剪跨比；μ为轴压系数；h0为截面有效高度，mm.

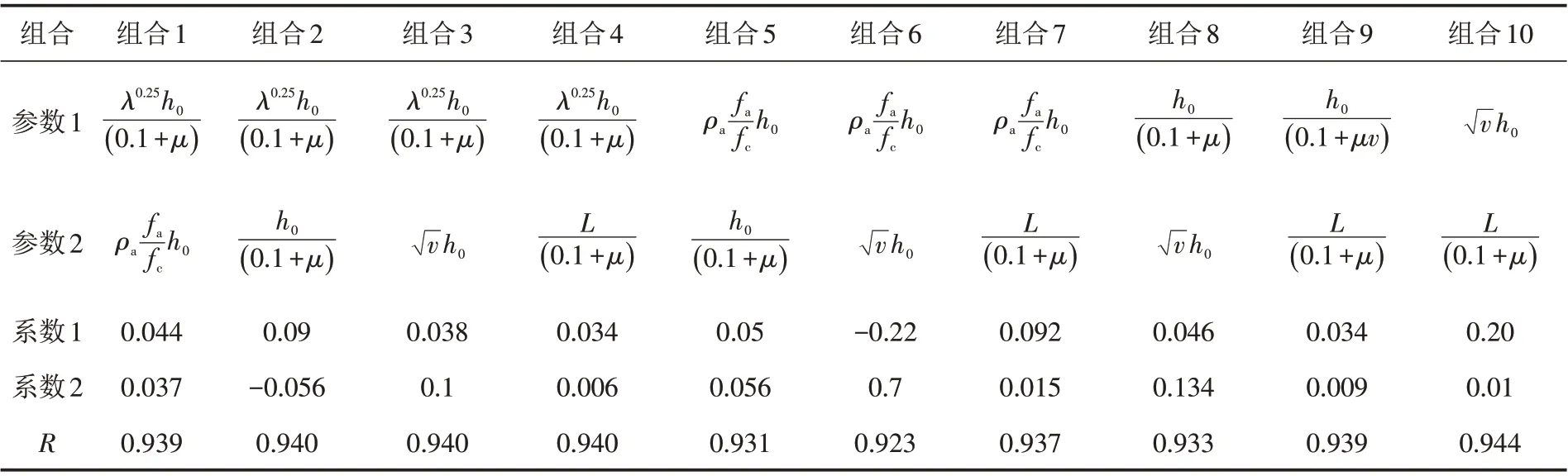
表4 SRC柱塑性铰长度计算公式回归分析Tab.4 Regression analysis of calculation formulas for plastic hinge lengths of SRC columns

4 延性分析

4.1 延性系数的确定

延性是表征构件变形能力的重要参数，延性系数μDuc则是量化构件延性的重要指标，其计算公式如式（10）所示.

式中：Δy为屈服位移，mm；Δu为极限位移，mm.在本文中Δu的取值为0.8倍峰值承载力对应的位移值.

型钢混凝土柱并非理想弹塑性体，其骨架曲线上没有明显的屈服点，因此常取等效屈服位移作为构件的屈服位移.常用的确定等效屈服位移的方法有3种，分别为通用屈服弯矩法（作图法）、Park法和能量等效法.其中能量等效法物理含义明确，因此本文采用能量等效法来计算构件的等效屈服位移.

4.2 构件设计

为探究轴压系数μ、体积配箍率ρsv和含钢率ρa对构件延性的影响，采用C40混凝土和Q235级型钢设计了24个型钢混凝土柱，构件长度均为1200 mm，截面尺寸均为400 mm×400 mm，剪跨比均为3.设置轴压系数分别为0.2、0.3、0.4、0.5、0.6、0.7，体积配箍率分别为0.5%、0.78%、1%，含钢率分别为5.6%、7.3%、10.7%，然后依据公式（10）分别计算24个构件的延性系数.

4.3 轴压系数对型钢混凝土柱延性的影响

延性系数随轴压系数的变化情况如图5所示.由图5可知，轴压系数是影响型钢混凝土柱延性的重要因素，延性系数随着轴压系数的升高而降低；当轴压系数大于0.4时，μDuc-μ曲线出现明显拐点，此时延性系数较小，轴压系数对型钢混凝土柱延性系数的影响逐渐减弱.

4.4 体积配箍率对型钢混凝土柱延性的影响

延性系数随体积配箍率的变化情况如图6所示.由图6可知，延性系数随着体积配箍率的增加而增大，且随着轴压系数的增加，体积配箍率对型钢混凝土柱延性系数的影响逐渐减弱.

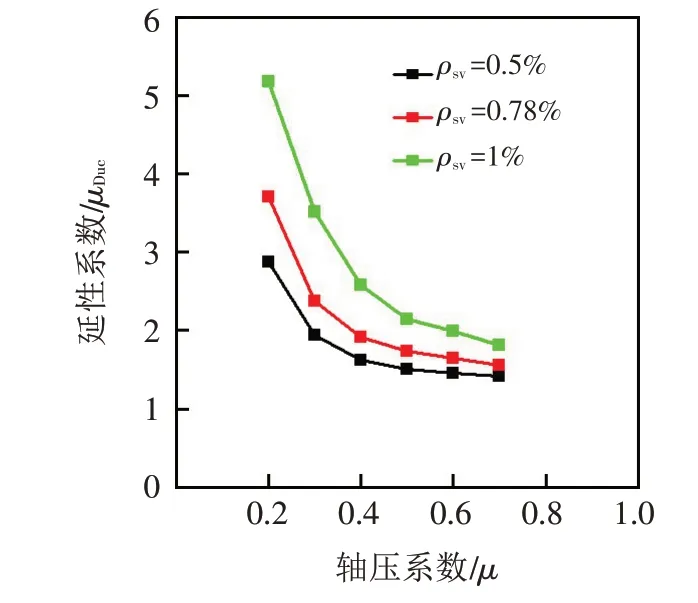
图5 μDuc-μ曲线Fig.5 μDuc-μcurves

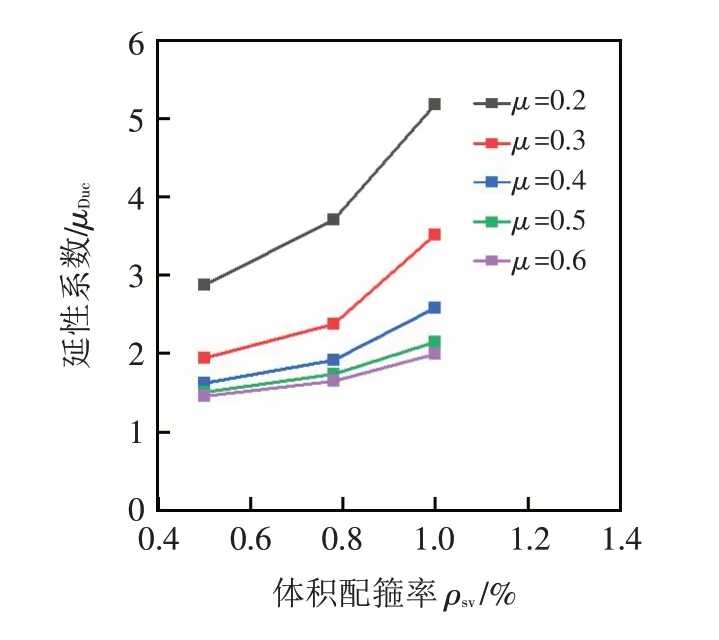
图6 μDuc-ρsv曲线Fig.6 μDuc-ρsv curves

4.5 含钢率对型钢混凝土柱延性的影响

延性系数随含钢率的变化情况如图7所示.由图7可知，延性系数随着含钢率的增加而增大，但增大效果并不明显，即含钢率对型钢混凝土柱延性系数的影响并不显著.

图7 μDuc-ρa曲线Fig.7 μDuc-ρa curves

5 结论

本文基于44个型钢混凝土柱的试验数据，回归了基于柔度法纤维单元的塑性铰长度计算公式，可有效地解决柔度法纤维单元的塑性局部化问题，同时基于回归公式探究了轴压系数、体积配箍率和含钢率对型钢混凝土柱延性的影响.得出以下结论：

1）在模拟构件的强度软化行为时，柔度法纤维单元存在塑性局部化问题，塑性无法扩散，因此端部积分点权重（即塑性铰长度）会直接影响数值模拟结果.

2）基于44个型钢混凝土柱的试验数据，提出了适用于柔度法纤维单元的塑性铰长度计算公式，有效地解决了柔度法纤维单元的塑性局部化问题.

3）轴压系数是影响型钢混凝土柱延性的重要因素，其延性系数随着轴压系数的升高而降低，当轴压系数大于0.4时，轴压系数对构件延性的影响逐渐减弱；型钢混凝土柱延性系数随着体积配箍率的增加而增大，且随着轴压系数的增加，体积配箍率对构件延性的影响逐渐减弱；含钢率对型钢混凝土柱延性基本没有影响.