随机规划问题最优值的收敛性分析

刘晋纹，韩有攀

（西安工程大学理学院，西安 710600）

现实生活中，一些事件虽然发生的概率很小，但是一旦发生就会产生很大的影响，例如金融危机、自然灾害等.而大偏差理论为计算稀有事件的概率提供了一个很好的方法.因此作为概率论极限理论重要分支的大偏差理论，受到了越来越多学者的广泛重视.大偏差理论最早起源于19世纪70年代的Boltzmann理论，随后得到不断发展，其中最有影响力的人物是2007年度“阿贝尔奖”获得者、美籍印度数学家、纽约大学教授Varadhan，他为概率论研究方面作出了突出贡献，特别是他的大偏差理论成为现代概率论的基石.他与Stroock关于扩散过程的研究成果以及与Donsker在大偏差方面的合作研究成果尤为出色.目前的大偏差理论体系较为丰富，重要性结论有：有限维、独立同分布随机变量的大偏差原理，即Cramér定理［1］；有限维、非独立同分布随机变量的大偏差原理，即Gärtner-Ellis定理［2］；测度空间的大偏差原理，即Sanov定理［3］；函数空间的大偏差原理，即Schilder定理［4］等.

随机规划所研究的对象是含有随机因素的数学规划问题，是运筹学的一个重要分支.最早提出随机规划问题的是线性规划创始人之一Dantzig，他在航班最优次数的问题中发现客流量是个随机变量，最先提出了二阶段有补偿随机规划问题.目前关于随机规划的成果很多，可参看著作［5-9］和综述论文［10-14］等.用样本均值逼近（SAA）方法去解决随机规划问题是一种十分有效的方法，其基本思想是用样本均值来估计目标函数的期望函数.2016年，Yang等［15］采用CVaR逼近将模型等价转化为凸优化模型，然后运用样本平均逼近方法进行求解，证明了算法的收敛性，数值结果表明了模型和算法的有效性；2017年，Pour等［16］应用样本平均近似技术来解决标准人员分配问题的一个实际推广问题；2019年，Yang等［17］提出了一种基于SAA的不可行内点算法的随机互补问题，研究了算法的收敛性和计算复杂度；2008年，Homem-de-Mello［18］曾结合LHS抽样和拟蒙特卡罗方法研究了非独立同分布样本下原问题与样本平均逼近问题最优值、最优解的收敛性.

利用大偏差原理来研究随机规划问题的收敛性也取得了一系列成果.假设样本为独立同分布（independently identically distribution，i.i.d）时对随机规划模型的研究：1995年，Kaniovski等［19］利用大偏差理论导出了随机优化问题近似解收敛的几个指数界，基本结果表明，用经验分布代替原分布得到的解为求解随机规划问题提供了有效的工具；2000年，Dai等［20］考虑了两阶段随机规划问题，用其经验平均值代替要优化的性能函数，利用大偏差技术建立了经验最优与性能函数最优的偏差概率的指数收敛性；2008年，Shapiro［21］研究了i.i.d样本下极大极小随机优化问题与其样本均值逼近问题最优值的渐进性并举例讨论了风险规避随机规划SAA的渐进性半偏差风险度量，随后利用大偏差原理证明最优值一致指数收敛性；Shapiro和Xu［22］研究了带有均衡约束的随机规划问题的最优解集和最优值的收敛性，且证明了原问题与其SAA问题的一致指数收敛性；2011年，Ralph和Xu［23］探讨了针对一系列仅仅是上半连续和从上部逐点Calm的随机函数的一致指数速率收敛，并且应用于两阶段随机优化问题的稳定性分析中.假设样本为非i.i.d时对随机规划模型的研究：2010年，Xu［24］将i.i.d样本推广到一般情况下，证明了通常的随机规划问题与其SAA问题的一致指数速率收敛；2013年，孙海琳［25］在Xu的基础上将一致全局Hölder连续条件弱化为局部Hölder连续，研究了一般样本下随机规划问题与其SAA问题的一致指数速率收敛.

在此基础上，当样本为非独立同分布时，我们研究通常的随机优化问题和极小极大随机优化问题最优值的指数收敛性.

1 预备知识

考虑如下随机优化问题：

其中X是Rn中的非空闭集，ξ是一个概率分布支撑集为D∈Rd的随机向量，F(x,ξ):X×D→R是Caratheodóry函数，即集合X上连续且在D上可测.期望函数f(x)是确定的并且在所有x∈X的值是有限的.

取一组随机向量ξ的样本ξ1,ξ2,…,ξN对此函数进行估计.得到SAA问题：

由文献［26］中的定理2可知以下引理.

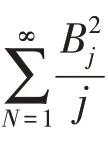
证明见文献［27］中的第5章.

定义1 给定两个集合A，B，则A与B之间的偏差表示为

若A是空的，则dist(x,A)=+∞，因此若B是空的，则dist(A,B)=+∞.

2 随机规划问题

引理3 若存在紧集C⊂RN使得：

1）问题（1.1）的最优解集S*非空且S*⊂C.

2）f(x)是有限值函数且在C上连续.

为研究随机规划问题的指数收敛性，我们做以下假设：

（A-1）存在一个可测函数L:D→R+使得E[L(ξ)2]有限且

对任意的x，x′∈X，a.e.ξ∈D成立.

注：这个条件是研究随机规划收敛性的一个基本假设，如文献［21，24，28］.当F(x,ξ)为线性随机规划或二次随机规划问题的目标函数时，这个条件成立.

其极限

在0点的一个邻域内所有的t是有限的.

（A-3）随机变量L(ξ)的矩母函数

在0点的一个邻域内的所有的t是有限的.

注：（A-1）在给定的ξ下，目标函数在X上是一致Lipschitz连续的.（A-2）和（A-3）是在研究随机规划问题收敛性标准假设，如文献［18-21］.

定理1 假设条件（A-1）～（A-3）成立并且样本非i.i.d，则对任意ε＞0，存在正实数β=β(ε)与N无关，使得满足下列不等式：

证明 由Gärtner-Ellis大偏差定理可知，对任意的ε＞0

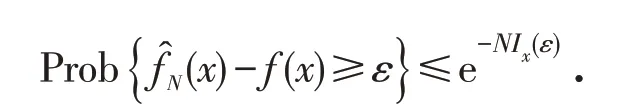
类似可得

因此

且由（A-2）可知Ix(ε)，Ix(-ε)对任意的ε都是正的.

由（3）式两边同时取期望可得

类似可得

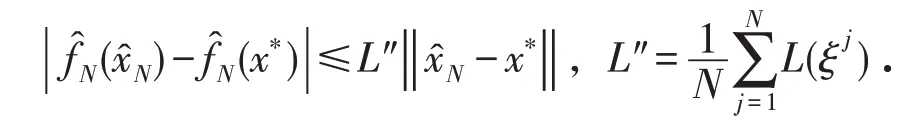
由（A-1）可知L′=E[ ]

L(ξ)是有限的，所以由Gärtner-Ellis大偏差可知，对任意的L‴＞L′，存在正常数λ使得

接着，我们来估计最优值之间的关系，即有

3 极小极大随机优化问题

本节考虑下面极小极大随机优化问题：

其中F(x,y,ξ):X×Y×D→R，ξ=ξ(w)是一个概率分布支撑集为D∈Rd的随机向量.相应的SAA问题为：

（B-1）F(x,y,ξ)是Caratheodóry函数.

（B-2）集合X,Y是非空的并且是紧的.

（B-3）集合X,Y是凸的，函数F(·,·,ξ)在X×Y是凸-凹的，a.e.ξ∈D，即函数F(·,y,ξ)关于X为凸函数，函数F(x,·,ξ)关于Y上为凹函数.

（B-4）期望值函数E[F(x,y,ξ)2]对于任意的(x,y)∈X×Y是有限的，并且存在一个可测函数L:D→R+使得对于所有(x,y)，(x′,y′)∈X×Y，E[L(ξ)2]有限且满足不等式

a.e.ξ∈D成立.

证明 见文献［28，定理2.10］.

定理2 已知条件（B-2）～（B-4）成立，则 |φ(x)-φ(x′)|≤L′‖x-x′‖，其中L′=E[L(ξ)].

证明 由（8）式两边取期望可得

|f(x,y)-f(x′,y′)|≤L′(‖x-x′‖+‖y-y′‖)，L′=E[L(ξ)].

设y是φ(x)的最优解，y′是φ(x′)的最优解，即

φ(x)=f(x,y)，φ(x′)=f(x′,y′)，

则

|φ(x)-φ(x′)|= |f(x,y)-f(x′,y′)|≤ |f(x,y)-f(x′,y)|≤L′‖x-x′‖.

为了建立极小极大随机优化问题最优值之间的一致指数收敛性，还需以下条件：

其极限

在0的一个邻域内的所有的t是有限的.

（B-6）随机变量L(ξ)的矩母函数

在0点的一个邻域内的所有的t是有限的.

注：条件（B-5）和（B-6）是在研究随机规划问题的指数收敛性时所做出的的假设，如文献［20，21-23］等.当随机变量为正态或亚高斯（sub-Gaussian）随机变量，我们可以有如下估计：

由此，我们可以推出（B-5）和（B-6）说成立的.

在上述假设条件下，我们给出以下定理.

定理3 假设条件（B-1）～（B-6）成立并且样本非i.i.d，则对任意ε＞0，存在正实数β=β(ε)与N无关，使得满足下列不等式：

证明 取x*∈Sx，使得

由（B-6）可知L′=E[L(ξ)]是有限的，所以由Gärtner-Ellis大偏差定理可知，对任意的L″＞L′，存在正常数λ使

又因为

由（12）式可得

类似定理1可知

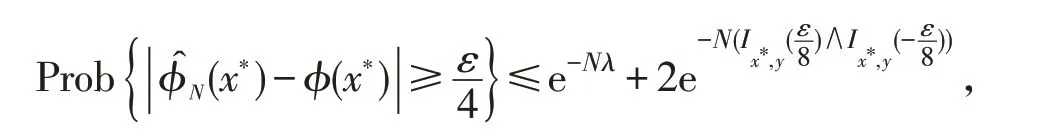
因此

因此

得证.

4 结论

在样本非独立同分布时，对随机规划问题和极小极大随机规划问题最优值的指数收敛进行研究.当随机规划问题目标函数满足全局Lipschitz条件时，利用Gärtner-Ellis大偏差定理建立了两类随机规划问题最优值一致指数收敛的结论.这些结论不仅丰富了随机规划理论的内容，还为求解随机规划问题的算法奠定了理论基础.