基于年月联合分布的典型年径流过程设计计算

刘 进，方国华，方功先，颜 敏

（1.河海大学水利水电学院，南京 210098；2.江苏苏盛工程造价咨询有限公司，南京 210000）

典型年的选取是水能、水利规划设计的基础.在确定典型年的过程中，要合理考虑年径流总量及其年内分配，使之具有丰水年、平水年和枯水年的代表性.通常的做法是，首先对实测径流资料进行频率分析，确定某一设计频率下典型年的总径流量，然后选择几个年径流量与其最接近的实际年份产生典型径流系列，从中选出对水资源供需平衡最不利的径流过程，按同倍比法或者同频率法缩放后作为典型年径流过程.采用上述这种方法设计的径流过程，可能会因人而异，主观经验对结果的影响比较大.为了减少人为因素的影响，相关学者引入系统聚类法，提出采用模糊数学方法选取典型年.夏莉敏等提出一种模糊聚类迭代模型，使水文年选取过程不受主观权重的影响，计算结果相对客观、准确［1］.胡斌奇等基于云模型思想实现了对径流模糊特征的“软划分”，避免了人为确定分类标准的主观性，能够更准确地描述径流的水文丰枯特性［2］.这些研究和理论虽然统筹考虑了年径流总量及其年内分配，但未涉及年、月径流之间的丰枯遭遇概率［3］，使得极端月径流值会对典型年径流过程产生较大的影响，且对于生成的径流过程，也不能确定其是否为设计频率下最有可能的年、月径流组合.

Copula函数是研究变量相依性的工具，可以把年径流分布与各月径流分布有效地结合起来，能够刻画出年、月径流之间的依赖关系，可作为计算年、月径流联合分布，考虑丰枯遭遇概率的一种方法.近年来，Copula函数由于其适用性强、构造灵活、计算简单、对边缘分布形式没有限制等优点，在降雨计算、洪水设计计算、径流丰枯遭遇分析等水科学领域中受到了广泛的应用［4-5］.Zhang等根据美国路易斯安那州阿米特河流域的降雨数据，采用阿基米德Copula函数构建了双变量降雨频率分布模型，并对降雨的联合重现期进行了计算，得出了较为理想的结果［6］.莫淑红等建立了渭河干、支流的径流联合分布，证实了用Copula函数描述干、支流的丰枯遭遇概率问题具有一定的可行性［7］.何庆升等根据长江支流罗田站月径流量资料，研究了高维阿基米德Copula函数在各月径流量联合分布中的应用，并利用Copula函数对径流预测值进行了有效的评价［8］.晋恬等基于阿基米德Copula函数构建了洪峰流量和洪量的二维联合分布，并以此为基础比较了不同重现期标准对于洪水组合设计值的影响［9］.这些研究表明，Copula函数在多变量水文事件中具有很高的应用价值，基于Copula函数构建的联合分布具有较高的可行性.

因此，本文采用阿基米德Copula函数构建年、月径流的二维联合分布（全年与1月径流组合、全年与2月径流组合等），引入条件概率，考虑年、月径流的最有可能组合，研究并验证联合分布在典型年径流过程设计计算中的可行性.

1 径流边缘分布

P-Ⅲ型曲线是我国洪水设计规范中推荐采用的径流分布曲线，少数情况下，频率曲线可以采用其他线型，但要分析论证其可行性［10］.在国外，极值Ⅰ型（Gumbel）曲线和对数正态分布曲线在水文频率计算中也受到广泛应用.选取合适的边缘分布对联合分布的生成至关重要.本文选择P-Ⅲ型曲线、Gumbel型曲线和对数正态分布曲线这3种常用的曲线，对年、月径流的边缘分布进行拟合.采用矩法估计分布参数，根据K-S检验统计量（Dn）、均方根误差（RMSE）和AIC值等统计指标，选取拟合效果最好的边缘分布线型.

2 年、月径流联合分布

径流的年际、年内分布具有不确定性，丰水年可能遭遇枯水月，枯水年可能遭遇丰水月［11-13］.在设计典型年径流过程时，不仅要考虑到年径流总量，还应关注径流的年、月相依性关系，考虑径流的年内分配.Copula函数作为研究变量相关性测度的一种有效的工具，可以将边缘分布和联合分布很好地联系起来［14］.本文基于Copula函数原理，选择年径流和月径流两个变量，构建年、月径流的联合分布.

2.1 常用的Copula函数

总的来说，Copula函数分为t-Copula函数、正态Copula函数和阿基米德Copula函数（Archimedean Copulas）.其中，阿基米德Copula函数由于其形式多样、参数少、易于构造等优点受到广泛的应用，其数学表达式取决于它的构造函数，对于二维的阿基米德Copula函数，其定义如式（1）所示：

式中：C(u,v)为生成的Copula函数；u、v表示变量的边缘分布；φ为构造函数，又称为生成元算子，对于∀t∈[ 0,1)，满足φ′(t)＜0，φ″(t)＞0且有φ(1)=0；φ-1为φ的反函数.可以看出，不同的生成元产生不同的阿基米德Copula函数，生成元的形式决定了Copula函数的最终形式.二维阿基米德Copula函数中常见的主要有Gumbel Copula函数、Clayton Copula函数和Frank Copula函数［15-16］.

1）Gumbel Copula函数

当生成元算子φ=( -lnt)θ，θ∈[1 ,∞)时，对应的Copula函数称为Gumbel Copula函数，其数学表达式为：

2）Clayton Copula函数

当生成元算子φ=t-θ-1，θ∈[ )

0,∞时，对应的Copula函数称为Clayton Copula函数，其数学表达式为：

3）Frank Copula函数

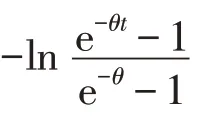
式（2）、（3）、（4）中，θ为Copula函数的参数；t为生成元算子的自变量，通常取联合分布各组成对象的边缘分布；e表示自然对数的底.

2.2 Copula函数的参数估计

Kendall秩相关系数作为描述变量相关性的一个常见指标，可以用来估计Copula函数的参数.当( )

X,Y连续时，Kendall秩相关系数有如下定义：

设(X,Y)的Copula函数为C(u,v)，则有：

联立式（5）、式（6），得：

式（7）建立起了Copula函数与样本的Kendall秩相关系数之间的数量关系，通过这种对应关系来估算Copula函数的参数，是阿基米德Copula函数参数估计的常用方法［17-19］.对于常见的3种二维阿基米德Copula函数，其参数与Kendall秩相关系数的对应关系如表1所示.

表1 常见的二维阿基米德Copula函数的参数估计方法Tab.1 Parameter estimation methods of common two-dimensional Archimedean Copulas

3 条件最有可能径流组合

考虑年、月径流的丰枯遭遇概率，某一特定年径流x下，月径流量yi服从于条件分布FY|X(yi|x).假设条件分布的概率密度函数为fY|X(yi,x)，则fY|X(yi,x)的值越大，表示月径流yi发生的可能性越大，当fY|X(yi,x)的值取到最大值时，认为该径流yi发生的概率最大，对应的(x,yi)为一组最有可能的年、月径流组合［20］.

条件分布概率密度函数如式（8）所示.

4 实例计算

黄河是我国境内的第二长河，发源于青藏高原，全长5464 km，流域面积约752 443 km2，水面落差4480 m，蕴含着丰富的水能资源.唐乃亥水文站位于黄河上游，站前河长共1553 km，拥有200.4亿m3的多年平均径流量，占流域天然径流总量的34.2%，是黄河上游的重要水文站.该水文站为黄河的防洪抗旱、水量调度以及水能资源的开发利用提供了基本依据，为下游龙羊峡水调等重点水利工程单位提供了重要的水情信息.本文选取唐乃亥水文站1956—1997年（共42年）的径流资料，对黄河上游的径流进行频率分析，以探索年、月径流联合分布在典型年径流过程设计计算中的作用.

4.1 边缘分布

首先，建立年径流和各月径流的边缘分布.选取水文频率计算中常用的P-Ⅲ型曲线、Gumbel型曲线和对数正态分布曲线拟合样本数据，采用矩法估计分布参数.运用K-S检验方法对边缘分布的拟合优度进行检验，取显著水平α=0.05，则检验统计量的临界值Dα=0.210，若检验统计量Dn＜Dα，则认为可以接受该分布曲线；若有多个分布线型通过了K-S检验，则按照均方根误差（RMSE）和AIC值最小原则选择最优分布函数.计算结果见表2.

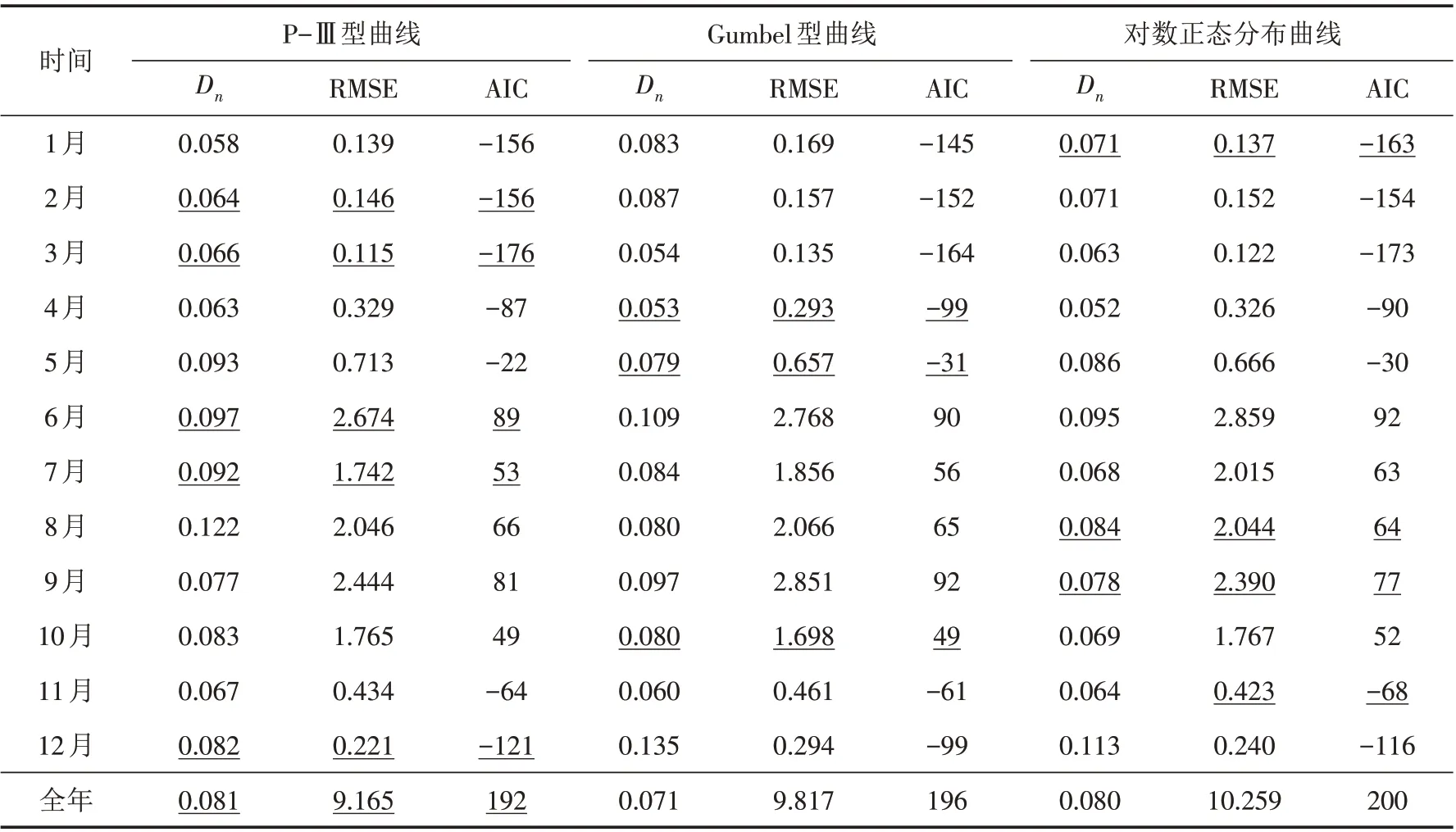
表2 径流边缘分布拟合优度检验Tab.2 Goodness of fit test of runoff marginal distribution

由表2可知，所有曲线分布的检验统计量均小于临界值0.210，都通过了K-S检验，可按照RMSE和AIC值确定最终的边缘分布.根据表2结果可知，1956—1997年这42年中，1月、8月、9月、11月的径流量服从对数正态分布，4月、5月和10月的径流量服从Gumbel分布，其他月份以及全年的径流量服从P-Ⅲ型分布.

4.2 联合分布

选择3种常见的阿基米德Copula函数模拟年、月径流的联合分布，根据样本的秩相关系数估算生成元参数θ.对生成的联合分布，采用K-S检验方法进行检验（置信水平为95%），并根据RMSE和AIC值选择最优的Copula函数，计算结果见表3.

表3 径流联合分布拟合优度检验Tab.3 Goodness of fit test of runoff joint distribution

结果表明，在95%置信水平下，初选的3种阿基米德Copula函数均通过了K-S检验.在全年与6月径流联合分布拟合结果中，Gumbel Copula函数具有最小的RMSE和AIC值，则选择Gumbel Copula为最优Copula函数；类似的，对于其他组合的径流联合分布，Frank Copula的RMSE和AIC值最小，则选择Frank Copula为最优Copula函数.图1以全年与1月的径流组合、全年与6月的径流组合为代表给出了经验联合概率和Copula理论概率的对比结果.从图1可以看出，数据点均匀、紧密地分布在45°线的左右两侧，表明选定的Copula函数具有比较好的拟合效果.

图1 经验联合概率与二维Copula理论概率对比图Fig.1 Comparison of empirical joint probability and two-dimensional Copulas theoretical probability

4.3 典型年径流过程计算

根据年、月径流的边缘分布和阿基米德Copula函数，计算得到径流的联合分布以及条件分布.取丰水年、平水年、枯水年的设计频率（超越概率）分别为25%、50%、75%，按照条件分布概率密度函数值最大原则，分别计算年径流在25%、50%和75%设计频率下，各月径流的最有可能值，从而模拟径流的年内分配，结果见表4.

表4 不同设计频率下年、月径流最有可能组合Tab.4 The most likely combination of yearly and monthly runoff under different design frequencies

取上述过程模拟的结果作为一组初设的典型年径流过程.其中，丰水年径流总量Q25%,d=225.70亿m3，而根据年径流量排频计算的结果Q25%,p=234.62亿m3，按照同倍比法对该典型年径流过程进行缩放，倍比系数K25%=Q25%,p/Q25%,d=1.040，即得丰水年径流过程；同样的，可以获得平水年、枯水年的径流过程，结果见表5.

表5 黄河上游典型年径流过程计算结果（考虑年、月径流联合分布）Tab.5 Calculation results of runoff process in the upper reaches of the Yellow River in deferent typical years（considering the combined distribution of yearly and monthly runoff）

4.4 考虑联合分布与未考虑联合分布的径流过程比较

关于典型年径流过程设计计算，传统的方法是，首先对长期实测径流资料进行频率分析，确定设计年径流量，然后选择年径流量与其最接近的实际年份为典型年，对典型年径流过程按同倍比法或者同频率法缩放得到最终的径流过程.图2 a给出了按照传统方法求得的丰水年、平水年、枯水年的径流过程.其中，4月—6月的平水年径流量比丰水年高；10月—11月的枯水年径流量比平水年高，12月的枯水年径流量比丰水年高.这是由于传统方法在选定设计典型年径流过程时，并未完全考虑到径流的年内分布，在实测历史径流资料中选取代表年时，平水年遭遇了丰水月，丰水年遭遇了枯水月，这样求得的径流过程，容易受极端月径流值的影响，使结果不具有代表性.

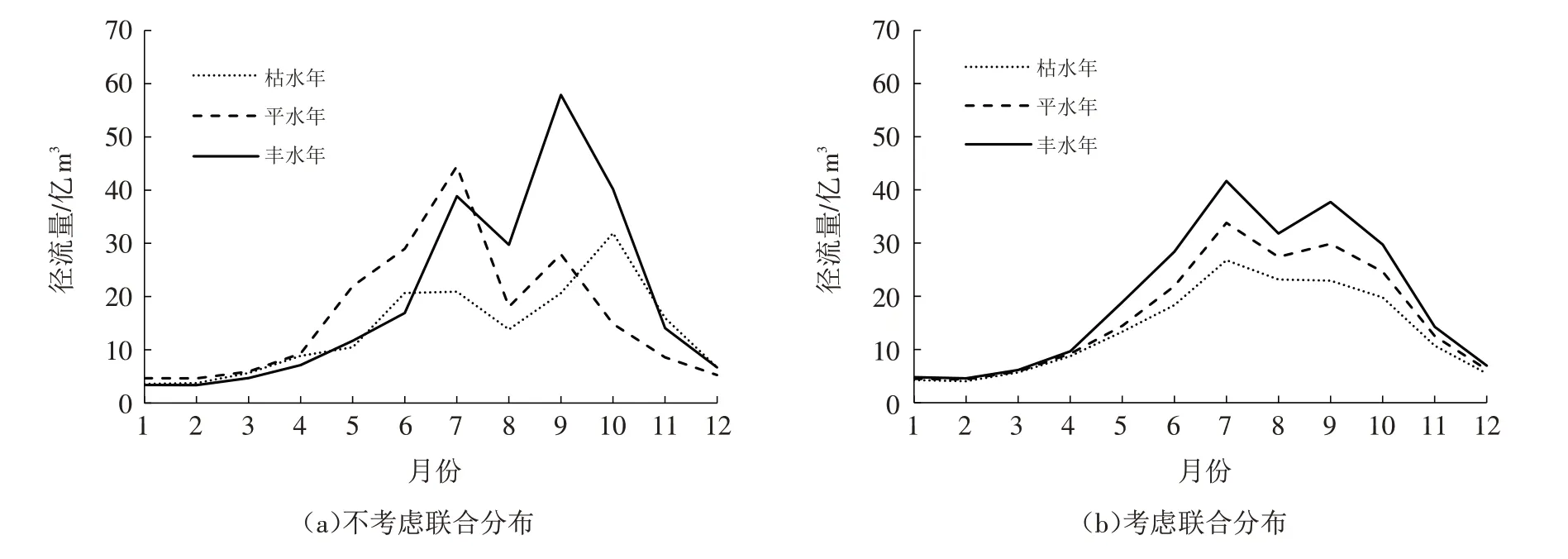
图2 黄河上游典型年的径流过程Fig.2 Runoff process in the upper reaches of the Yellow River in deferent typical years

引入年、月径流联合分布后，基于条件分布考虑年、月径流的丰枯遭遇概率，以条件最有可能径流值代替实测值，能够有效地避免极端月径流值的影响，使径流过程具有更典型的年内分布特征（如图2 b）.以枯水年为例对比两种径流过程，如表6所示，其中条件概率密度表示月径流xi相对于年径流（163.21亿m3）的条件概率密度值.由表6可以看出，考虑联合分布的各月径流条件概率密度比不考虑联合分布的各月径流条件概率密度大得多，从概率理论上来说，这代表着前者发生的可能性更大，是更容易出现的年、月径流组合.

表6 考虑联合分布与不考虑联合分布所得径流过程的对比（以枯水年为例）Tab.6 Comparison of the runoff process with and without considering the joint distribution（taking dry years for example）

另一方面，对两种方法生成的径流过程进行频率计算，得到丰水年、平水年、枯水年的年、月径流频率对比情况，结果见图3.不考虑年月径流联合分布时，各月径流频率与年径流设计频率相差较大，容易出现丰水年遭遇枯水月（图3 a中1月—6月）、枯水年遭遇丰水月（图3 c中10月—12月）的极端情况；考虑联合分布之后，丰水年1月—4月设计频率高于25%，5月—12月设计频率基本在25%上下（图3 a）；平水年5月—10月设计频率基本在50%上下，其他月份的径流频率低于50%（图3 b）；枯水年6月—10月设计频率基本在75%上下，其他月份的径流频率低于75%（图3 c）.总的来说，考虑年月径流联合分布后，各典型年下的年、月径流丰枯情况存在一定的“交叉”现象，但避免了丰水年遭遇枯水月、枯水年遭遇丰水月的极端情况；从年内过程看，各典型年下汛期的年、月径流具有较高的同频性和一致性，这是流域的季风性气候所致，降雨和径流主要发生在汛期，枯期则无明显规律.

图3 两种径流过程的年月同频情况对比Fig.3 Comparison of co-frequency between the two runoff processes

5 结论

本文针对水文典型年径流过程设计计算中的年、月径流丰枯遭遇概率问题，基于二维阿基米德Copula函数构建径流的联合分布，用条件分布概率密度函数确定了年、月径流的最有可能组合，并得到了典型年径流过程.同时，以黄河唐乃亥水文站的实测径流为例，比较了基于年、月径流联合分布的径流过程与按传统方法求得的径流过程，得出结论如下：

1）考虑联合分布的径流过程有效地减小了极端月径流值对典型年径流过程的影响，使径流的年内分布具有更加典型的丰枯特征，且三种代表年的径流过程一致性较强.

2）从年、月丰枯遭遇概率看，考虑了联合分布后，汛期径流的年、月同频性有了较大的改善，年内分布过程更具有代表性.

3）总体而言，本文基于二维阿基米德Copula函数构建的年、月径流联合分布在水文典型年径流过程的设计计算中能够产生较好的结果，该方法可以应用于其他地区的水文频率计算，为其他地区的典型年径流过程设计计算提供借鉴和参考.