基于蚁群算法的装配式建筑施工工序多目标优化模型
刘香香,孙 凤
(重庆工程学院 土木工程学院, 重庆 400056)
近几十年来,随着我国城市化进程的不断进行,建筑业经历了高速发展时期,1952年我国建筑行业产值不足100亿元,到2017年已经达到21.4万亿元,占同期国内GDP的26%,实现了几千倍的增长[1]。然而,尽管目前我国建筑业规模已经达到一定规模,但建筑行业内部仍存在着一定的问题,尤其是精细化管理程度仍然不够。例如,李锋等[2]经过研究发现,当前建筑施工过程的工期管理与成本管理亟待优化,绝大部分建筑工程面临着延期完工的风险与现状,也曾发生过成本超支现象。此外,由于建筑业属于高能耗低效益产业,长期以来产生了大量碳排放,不断加剧全球变暖现象,因此,针对建筑施工过程的碳排放控制有着重要意义[3,4]。作为一种更环保、可持续的施工方式,装配式建筑逐渐成为了建筑业的发展方向,也有学者从施工工序的角度出发对装配式建筑多目标优化进行了研究,例如,伊长生等[5]考虑了人员、技术以及天气等因素,建立了基于工序的“工期-成本-质量”多目标优化模型,并利用优化算法进行求解;罗少帅[6]将预制构件生产的工序模式划分为节约、正常与赶工模式,对预制构件的生产工序进行了优化研究。然而,目前结合碳排放因素的施工工序多目标优化研究相对较少,基于此,本文借鉴以往学者的相关研究思想,以装配式建筑中叠合板施工工序为例,在整理施工工序流程的基础上,深入分析每道工序在不同施工执行模式下所需的成本、工期以及产生的碳排放,最终通过蚁群算法进行优化求解,选择出能实现“成本-工期-碳排放”综合最优的施工方案。
1 施工流程梳理
建筑施工现场工序流程众多,从基础工程施工到竣工验收,其中的每个分项工程都包含许多细微工序。目前主要的建筑施工形式包括现浇施工与装配式施工,随着建筑业的不断发展,现浇施工已经难以满足人们对环境保护的要求,而装配式施工不仅能有效提高施工效率,还能有效降低施工过程对环境的污染[5],因此,全球许多国家都在推进装配式建筑的发展。在装配式施工模式下,每道分项工程有着相对固定的工序流程,而且施工过程的相对规范使得工序数据更加清晰、全面,所以本文选择装配式施工模式工序流程展开研究,不仅能提高研究的可行性,还能顺应建筑业发展趋势。
从目前装配式施工的实践情况来看,叠合板构件的施工过程标准化程度较高,施工过程较为规范,因此本文以叠合板构件安装为例,梳理装配式建筑叠合板构件安装工序流程,在此基础上建立多目标优化模型。
一般来说,叠合板构件的安装工序可以依次分为以下过程:构件入场及检查、架设装备支撑、基层与施工面清理、预埋件布置、叠合板吊装运输、叠合板安装就位、灌浆作业、节点保护、现场清理等流程[6,7]。同时,通过资料搜集与现场调研,能够获得每道工序的人工、材料、机械消耗,从而能进一步计算出每道工序的成本与碳排放,工序持续时间同样可以通过现场调研获取。具体来说,叠合板构件的安装工序及资源消耗情况如图1所示。
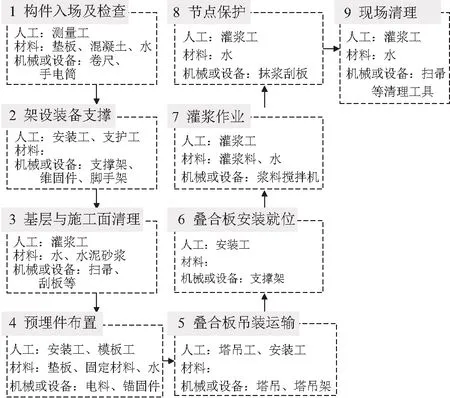
图1 叠合板构件安装工序及资源消耗情况
2 多目标优化问题
多目标优化思想起源于经济学领域,随着人们不断意识到生产资料的有限性,如何运用最少的生产资料获得最大的收益成为了学者们关注的问题。基于该思想,多目标优化过程寻求在同样产出的条件下,如何优化资源配置,使得生产过程消耗的生产资料最少。该理论最早由经济学家Patero在19世纪提出,并不断从经济学领域拓展到系统工程、建设项目、生产调度等领域[8]。对于工程项目来说,多目标优化问题表现为工期、成本、安全、碳排放乃至其他指标的综合优化,利用多目标优化的相关思想与方法,能够有效解决这一问题。
一般来说,利用数学函数转换的相关原理,多目标优化问题可以转换为数学模型,如式(1)所示。
(1)
式中:f′(x),f″(x),…代表各个子目标,每个子目标都有着相应的数学函数表达式;Tm是可行解空间,其中的每一个解都能适用于原问题,但是并非都是最优解,通常来说,只有少数几个解能使得所有目标函数相对最小;g′(x)和h′(x)分别为目标函数的约束条件,通常约束条件有多个。
在建立多目标优化模型后,下一步需要针对模型进行求解,由于多目标优化模型具有一定的特殊性,因此需要运用特殊方法进行处理,包括以下几种方法[9]:
(1)目标规划法。该方法较为简单,适用于参数少、约束少的多目标优化问题,首先寻找出每个子目标的最优值,然后将每个子目标的最优值当成原问题的约束条件。最后,缩小每个子目标与其对应最优值的差值,最终得出的最优解就是原问题的最优解。
(2)固定权重法。该方法利用权重系数衡量每个子目标对整体目标的重要性,通过0~1之间的权重系数与子目标值计算出综合函数值,最后对每个可行解对应的综合函数值进行比较,若综合函数值最优,则说明对应的可行解最优。
(3)动态权重法。与固定权重法类似,对每个子目标赋予一定权重,但该方法采用的是动态权重,每次计算过程中的权重系数都会发生变化,从而提升了求解过程的随机性和全局性,该方法适用于子目标之间较为均衡、无明显主导性的多目标优化问题。
以上三种方法是多目标优化求解过程运用最广泛的三种方法,其中,动态权重法相较于其余两种方法,有着以下优势:首先,权重系数易于操作,能快速合理地将多目标优化问题转化为单目标优化问题;其次,权重系数采用动态变化的方式,避免了求解过程中陷入局部最优,提高了优化结果的科学性;此外,该方法运用成熟,有着一定的参考经验,能与计算机语言算法实现良好的协调。因此,本文选择动态权重法对多目标优化问题进行求解,在迭代过程中,权重系数通过式(2)生成。
(2)
式中:wi为第i个子目标的权重系数,且i=1,2,3;ai为0~1之间的随机数。在每次迭代过程中,算法系统针对ai进行赋值,进而计算得出动态权重系数,进一步利用子目标函数值与权重系数计算得出综合目标函数值,实现多目标优化问题向单目标优化问题的转换。
3 优化模型建立
在装配式建筑施工现场,叠合板构件安装过程的工期、成本与碳排放取决于投入的人工、材料、机械等因素。伊长生等[5,6,10,11]研究发现,预制构件厂、装配式建筑施工现场工序可以划分为正常模式、赶工模式与节约模式进行研究,不同的执行模式对应着不同的生产资源,并耗费不同的成本、工期。在此基础上,考虑碳排放因素后,叠合板构件现场安装工序也能划分为以上三种模式,同一道工序在不同执行模式下对应着不同的成本、工期与碳排放,寻找出使得多目标最优的工序执行模式组合,便能为现场施工的优化提供指导。
3.1 现场施工数据
结合文献资料与现场调研,对叠合板构件现场安装工序施工模式进行分析,以尺寸为3150 mm×1250 mm×60 mm的叠合板构件安装施工为例,将其施工模式基本信息汇总如表1所示。

表1 叠合板构件安装工序施工模式基本信息汇总
结合表1中的数据,进一步对9道工序在不同执行模式下的成本与碳排放进行计算。其中,施工成本包括人工成本、材料成本及机械成本(如塔吊台班费等),人工成本按照45元/h进行计算,材料成本依据工序实际消耗的材料用量与市场价格进行计算,机械成本依据台班费或折旧进行计算。碳排放来源包括工人呼吸、材料及能源消耗,工人呼吸产生的碳排放由工作时间及呼吸碳排放因子进行计算,材料产生的碳排放由材料用量与材料对应的碳排放因子进行计算,而能源消耗产生的碳排放主要考虑现场使用的汽油、电能等能源,结合能源碳排放因子进行计算。本文运用的碳排放因子如表2所示,计算得出的每道工序在不同执行模式下的成本、工期与碳排放数据汇总如表3~5所示。
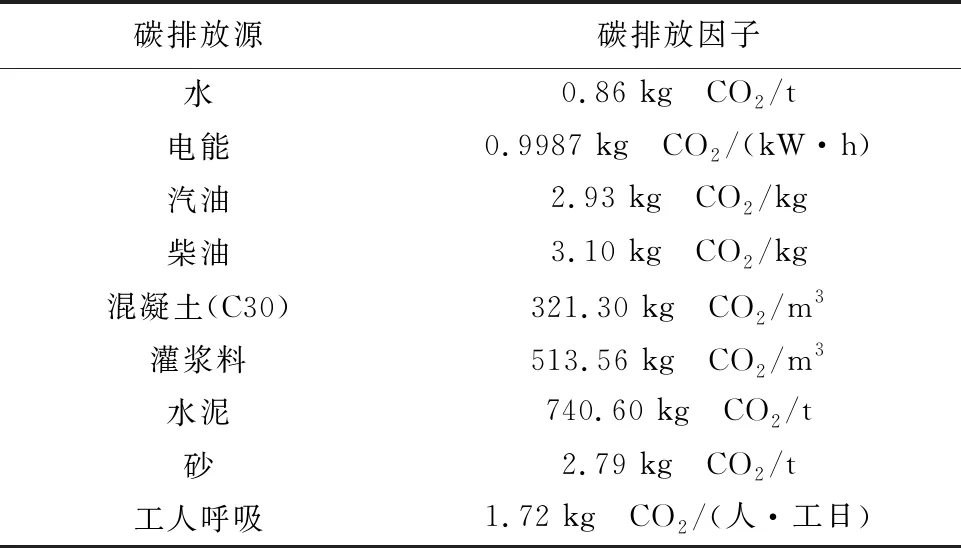
表2 碳排放因子

表3 叠合板构件安装工序成本数据汇总 元
3.2 施工优化模型
本文的优化目标为“成本C-工期T-碳排放E”的多目标优化,依据不同工序所包含的执行模式,建立优化模型如式(3)所示。
(3)
式中:m为施工工序的数量;qi为第i道工序拥有的执行模式数量;Dij为决策变量,取值为0或1,当第i道工序采用第j种执行模式时,其取值为1,反之则为0。
4 蚁群算法流程
由于多目标优化问题求解过程涉及到复杂的数学模型,依靠人力难以计算,因此需要借助计算机算法进行实现。依据算法特点,当前多目标优化问题研究领域的算法包括精确算法与启发式算法两大类。精确算法适用于规模较小、参数较少的多目标优化问题,一般能得出原问题的唯一最优解,但缺点是消耗的时间较长,该种求解算法包括分支定界法、割平面法以及整数规划法等[12]。随着多目标优化问题的不断复杂化以及计算机技术的不断发展,启发式算法得以涌现,包括蚁群算法、模拟退火算法、禁忌搜索算法、遗传算法等常见方法[13],该类算法适用于规模较大、参数较多、难以找到最优解或最优解不唯一的复杂多目标优化问题,通过反复迭代不断逼近最优解,最终得出原问题的最优解集。由于蚁群算法具有良好的普适性、可操作性与鲁棒性,适用于中等复杂程度的多目标优化问题,因此,本文选择蚁群算法对施工工序多目标优化模型进行求解。具体来说,本文蚁群算法包括以下步骤:
步骤1:变量定义。蚁群算法迭代过程中包括许多重要参数,用以控制算法的迭代过程,包括循环次数N、蚂蚁数量m、信息素重要程度α、启发性因子重要度β、信息素强度Q、信息素挥发率p等参数。其中,N取决于原问题的规模,通常情况取值在200~500之间,本研究中问题规模较小,但为了确保优化效果,取N=300;蚂蚁数量影响着算法的收敛速度,依据经验做法,取m=20;α与β影响着算法过程的随机性,为了确保算法的随机性同时兼顾算法运行效率,取α=1.15,β=0.8;Q与p的设置是为了避免算法陷入局部最优,依据经验做法,取Q=10,p=0.3。
步骤2:初始可行解。作为算法的起始,需要随机产生一组满足约束条件的可行解,即生成20只蚂蚁,其中每只蚂蚁表示一个可行解,其所代表的的可行解对应的工期、成本与碳排放不完全相同。
步骤3:产生权重系数并计算综合目标函数值。依据式(2)针对每个子目标函数随机生成权重系数,并计算综合目标函数值F。当F越小,表明对应可行解的工期、成本与碳排放越小,该可行解就越优。
步骤4:信息素更新。依据信息素强度以及每只蚂蚁对应的综合目标函数值计算每一条路径上蚂蚁经过时留下的信息素浓度,即Q/F。此外,每条路径上的信息素浓度等于此次循环开始前的信息素保留值与此次循环过程中蚂蚁释放的信息素之和。
步骤5:判断蚂蚁的路径选择。当路径上的信息素浓度越大,蚂蚁选择该路径的概率则越高,依据此原理,分别对蚂蚁选择每条路径的概率进行计算。
步骤6:为蚂蚁选择路径。依据蚂蚁选择每条路径的概率,随机分配蚂蚁的路径选择,并记录蚂蚁在经历一次循环后的路径选择与综合目标函数值。
步骤7:重复上述循环过程,直到循环次数达到300次。
步骤8:寻找最优解。循环次数达到预设值后,在生成的解集中寻找相对最优解,从而确定原问题的全域最优解。由于初步循环得出的解均为相应领域内的最优解,而非全域最优解,因此需要针对每个解进行比较,从而筛选出全域最优解。
具体算法流程如图2所示。
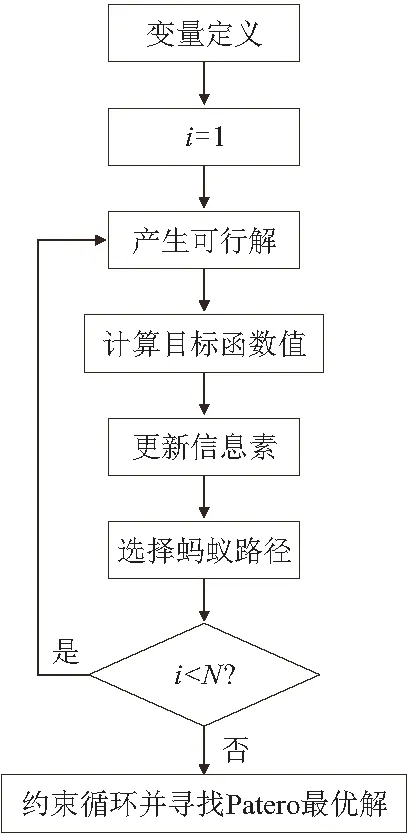
图2 蚂蚁算法流程
5 优化结果
利用计算机编程实现蚁群算法,最终得出5个相对最优解如表6所示,这些解构成了原问题的最优解集。同时,算法还能得出每个可行解对应的工序施工模式,如表7所示,从该表中可以得出对应最优可行解的工序模式选择,从而能有效指导施工过程。

表6 原问题最优解集
由表6可以看出,经过优化后的叠合板安装工序,其可行解的成本平均值为160.96元,工期平均值为65.60 min,产生的碳排放为19.64 kg。而优化前,若所有工序都在正常模式下执行,其成本为163.5元,工期为68 min,产生的碳排放为21.2 kg。因此,优化后该叠合板构件安装过程成本降低了1.55%,工期降低了3.52%,碳排放降低了7.36%。

表7 最优解对应的工序模式
6 结 论
随着人们对碳排放的不断关注,作为碳排放大户,建筑业面临着碳排放优化的重要任务。相较于传统式建筑,近年被广泛推行的装配式建筑有着更好的环境友好性,许多学者也针对装配式建筑的成本、工期与碳排放等方面进行了研究。在以往研究的基础上,本文综合考虑了装配式建筑施工阶段的成本、工期与碳排放多目标优化,并力求通过工序施工模式的合理选择,从微观层面实现施工过程的多目标优化。在研究过程中,本文以叠合板构件安装过程为例,首先梳理施工工序流程,并将工序分为正常、赶工、节约三种执行模式,在不同执行模式下,每道工序有着不同的成本、工期与碳排放,在此基础上,构建了多目标优化模型,并利用蚁群算法进行求解,最终得出的优化结果降低了1.55%的成本、3.52%的工期以及7.36%的碳排放,同时,算法还得出了每个最优解对应的工序模式选择情况,从而能对施工过程提供更多指导。
未来,该优化思路与方法能运用于施工现场更多工序流程的优化,从而进一步实现整个施工现场的整体优化。

