卫星轨道标准化的计算方法比较

夏志浩

(常州市金坛区测绘地理信息院，江苏 常州 213200)

随着社会的发展，特别是无人机、无人驾驶等一些新兴领域都对定位精度提出了更高的要求。无论是GNSS控制网还是精密单点定位的解算，精密星历的使用都对轨道误差的减小有着积极的作用[1-2]。为了提高卫星的定轨精度，通常采用IGS 提供的精密星历。精密星历分为最终星历(IGF)、快速星历(IGR)、超快速星历(IGU)三种星历[3]。本文采用的是15 min采样间隔的最终星历，实际解算中需对其进行插值或者拟合。其中较为常用的方法就是拉格朗日多项式插值法[4-5]和牛顿多项式插值法[6]，有一些学者也提到了内维尔逐次线性插值法[7]和切比雪夫多项式拟合法[8]。

在本文中，笔者使用拉格朗日插值和切比雪夫多项式拟合两种方法对15 min采样间隔的最终精密星历进行了标准化，并进行分析对比。

1 卫星轨道标准化模型

1.1 拉格朗日插值法

假设函数f(x)在一系列点xi(称之为节点)上精确值为已知，用一简单函数y(x)逼近f(x),要求在节点y(x)与f(x)有相同的函数值，这就是插值。拉格朗日插值函数如下[9]：

(1)

式中，lj(x)称为拉格朗日插值基函数，即：

lj=

(2)

当n=1时，L1(x)称为线性插值，它可以表示为：

(3)

当n=2时，L2(x)称为抛物线插值，它可以表示为：

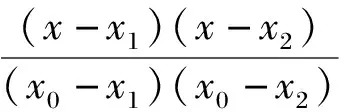
(4)

在精密星历内插时，xi为精密星历中的时间参数，f(x)为相对应的卫星位置和卫星钟差数据。因为被插值点位于所有节点的中间位置精度最高，所以在本文中所有被求解节点都位于中间位置，即对待求历元的卫星位置和钟差进行插值时，前后所取的历元数据个数相等。

1.2 切比雪夫多项式法

切比雪夫多项式拟合就是根据给定的数据拟合出一个函数，使其在给定点的函数值与给定值之间的方差和最小[10]。假设需要在时间间隔[t0,t0+Δt]计算n阶切比雪夫多项式系数：

B=

(5)

(6)

式中，n为切比雪夫多项式的阶数；CXi、CYi、CZi分别为X坐标分量、Y坐标分量、Z坐标分量的切比雪夫多项式系数。

在切比雪夫多项式中根据如下递归公式确定Ti：

T0(τ)=1,T1(τ)=1，Tn(τ)=2τTn-1(τ)-Tn-2(τ); |τ|≤1,n≥2

(7)

设Xk为观测值，则误差方程为：

(8)

误差方程的矩阵展开式如下：

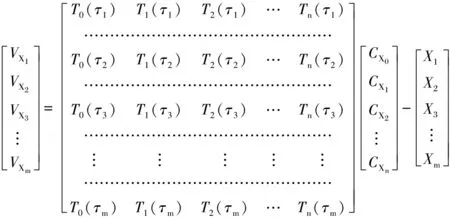
(9)

令V=[VX1VX2VX3…VXm]T;

L=[X1X2X3…Xm]T。

2 算例及结果比较

在本实验中，笔者使用的数据为2012年1月4日的IGS最终精密星历(esa16693.sp3)，从0 时0 分至23 时45 分，共96 个历元。首先对G01、G02、G03三颗卫星分别进行6～35阶拉格朗日插值和9～25阶切比雪夫多项式拟合，求取2012年1月4日12时0分0秒卫星的坐标，再将其与该历元已知卫星坐标取差值，以X方向为例，结果如图1和图2所示。

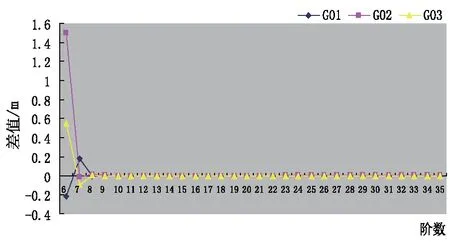
图1 拉格朗日插值结果

图2 切比雪夫多项式拟合结果

由图1可知，拉格朗日插值在阶数取到9时，卫星插值的结果趋向稳定，与已知的卫星坐标基本相等，当拉格朗日插值阶数取到35时，卫星坐标的差值也不是很大，没有见到明显的龙格现象。由图2可知，当切比雪夫多项式的阶数取到11阶时，卫星坐标的差值趋于稳定，直到拟合到第22阶多项式时，卫星坐标的差值开始增大，拟合出的卫星坐标开始偏离卫星坐标的真实值，出现龙格现象。因此在卫星轨道标准化时应充分考虑卫星星历的数据量，在保证精度和效率的情况下，尽量避免使用高次插值或拟合。

通过以上结果的分析，在该样本中拉格朗日插值取9～11阶，切比雪夫多项式拟合阶数取12～14，计算结果精度和效率最优。下面以10阶拉格朗日插值和13阶切比雪夫多项式为例，分别计算32号卫星于12时0分0秒到12时1分0秒时间间隔的卫星坐标(采样间隔为1 s)，结果如图3所示。

图3 两种方法计算的卫星坐标差

从结果可以看出，卫星坐标之差在X、Y方向基本在30 mm以内，在Z方向基本在40 mm以内。随着历元数的增加，卫星坐标之差在0 mm上下摆动。从该时间段中选取前6个历元，计算结果如表1所示，从表中可以看出,无论是插值还是拟合方法计算出的卫星坐标差值都很小，基本在0 mm上下摆动，卫星位置坐标值稳定性相对较高。

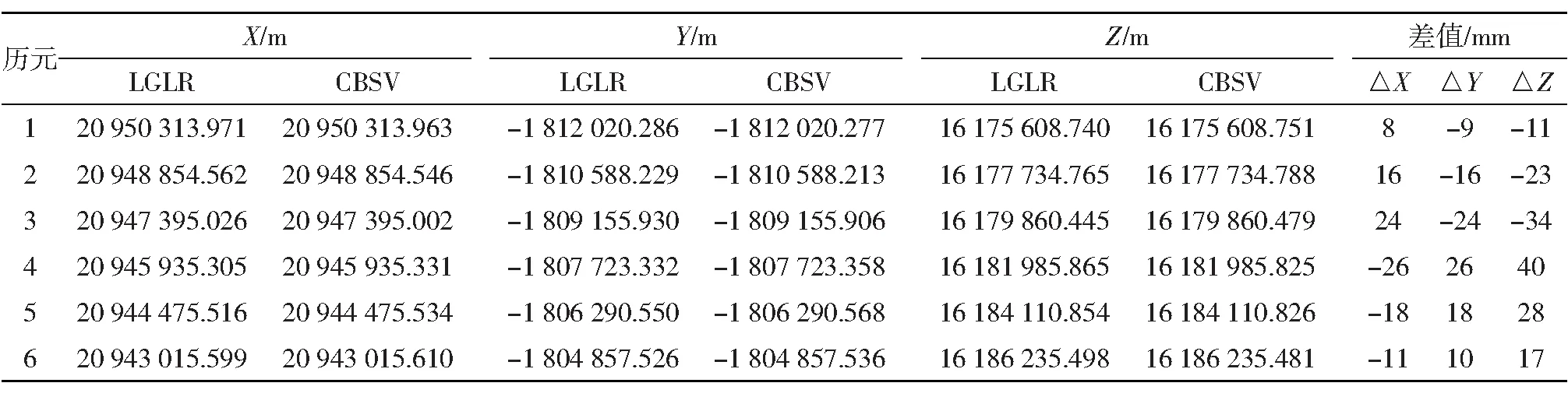
表1 两种方法计算的G32的坐标(LGLR：拉格朗日 CBSV：切比雪夫多项式)

3 结 论

通过对拉格朗日插值和切比雪夫多项式拟合结果分析：(1)拉格朗日插值法、切比雪夫多项式法只要使用的阶数合适，计算出的卫星坐标都满足精度的要求；(2)对于切比雪夫多项式法而言，多项式的阶数对结果的影响较为明显，高阶容易产生龙格现象；(3)在实际应用中，不同计算方法的效率也不一样。当求解卫星位置较少时，由于拉格朗日插值法不需要事先拟合卫星轨道，所以计算速度优势比较明显；当求解卫星位置较多时，由于切比雪夫多项式在每次计算卫星坐标时只需要代入系数矩阵，比起拉格朗日插值大量的进行插值计算效率要高很多。