采煤沉陷回填区注浆扩散分析及应用研究*

赵立钦，韩科明，李学良，贾林刚

(1.中煤科工生态环境科技有限公司，北京 100013；2.天地科技股份有限公司，北京 100013；3.中国煤炭科工集团有限公司，北京 100013；4.中煤科工集团北京土地整治与生态修复科技研究院有限公司，北京 100013)

地下煤炭资源的开采造成地表出现宽度不同的裂缝及大规模盆地式下沉，造成地表移动变形，严重影响土地开发与利用，为改善破坏土地利用情况，多采用回填的措施修整受采动破坏的土地。但由于回填土夯实程度不够，其对建(构)筑物的承载能力达不到要求，回填土的缓慢压缩会造成地表建(构)筑物变形，因此，在利用回填区前需要对其进行注浆加固处理。对回填区孔隙注浆加固效果影响最大的主要因素有注浆压力、回填土渗透性，因此，针对孔隙注浆，众多学者对此进行了详细研究。

湛铠瑜[1]基于工程实际，研发出单一裂隙动水注浆模型试验系统，将裂隙开度、粗糙度及水流作为变量，得出浆液动水条件扩散规律，并得出渗透压力的变化情况；阮文军[2]基于浆液扩散试验系统，研究浆液在裂隙岩体中运移扩散过程受注浆材料粘度的影响；李华茂[3]研制单一裂隙椭圆形注浆实验模拟平台，基于正交实验研究注浆压力、水灰比、注浆时间等因素对注浆效果的影响；张忠苗[4]自主研发模拟注浆实验装置，开展黏土压密注浆及劈裂注浆的模拟试验。

科学研究目前主要有数值模拟、理论分析、试验研究三种重要手段。数值模拟可以直观、细致地分析实验过程，并能够连续动态揭示事物演变过程，从而得到广泛应用，数值模拟在注浆模型试验研究中越来越受到重视。郝哲等[5]采用特定方法生成随机裂隙网络，并研究其浆液扩散规律；罗平平[6]通过搭建岩体裂隙网络变形耦合模型，并结合光滑裂隙内宾汉流体的流动方程研发相关应用程序；杨米加[7]基于岩体裂隙网络推导非牛顿流体渗流方程；吴顺川[8]借助离散元数值模拟，从微观上研究土体注浆过程。

以上研究都是理论分析与实验研究等方法定性分析注浆的扩散特性及规律，为浆液扩散特性的研究奠定了一定的基础。本文在上述研究的基础上，采用数值模拟的方法定量分析注浆扩散半径及其变化规律，并结合工程实践对模拟结果进行验证，取得良好的采煤沉陷回填区治理效果。为以后类似工程的实践应用提供一定的研究基础。

1 注浆扩散理论基础

针对注浆渗透扩散理论方面，相关学者已经做了大量的研究工作。Maag[9]基于浆液在理想介质中流动时按球形扩散的假设，推导出牛顿型浆液在砂土中的渗透公式：

(1)

式中，R为浆液扩散半径；r0为注浆管半径；k为渗透系数；h0为注浆压力水头；β为浆液黏度与水黏度的比值；t为注浆时间；n为砂土的孔隙率。

刘嘉材[10]采用室内实验模拟浆液在裂隙中的扩散过程，研究牛顿流体在二维光滑裂隙中的运动规律，推导出注浆时间与扩散半径的表达式：

(2)

式中，R为浆液扩散半径；P0为受灌裂缝内地下水压力；P为灌浆孔内压力；T为灌浆时间；r0为灌浆孔半径；b为裂缝宽度；η为浆液黏度。

杨晓东[11]根据宾汉流体在裂隙中的运动规律，弱化浆液在裂隙中流动的惯性和重力，推导出浆液的流动特性方程：

(3)

式中，P为作用于浆液微单元体上的灌浆压力；τB为裂隙中浆液流动时呈塞流运动中的切力；P0为裂隙入口处压力；h为裂隙开度；r0为钻孔半径；r为浆液扩散半径；Q为灌浆流量；η为浆液塑性黏度。

杨秀竹[12]等推导出了砂土中采用宾汉流体进行渗透注浆时，浆液扩散半径的计算公式：

(4)

式中，Δp为注浆压力差；β为浆液黏度与水黏度的比值；φ为砂砾石土孔隙率；t为注浆时间；l1为浆液最终扩散半径；l0为注浆管半径；λ为启动压力梯度。

依据上述浆液扩散理论计算所得注浆半径存在不同程度的差异，难以直接指导生产实践。因此，本文以注浆工程的应用实际为基础，采用牛顿流体型浆液在砂土体中渗透作为本次数值模拟的理论模型，并借助一定的数学工具定量研究不同注浆压力和砂土体渗透对浆液扩散半径的影响。

2 孔隙注浆扩散半径实验研究

基于以上牛顿流体在砂土体中渗透理论，为研究不同注浆压力、回填土渗透性组合条件下，注浆扩散半径的变化规律，采用离散元数值模拟进行流固耦合分析，研究组合条件作用下，浆液扩散半径的变化规律，如表1所示。

表1 数值模拟组合实验设计及实验结果

2.1 注浆压力影响分析

如图1所示，通过对比分析第一组到第四组相似模拟实验结果可以看出，当目标层位渗透系数不变的情况下，注浆扩散半径随着注浆压力的增加非线性增大。如图2所示，随着注浆压力的增大，注浆扩散半径的增加幅度逐渐减小，通过曲线的增长趋势可以看出，当注浆压力增大到一定程度时，注浆扩散半径不再随着注浆压力的增大而增大。

图1 注浆压力影响成果图

图2 扩散半径随注浆压力变化曲线

2.2 渗透系数影响分析

如图3所示，通过对比分析第四组到第七组相似模拟实验结果可以看出，当注浆压力不变的情况下，注浆扩散半径随着目标层渗透系数的增加非线性增大。如图4所示，随着目标层渗透系数的增大，注浆扩散半径的增加幅度逐渐增大，通过曲线的增长趋势可以看出，当渗透系数增加到无限大时，这与流体在没有摩擦力的地面流动的原理相似，在理想情况下，注浆扩散半径随着目标层渗透系数的增大无限增大。

图3 渗透系数影响成果图

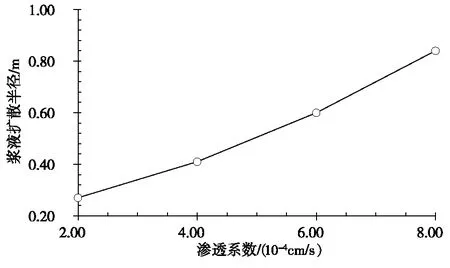
图4 扩散半径随渗透系数变化曲线

2.3 浆液扩散时效性分析

以第四组为例，分析单孔注浆扩散半径随注浆时间的变化规律，如图5所示，随着注浆时间的增加，注浆半径逐渐扩大，单孔注浆半径的增长速度逐渐变小，最后稳定到某一定值不再变化，这也就说明注浆半径的扩散具有一定时效性，受注浆压力和目标层渗透系数及浆液属性等因素的影响，不会无限增大，因此，合理掌握单孔注浆时间对于高效注浆具有一定的指导意义。

图5 扩散半径随注浆时间变化曲线

2.4 注浆半径回归分析

为定量研究注浆扩散半径与渗透系数、注浆压力之间的关系，利用数值模拟数据作为自变量与因变量值，采用二元回归分析的方法得出注浆半径与渗透系数、注浆压力之间函数关系，设置注浆半径预计公式的自定义函数形式为R=b0+b1P+b2k，式中，b0、b1、b2均为回归系数，P为注浆压力，k为渗透系数，R为注浆半径。

通过OriginLab数值拟合求得参数，b0=-0.593、b1=0.312、b2=1 019.643，由此可以得出，注浆半径预计公式为：

R=-0.593+0.312P+1 019.643k

(5)

同时得出复相关系数为0.982 9，表明该预计公式中自变量与因变量之间的关系为高度正相关；标准误差为0.048 8，说明拟合程度较好；显著性统计量为0.000 2，远小于显著性水平0.05，说明该预计公式回归效果显著。

3 工程实例分析

某光伏基地升压站坐落在采煤沉陷回填区，地貌属低中山区。场区地势北高南低，由于采煤沉陷区的回填，形成了数个高度不一、形状面积大小各异的台阶地，升压站生产区出现了架构沉降倾斜的现象，为此该升压站进行过两次采空区深部空洞注浆，由于该处理方法忽略了回填区的回填物密实度不足的问题，站内又出现部分建(构)筑物发生沉降现象。为保证升压站内建(构)筑物不受地表变形影响，对该区域再次进行回填区孔隙注浆治理。

3.1 钻孔布设方案

为保证注浆工程的有效性和经济性，结合数值模拟结果和预注浆实验，注浆压力定为2 Mpa，通过现场回填区土体渗透系数实测可知，渗透系数为7.42×10-4cm/s，由注浆半径回归计算公式可以得出其注浆半径为0.79 m，根据该参数设计注浆孔间距为1.5 m，如图6所示。

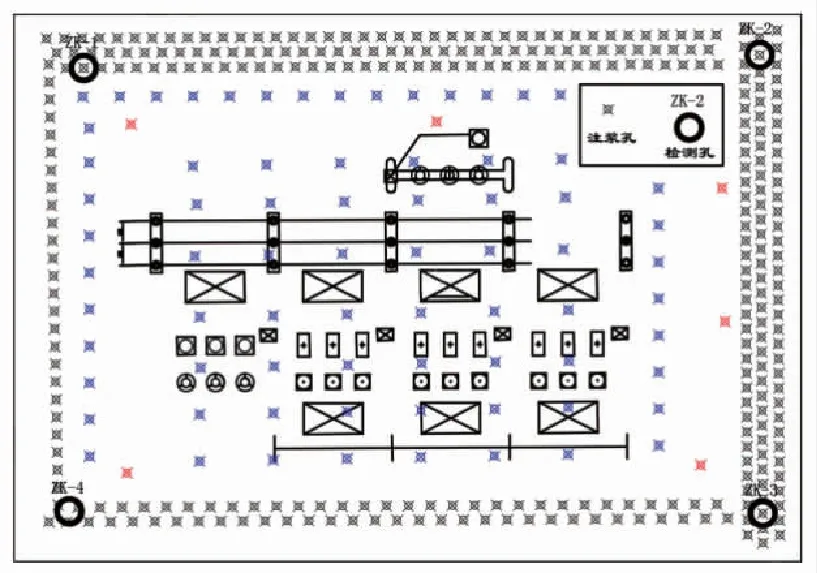
图6 钻孔分布图

3.2 注浆效果分析

为验证注浆效果，在升压站场区的四角布设四个注浆效果验证区，注浆钻孔位置如图6所示。四个方位的四组验证钻孔主要检测浅部注浆的浆液是否扩散至构架区边界，并检测浆液沿着地层裂隙的流动情况。如图7所示，检测钻孔采取岩芯中水泥结块含量较多，并且在钻探过程中孔内无漏水的现象，证明浅部注浆已经将岩层裂隙全部注满，达到预期的治理效果。

图7 检测孔岩芯

4 结 论

(1)注浆扩散半径与注浆压力呈非线性正相关，且随注浆压力增大注浆半径趋于某一定值；注浆扩散半径与渗透系数呈非线性正相关，且注浆半径增长率随渗透系数增大逐渐增大。

(2)注浆初期浆液扩散较快，而后逐渐趋近于某一固定范围，说明注浆具有一定的时效性。

(3)根据模拟实验结果进行回归分析，得出注浆半径计算公式，并将其运用到采煤沉陷区治理工程中，合理配置注浆参数，达到预期的治理效果。