B2 O3 含 量对SiO2 -Al2 O3 -B2 O3-RO体系玻璃的性能和微观结构的影响

徐言超 姚树峰 史建军

（泰山玻璃纤维有限公司 泰安 271000）

0 引言

SiO2- Al2O3- B2O3-RO 体系的玻璃是生产玻璃纤维最常用的玻璃体系之一；也是电子级玻璃纤维的基础玻璃体系。电子级玻璃纤维广泛应用于印制电路板和雷达天线罩等对介电、滤波等要求较高的产品的制造。近年来，随着电子器件和电子产品体积的减小，要求印刷电路具有更高的器件密度、更快的信号速度和更高的可靠性，这就要求印刷电路板要有更低的介电常数。作为印刷电路板主要组成部分的电子玻璃纤维是影响印刷电路板介电常数的主要因素之一。进一步降低玻璃纤维的介电常数就尤为重要和迫切［1］。

目前被广泛应用于印刷电路板的E玻璃纤维就是由SiO2- Al2O3- B2O3-RO 系统的玻璃拉制而成。其介电常数e为6.6～7.1。研究表明，该玻璃体系可以获得较低的介电常数和介电损耗［1］。在该体系中，当B2O3的 比例较高，特别是B2O3的比例达到20%（质量分数）以上时，可以得到介电常数较低的玻璃。B2O3在玻璃中是典型的网状形成体，广泛应用于各种玻璃制品中。B2O3的引入可以改善玻璃的性能。少量的B2O3可以显著提高平板玻璃、电子管玻璃等部分玻璃产品的性能［2,3］。

一些学者对二元和三元体系玻璃的性能进行了广泛的研究，但对更复杂的玻璃系统基础研究较少。本文旨在对B2O3的 含量变化时对SiO2-Al2O3- B2O3-RO玻璃体系性能的的影响进行研究探索。

1 试验

根据现有的研究数据［1］和前期试验，选择表1的玻璃组成作为本试验的基础组分。

表1 基础玻璃成分

在该基础成分的基础上，通过B2O3逐步替代其他成分，将B2O3的含量由20.0%增加到28.0%，并保持其他成分的比例不变，使其他成分的总含量由80.0%下降到72.0%。然后，考虑各种成分的影响，增加B2O3的 含量，取代Al2O3和 RO，保留SiO2为基础成分含量不变，设计出高硼玻璃成分，硼含量达到28.5%～33.5%，RO含量≤5.0%。玻璃的制备是通过按配方计算、称量好的适量的矿物原料充分混合后放置在铂金坩埚内在马弗炉中1550℃高温下充分熔化澄清，然后将熔体倒入一个预热到640～700 ℃的不锈钢模具中退火，获得一块澄清良好的透明玻璃块。

为了进行电学性能测量，将玻璃块切割并抛光制备成长×宽约为20 mm×20 mm、厚度约为1 mm的薄片，两面均匀涂覆银电极。

FTIR分析采用Mattson 5020系统，记录了4000～400 cm-1范围内的傅里叶变换红外吸收光谱。

2 结果和讨论

为便于描述，不同试样按照表2对应的编号代替。

表2 不同样品对应的编号

试样5 退火后浇注在金属模具上出现微小的分相玻璃条纹，其他样品均形成透明均匀的非晶态玻璃熔块。所得玻璃进行XRD图谱分析显示，所有制备的试样均为典型的非晶态。

2.1 介电性能

图1为不同试样介电常数的变化趋势。

图1 不同试样的介电常数

图2 各试样在不同频率下的介电常数

介电常数e和介电损耗tand随玻璃中B2O3含量的增加而减小。试样1～5中，B2O3逐渐增加，其他成分比值固定，e由5.02减小到4.89，降低了2.59%，且变化越来越慢，介电损耗tand由26×10-4减 小到17×10-4，降低了34.61%。试样6在保持SiO2为基础成分不变的情况下，减少了Al2O3和RO，代之以增加B2O3，介电常数e为4.22，介电损耗tand达到了8.5×10-4，较基础玻璃分别降低15.94%和67.31%。各试样的介电常数均随检测频率的增加而变化。随着B2O3含量的增加，检测频率对其影响越来越小（图2中1～5）。

介电常数与材料的极化率直接相关，因此介电常数取决于材料的的化学结构［4］。介电特性是由电子、离子和空间电荷极化作用决定的［5,6］。其中空间电荷极化取决于玻璃的纯度和均匀性。随着硼含量的改变，形成玻璃的网络结构单元和排列也随之变化，从而导致玻璃的介电性能的变化。B3+离子在玻璃中的极化率最小，因此，随着B2O3的加入，试样的介电常数逐渐降低。

2.2 玻璃失透分析

研究B2O3对玻璃分相温度范围的影响，各样品分相温度区间如图3所示。随着玻璃中B2O3含量的增加，玻璃的失透温度范围增大，特别是样品5和6的失透温度范围较其他样品明显增大，且样品6在较高的温度区间更易发生失透，这也直接与其熔制温度较高有关。

图3 各样品失透温度范围

对失透后的玻璃XRD分析图谱如图4所示。样品6的图谱显示其失透后存在少量晶体。在梯温炉中热处理后的1～5样品的XRD图谱均为典型的非晶态。样品6的失透玻璃样品的XRD检测图谱中的衍射峰特征值与2（Al2O3） B2O3晶体的特征值相吻合。结合玻璃成分和比对晶体成分可以推断可能有少量硼铝石晶体形成。

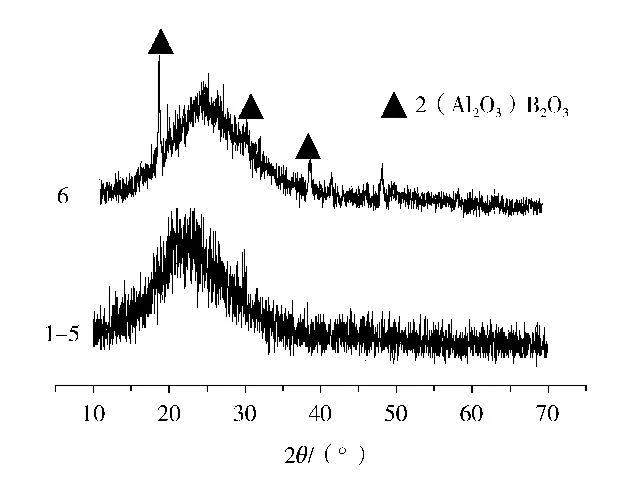
图4 各样品失透后的XRD分析

在该玻璃体系中，增加B2O3会使化合物对O2-发生剧烈的争夺，因此B2O3持续增加促进了玻璃的分相，特别是样品6在高温区域发生失透与可提供较多游离态O2-的Al2O3和CaO含量的大幅度降低有关。

2.3 SEM分析

由于样品6热处理前后的典型变化，选取其热处理前后的样品进行SEM观察，发现热处理前其呈均匀玻璃态，而在热处理后有亮色液滴状聚集，与XRD分析结论吻合，如图5和图6所示。这主要是由于玻璃相分离造成的，某些化合积聚能力比较强，在合适的温度下就会产生积聚从而使成分变得不再均一，形成这种液体状聚集体，结合XRD分析可知其中也形成了小部分析晶。

该体系玻璃中，在碱金属含量比较少时，电场强度较大的网络外体离子（如Li+，Mg2+，Ti4+等），容易在结构中产生局部积聚作用而造成分相和析晶［6］。在该玻璃中，由于碱金属离子含量很少，网络结构连接程度比较大，可以形成稳定透明的玻璃。由于B2O3、CaO、MgO的存在，在长时间的保温下一定的温度区间内会有相分离的趋势并形成析晶。

图5 热处理前样品6的SEM

图6 热处理后样品6的SEM

2.4 红外光谱分析（FTIR）

样品1～6玻璃的红外光谱（图7）显示存在五组主要峰波段：①3250～3600 cm-1区域；②1300～1450 cm-1区 域；③1050～1150 cm-1区域；④700～800 cm-1区 域；⑤400～500 cm-1区域。第一组谱带归属于解离OH-离子或H2O的反对称拉伸弛豫振动，在这组波段中各样品没有明显的差异。1090 cm-1的宽频带是由Si-O-Si的拉伸弛豫振动引起的，这组波段的位置是由Si-O-Si的键角决定的，键角扩大后，波段向高频移动，相反，波段向低频移动。

图7 各样品的红外光谱分析

从图7可以看出，不同样品的第①（3250～3600 cm-1）区域的吸收峰的位置变化不大，表明所有样品的Si-O-Si链没有明显变化。而④（700～800 cm-1）区域是由于［AlO4］单元的Al-OAl键的伸缩振动产生的，⑤（400～500 cm-1）区域的出现是由于Si-O-Si键在硅酸盐网络中的弯曲振动产生的。不同样品在④（700～800 cm-1）区域和⑤（400～500 cm-1）区域的吸收峰没有较明显差异，也就是说Al-O-Al和Si-O-Si的吸收光谱基本一致，说明不同样品的Si和Al的能带结构是相对稳定的。而②（1300～1450 cm-1）区域的吸光度谱是由O-B-O在二硼酸基、三硼酸基、四硼酸基中的反对称拉伸弛豫振动引起的［7］。在②（1300～1450 cm-1）区域，样品1～5的红外光谱吸收峰基本一致，而样品6的吸光光谱向低波数略有偏移而使该处吸收谷略有变宽，这是由于随着B2O3含量的增加，玻璃中会形成二硼酸基团和四硼酸基团。其中BO3与BO4直接相连，其中BO3中的B-O键更强大，这种连接导致了BO3中BO键的弱化，从而导致了这种光谱的偏移［7］。所有样品的红外光谱在920 cm-1处出现一个较弱的波段，这是由于BO4中孤立的B=O基团的振动和非桥接氧在不同基团中震动引起的。从样品1～6该波段的强度逐渐增大，表明了B2O3浓度的增加加剧了各离子对O2-的争夺，导致非桥氧的增加。

3 结论

（1）介电常数e和介电损耗tand随着B2O3含量的增加而逐渐减小。在样品1～5中，介电常数e随着B2O3含量的增加下降相对较缓慢，而介电损耗tand下降趋势更加明显。

（2）随着玻璃中B2O3含量的增加，玻璃失透温度范围增大，玻璃失透是由分相引起的。试样6的失透温度范围最大，并趋向于高温区，除样品6中有少量针状晶体外，其他失透玻璃中未发现晶体。

（3）SiO2- Al2O3- B2O3-RO玻璃具有复杂的组合体，是网络形成剂、中间体和改性体的混合存在。红外光谱分析表明，B2O3含量的增加导致sp2平面的BO3转化为更稳定的sp3平面的四面体BO4，并可能产生非桥氧。每个BO4单元与两个这样的其他单元连接，每个单元的一个氧与另一个离子连接，这种结构导致了长四面体链的形成。