双联合收发空间调制方案设计与性能分析

卜祥燕, 白智全，*, 庞 珂, 郝新红, 马丕明, 孙 健

(1. 山东大学信息科学与工程学院, 山东 青岛 266237; 2. 北京理工大学机电学院, 北京 100081)

0 引 言

作为一种特殊形式的多输入多输出(multiple input multiple output,MIMO)技术,空间调制(spatial modulation,SM)技术已被广泛关注和研究[1-4]。与传统MIMO技术相比,典型SM系统在发送端仅激活一根发送天线,并利用空间域中的天线位置来传输信息比特。因此,其可消除MIMO系统中天线间同步和信道间干扰的问题,降低接收端检测复杂度,并改善系统频谱效率。为进一步提升SM系统的频谱效率,广义空间调制(generalized spatial modulation,GSM)技术得到广泛研究[5-6]。在GSM系统中,待传输信息比特可选择激活发送天线的组合,并发射相同或多个独立的星座符号来提高频谱效率。而正交空间调制[7-8](orthogonal spatial modulation,QSM)作为一种新的高效SM技术,其在发送端激活两根发送天线,分别发送调制符号的实部和虚部。由于传输符号实部和虚部的载波是正交的,可以有效避免信道间干扰,提高系统频谱效率及传输性能。

对于上述SM技术及其扩展技术研究,均是利用发送天线索引来携带额外信息,以提高频谱效率。而预编码空间调制(precoding-aided spatial modulation,PSM)技术及其拓展技术[9-12]则是将SM的概念应用于接收端,利用发送信息比特在接收端激活一根接收天线或接收天线组合进行信息接收,简化了接收端结构,提供了更多的空间信息,在提高频谱效率的同时,实现了更优的系统性能。文献[13]研究了采用联合最优检测和解耦次最优检测的广义PSM(generalized PSM,GPSM)系统的容量和错误率。由于线性预编码的应用,传统的PSM方案往往只适用于对称或欠定系统。文献[14]提出了一种基于分组PSM(group PSM)技术,其适用于超定系统,也适用于接收天线数大于发送天线数的情况,主要原理是将接收天线均分成若干组,利用额外的信息比特选择其中一组接收信息,提高了PSM的可伸缩性。针对PSM接收端检测复杂的问题,文献[15]提出了一种高效的接收天线组合选择方案,其利用信道矩阵的Wishart分布特征来选择接收天线组合,从而更好地提升了系统性能,并大大降低了系统复杂度。文献[16]则提出一种快速贪婪增量算法来进行接收天线组的选择,在显著降低系统复杂度的同时,增大了天线选择增益。为了对GPSM方案进一步拓展,文献[17]提出了一种广义预编码正交空间调制(generalized precoding-aided orthogonal spatial modulation,GPQSM)方案,其将传统QSM思想扩展到接收端,利用接收信号的同相和正交分量传送额外的信息比特,从而相较于典型GPSM系统可进一步提高系统频谱效率。

目前学术界对调制星座优化问题的研究也越来越广泛[18-19]。文献[20]中提出了一种双空间调制(double spatial modulation,DSM)技术。在每个时隙,DSM会在发射端进行两次独立的SM过程,且通过星座点的最优角度旋转来区分这两次SM过程,其可显著提高系统频谱效率和传输可靠性。文献[21-22]提出了一种信号空间分集(signal space diversity,SSD)方案,其通过将调制信号的相位进行旋转,使每次输入的比特流都由复信号的同相分量和正交分量来表示。所产生的两部分信号将随着时间推移交替发送,以实现分集增益并提高系统性能。文献[23]中提出一种多主动式天线的SM(multiple active antennas SM,MA-SM)方案,其在每个信道使用一种天线组合传输多个信号,以提高频谱效率,并与一个新的三维星座结合,在发射前对给定天线组合所发射的信号进行最优角度旋转,显著提高了系统性能。

在上述方案中,所有发射天线都被激活并发送预编码信息,而所有接收天线亦被用于实现数据映射。文献[24]提出了一种基于K个发射天线组的GPSM方案,同时利用发送天线和接收天线实现数据映射。在发送端,通过比特选择激活的发送天线组合,同时在接收端,通过迭代贪婪算法,对接收天线组合进行选择,大大降低了系统复杂度,显著提升了系统性能。文献[25-26]中提出了一种新的联合收发空间调制(joint transceiver spatial modulation,JSM)技术,其利用发送天线组合和一些冗余接收天线同时实现发送分集和接收分集。具体而言,该方案同时利用发送天线组合索引和接收天线索引来传递对应信息位,从而比仅在发射端或仅在接收端采用SM的方案获得更高传输速率,并通过采用冗余接收天线提高了系统可靠性。文献[27]则将QSM技术应用于JSM系统,提出了一种正交联合收发空间调制(orthogonal joint transceiver spatial modulation,QJSM)技术,其充分发挥了两者优势,可在发射端分别发送调制符号的同相分量和正交分量来扩展空间维度。因此,在理想情况下,QJSM的空间域频谱效率是传统JSM技术的两倍。此外,在QJSM方案中,JSM符号的实部和虚部在发射端通过正交载波独立发射,不存在信道间干扰影响,这也使QJSM系统可靠性得到显著提升。

基于上述研究分析,并受其启发,本文在JSM方案的基础上加入了最优角度旋转,从而极大地提升了系统频谱效率和传输可靠性。本文主要贡献如下:

(1) 提出了一种双联合收发空间调制(double joint transceiver spatial modulation,DJSM)方案,并对其通信过程及原理进行了详细阐述。所提DJSM方案在发送端进行两次独立的SM过程,可显著提升系统频谱效率。

(2) 为区分两次SM过程,对其中一次SM中的调制符号进行最优角度旋转,即第1个调制符号由第1组选择天线直接发送,而第2个调制符号则先进行角度旋转,然后由第2组激活天线发送。对于最优角度的选取,给出了对应的原理分析与仿真验证。

(3) 分析推导了DJSM系统的平均比特错误概率(average bit error probability,ABEP)性能,并对系统ABEP性能进行了蒙特卡罗仿真。同时对DJSM方案的复杂度进行了分析。仿真结果表明,在相同频谱效率下,DJSM方案与传统JSM方案以及其他较新的方案相比具有明显的性能优势。

1 系统模型

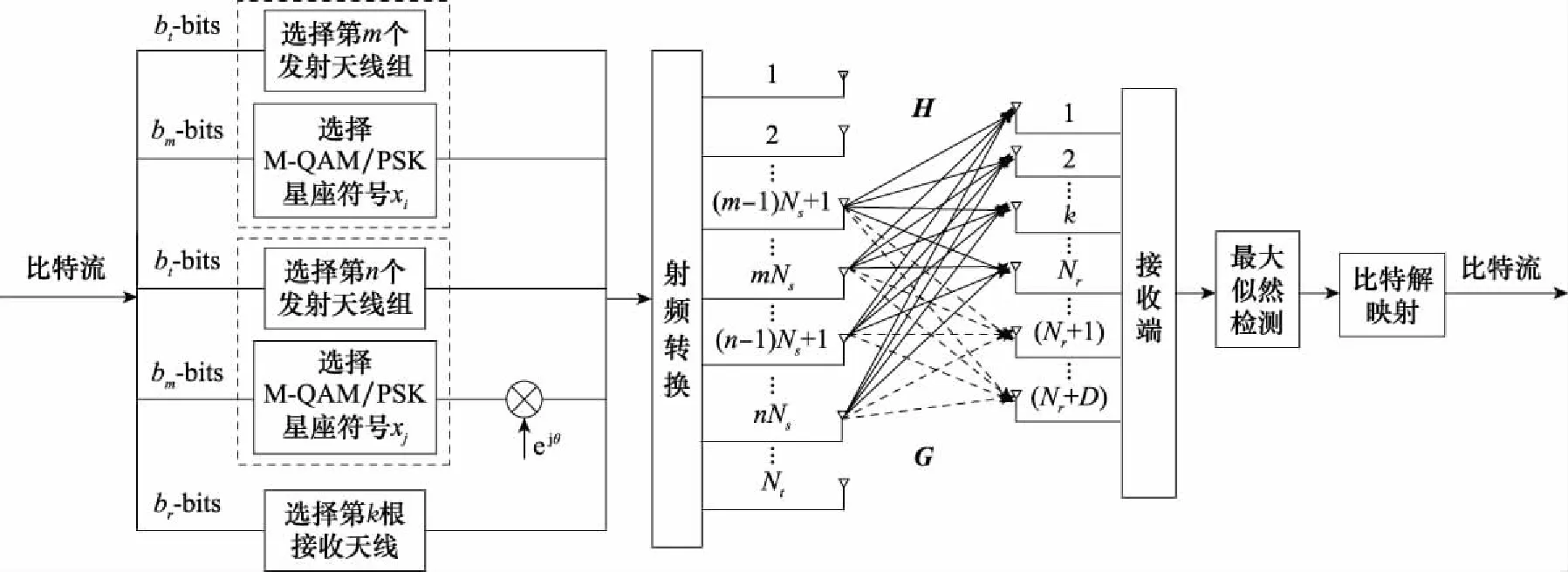
图1 DJSM系统模型Fig.1 System model of DJSM

(1)

输入信息比特可分成3个部分:第一部分为2bt个比特并平均分成两组,分别用来选择激活的发送天线分组m,m∈{1,2,…,2bt}和另一组激活的发送天线分组n,n∈{1,2,…,2bt};第二部分为2bm个比特,同样被平均分成两组,分别用来选择同两个激活分组所对应的两个调制符号xi,i∈{1,2,…,2bm}和xj,j∈{1,2,…,2bm};最后一部分为br个比特,用来从Nr根接收天线中选择第k根进行信息的接收。然后,符号xi直接由第m个发送天线分组发送,而符号xj先进行最优角度的旋转,然后由第n个发送天线分组发送。

因此,DJSM发送端的发送信号矢量可以表示为

x=Pmekxi+Pnekxjejθ

(2)

如系统采用迫零(zero-forcing,ZF)预编码,则预编码矩阵P可写成

P=ηHH(HHH)-1

(3)

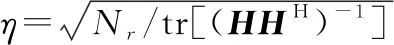
经过信道传输,在接收端接收到的信号可表示为

y1=HmPmekxi+HnPnekxjejθ+n1

(4)

y2=GmPmekxi+GnPnekxjejθ+n2

(5)

式中：y1∈CNr×1,y2∈CD×1分别表示在接收端的空间天线和分集天线处接收到的信号;n1∈CNr×1,n2∈CD×1是均值为0,方差为σ2的加性白高斯噪声(additive white Gaussian noise,AWGN)。

将式(4)与式(5)结合,可以得到接收端的接收信号为

y=WmPmekxi+WnPnekxjejθ+n

(6)

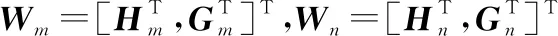
在接收端,通过对接收信号进行最大似然(maximum likelihood,ML)检测可以得到

(7)

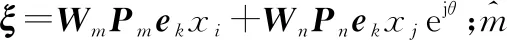
2 性能分析

在本节中,我们分析了DJSM系统的ABEP,给出了DJSM系统的上界性能。在以下的分析中,我们假设信道是独立的平坦瑞利衰落信道,且在每个时隙内信道保持不变。因此,利用联合上界技术,可得到DJSM方案的ABEP为

(8)

(9)

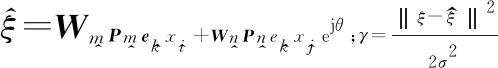
将式(9)代入式(8),则可以得到DJSM方案的ABEP为

(10)

表1 复杂度比较

由上述复杂度分析可知,本文所提DJSM方案的复杂度会略高于传统JSM方案的复杂度,其实时性也会有所降低。但从系统性能方面的分析可知本文所提DJSM方案的ABEP性能要显著优于传统的JSM方案。

3 最优角度选取

对于最优旋转角度的选取,其依据是使星座图中星座点间最小欧式距离最大化[30-32],即让DJSM方案中旋转之后的星座点与原星座点间的最小距离最大化来得到最优旋转角,表示为

(11)

式中：χ表示星座调制符号集。

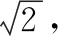
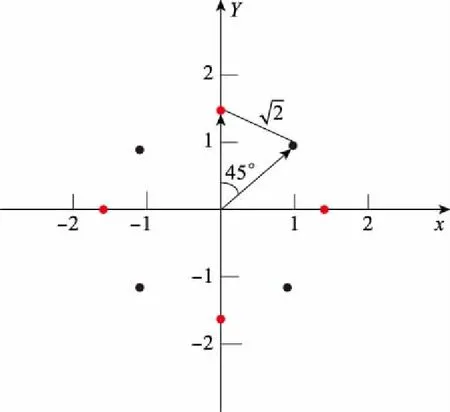
图2 4-QAM调制Fig.2 4-QAM modulation

图3是以最小化ABEP为目标,对不同调制方式下最优旋转角的选取进行了仿真。如图3所示,调制方式为BPSK、4-QAM及8-QAM。当BPSK及4-QAM调制的信噪比为14 dB,8-QAM调制的信噪比为20 dB时,BPSK,4-QAM,8-QAM星座的最佳旋转角分别为90°、45°和60°。

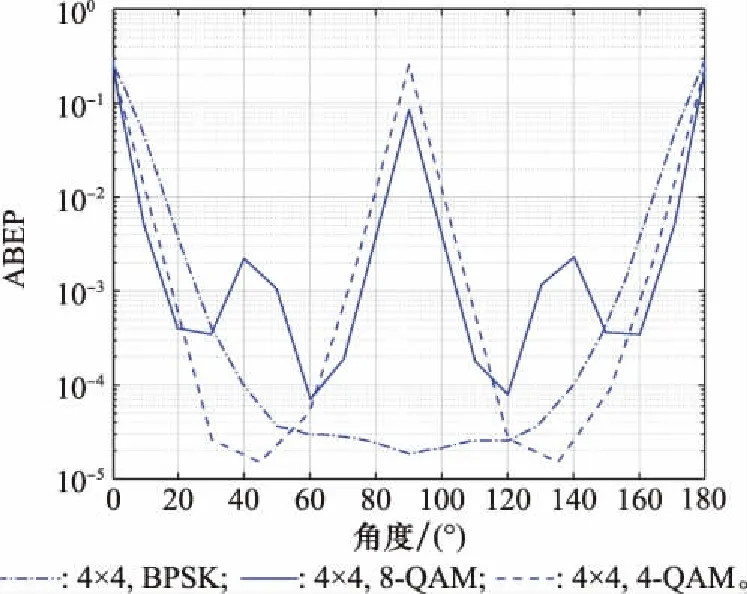
图3 旋转角度对ABEP的影响Fig.3 Influence of rotation angle on ABEP

4 仿真与结果分析

我们对所提出的DJSM方案进行了蒙特卡罗仿真。这里信道服从独立同分布的平坦瑞利衰落。当仿真中M=2时,系统采用的是BPSK调制;当M>2时,采用的是M -QAM调制。在相同频谱效率及不同系统参数下,我们对DJSM方案进行了程序仿真,并将DJSM方案与传统JSM方案以及文献[15]中提出的QJSM方案进行了仿真比较。

图4是在Nt=16、Ns=8、M=4、Nr=4的情况下,对DJSM方案在不同的分集天线数D下进行的性能仿真。由式(1)可知,当分集天线分别为D=1、D=2、D=4时,频谱效率同为8 bit/(s·Hz-1)。由图4可以看出,随着D的增加,系统的性能得到了提升,特别是在高信噪比下,性能增加更加明显。当ABEP=10-3时,D=4要比D=2和D=1分别获得约3.0 dB和10.0 dB的信噪比增益。这是因为随着分集天线D的增加,接收分集增益得到了提高,因此系统ABEP性能得到显著提升。

图4 DJSM方案在不同分集天线D下的ABEP性能(Nt=16, Ns=8, M=4, Nr=4)Fig.4 ABEP performance of DJSM scheme under different diversity antenna D (Nt=16,Ns=8, M=4, Nr=4)

图5是在Nt=16、Nr=2、D=4、M=4的条件下,对DJSM方案在不同发送天线数Ns下进行的性能仿真。这里设发射天线分组数量分别为8、4、2;且每组中发射天线数分别为2、4、8,其对应的系统频谱效率分别为11 bit/(s·Hz-1),9 bit/(s·Hz-1)及7 bit/(s·Hz-1)。

图5 DJSM方案在不同发送天线Ns下的ABEP性能(Nt=16, Nr=2, D=4, M=4)Fig.5 ABEP performance of DJSM scheme under different transmit antenna Ns (Nt=16, Nr=2, D=4, M=4)

从图5可以看出,随着Ns的增加,系统ABEP性能逐渐提升。当Ns=8时,其性能最好。这是因为当Nt=16时,随着Ns的增加,系统发送分集增大,且当Ns=8时,发送端发射天线分组的数量为2,其所携带的空间信息少,因此在D、Nr和M保持不变时,信息在接收端检测正确的可能性更大,从而使系统性能得到提升。

图6是在Nt=8,Ns=4,Nr=2,D=4时通过改变调制阶数M证明其对DJSM方案性能的影响。这里设置M=2、4和8,其对应系统频谱效率分别为5 bit/(s·Hz-1),7 bit/(s·Hz-1)和9 bit/(s·Hz-1)。

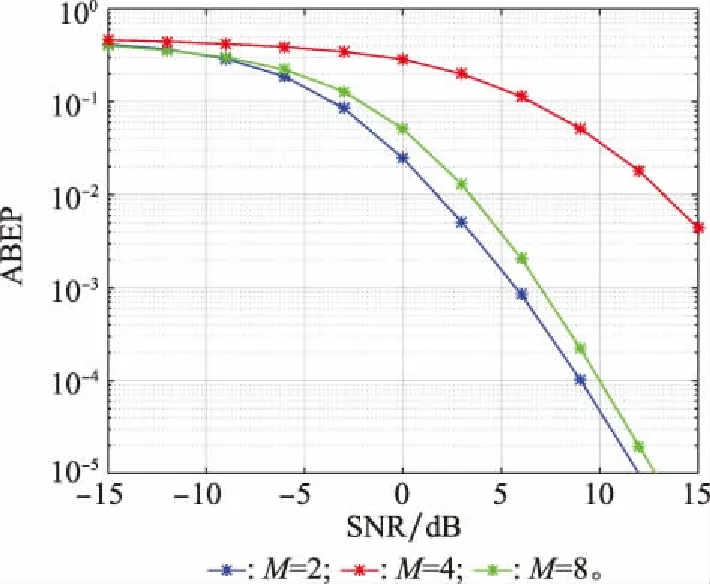
图6 DJSM方案在不同调制阶数M下的ABEP性能(Nt=8, Ns=4, Nr=2, D=4)Fig.6 ABEP performance of DJSM scheme under different modulation order M (Nt=8, Ns=4, Nr=2, D=4)

由图6可知,随着M的增大,系统ABEP性能逐渐变差,且当M=2和M=4时,其性能近似相同,而当M=8时,其性能与M=2和M=4时性能差距较大。这是因为当调制阶数较低时,调制符号所传输的信息相对较少,DJSM的检测错误主要由天线索引检测引起。因此,当调制阶数较低时,DJSM方案的性能变化不大,但随着调制阶数的增加,调制符号检测错误的可能性增加,从而造成较大的性能差距。

图7是在Nt=8、Ns=4、Nr=4、D=4且保持频谱效率均为8 bit/(s·Hz-1)的情况下,针对不同调制阶数M,DJSM方案同传统JSM方案以及DSM方案的ABEP性能比较。

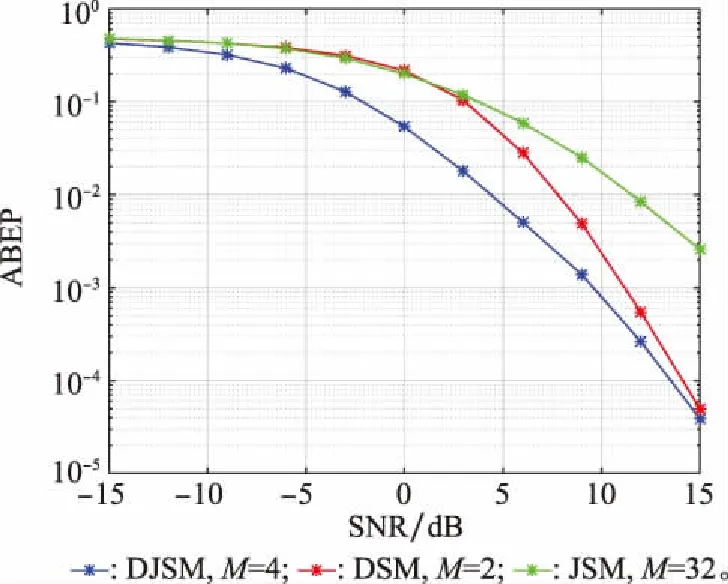
图7 DJSM,JSM,DSM方案的ABEP性能比较(Nt=8, Ns=4, Nr=4, D=8)Fig.7 ABEP performance comparison of DJSM, JSM and DSM schemes (Nt=8, Ns=4, Nr=4, D=8)

由图7可以看出,DJSM方案的性能要优于JSM方案以及DSM方案。当ABEP=10-2时,DJSM较JSM约有8.0 dB的信噪比增益,即在相同频谱效率下,DJSM方案所需调制的阶数远低于JSM,从而可使信号星座点间最小欧式距离变大,使错误率下降。此时,DJSM较DSM大约有4.0 dB的信噪比增益,这是因为DJSM方案在发送端是激活一个发送天线组进行信息传输,并且在接收端采用额外的接收天线接收信号,因此具有较高的发送分集增益和接收分集增益,可使系统性能更优。由图7仿真结果可以看出本文所提DJSM方案的性能优势,但其复杂度也会有一定的增加,这相当于以较低复杂代价来换取较大的性能增益。

当Nt=8、Nr=4,且频谱效率为8 bit/(s·Hz-1)时,不同调制阶数下,DJSM方案同GPQSM、QJSM及GSM方案的性能比较如图8所示。

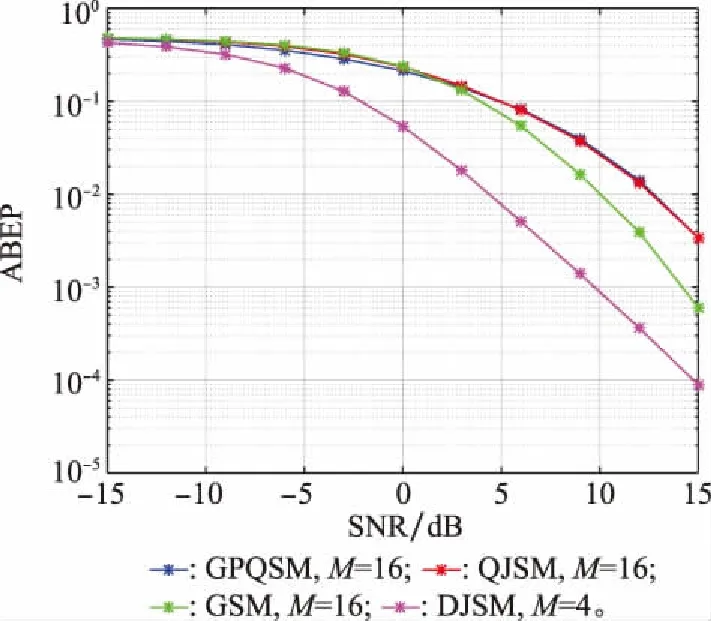
图8 不同方案的ABEP性能比较Fig.8 ABEP performance comparison of different schemes

对DJSM方案和QJSM方案有Ns=4,D=8;对GSM方案,其发送端选择两根天线传送信息;对GPQSM方案,则在接收端选择两根天线接收信息。从图8可以看出,在所给信噪比范围内,本文所提DJSM方案在相同频谱效率下的性能均优于其他几种方案。当ABEP=10-2时,DJSM方案较GSM、QJSM以及GPQSM方案分别约有6.0 dB、8.5 dB及8.5 dB的信噪比增益。因此DJSM方案在相同频谱效率下,可较上述SM方案获得明显的ABEP性能优势。

5 结 论

本文提出一种DJSM方案,其在发送端进行两次独立的SM过程,并利用星座旋转叠加空间传输矢量,最后联合选择发送天线分组索引、接收天线索引以及调制符号,实现了发送分集增益、接收分集增益以及复用增益,显著提升了系统频谱效率和可靠性。本文推导给出DJSM方案的ABEP理论表示,并分析了最优旋转角度的选取。仿真结果表明DJSM方案性能明显优于传统JSM及QJSM方案,但其复杂度也有一定增加,未来我们将进一步研究低复杂度DJSM方案。